Física Quântica

“Acho que é seguro dizer que ninguém entende quântico mecânica. ” —Físico Richard P. Feynman

Dizer que a invenção de dispositivos semicondutores foi uma revolução não seria exagero. Isso não foi apenas uma conquista tecnológica impressionante, mas também abriu o caminho para desenvolvimentos que alterariam indelevelmente a sociedade moderna. Dispositivos semicondutores tornaram possível a eletrônica miniaturizada, incluindo computadores, certos tipos de equipamentos médicos de diagnóstico e tratamento e dispositivos de telecomunicações populares, para citar algumas aplicações dessa tecnologia.

Por trás dessa revolução na tecnologia está uma revolução ainda maior na ciência geral:o campo da física quântica . Sem esse salto na compreensão do mundo natural, o desenvolvimento de dispositivos semicondutores (e dispositivos eletrônicos mais avançados ainda em desenvolvimento) nunca teria sido possível. A física quântica é um domínio da ciência incrivelmente complicado. Este capítulo é apenas uma breve visão geral. Quando cientistas do calibre de Feynman dizem que "ninguém entende [isso]", você pode ter certeza que é um assunto complexo. Sem uma compreensão básica da física quântica, ou pelo menos uma compreensão das descobertas científicas que levaram à sua formulação, no entanto, é impossível entender como e por que os dispositivos eletrônicos semicondutores funcionam. A maioria dos livros introdutórios de eletrônica que li tenta explicar os semicondutores em termos da física "clássica", resultando em mais confusão do que compreensão.

Atom

Muitos de nós já vimos diagramas de átomos que se parecem com a figura abaixo.



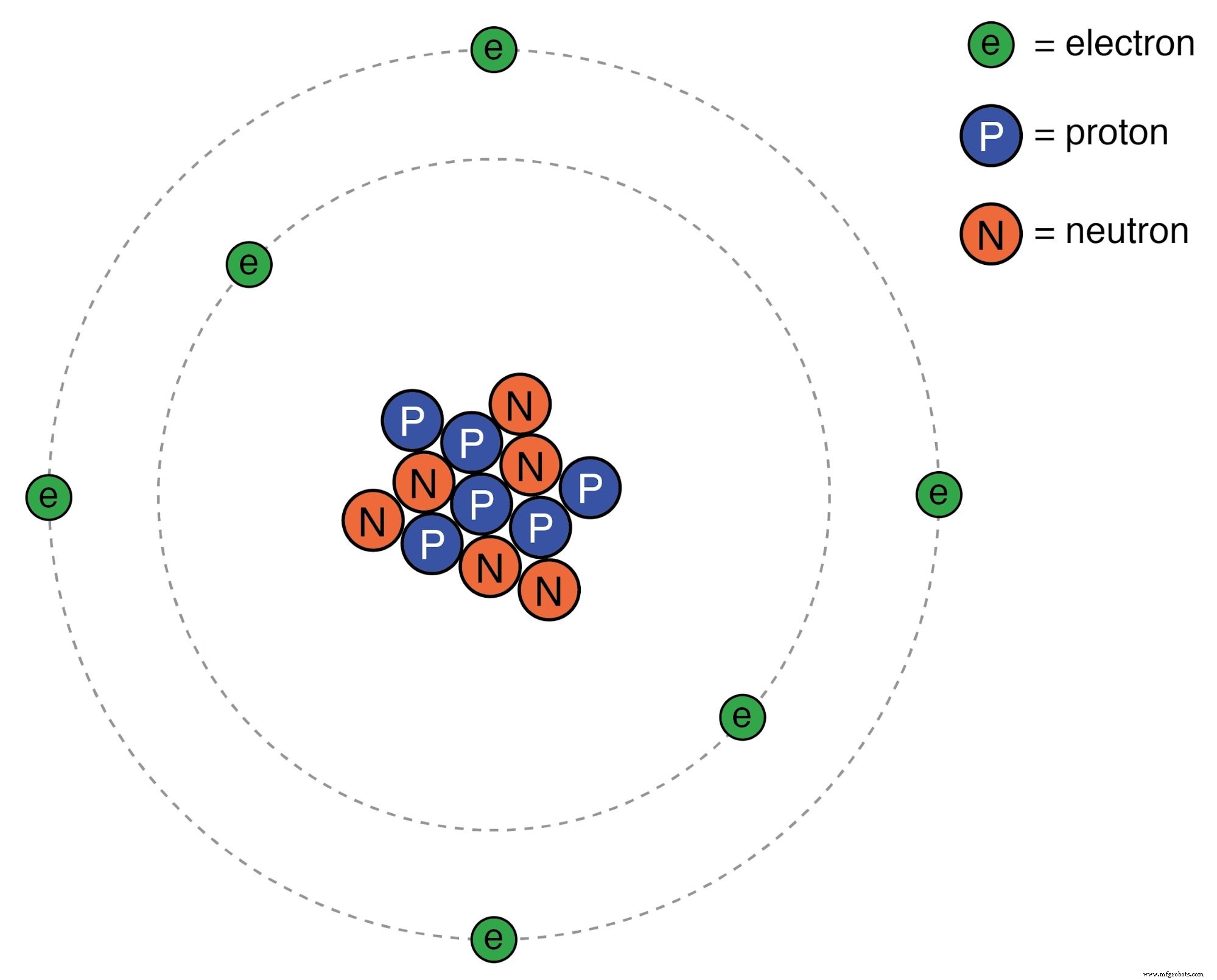
Átomo de Rutherford:elétrons negativos orbitam um pequeno núcleo positivo.

Minúsculas partículas de matéria chamadas prótons e nêutrons constituem o centro do átomo; elétrons orbita como planetas ao redor de uma estrela. O núcleo carrega uma carga elétrica positiva, devido à presença de prótons (os nêutrons não têm nenhuma carga elétrica), enquanto a carga negativa de equilíbrio do átomo reside nos elétrons em órbita. Os elétrons negativos são atraídos pelos prótons positivos, assim como os planetas são atraídos gravitacionalmente pelo Sol, mas as órbitas são estáveis ​​por causa do movimento dos elétrons. Devemos este modelo popular do átomo ao trabalho de Ernest Rutherford, que por volta do ano de 1911 determinou experimentalmente que as cargas positivas dos átomos estavam concentradas em um núcleo denso e minúsculo, em vez de se espalharem uniformemente sobre o diâmetro, conforme proposto por um pesquisador anterior , JJ Thompson.

Dispersão de Rutherford

O experimento de espalhamento de Rutherford envolve o bombardeio de uma folha de ouro fina com partículas alfa carregadas positivamente, como na Figura abaixo. Os jovens estudantes de pós-graduação H. Geiger e E. Marsden tiveram resultados inesperados. Algumas partículas Alpha foram desviadas em grandes ângulos. Algumas partículas Alfa se espalharam, recuando a quase 180 ^o . A maioria das partículas passou pela folha de ouro sem ser refletida, indicando que a folha era quase todo um espaço vazio. O fato de que algumas partículas alfa experimentaram grandes deflexões indicava a presença de um minúsculo núcleo carregado positivamente.



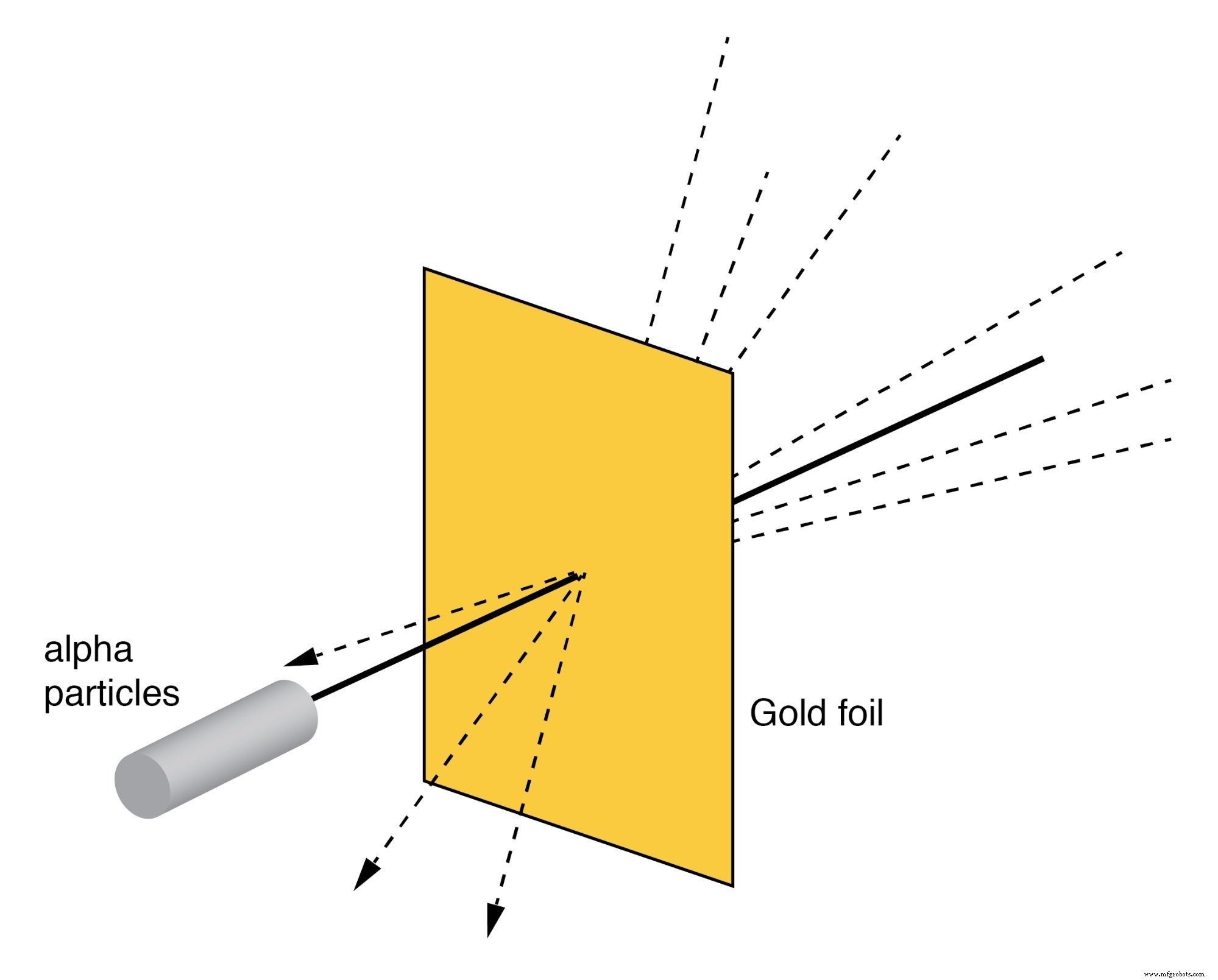
Espalhamento de Rutherford:um feixe de partículas alfa é espalhado por uma fina folha de ouro.

Embora o modelo atômico de Rutherford representasse os dados experimentais melhor do que o de Thompson, ainda não era perfeito. Outras tentativas de definir a estrutura atômica foram realizadas, e esses esforços ajudaram a pavimentar o caminho para as descobertas bizarras da física quântica. Hoje, nossa compreensão do átomo é um pouco mais complexa. No entanto, apesar da revolução da física quântica e sua contribuição para a nossa compreensão da estrutura atômica, a imagem do átomo do sistema solar de Rutherford se incorporou à consciência popular a tal ponto que persiste em algumas áreas de estudo, mesmo quando inadequada.

Considere esta breve descrição dos elétrons em um átomo, tirada de um livro popular de eletrônica:

Os elétrons negativos em órbita são, portanto, atraídos para o núcleo positivo, o que nos leva à questão de por que os elétrons não voam para o núcleo do átomo. A resposta é que os elétrons em órbita permanecem em sua órbita estável por causa de duas forças iguais, mas opostas. A força centrífuga para fora exercida sobre os elétrons por causa da órbita neutraliza a força atrativa para dentro (centrípeta) tentando puxar os elétrons em direção ao núcleo por causa das cargas diferentes.

Seguindo o modelo de Rutherford, este autor projeta os elétrons como pedaços sólidos de matéria envolvidos em órbitas circulares, sua atração interna para o núcleo com carga oposta equilibrada por seu movimento. A referência à "força centrífuga" é tecnicamente incorreta (mesmo para planetas em órbita), mas é facilmente perdoada por causa de sua aceitação popular:na realidade, não existe força empurrando qualquer corpo orbital afastado de seu centro de órbita. Parece que sim porque a inércia de um corpo tende a mantê-lo viajando em linha reta, e uma vez que uma órbita é um desvio constante (aceleração) da viagem em linha reta, há uma oposição inercial constante a qualquer força que esteja atraindo o corpo em direção à órbita centro (centrípeto), seja gravidade, atração eletrostática ou mesmo a tensão de um elo mecânico.

O verdadeiro problema com essa explicação, entretanto, é a ideia de elétrons viajando em órbitas circulares em primeiro lugar. É um fato verificável que cargas elétricas em aceleração emitem radiação eletromagnética, e esse fato era conhecido mesmo na época de Rutherford. Uma vez que o movimento orbital é uma forma de aceleração (o objeto orbital em aceleração constante longe do movimento normal em linha reta), os elétrons em um estado orbital deveriam estar emitindo radiação como lama de um pneu girando. Elétrons acelerados em torno de caminhos circulares em aceleradores de partículas chamados síncrotrons são conhecidos por fazer isso, e o resultado é chamado de radiação síncrotron . Se os elétrons estivessem perdendo energia dessa maneira, suas órbitas acabariam decaindo, resultando em colisões com o núcleo carregado positivamente. No entanto, isso normalmente não acontece dentro dos átomos. Na verdade, as “órbitas” de elétrons são notavelmente estáveis ​​em uma ampla gama de condições.

Átomos Excitados

Além disso, experimentos com átomos “excitados” demonstraram que a energia eletromagnética emitida por um átomo ocorre apenas em certas frequências definidas. Os átomos que são "excitados" por influências externas, como a luz, são conhecidos por absorver essa energia e devolvê-la como ondas eletromagnéticas de frequências específicas, como um diapasão que toca em um tom fixo, não importa como é atingido. Quando a luz emitida por um átomo excitado é dividida em suas frequências constituintes (cores) por um prisma, linhas distintas de cor aparecem no espectro, o padrão das linhas espectrais sendo exclusivo para aquele elemento. Esse fenômeno é comumente usado para identificar elementos atômicos e até mesmo medir as proporções de cada elemento em um composto ou mistura química. De acordo com o modelo atômico do sistema solar de Rutherford (considerando os elétrons como pedaços de matéria livres para orbitar em qualquer raio) e as leis da física clássica, os átomos excitados devem retornar energia em uma faixa virtualmente ilimitada de frequências, em vez de alguns poucos selecionados. Em outras palavras, se o modelo de Rutherford estivesse correto, não haveria efeito de "diapasão" e o espectro de luz emitido por qualquer átomo apareceria como uma faixa contínua de cores, em vez de algumas linhas distintas.

BohrModel

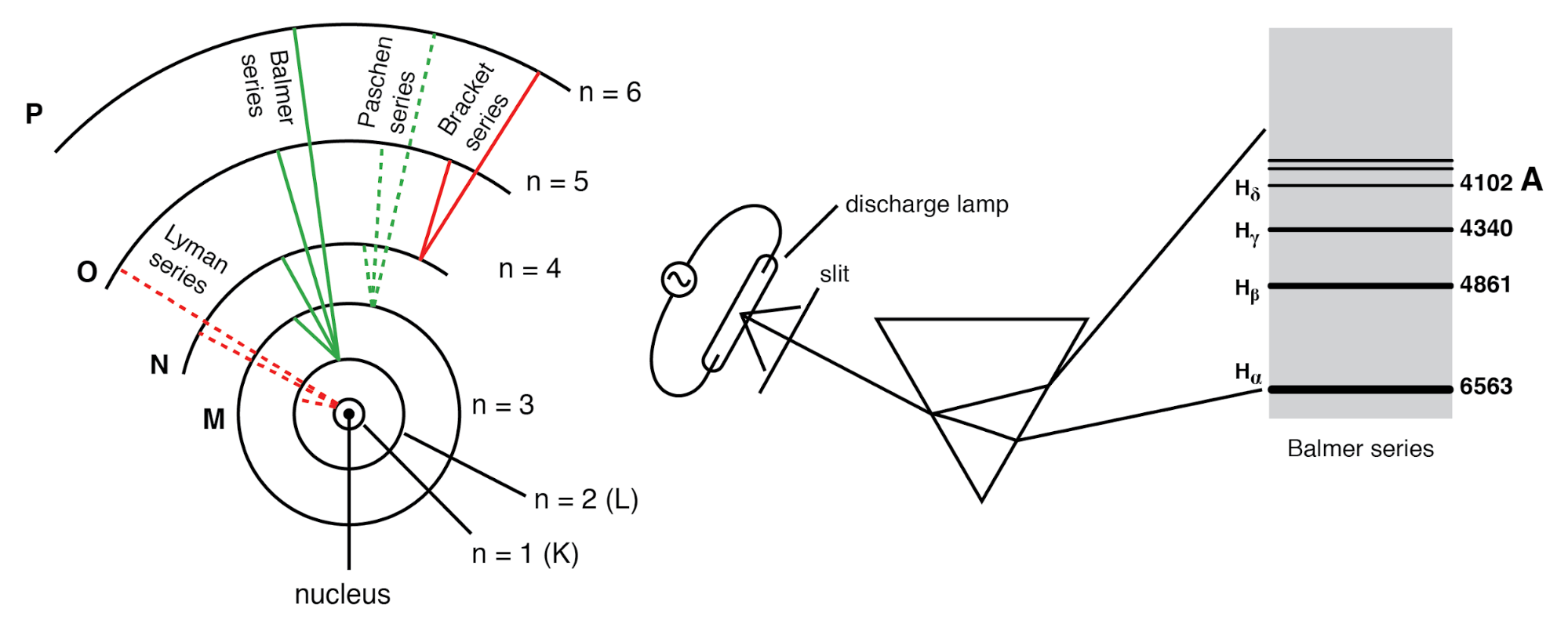
O átomo de hidrogênio de Bohr (com órbitas desenhadas em escala) só permite que os elétrons habitem orbitais discretos. Os elétrons caindo de n =3,4,5 ou 6 para n =2 são responsáveis ​​pela série de linhas espectrais de Balmer.

Um pesquisador pioneiro chamado Niels Bohr tentou melhorar o modelo de Rutherford depois de estudar no laboratório de Rutherford por vários meses em 1912. Tentando harmonizar as descobertas de outros físicos (principalmente, Max Planck e Albert Einstein), Bohr sugeriu que cada elétron tinha uma certa quantidade específica de energia, e que suas órbitas eram quantizadas de modo que cada um pode ocupar certos lugares ao redor do núcleo, como bolas de gude fixadas em trilhas circulares ao redor do núcleo, em vez dos satélites de alcance livre que cada um era anteriormente imaginado ser. (Figura acima) Em deferência às leis do eletromagnético e das cargas de aceleração, Bohr aludiu a essas "órbitas" como estados estacionários para escapar da implicação de que eles estavam em movimento. Embora a ambiciosa tentativa de Bohr de reenquadrar a estrutura do átomo em termos mais próximos dos resultados experimentais tenha sido um marco na física, não foi concluída. Sua análise matemática produziu melhores previsões de eventos experimentais do que análises pertencentes a modelos anteriores, mas ainda havia algumas perguntas sem resposta sobre por quê os elétrons deveriam se comportar de maneiras estranhas. A afirmação de que os elétrons existiam em estados estacionários e quantizados ao redor do núcleo explicava os dados experimentais melhor do que o modelo de Rutherford, mas ele não tinha ideia do que forçaria os elétrons a manifestar esses estados particulares. A resposta a essa pergunta teve que vir de outro físico, Louis de Broglie, cerca de uma década depois.

Hipótese De Broglie

De Broglie propôs que os elétrons, como fótons (partículas de luz), manifestam propriedades tanto de partícula quanto de onda. Com base nessa proposta, ele sugeriu que uma análise dos elétrons em órbita a partir de uma perspectiva de onda, em vez de uma perspectiva de partícula, pode dar mais sentido à sua natureza quantizada. Na verdade, outro avanço no entendimento foi alcançado.



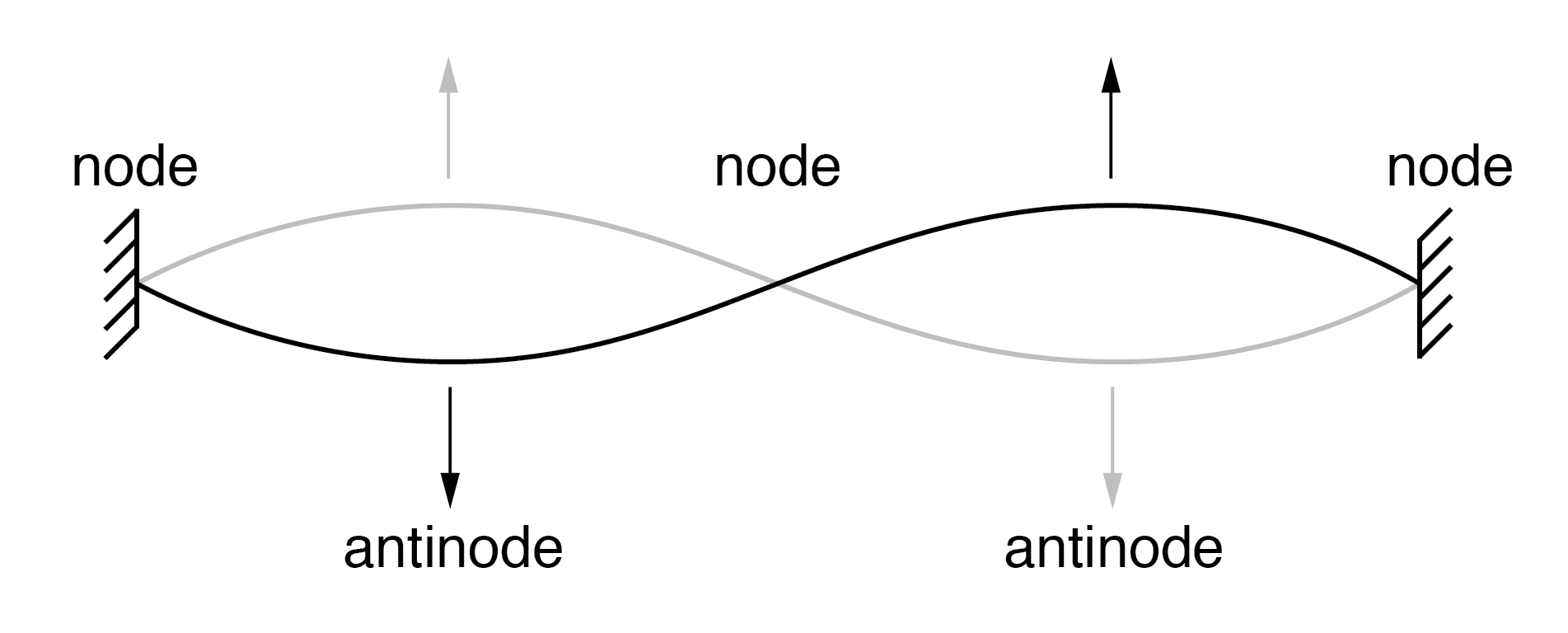
Corda vibrando em frequência ressonante entre dois pontos fixos forma onda estacionária .

O átomo de acordo com de Broglie consistia em elétrons existindo como ondas estacionárias , um fenômeno bem conhecido pelos físicos em uma variedade de formas. Como a corda dedilhada de um instrumento musical (Figura acima) vibrando em uma frequência ressonante, com “nós” e “antinodos” em posições estáveis ​​ao longo de seu comprimento. De Broglie imaginou elétrons ao redor dos átomos formando ondas que se curvavam ao redor de um círculo, como na figura abaixo.



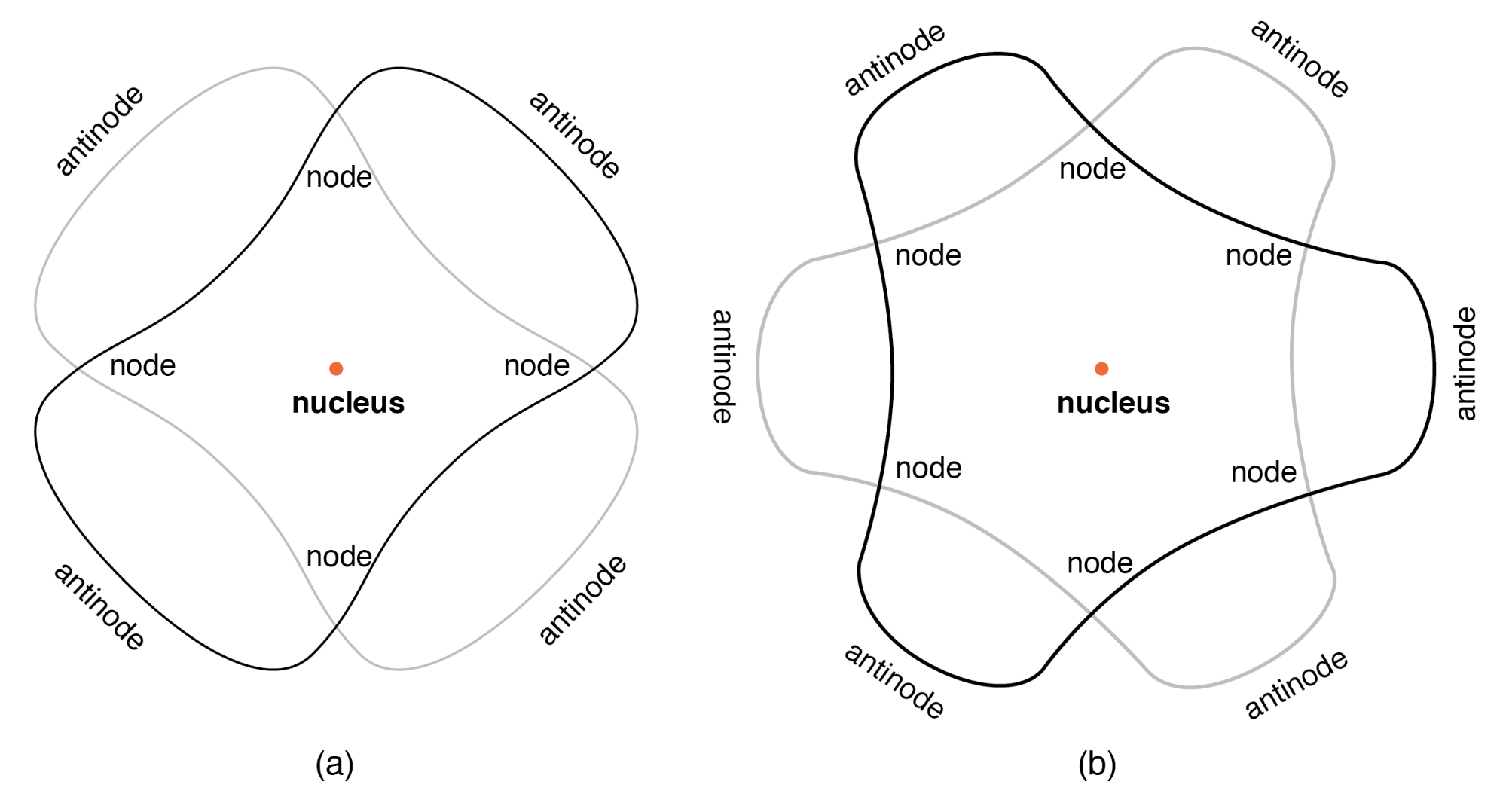
“Orbitando” elétron como uma onda estacionária ao redor do núcleo, (a) dois ciclos por órbita, (b) três ciclos por órbita.

Os elétrons só podiam existir em “órbitas” certas e definidas ao redor do núcleo porque essas eram as únicas distâncias em que as extremidades da onda coincidiam. Em qualquer outro raio, a onda deve interferir destrutivamente em si mesma e, portanto, deixar de existir. A hipótese de De Broglie deu suporte matemático e uma analogia física conveniente para explicar os estados quantizados dos elétrons dentro de um átomo, mas seu modelo atômico ainda estava incompleto. Dentro de alguns anos, porém, os físicos Werner Heisenberg e Erwin Schrodinger, trabalhando independentemente um do outro, construíram o conceito de de Broglie de uma dualidade de onda de matéria para criar modelos matematicamente mais rigorosos de partículas subatômicas.

Mecânica Quântica

Este avanço teórico do modelo de onda estacionária primitiva de de Broglie para a matriz de Heisenberg e os modelos de equação diferencial de Schrodinger recebeu o nome de mecânica quântica e introduziu uma característica bastante chocante ao mundo das partículas subatômicas:o traço da probabilidade, ou incerteza. De acordo com a nova teoria quântica, era impossível determinar a posição exata e momento exato de uma partícula ao mesmo tempo. A explicação popular deste "princípio de incerteza" era que era um erro de medição (ou seja, ao tentar medir com precisão a posição de um elétron, você interfere em seu momento e, portanto, não pode saber o que era antes de a medição de posição ser feita, e vice-versa versa). A implicação surpreendente da mecânica quântica é que as partículas não têm posições precisas e momentos, mas sim equilibrar as duas quantidades de tal forma que suas incertezas combinadas nunca diminuam abaixo de um certo valor mínimo.

Esta forma de relação de “incerteza” existe em outras áreas além da mecânica quântica. Conforme discutido no capítulo "Sinais CA de Frequência Mista" no volume II desta série de livros, há uma relação mutuamente exclusiva entre a certeza dos dados de domínio de tempo de uma forma de onda e seus dados de domínio de frequência. Em termos simples, quanto mais precisamente sabemos sua (s) frequência (s) constituinte (s), menos precisamente sabemos sua amplitude no tempo e vice-versa. Para me citar:

Uma forma de onda de duração infinita (número infinito de ciclos) pode ser analisada com precisão absoluta, mas quanto menos ciclos disponíveis para o computador para análise, menos precisa a análise. . . Quanto menos vezes o ciclo de uma onda, menos certa será sua frequência. Levando este conceito ao seu extremo lógico, um pulso curto - uma forma de onda que nem mesmo completa um ciclo - na verdade não tem frequência, mas age como uma gama infinita de frequências. Este princípio é comum a todos os fenômenos baseados em ondas, não apenas às tensões e correntes AC.

Para determinar com precisão a amplitude de um sinal variável, devemos amostrá-lo em um intervalo de tempo muito estreito. No entanto, fazer isso limita nossa visão da frequência da onda. Por outro lado, para determinar a frequência de uma onda com grande precisão, devemos amostrá-la ao longo de muitos ciclos, o que significa que perdemos a visão de sua amplitude a qualquer momento. Assim, não podemos saber simultaneamente a amplitude instantânea e a frequência geral de qualquer onda com precisão ilimitada. Mais estranho ainda, essa incerteza é muito mais do que imprecisão do observador; ele reside na própria natureza da onda. Não é como se fosse possível, com a tecnologia adequada, obter medições precisas de ambos amplitude e frequência instantâneas ao mesmo tempo. Literalmente, uma onda não pode ter uma amplitude precisa e instantânea e uma freqüência precisa ao mesmo tempo.

A incerteza mínima da posição e momento de uma partícula expressa por Heisenberg e Schrõdinger não tem nada a ver com limitação na medição; em vez disso, é uma propriedade intrínseca da natureza dual da onda de matéria da partícula. Os elétrons, portanto, não existem realmente em suas "órbitas" como pedaços de matéria precisamente definidos, ou mesmo como formas de ondas definidas com precisão, mas sim como "nuvens" - o termo técnico é função de onda - da distribuição de probabilidade, como se cada elétron fosse “espalhado” ou “espalhado” por uma gama de posições e momentos.

Essa visão radical dos elétrons como nuvens imprecisas à primeira vista parece contradizer o princípio original dos estados de elétrons quantizados:que os elétrons existem em “órbitas” distintas e definidas em torno dos núcleos atômicos. Afinal, foi essa descoberta que levou à formação da teoria quântica para explicá-la. Parece estranho que uma teoria desenvolvida para explicar o comportamento discreto dos elétrons acabe declarando que os elétrons existem como “nuvens” e não como pedaços discretos de matéria. No entanto, o comportamento quantizado dos elétrons não depende de eles terem posição e valores de momento definidos, mas sim de outras propriedades chamadas de números quânticos . Em essência, a mecânica quântica dispensa as noções comumente aceitas de posição absoluta e momento absoluto, e as substitui por noções absolutas de um tipo que não tem analogia na experiência comum.

Quatro Números Quânticos

Embora se saiba que os elétrons existem em formas etéreas, "semelhantes a nuvens" de probabilidade distribuída, em vez de como pedaços discretos de matéria, essas "nuvens" têm outras características que são discreto. Qualquer elétron em um átomo pode ser descrito por quatro medidas numéricas (os números quânticos mencionados anteriormente ), chamado de Diretor , Momento angular , Magnético , e girar números. A seguir está uma sinopse dos significados de cada um desses números:

1 Número quântico principal

Número Quantum Principal: Simbolizado pela letra n , este número descreve o shell em que um elétron reside. Uma "camada" de elétron é uma região do espaço em torno do núcleo de um átomo em que os elétrons podem existir, correspondendo aos padrões estáveis ​​de "onda estacionária" de de Broglie e Bohr. Os elétrons podem “pular” de camada em camada, mas não podem existir entre as regiões da casca. O número quântico principal deve ser um número inteiro positivo (um número inteiro, maior ou igual a 1). Em outras palavras, o número quântico principal para um elétron não pode ser 1/2 ou -3. Esses valores inteiros não foram obtidos arbitrariamente, mas sim por meio de evidências experimentais de espectros de luz:as diferentes frequências (cores) da luz emitida por átomos de hidrogênio excitados seguem uma sequência matematicamente dependente de valores inteiros específicos, conforme ilustrado na Figura anterior.

Cada camada tem a capacidade de conter vários elétrons. Uma analogia para as camadas de elétrons são as fileiras concêntricas de assentos de um anfiteatro. Assim como uma pessoa sentada em um anfiteatro deve escolher uma fileira para sentar (não se pode sentar entre fileiras), os elétrons devem “escolher” uma camada específica para se “sentar”. Como nas fileiras do anfiteatro, as camadas mais externas contêm mais elétrons do que as camadas internas. Além disso, os elétrons tendem a buscar a camada mais baixa disponível, enquanto as pessoas em um anfiteatro procuram o assento mais próximo do centro do palco. Quanto maior o número da camada, maior será a energia dos elétrons nela.

O número máximo de elétrons que qualquer camada pode conter é descrito pela equação 2n ² , onde “n” é o número quântico principal. Assim, a primeira camada (n =1) pode conter 2 elétrons; a segunda camada (n =2) 8 elétrons e a terceira camada (n =3) 18 elétrons. (Figura abaixo)



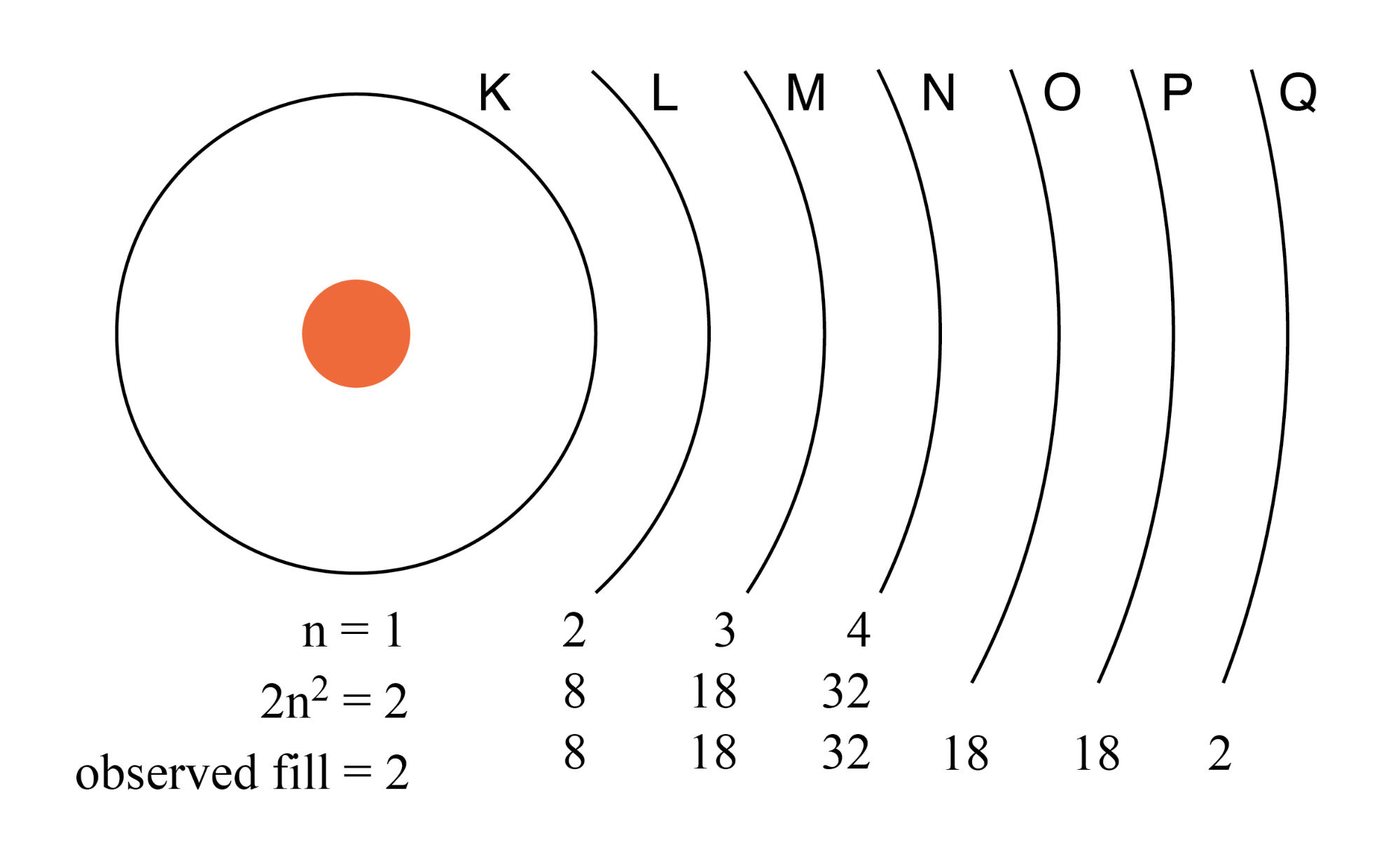
As camadas de elétrons em um átomo eram anteriormente designadas por letras em vez de números. A primeira camada (n =1) foi rotulada K, a segunda camada (n =2) L, a terceira camada (n =3) M, a quarta camada (n =4) N, a quinta camada (n =5) O, a sexta camada (n =6) P e a sétima camada (n =7) Q.

2. Número quântico do momento angular

Número quântico do momento angular: Uma concha é composta de subcamadas. Alguém pode estar inclinado a pensar em sub-camadas como simples subdivisões de conchas, como faixas que dividem uma estrada. Os subshells são muito mais estranhos. Subcamadas são regiões do espaço onde “nuvens” de elétrons podem existir, e diferentes subcamadas têm, na verdade, formatos diferentes. A primeira subcamada tem o formato de uma esfera (Figura abaixo (s)), o que faz sentido quando visualizada como uma nuvem de elétrons circundando o núcleo atômico em três dimensões. A segunda sub camada, no entanto, se assemelha a um haltere, composto por dois "lóbulos" unidos em um único ponto próximo ao centro do átomo. (Figura abaixo (p)) A terceira subcamada normalmente se assemelha a um conjunto de quatro "lóbulos" agrupados em torno do núcleo do átomo. Essas formas de subcamadas são uma reminiscência de representações gráficas da intensidade do sinal da antena de rádio, com regiões em forma de lóbulo bulboso que se estendem da antena em várias direções. (Figura abaixo (d))



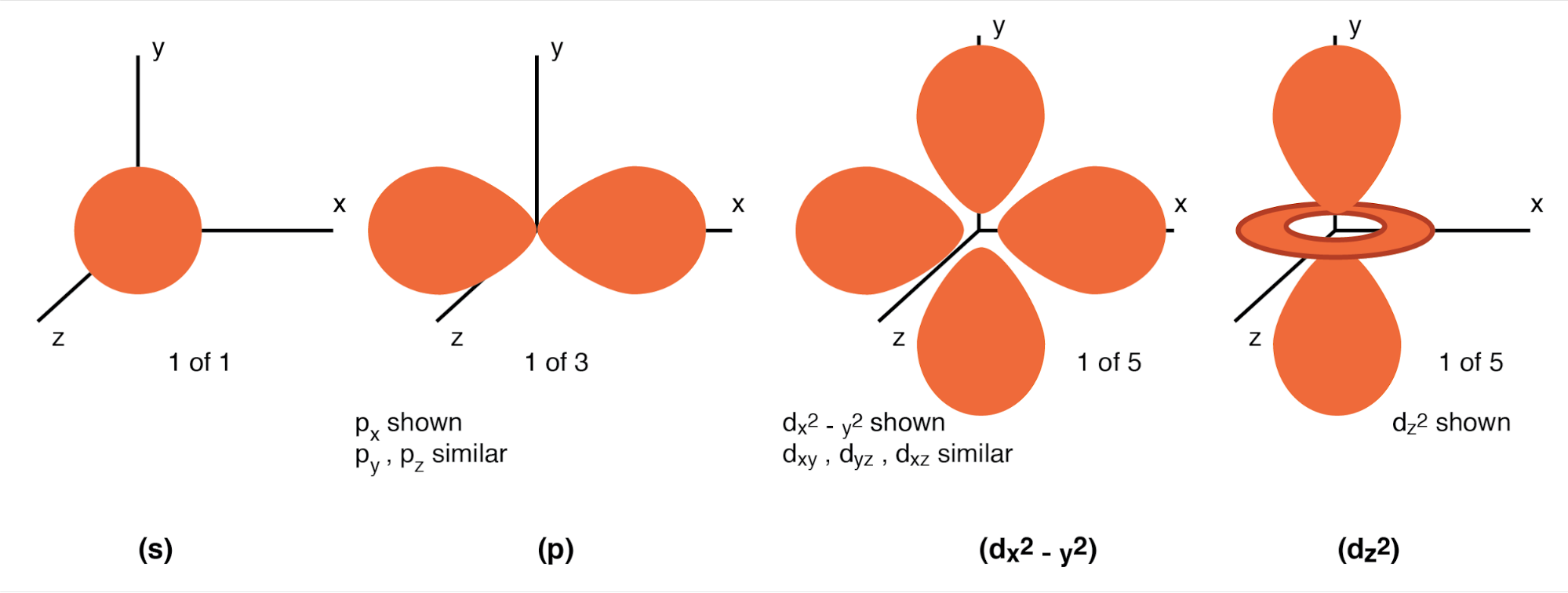
Os números quânticos de momento angular válidos são inteiros positivos como os números quânticos principais, mas também incluem zero. Esses números quânticos para elétrons são simbolizados pela letra l. O número de sub-camadas em uma camada é igual ao número quântico principal da camada. Assim, a primeira camada (n =1) possui uma sub camada, numerada 0; a segunda camada (n =2) tem duas sub camadas, numeradas 0 e 1; a terceira camada (n =3) tem três sub camadas, numeradas 0, 1 e 2.

Uma convenção mais antiga para a descrição do subshell usava letras em vez de números. Nesta notação, a primeira sub camada (l =0) foi designada s, a segunda sub camada (l =1) designada p, a terceira sub camada (l =2) designada d e a quarta sub camada (l =3) designada f. As letras vêm das palavras sustenido, principal (não deve ser confundido com o número quântico principal, n), difuso e fundamental. Você ainda verá essa convenção notacional em muitas tabelas periódicas, usadas para designar a configuração eletrônica das camadas mais externas ou de valência do átomo. (Figura abaixo)







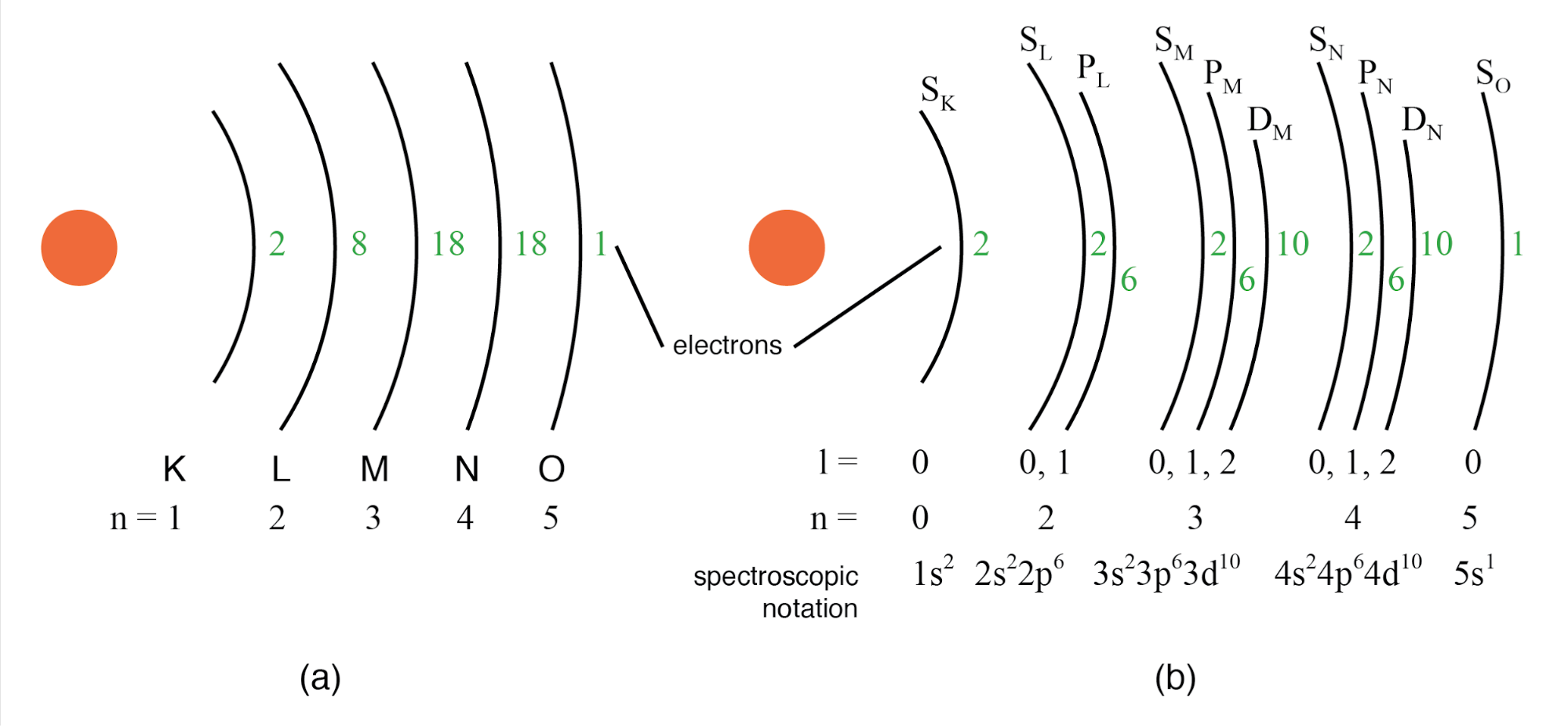
(a) Representação de Bohr do átomo de prata, (b) Representação de subcamada de Ag com divisão das camadas em subcamadas (número quântico angular l). Este diagrama não implica nada sobre a posição real dos elétrons, mas representa os níveis de energia.

3. Número quântico magnético

Número quântico magnético: O número quântico magnético para um elétron classifica a orientação de sua forma subcamada. Os “lóbulos” para subshells apontam em várias direções. Essas diferentes orientações são chamadas de orbitais . Para a primeira subcamada (s; l =0), que se assemelha a uma esfera apontando em nenhuma "direção", então há apenas um orbital. Para a segunda subcamada (p; l =1) em cada casca, que se assemelha a halteres apontam em três direções possíveis. Pense em três halteres se cruzando na origem, cada um orientado ao longo de um eixo diferente em um espaço de coordenadas de três eixos.

Os valores numéricos válidos para este número quântico consistem em inteiros variando de -l a l e são simbolizados como m _l em física atômica e l _z em física nuclear. Para calcular o número de orbitais em qualquer subcamada, dobre o número da subcamada e adicione 1, (2 · l + 1). Por exemplo, a primeira sub camada (l =0) em qualquer camada contém um único orbital, numerado 0; a segunda subcamada (l =1) em qualquer camada contém três orbitais, numerados -1, 0 e 1; a terceira subcamada (l =2) contém cinco orbitais, numerados -2, -1, 0, 1 e 2; e assim por diante.

Como os números quânticos principais, o número quântico magnético surgiu diretamente de evidências experimentais:o efeito Zeeman, a divisão de linhas espectrais pela exposição de um gás ionizado a um campo magnético, daí o nome número quântico “magnético”.

4. Número Spin Quantum

Número Spin Quantum: Como o número quântico magnético, essa propriedade dos elétrons atômicos foi descoberta por meio de experimentação. A observação atenta das linhas espectrais revelou que cada linha era na verdade um par de linhas muito próximas e esta chamada estrutura fina foi hipotetizado como resultado de cada elétron “girando” em um eixo como se fosse um planeta. Elétrons com diferentes “spins” emitiam frequências de luz ligeiramente diferentes quando excitados. O nome “spin” foi atribuído a este número quântico. O conceito de um elétron girando agora é obsoleto, sendo mais adequado para a visão (incorreta) dos elétrons como pedaços discretos de matéria em vez de “nuvens”; mas, o nome permanece.

Os números quânticos de spin são simbolizados como m _s em física atômica e s _z em física nuclear. Para cada orbital em cada subcamada em cada camada, pode haver dois elétrons, um com spin +1/2 e o outro com spin -1/2.

Princípio de exclusão de Pauli

O físico Wolfgang Pauli desenvolveu um princípio que explica a ordem dos elétrons em um átomo de acordo com esses números quânticos. Seu princípio, chamado de princípio de exclusão de Pauli , afirma que dois elétrons no mesmo átomo não podem ocupar exatamente os mesmos estados quânticos. Ou seja, cada elétron em um átomo possui um conjunto único de números quânticos. Isso limita o número de elétrons que podem ocupar qualquer orbital, subcamada e camada.

Aqui é mostrado o arranjo de elétrons para um átomo de hidrogênio:



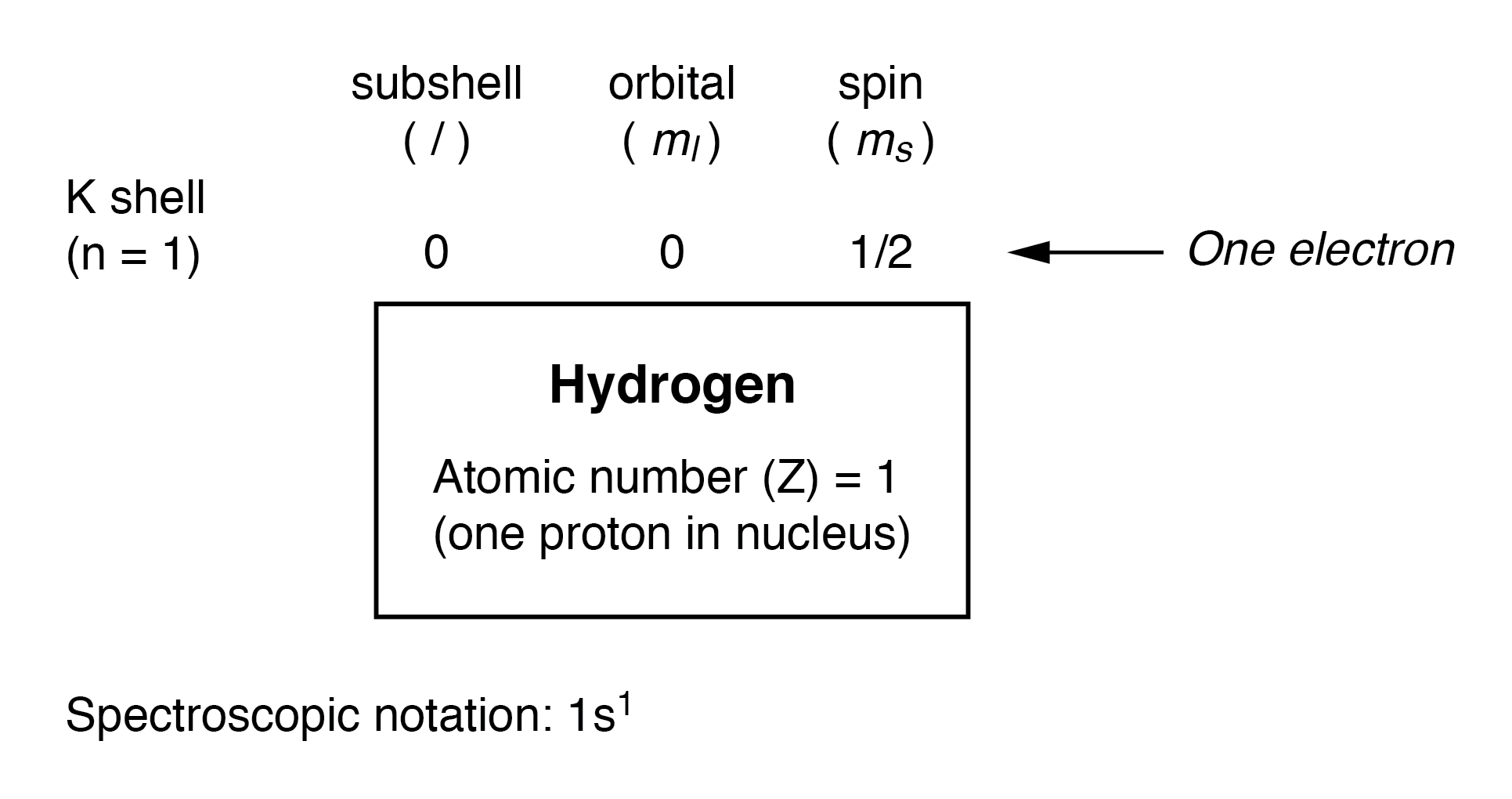
Com um próton no núcleo, é necessário um elétron para equilibrar eletrostaticamente o átomo (a carga elétrica positiva do próton exatamente equilibrada pela carga elétrica negativa do elétron). Este elétron reside na camada mais baixa (n =1), a primeira sub camada (l =0), no único orbital (orientação espacial) dessa sub camada (m _l =0), com um valor de spin de 1/2. Um método comum de descrever esta organização é listar os elétrons de acordo com suas camadas e subcamadas em uma convenção chamada notação espectroscópica . Nesta notação, o número da camada é mostrado como um inteiro, a sub camada como uma letra (s, p, d, f) e o número total de elétrons na sub camada (todos os orbitais, todos os spins) como um sobrescrito. Assim, o hidrogênio, com seu elétron solitário residindo no nível de base, é descrito como 1s ¹ .

Seguindo para o próximo átomo (em ordem do número atômico), temos o elemento hélio:



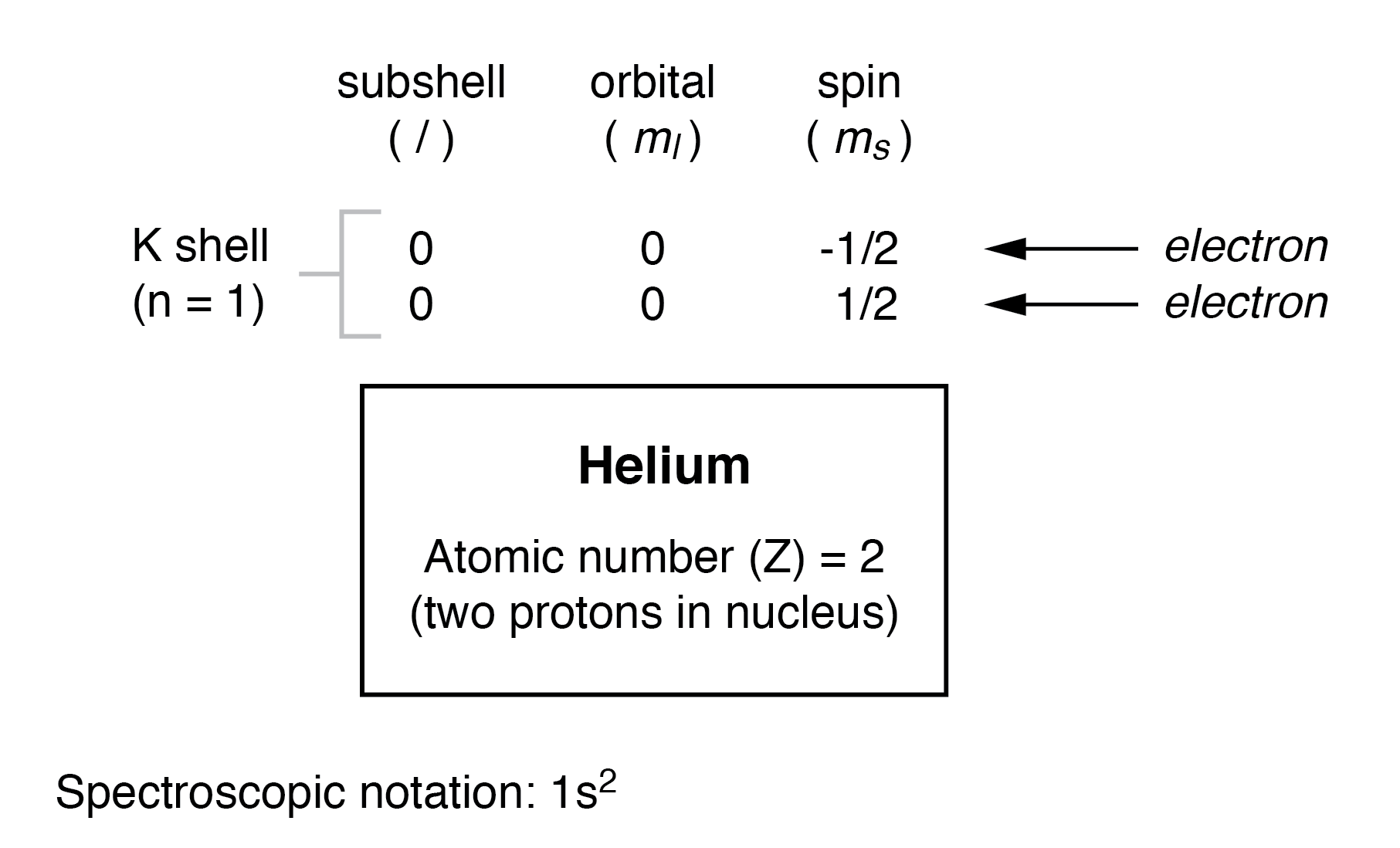
Um átomo de hélio tem dois prótons no núcleo, e para isso são necessários dois elétrons para equilibrar a carga elétrica duplo-positiva. Como dois elétrons - um com spin =1/2 e outro com spin =-1 / 2 - se encaixam em um orbital, a configuração eletrônica do hélio não requer subcamadas ou camadas adicionais para conter o segundo elétron.

No entanto, um átomo que requer três ou mais elétrons irá requerem subcamadas adicionais para conter todos os elétrons, uma vez que apenas dois elétrons caberão na camada inferior (n =1). Considere o próximo átomo na sequência de números atômicos crescentes, o lítio:



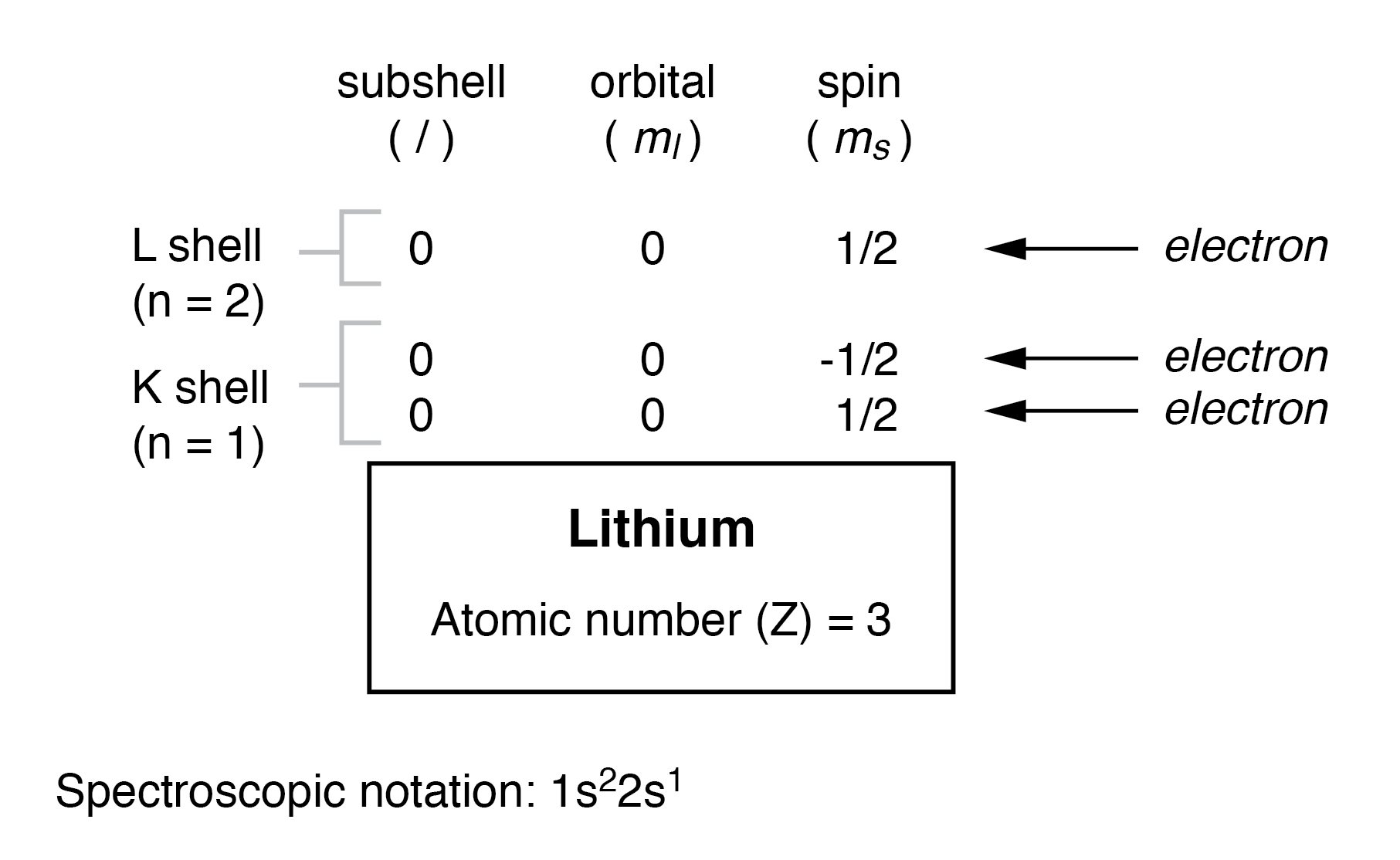
Um átomo de lítio usa uma fração da capacidade da camada L (n =2). Esta camada, na verdade, tem uma capacidade total de oito elétrons (capacidade máxima da camada =2n ² elétrons). Se examinarmos a organização do átomo com uma camada L completamente preenchida, veremos como todas as combinações de subcamadas, orbitais e spins são ocupadas por elétrons:



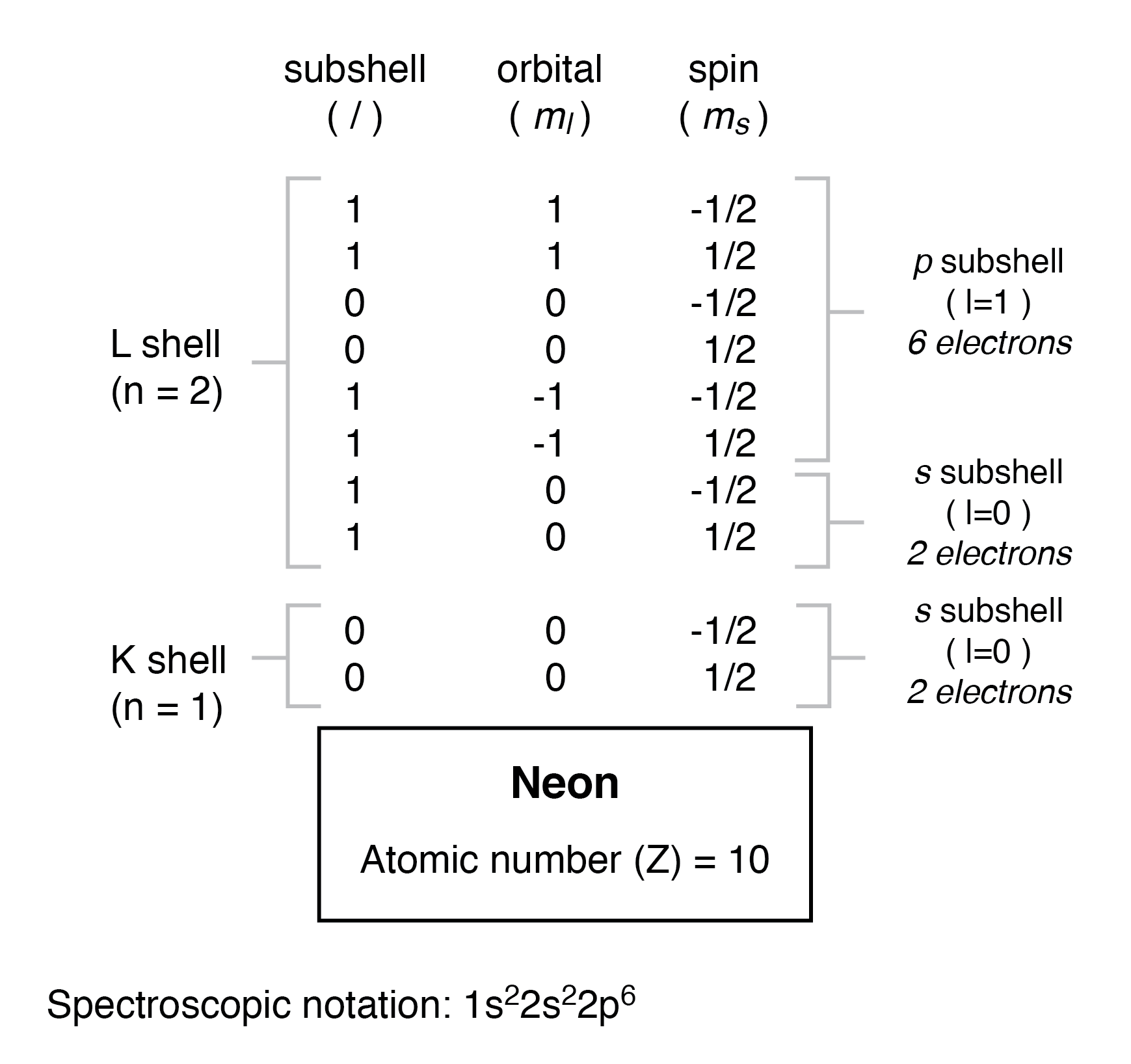
Freqüentemente, quando a notação espectroscópica é fornecida para um átomo, qualquer camada que esteja completamente preenchida é omitida e a camada não preenchida, ou a camada preenchida de nível mais alto, é denotada. Por exemplo, o elemento neon (mostrado na ilustração anterior), que tem duas conchas completamente preenchidas, pode ser espectroscopicamente descrito simplesmente como 2p ⁶ em vez de 1s ² 2s ² 2p ⁶ . O lítio, com sua camada K completamente preenchida e um elétron solitário na camada L, pode ser descrito simplesmente como 2s ¹ em vez de 1s ² 2s ¹ .

A omissão de conchas de nível inferior completamente preenchidas não é apenas uma notação de conveniência. Ele também ilustra um princípio básico da química:que o comportamento químico de um elemento é determinado principalmente por suas conchas vazias. Tanto o hidrogênio quanto o lítio têm um único elétron em suas camadas mais externas (1s ¹ e 2s ¹ , respectivamente), dando aos dois elementos algumas propriedades semelhantes. Ambos são altamente reativos e reativos da mesma maneira (ligando-se a elementos semelhantes em modos semelhantes). Pouco importa que o lítio tenha uma camada K completamente preenchida sob sua camada L quase vazia:a camada L vazia é a que determina seu comportamento químico.

Elementos com camadas externas completamente preenchidas são classificados como nobres , e são distinguidos por não reatividade quase completa com outros elementos. Esses elementos costumavam ser classificados como inertes , quando se pensava que eles eram completamente não reativos, mas agora são conhecidos por formar compostos com outros elementos sob condições específicas.

Tabela Periódica

Como os elementos com configurações eletrônicas idênticas em suas camadas mais externas exibem propriedades químicas semelhantes, Dmitri Mendeleev organizou os diferentes elementos em uma tabela de acordo. Essa tabela é conhecida como tabela periódica dos elementos , e as tabelas modernas seguem esta forma geral na Figura abaixo.



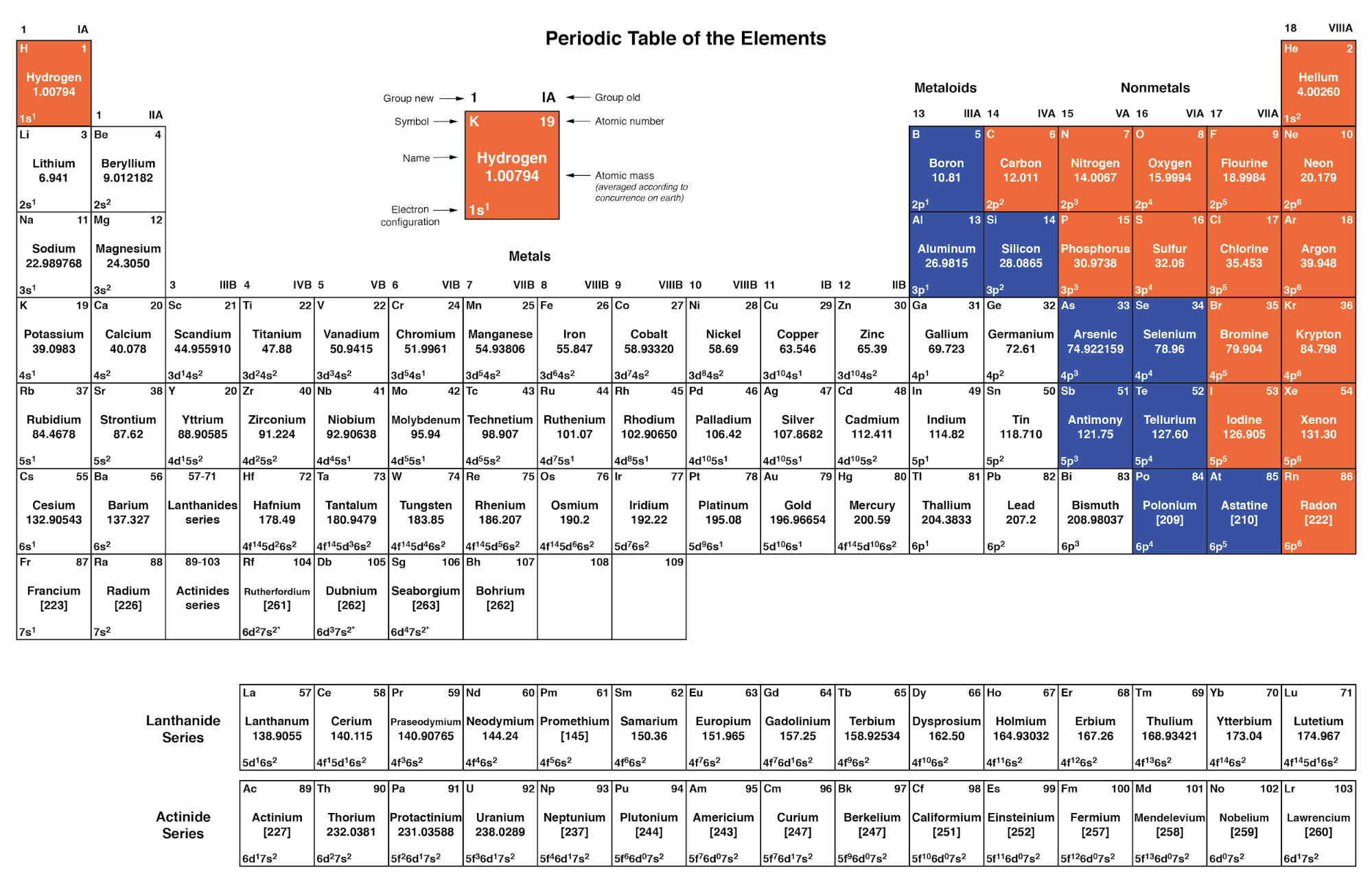
Tabela periódica de elementos químicos

Dmitri Mendeleev, um químico russo, foi o primeiro a desenvolver uma tabela periódica dos elementos. Embora Mendeleev tenha organizado sua tabela de acordo com a massa atômica em vez do número atômico, e tenha produzido uma tabela que não era tão útil quanto as tabelas periódicas modernas, seu desenvolvimento é um excelente exemplo de prova científica. Vendo os padrões de periodicidade (propriedades químicas semelhantes de acordo com a massa atômica), Mendeleev formulou a hipótese de que todos os elementos deveriam se encaixar neste esquema ordenado. Quando ele descobriu pontos “vazios” na mesa, ele seguiu a lógica da ordem existente e hipotetizou a existência de elementos até então não descobertos. A subsequente descoberta desses elementos concedeu legitimidade científica à hipótese de Mendeleev, promovendo futuras descobertas e levando à forma da tabela periódica que usamos hoje.

É assim que a ciência deveria trabalho:hipóteses seguidas até suas conclusões lógicas e aceitas, modificadas ou rejeitadas conforme determinado pela concordância dos dados experimentais com essas conclusões. Qualquer tolo pode formular uma hipótese após o fato para explicar os dados experimentais existentes, e muitos o fazem. O que diferencia uma hipótese científica de post hoc a especulação é a previsão de dados experimentais futuros ainda não coletados, e a possibilidade de refutação como resultado desses dados. Seguir ousadamente uma hipótese até a (s) sua (s) conclusão (ões) lógica (s) e ousar prever os resultados de experimentos futuros não é um ato dogmático de fé, mas sim um teste público dessa hipótese, aberto ao desafio de qualquer pessoa capaz de produzir dados contraditórios. In other words, scientific hypotheses are always “risky” due to the claim to predict the results of experiments not yet conducted, and are therefore susceptible to disproof if the experiments do not turn out as predicted. Thus, if a hypothesis successfully predicts the results of repeated experiments, its falsehood is disproven.

Quantum Mechanics From Hypothesis to Theory

Quantum mechanics, first as a hypothesis and later as a theory, has proven to be extremely successful in predicting experimental results, hence the high degree of scientific confidence placed in it. Many scientists have reason to believe that it is an incomplete theory, though, as its predictions hold true more at micro physical scales than at macro scopic dimensions, but nevertheless it is a tremendously useful theory in explaining and predicting the interactions of particles and atoms.

As you have already seen in this chapter, quantum physics is essential in describing and predicting many different phenomena. In the next section, we will see its significance in the electrical conductivity of solid substances, including semiconductors. Simply put, nothing in chemistry or solid-state physics makes sense within the popular theoretical framework of electrons existing as discrete chunks of matter, whirling around atomic nuclei like miniature satellites. It is when electrons are viewed as “wave functions” existing in definite, discrete states that the regular and periodic behavior of matter can be explained.

REVER:

• Electrons in atoms exist in “clouds” of distributed probability, not as discrete chunks of matter orbiting the nucleus like tiny satellites, as common illustrations of atoms show.
• Individual electrons around an atomic nucleus seek unique “states,” described by four quantum numbers :the Principal Quantum Number , known as the shell; the Angular Momentum Quantum Number , known as the subshell; the Magnetic Quantum Number , describing the orbital (subshell orientation); and the Spin Quantum Number , or simply spin . These states are quantized, meaning that no “in-between” conditions exist for an electron other than those states that fit into the quantum numbering scheme.
• The Principal Quantum Number (n ) describes the basic level or shell that an electron resides in. The larger this number, the greater radius the electron cloud has from the atom’s nucleus, and the greater that electron’s energy. Principal quantum numbers are whole numbers (positive integers).
• The Angular Momentum Quantum Number (l ) describes the shape of the electron cloud within a particular shell or level, and is often known as the “subshell.” There are as many subshells (electron cloud shapes) in any given shell as that shell’s principal quantum number. Angular momentum quantum numbers are positive integers beginning at zero and ending at one less than the principal quantum number (n-1).
• The Magnetic Quantum Number (m _l ) describes which orientation a subshell (electron cloud shape) has. Subshells may assume as many different orientations as 2-times the subshell number (l ) plus 1, (2l+1) (E.g. for l=1, ml=-1, 0, 1) and each unique orientation is called an orbital . These numbers are integers ranging from the negative value of the subshell number (l ) through 0 to the positive value of the subshell number.
• The Spin Quantum Number (m _s ) describes another property of an electron, and may be a value of +1/2 or -1/2.
• Pauli’s Exclusion Principle says that no two electrons in an atom may share the exact same set of quantum numbers. Therefore, no more than two electrons may occupy each orbital (spin=1/2 and spin=-1/2), 2l+1 orbitals in every subshell, and n subshells in every shell, and no more.
• Spectroscopic notation is a convention for denoting the electron configuration of an atom. Shells are shown as whole numbers, followed by subshell letters (s,p,d,f), with superscripted numbers totaling the number of electrons residing in each respective subshell.
• An atom’s chemical behavior is solely determined by the electrons in the unfilled shells. Low-level shells that are completely filled have little or no effect on the chemical bonding characteristics of elements.
• Elements with completely filled electron shells are almost entirely unreactive, and are called noble (formerly known as inert ).

PLANILHAS RELACIONADAS:

• Atomic Structure Worksheet
• Basic Electricity Worksheet