Adição de vetor simples

Lembre-se de que vetores são objetos matemáticos exatamente como números em uma reta numérica:eles podem ser adicionados, subtraídos, multiplicados e divididos. A adição é talvez a operação vetorial mais fácil de visualizar, então vamos começar com isso. Se vetores com ângulos comuns são adicionados, suas magnitudes (comprimentos) somam-se exatamente como as quantidades escalares regulares:(Figura abaixo)







Da mesma forma, se as fontes de tensão CA com o mesmo ângulo de fase forem conectadas em série, suas tensões serão adicionadas exatamente como você poderia esperar com baterias CC:(Figura abaixo)







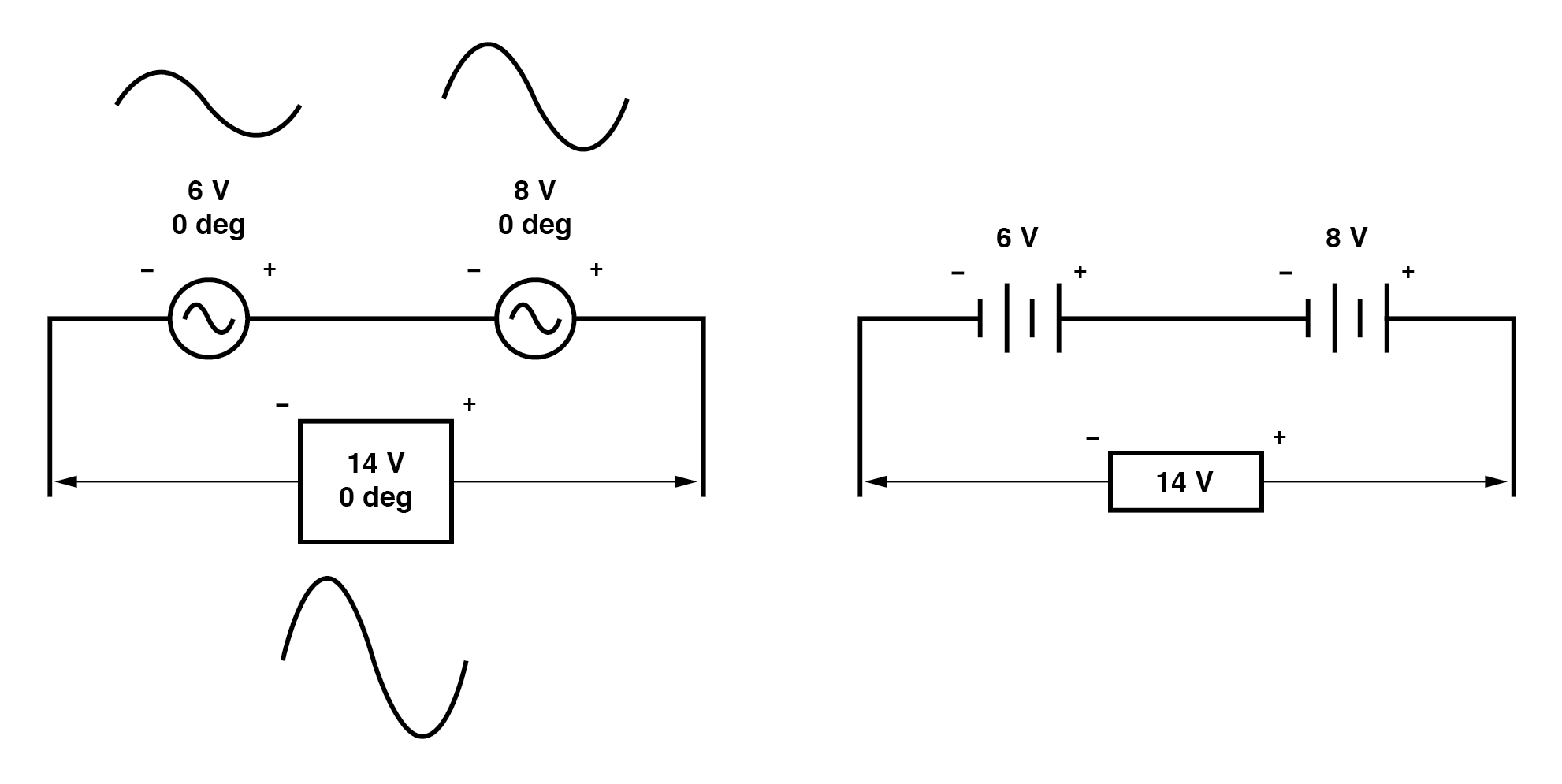
Observe as marcas de polaridade (+) e (-) próximas aos terminais das duas fontes CA. Embora saibamos que a CA não tem "polaridade" no mesmo sentido que a CC, essas marcas são essenciais para saber como fazer referência aos ângulos de fase das tensões. Isso ficará mais evidente no próximo exemplo.

Se os vetores estiverem diretamente opostos (180 ° fora de fase) são somados, suas magnitudes (comprimentos) são subtraídas, assim como as grandezas escalares positivas e negativas subtraem quando adicionadas:(Figura abaixo)







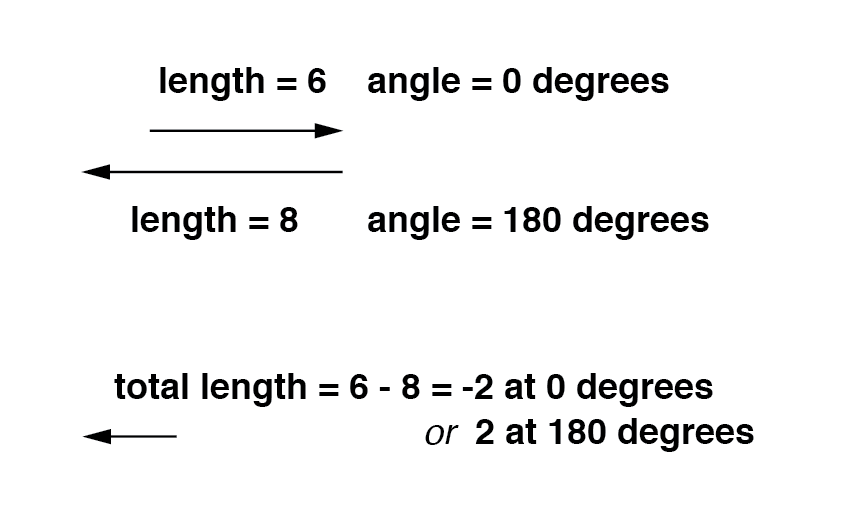
Da mesma forma, se fontes de tensão CA opostas estiverem conectadas em série, suas tensões serão subtraídas como você pode esperar com baterias CC conectadas de forma oposta:(Figura abaixo)







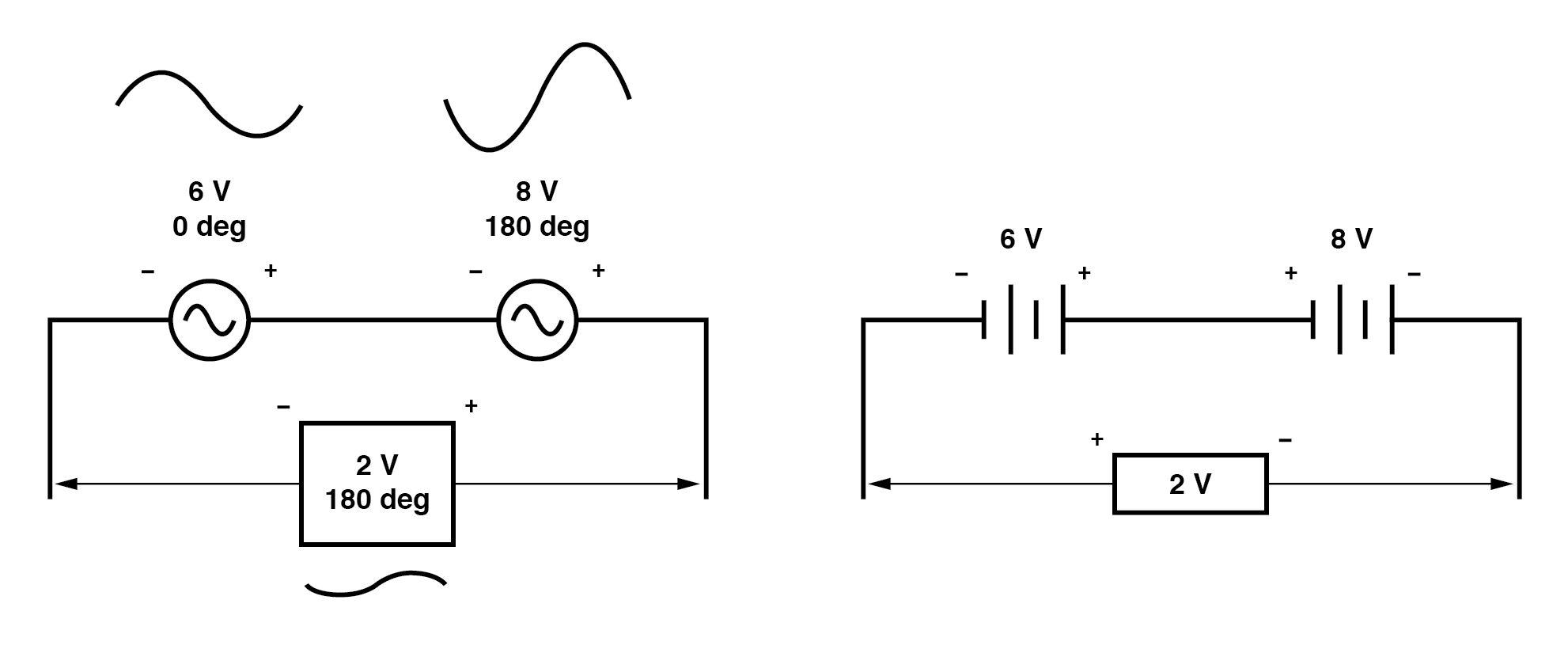
Determinar se essas fontes de tensão estão ou não opostas uma à outra requer um exame de suas marcações de polaridade e seus ângulos de fase. Observe como as marcações de polaridade no diagrama acima parecem indicar tensões aditivas (da esquerda para a direita, vemos - e + na fonte de 6 volts, - e + na fonte de 8 volts).

Mesmo que essas marcações de polaridade normalmente indiquem um aditivo efeito em um circuito CC (as duas tensões trabalhando juntas para produzir uma tensão total maior), neste circuito CA eles estão realmente empurrando em direções opostas porque uma dessas tensões tem um ângulo de fase de 0 ° e o outro um ângulo de fase de 180 ° .

O resultado, é claro, é uma voltagem total de 2 volts.

Poderíamos também ter mostrado as tensões opostas subtraindo em série como esta:(Figura abaixo)







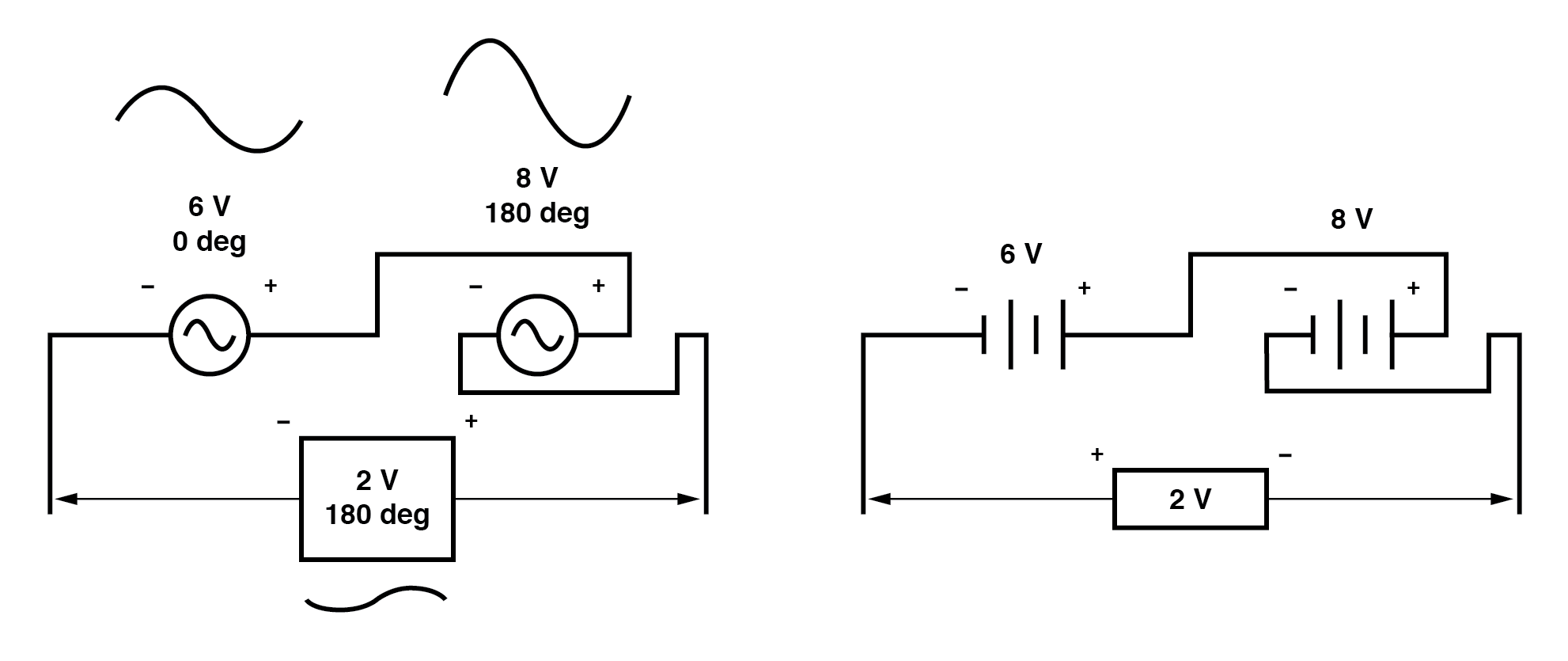
Observe como as polaridades parecem opostas umas às outras agora, devido à reversão das conexões dos fios na fonte de 8 volts.

Uma vez que ambas as fontes são descritas como tendo ângulos de fase iguais (0 ° ), eles realmente se opõem um ao outro e o efeito geral é o mesmo do cenário anterior com polaridades "aditivas" e ângulos de fase diferentes:uma tensão total de apenas 2 volts. (Figura abaixo)

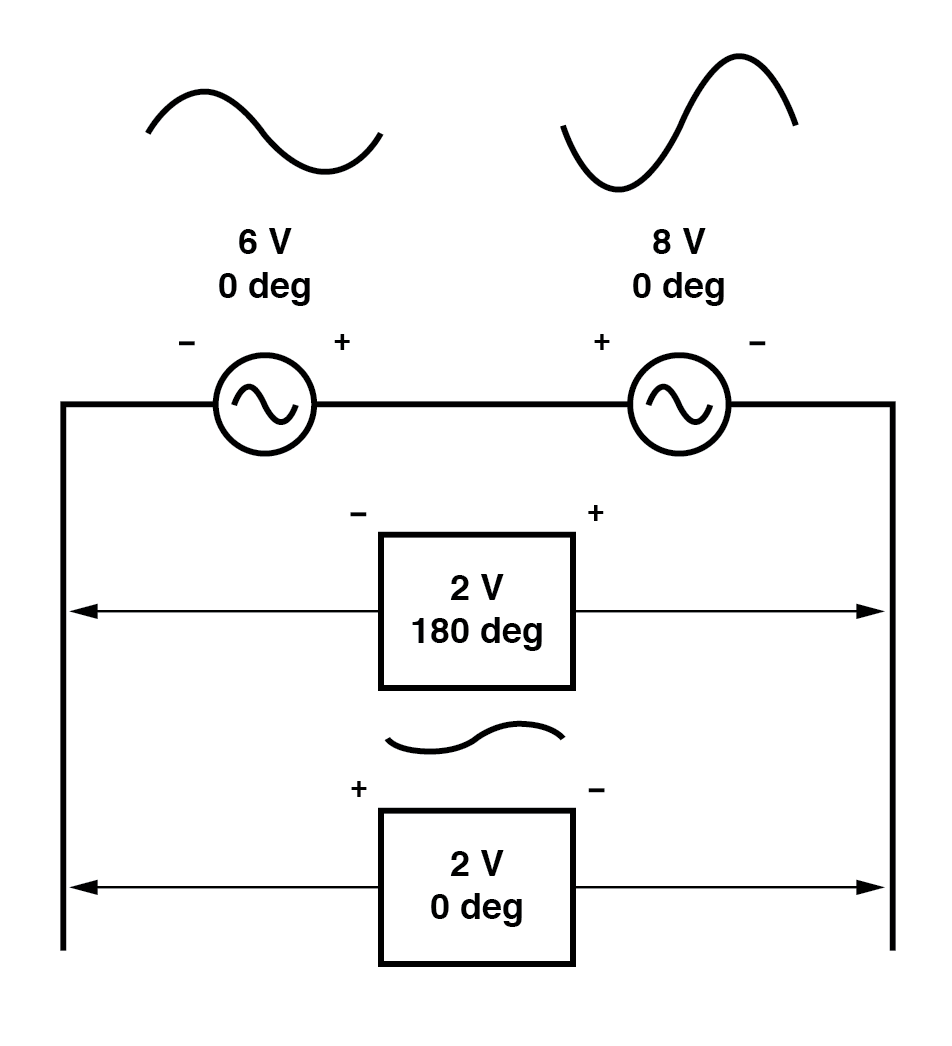
Assim como existem duas maneiras de expressar a fase das fontes, existem duas maneiras de expressar a soma resultante.



A tensão resultante pode ser expressa de duas maneiras diferentes:2 volts a 180 ° com o símbolo (-) à esquerda e o símbolo (+) à direita, ou 2 volts a 0 ° com o símbolo (+) à esquerda e o símbolo (-) à direita. Uma reversão de fios de uma fonte de tensão CA é o mesmo que mudar de fase essa fonte em 180 °. (Figura abaixo)

Exemplo de fontes de tensão equivalentes.



PLANILHAS RELACIONADAS:

• Planilha da fase AC
• Planilha de análise de rede AC