Dependência de temperatura de picos spin-divisão no foco transversal de elétrons
Resumo
Apresentamos resultados experimentais de medições de focalização de elétrons transversais realizadas usando GaAs tipo n. Na presença de um pequeno campo magnético transversal (B ⊥ ), os elétrons são focalizados do injetor para o detector, levando a picos de foco periódicos em B ⊥ . Mostramos que os picos de foco ímpar exibem uma divisão, onde cada subpico representa uma população de um ramo de spin específico que emana do injetor. A dependência da temperatura revela que a divisão do pico é bem definida em baixa temperatura, enquanto que mancha em alta temperatura, indicando que a polarização de rotação orientada por troca no injetor é dominante em baixas temperaturas.
Histórico
O transporte de elétrons através de um sistema quase unidimensional (1D) realizado usando o gás de elétron bidimensional (2DEG) formado na interface da heteroestrutura GaAs / AlGaAs tem sido extensivamente estudado. Um sistema 1D fornece uma plataforma excelente para prever não apenas o sistema mecânico quântico não interagente, onde a quantização de condutância [1-3] está nas unidades de \ (n \ times \ frac {2e ^ {2}} {h} \ ), onde n =1,2,3 ... são diferentes subbaixas de energia 1D, mas também um local para explorar a física de muitos corpos [4-9]. Recentemente, o progresso na física do sistema 1D de muitos corpos ganhou impulso devido à previsão e demonstração experimental de fases ricas no sistema 1D de baixa densidade levando à cristalização incipiente de Wigner [6, 7, 10]. Além disso, a origem da anomalia de condutância de 0,7 na estrutura do sistema 1D de muitos corpos ainda é debatida [11-15]. A anomalia 0,7 tem duas características principais:primeiro, na presença de um campo magnético no plano, a anomalia 0,7 evolui para um platô \ (0,5 \ vezes \ frac {2e ^ {2}} {h} \), que o indica é relacionado ao spin [4]; em segundo lugar, constatou-se que a anomalia de 0,7 enfraquece (fortalece) com a diminuição (aumento) da temperatura [4]. Essas observações notáveis levaram a um grande volume de tentativas teóricas e experimentais de sondar a polarização de spin intrínseca associada à anomalia de 0,7; no entanto, não há consenso como tal sobre a origem desta anomalia [11-15]. Portanto, para esclarecer melhor a anomalia de 0,7, é essencial realizar uma medição direta da polarização do spin em um canal 1D.
Um esquema baseado em focalização transversal de elétrons (TEF) foi proposto para abordar a polarização de spin [16, 17] e foi validado em GaAs tipo p [18, 19] e InSb tipo n [20]. Dentro desse esquema, a polarização de spin decorrente da interação de troca pode ser extraída da assimetria dos dois subpicos do primeiro pico de focalização. Recentemente, mostramos que a injeção de elétrons 1D cujos spins foram separados espacialmente pode ser detectada na forma de uma divisão no primeiro pico de focalização, onde os dois subpicos representam a população de estados de spin detectados [21]. No presente trabalho, relatamos a dependência da temperatura do primeiro pico de foco da divisão do spin e analisamos os resultados com base no gap de spin presente entre as duas espécies de spin.
Método
Os dispositivos estudados no presente trabalho foram fabricados a partir do gás de elétron bidimensional de alta mobilidade (2DEG) formado na interface de GaAs / Al 0,33 Ga 0,67 Como heteroestrutura. Em 1,5 K, a densidade eletrônica medida (mobilidade) era 1,80 × 10 11 cm −2 (2,17 × 10 6 cm 2 V −1 s −1 ), portanto, o caminho livre médio é superior a 10 μ m que é muito maior do que o comprimento de propagação do elétron. Os experimentos foram realizados em um refrigerador de diluição livre de criofrenia com uma temperatura de rede de 20 mK usando a técnica padrão de bloqueio. A faixa de medição da dependência da temperatura foi de 20 mK a 1,8 K.
Resultados e discussão
A Figura 1a mostra a configuração experimental junto com um espectro de focagem típico obtido usando o dispositivo mostrado na inserção. O dispositivo de focalização é especialmente projetado para que o injetor e o detector possam ser controlados separadamente para evitar uma possível interferência entre eles [21-23]. O fio quântico usado para o injetor e detector tem largura (direção de confinamento) de 500 nm e comprimento (direção do fluxo de corrente) de 800 nm. Tanto o injetor quanto o detector mostram platôs de condutância bem definidos, conforme mostrado na Fig. 1 b. Mais detalhes sobre o dispositivo são fornecidos na legenda da Fig. 1.
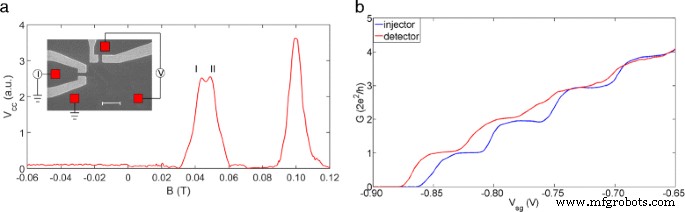
A configuração do experimento e as características do dispositivo. a Um gráfico representativo do foco transversal de elétrons com o injetor e o detector configurados para G 0 (2e 2 / h). V cc é a queda de tensão no detector. Os picos de foco são bem definidos com um campo magnético positivo e o sinal é insignificante com um campo magnético negativo. O primeiro pico mostra uma divisão pronunciada. Os dois subpicos foram destacados como pico I e pico II. A inserção mostra uma imagem SEM do dispositivo. A separação entre o injetor e o detector é de 1,5 μ m. Quadrados vermelhos formam os contatos ôhmicos, enquanto dois pares de portas de cor cinza, esquerda e superior, formam o injetor e o detector, respectivamente. A barra de escala é 2 μ m. b Características de condutância do injetor e detector
Com o campo magnético negativo, o sinal medido é quase zero porque os elétrons se dobram na direção oposta e, portanto, perdem o detector. Também é evidente que a oscilação de Shubnikov-de Haas e o efeito Hall quântico não contribuem para a observação. Na presença de um pequeno campo magnético transversal positivo (B ⊥ ) os elétrons são focados do injetor para o detector, levando a picos de foco periódicos em B ⊥ enquanto o sinal detectado é insignificante na extremidade do campo magnético negativo. A periodicidade calculada de 60 mT usando a relação [23],
$$ B_ {focus} =\ frac {\ sqrt {2} \ hbar k_ {F}} {eL} $$ (1)
está de acordo com o resultado experimental. Aqui, e é a carga elementar e \ (\ hbar \) é a constante de Planck reduzida, L é a separação entre o injetor e o detector (na geometria do dispositivo de focalização de 90 °, essa é a separação ao longo da direção diagonal). Além do pico de focalização periódica, que é uma manifestação da órbita cíclotron de elétrons semiclássica, é interessante notar a divisão de picos de focalização ímpares. É sugerido que esta divisão anômala de picos de focalização ímpares surge da interação spin-órbita (SOI) [16, 17] e foi observada com sucesso no gás de buraco GaAs [18, 19] e gás de elétron InSb [20]. Recentemente, demonstramos a divisão de picos de focalização ímpares em n-GaAs [21], onde um fio quântico mais longo possuindo elétrons 1D parcialmente polarizados e espacialmente separados foi usado para injetar os elétrons 1D polarizados no regime 2D e, subsequentemente, medido através do detector no forma de uma divisão no primeiro pico de foco. Aqui, estamos interessados em investigar o efeito térmico nos estados de spin dentro do canal 1D por meio do foco transversal de elétrons. Notamos que a divisão desaparece quando a energia térmica k B T excede 2 Δ E ( Δ E é a diferença de energia entre os dois ramos de spin) concordando com a previsão teórica [17].
Antes de discutirmos o efeito da dependência da temperatura, é importante entender o mecanismo responsável pela divisão do pico observada. A Figura 2 a, b mostra o perfil de potencial das portas divididas formando o injetor (par inferior) e o detector (par esquerdo). Na presença de SOI, as duas espécies de spin seguem raios de ciclotron diferentes, como mostrado na Fig. 2a, resultando assim em dois subpicos no primeiro pico de focalização. No entanto, a situação é diferente para o segundo pico de foco, onde um espalhamento no limite do potencial eletrostático criado pelas portas divididas está envolvido, como mostrado na Fig. 2b. Neste caso, um elétron de spin-up (seta vermelha nos gráficos de cores) segue inicialmente um raio de ciclotron menor, embora possua um raio maior após o espalhamento [16, 17] e vice-versa para o elétron de spin-down (seta branca) , assim, as duas espécies de spin se juntam novamente no detector. O raciocínio subjacente para a divisão do pico pode ser encontrado no espaço k na Fig. 2 c, d. Aqui, assumimos que a interação spin-órbita é do tipo Rashba; no entanto, a análise é válida para o efeito Dresselhaus em massa também. Para o primeiro pico de focagem (Fig. 2 c), as duas espécies de spin viajam de (0, k y ) para (-k x , 0) ao longo de diferentes superfícies de Fermi. Para o segundo pico de focalização (Fig. 2 d), o mesmo argumento é verdadeiro antes do espalhamento; entretanto, o momento muda de sinal enquanto a orientação do spin permanece preservada após o espalhamento [16]. Portanto, um elétron de spin-up (setas vermelhas) ocupando inicialmente a superfície interna de Fermi salta para a superfície externa de Fermi após o espalhamento para garantir que tanto o sinal do momento quanto a orientação do spin estejam na ordem correta (o salto é destacado por a seta azul grossa na Fig. 2 d) e vice-versa para o elétron spin-down. O raio do cíclotron é proporcional ao momento, de modo que a alternância no raio do cíclotron ocorre no espaço de coordenadas como consequência do salto entre duas superfícies de Fermi que leva a um único pico de focalização segundo.
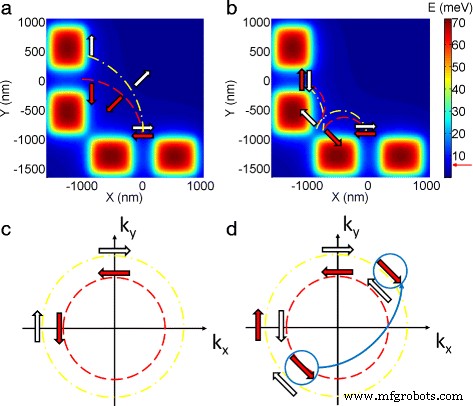
Mecanismo de divisão de pico. a , b Divisão de pico no espaço de coordenadas para o primeiro e o segundo picos de focagem, respectivamente. As setas vermelhas e brancas representam elétrons de spin-up e spin-down, os blocos coloridos representam o potencial eletrostático e o traço tracejado em vermelho tem raio de ciclotron menor, enquanto o traço de ponto amarelo tem raio de ciclotron maior. c , d Divisão de pico no espaço k para o primeiro e segundo picos de focagem, respectivamente. Os elétrons viajam de (0, k y ) para (-k x , 0) sentido anti-horário no gráfico ( c ) No enredo ( d ), a seta azul grossa destaca a transição após reflexão no limite do potencial eletrostático formado entre o injetor e o detector
A Figura 3 a – c mostra a dependência da temperatura dos resultados de focagem com o injetor definido para 0,5 G 0 , G 0 e 1.8G 0 , respectivamente, onde a temperatura da rede é incrementada de 20 mK (a temperatura do elétron é calibrada para ser em torno de 70 mK) a 1,8 K, e a Fig. 3 d – f mostra o zoom-in dos dados na Fig. 3 a – c , respectivamente. Para G i =0,5G 0 (Fig. 3 a) um único pico é observado (já que apenas uma sub-banda de spin está ocupada), que se alarga gradualmente em temperaturas mais altas. Além disso, o pico de foco muda em direção ao centro do espectro e se torna mais simétrico em temperaturas mais altas (veja o traço inferior, T =1,8 K, Fig. 3 a, d). Isso pode ser devido a uma possível transição de elétrons entre as duas sub-bandas de spin a uma temperatura relativamente alta. Em comparação, para G i = G 0 (Fig. 3 b), os subpicos, cada um representando um estado de spin, estão presentes de 20 mK até 1,2 K. No entanto, a queda no primeiro pico de focagem levando a dois subpicos mancha em 1,8 K ( Fig. 3 b, e). Com G i definido como 1.8 G 0 (Fig. 3 c), a divisão não é bem resolvida e o subpico esquerdo (I) domina o espectro. Notamos que ao aumentar a temperatura, o pico I reduziu gradualmente em amplitude para resultar em um primeiro pico de focagem assimétrico a 1,8 K. No InSb tipo n, a divisão foi pronunciada mesmo a 10 K, o que é consistente com o fato do pico o desdobramento foi em torno de 60 mT, uma indicação de forte SOI no InSb [20], que é uma ordem maior do que o desdobramento do pico de 5,5 mT medido no presente caso.
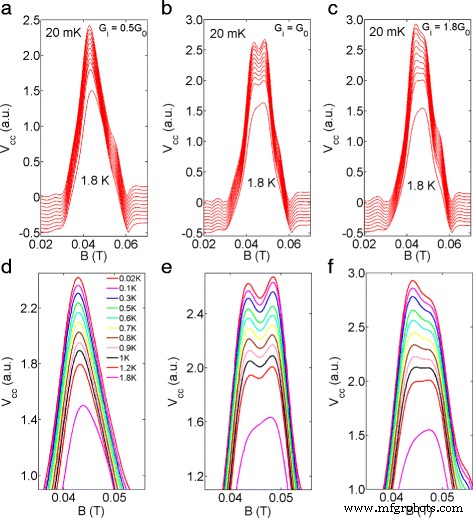
Dependência de temperatura de TEF. a - c O injetor foi definido para 0,5 G 0 , G 0 e 1.8G 0 , respectivamente. A temperatura da rede foi incrementada de 20 mK (traço superior) para 1,8 K (traço inferior). Os dados foram deslocados verticalmente para maior clareza. d - f , amplie os dados em ( a ) - ( c )
Para extrair a largura e a amplitude do pico com precisão, considerando que os dois subpicos podem se sobrepor parcialmente, usamos dois picos Lorentzianos para reconstruir os dados experimentais como mostrado na Fig. 4a usando a relação,
$$ A (B) =\ sum \ limits_ {i =1,2} A_ {i} \ times \ frac {\ gamma_ {i} ^ {2}} {\ gamma_ {i} ^ {2} + (B -B_ {i}) ^ {2}} $$ (2)
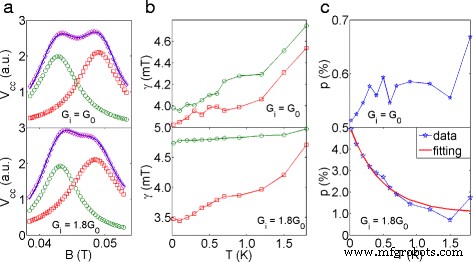
Análise dos dados de dependência da temperatura. Os gráficos no topo são para G i = G 0 , os inferiores são para G i =1.8 G 0 . a Reconstruindo o primeiro pico de focagem com dois picos Lorentzianos a 20 mK. A linha azul sólida são os dados experimentais, o marcador redondo verde é o ajuste para o pico I, o marcador do quadrado vermelho é o ajuste para o pico II e o marcador de diamante magenta destaca o pico de focagem reconstruído. b FHWM, γ em função da temperatura:os sub-picos aumentam com o aumento da temperatura em ambos os casos. Os marcadores representam o mesmo significado que no gráfico ( a ) c A polarização medida com G i = G 0 flutua em torno de 0,6 % . Por outro lado, a polarização medida com G i =1.8 G 0 segue uma queda exponencial
onde A i é a amplitude do pico i ( eu =1, 2 para pico I e pico II, respectivamente), γ i denota a largura total na metade do máximo (FWHM), e B i é o centro do pico. Dois resultados perceptíveis podem ser extraídos do ajuste:primeiro, é visto na Fig. 4b que γ (ver legenda da Fig. 4 para detalhes sobre traços e símbolos que representam o pico I e o pico II) para ambos os picos I e II aumentam com o aumento da temperatura, independentemente da condutância do injetor, que indica que o alargamento térmico dos subpicos impede a observação de divisão de pico em alta temperatura. Pode-se notar que pico I para G i =1.8 G 0 é relativamente robusto contra a temperatura em comparação com outros picos (ambos os picos de G 0 e pico II de 1,8 G 0 ) Em segundo lugar, a polarização de spin medida p \ (\ left (p =\ left | \ frac {A_ {1} -A_ {2}} {A1 + A_ {2}} \ right | \ right) \) com G i = G 0 flutua em torno de 0,6 % e não mostra nenhuma dependência explícita com a temperatura, o que concorda com o fato de que a polarização do spin no platô de condutância deve permanecer em 0, independentemente da temperatura (Fig. 4 c, gráfico superior). Por outro lado, quando G i está definido para 1,8 G 0 , a polarização de spin extraída decai de 5 para 0,8 % (Fig. 4 d, gráfico inferior) seguindo a relação [15],
$$ p =\ alpha exp \ left (- \ frac {k_ {B} T} {\ Delta E} \ right) + c $$ (3)
onde α é um prefator responsável pela amplitude, k B é a constante de Boltzmann, Δ E é a diferença de energia entre os dois ramos de spin e c explica o pequeno valor residual que surge da incerteza no experimento. Extraímos o valor de Δ E estar em torno de 0,041 meV (correspondendo a 0,5 K). A teoria [17] prevê que a divisão deve persistir até k B T excede 2 Δ E (ou seja, 1 K no nosso caso), o que concorda razoavelmente bem com o nosso resultado de que a divisão do pico é observável até 1,2 K.
Conclusão
Em conclusão, mostramos a dependência do elétron transversal com a temperatura, onde a contribuição dos dois estados de spin se manifestou como dois sub-picos no primeiro pico de foco. Observou-se que a divisão do pico é bem definida de 20 mK até 1,2 K e além dessa temperatura a divisão do pico espalhou-se. Além disso, o pico de foco tende a se tornar mais simétrico em temperaturas mais altas, indicando um possível equilíbrio entre os dois ramos de spin devido à excitação térmica.
O trabalho é financiado pelo Conselho de Pesquisa em Ciências Físicas e Engenharia (EPSRC), do Reino Unido.
Nanomateriais



