Teoremas de DeMorgan

Um matemático chamado DeMorgan desenvolveu um par de regras importantes com relação à complementação de grupo na álgebra booleana.

Por grupo complementação, refiro-me ao complemento de um grupo de termos, representado por uma barra longa sobre mais de uma variável.

Você deve se lembrar do capítulo sobre portas lógicas que inverter todas as entradas em uma porta inverte a função essencial dessa porta de E para OU, ou vice-versa, e também inverte a saída.

Assim, uma porta OR com todas as entradas invertidas (uma porta Negativa-OR) se comporta da mesma forma que uma porta NAND, e uma porta AND com todas as entradas invertidas (uma porta Negativa-AND) se comporta da mesma forma que uma porta NOR.

Os teoremas de DeMorgan afirmam a mesma equivalência na forma "reversa":que inverter a saída de qualquer porta resulta na mesma função que o tipo oposto de porta (E vs. OU) com entradas invertidas:







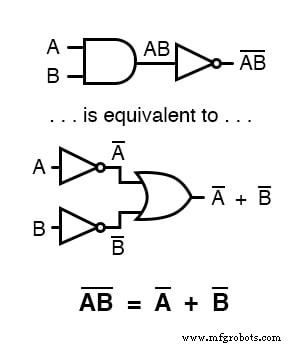
Uma barra longa que se estende ao longo do termo AB atua como um símbolo de agrupamento e, como tal, é totalmente diferente do produto de A e B invertidos independentemente.

Em outras palavras, (AB) 'não é igual a A'B'. Como o símbolo "primo" (') não pode ser estendido sobre duas variáveis ​​como uma barra pode, somos forçados a usar parênteses para aplicá-lo a todo o termo AB na frase anterior.

Uma barra, no entanto, atua como seu próprio símbolo de agrupamento quando esticada sobre mais de uma variável.

Isso tem um impacto profundo em como as expressões booleanas são avaliadas e reduzidas, como veremos.

Teorema de DeMorgan

O teorema de DeMorgan pode ser pensado em termos de quebra um símbolo de barra longa.

Quando uma barra longa é quebrada, a operação diretamente abaixo da quebra muda de adição para multiplicação, ou vice-versa, e os pedaços de barra quebrada permanecem sobre as variáveis ​​individuais. Ilustrar:







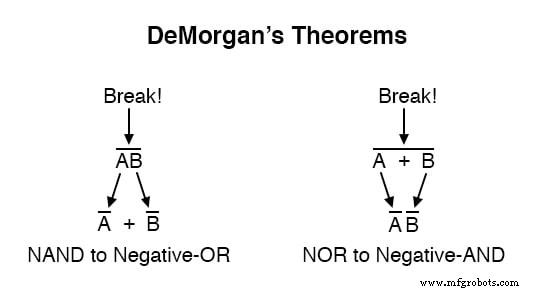
Quando existem várias “camadas” de barras em uma expressão, você só pode quebrar uma barra por vez , e geralmente é mais fácil começar a simplificação quebrando a barra mais longa (mais acima) primeiro.

Para ilustrar, vamos pegar a expressão (A + (BC) ’)’ e reduzi-la usando os teoremas de DeMorgan:









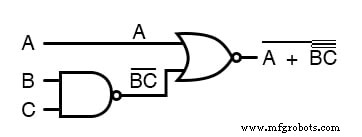
Seguindo o conselho de quebrar a barra mais longa (superior) primeiro, começarei quebrando a barra que cobre toda a expressão como uma primeira etapa:







Como resultado, o circuito original é reduzido a uma porta AND de três entradas com a entrada A invertida:







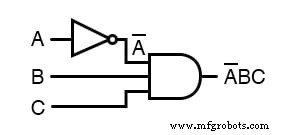
Você deve nunca quebrar mais de uma barra em uma única etapa, conforme ilustrado aqui:







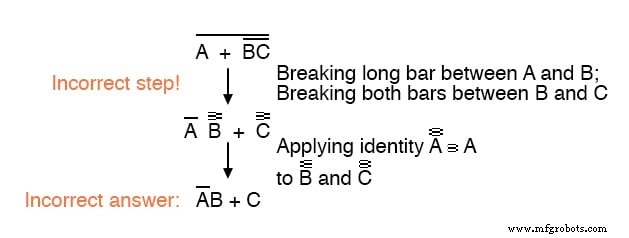
Por mais tentador que seja economizar etapas e quebrar mais de uma barra de cada vez, isso geralmente leva a um resultado incorreto, então não faça isso!

É possível reduzir adequadamente essa expressão quebrando a barra curta primeiro, em vez da barra longa primeiro:







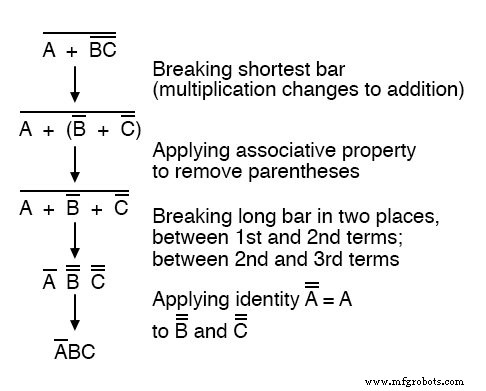
O resultado final é o mesmo, mas são necessárias mais etapas em comparação com o uso do primeiro método, em que a barra mais longa foi quebrada primeiro.

Observe como na terceira etapa quebramos a barra longa em dois lugares.

Esta é uma operação matemática legítima, e não o mesmo que quebrar duas barras em uma etapa!

A proibição de quebrar mais de uma barra em uma etapa não proibição de quebrar uma barra em mais de um lugar.

Quebra em mais de um lugar em uma única etapa está tudo bem; quebrando mais de uma barra em uma única etapa não é.

Você pode estar se perguntando por que os parênteses foram colocados em torno da subexpressão B ’+ C’, considerando o fato de que acabei de removê-los na próxima etapa.

Fiz isso para enfatizar um aspecto importante, mas facilmente negligenciado do teorema de DeMorgan.

Uma vez que uma barra longa funciona como um símbolo de agrupamento, as variáveis ​​anteriormente agrupadas por uma barra quebrada devem permanecer agrupadas para que a precedência apropriada (ordem de operação) não seja perdida.

Neste exemplo, realmente não importaria se eu esquecesse de colocar parênteses depois de quebrar a barra curta, mas em outros casos poderia.

Considere este exemplo, começando com uma expressão diferente:









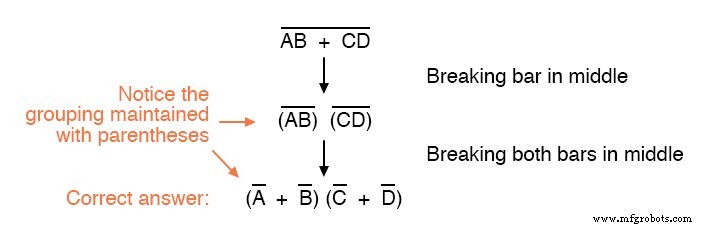
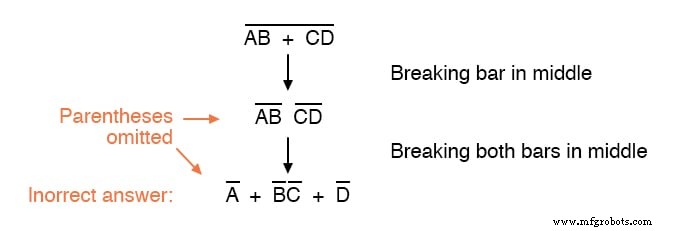
Como você pode ver, manter o agrupamento implícito nas barras de complementação desta expressão é fundamental para obter a resposta correta.

Vamos aplicar os princípios dos teoremas de DeMorgan para a simplificação de um circuito de portão:







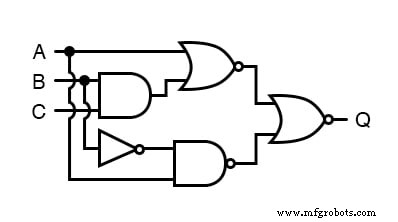
Como sempre, nosso primeiro passo para simplificar esse circuito deve ser gerar uma expressão booleana equivalente.

Podemos fazer isso colocando um rótulo de subexpressão na saída de cada porta, conforme as entradas se tornam conhecidas. Esta é a primeira etapa deste processo:







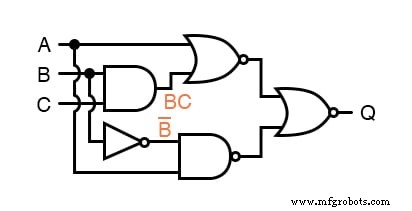
A seguir, podemos rotular as saídas da primeira porta NOR e da porta NAND.

Ao lidar com portas de saída invertida, acho mais fácil escrever uma expressão para a saída da porta sem a inversão final, com uma seta apontando para um pouco antes da bolha de inversão.

Então, no fio que sai do portão (após a bolha), escrevo a expressão completa e complementada.

Isso ajuda a garantir que eu não me esqueça de uma barra complementar na subexpressão, obrigando-me a dividir a tarefa de escrita da expressão em duas etapas:







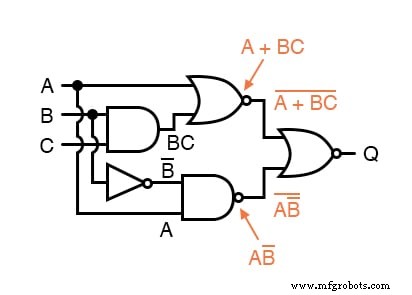
Finalmente, escrevemos uma expressão (ou par de expressões) para a última porta NOR:







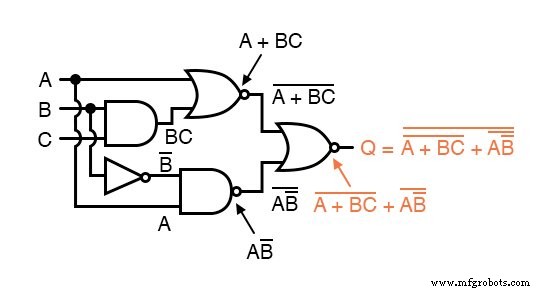
Agora, reduzimos esta expressão usando as identidades, propriedades, regras e teoremas (DeMorgan's) da álgebra booleana:







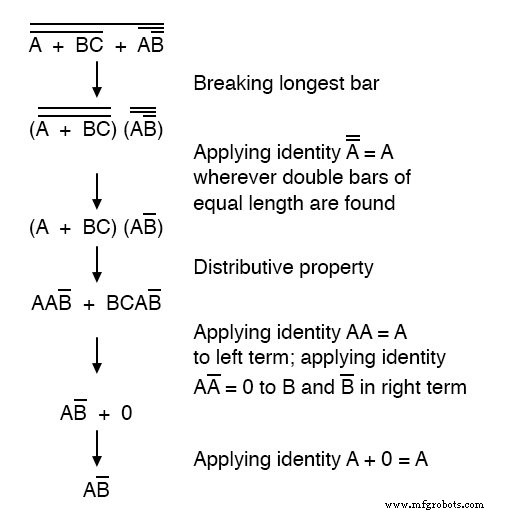
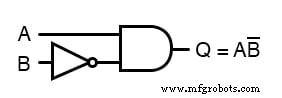
O circuito de porta equivalente para esta expressão muito simplificada é o seguinte:







REVER:

• Os teoremas de DeMorgan descrevem a equivalência entre portas com entradas invertidas e portas com saídas invertidas. Simplificando, uma porta NAND é equivalente a uma porta Negativa-OR e uma porta NOR é equivalente a uma porta Negativa-AND.
• Ao “quebrar” uma barra de complementação em uma expressão booleana, a operação diretamente abaixo da quebra (adição ou multiplicação) é revertida e os pedaços da barra quebrada permanecem sobre os respectivos termos.
• Geralmente é mais fácil abordar um problema quebrando a barra mais longa (mais acima) antes de quebrar qualquer barra abaixo dela. Você deve nunca tente quebrar duas barras em uma etapa!
• As barras de complementação funcionam como símbolos de agrupamento. Portanto, quando uma barra é quebrada, os termos abaixo dela devem permanecer agrupados. Os parênteses podem ser colocados ao redor desses termos agrupados como uma ajuda para evitar a mudança de precedência.

PLANILHAS RELACIONADAS:

• Planilha de álgebra booleana