Harmônicos em sistemas de potência polifásicos

No capítulo sobre sinais de frequência mista, exploramos o conceito de harmônicos em sistemas CA:frequências que são múltiplos inteiros da frequência da fonte fundamental.

Com sistemas de energia CA em que a forma de onda da tensão da fonte proveniente de um gerador CA (alternador) deve ser uma onda senoidal de frequência única, não distorcida, não deve haver conteúdo harmônico. . . idealmente.

Componentes não lineares em sistemas CA

Isso seria verdade se não fosse pelos componentes não lineares . Os componentes não lineares consomem corrente desproporcionalmente em relação à tensão da fonte, causando formas de onda de corrente não senoidais.

Exemplos de componentes não lineares incluem lâmpadas de descarga de gás, dispositivos semicondutores de controle de potência (diodos, transistores, SCRs, TRIACs), transformadores (a corrente de magnetização do enrolamento primário é geralmente não senoidal devido à curva de saturação B / H do núcleo) e motores elétricos (novamente, quando os campos magnéticos dentro do núcleo do motor operam próximos aos níveis de saturação).

Mesmo as lâmpadas incandescentes geram correntes ligeiramente não sinusoidais, pois a resistência do filamento muda ao longo do ciclo devido às rápidas flutuações de temperatura.

Como aprendemos no capítulo de frequência mista, qualquer a distorção de uma forma de onda em forma de onda senoidal constitui a presença de frequências harmônicas.

Quando a forma de onda não sinusoidal em questão é simétrica acima e abaixo de sua linha central média, as frequências harmônicas serão múltiplos inteiros ímpares apenas da frequência da fonte fundamental, sem múltiplos inteiros pares.

A maioria das cargas não lineares produzem formas de onda de corrente como esta e, portanto, harmônicos de números pares (2ª, 4ª, 6ª, 8ª, 10ª, 12ª, etc.) estão ausentes ou apenas minimamente presentes na maioria dos sistemas de energia CA.

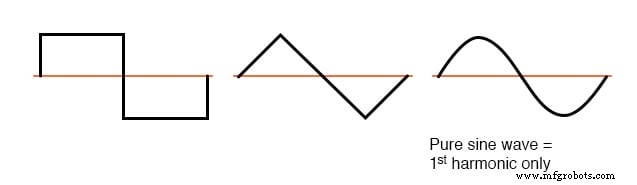
Exemplos de formas de onda simétricas - apenas harmônicos ímpares.



Exemplos de formas de onda não simétricas com harmônicos pares presentes são mostrados para referência na figura abaixo.

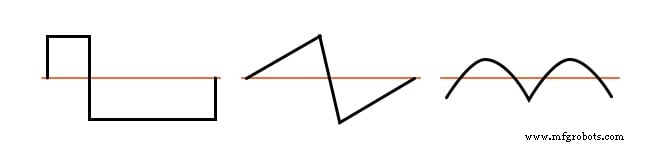
Exemplos de formas de onda não simétricas - até mesmo harmônicos presentes.



Mesmo que metade das frequências harmônicas possíveis sejam eliminadas pela distorção tipicamente simétrica de cargas não lineares, os harmônicos ímpares ainda podem causar problemas. Alguns desses problemas são gerais para todos os sistemas de energia, monofásicos ou outros.

O superaquecimento do transformador devido a perdas por correntes parasitas, por exemplo, pode ocorrer em qualquer Sistema de energia CA onde há um conteúdo harmônico significativo.

No entanto, existem alguns problemas causados ​​por correntes harmônicas que são específicas de sistemas de potência polifásicos, e são esses problemas aos quais esta seção é especificamente dedicada.

Simulação SPICE em relação aos efeitos harmônicos

É útil ser capaz de simular cargas não lineares no SPICE para evitar muita matemática complexa e obter uma compreensão mais intuitiva dos efeitos harmônicos.

Simulação Linear do Sistema AC

Primeiro, vamos começar nossa simulação com um circuito CA muito simples:uma única fonte de tensão de onda senoidal com uma carga puramente linear e todas as resistências associadas:

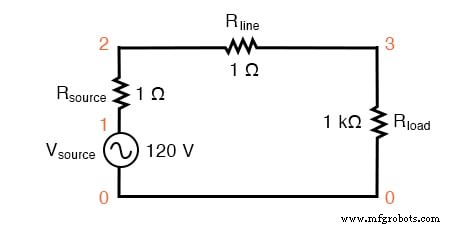
Circuito SPICE com uma única fonte de onda senoidal.



O R _fonte e R _linha resistências neste circuito fazem mais do que apenas imitar o mundo real:eles também fornecem resistências shunt convenientes para medir correntes na simulação SPICE:ao ler a tensão em uma resistência de 1 Ω, você obtém uma indicação direta de corrente através dela, uma vez que E =IR .

Uma simulação SPICE deste circuito (listagem SPICE:"simulação de carga linear") com análise de Fourier na tensão medida em R _linha deve nos mostrar o conteúdo harmônico da corrente de linha deste circuito. Sendo completamente linear por natureza, não devemos esperar nenhuma outra harmônica além da 1ª (fundamental) de 60 Hz, assumindo uma fonte de 60 Hz.

Consulte a saída SPICE “Componentes de Fourier da resposta transitória v (2,3)” e a figura abaixo.

 simulação de carga linear vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k .options itl5 =0 .tran 0,5m 30m 0 1u .plot tran v (2,3) .quatro 60 v (2,3) .fim 

 Componentes de Fourier da resposta transitória v (2,3) componente dc =4.028E-12 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0,000 2 1.200E + 02 5.793E-12 0.000000 51.122 123.122 3 1.800E + 02 7.407E-12 0.000000 -34.624 37.376 4 2,400E + 02 9,056E-12 0,000000 4,267 76,267 5 3.000E + 02 1.651E-11 0.000000 -83.461 -11.461 6 3,600E + 02 3,931E-11 0,000000 36,399 108,399 7 4,200E + 02 2,338E-11 0,000000 -41,343 30,657 8 4,800E + 02 4,716E-11 0,000000 53,324 125,324 9 5,400E + 02 3,453E-11 0,000000 21,691 93,691 distorção harmônica total =0,000000 por cento 

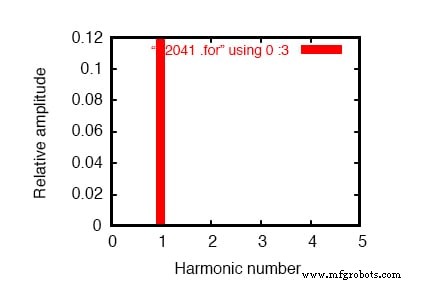
Gráfico de domínio de frequência do componente de frequência único. Veja a lista de SPICE:“simulação de carga linear”.



Um comando .plot aparece na netlist do SPICE e normalmente isso resultaria em uma saída de gráfico de onda senoidal. Neste caso, no entanto, omiti propositalmente a exibição da forma de onda por uma questão de brevidade - o comando .plot está na netlist simplesmente para satisfazer uma peculiaridade da função de transformada de Fourier do SPICE.

Nenhuma transformada discreta de Fourier é perfeita e, portanto, vemos correntes harmônicas muito pequenas indicadas (na faixa de pico-amp!) Para todas as frequências até a 9ª harmônica (na tabela), que é o máximo que o SPICE vai na execução da análise de Fourier .

Mostramos 0,1198 amperes (1,198E-01) para o “componente de Fourier” do 1º harmônico, ou a frequência fundamental, que é nossa corrente de carga esperada:cerca de 120 mA, dada uma tensão de fonte de 120 volts e uma resistência de carga de 1 kΩ.

Simulação de sistema CA monofásico não linear simples

Em seguida, gostaria de simular uma carga não linear para gerar correntes harmônicas. Isso pode ser feito de duas maneiras fundamentalmente diferentes. Uma maneira é projetar uma carga usando componentes não lineares, como diodos ou outros dispositivos semicondutores que são fáceis de simular com SPICE. Outra é adicionar algumas fontes de corrente AC em paralelo com o resistor de carga.

O último método é frequentemente preferido pelos engenheiros para simular harmônicos, uma vez que fontes de corrente de valor conhecido se prestam melhor à análise matemática de rede do que componentes com características de resposta altamente complexas.

Já que estamos deixando o SPICE fazer todo o trabalho matemático, a complexidade de um componente semicondutor não nos causaria problemas, mas como as fontes de corrente podem ser ajustadas para produzir qualquer quantidade arbitrária de corrente (um recurso conveniente), irei escolha a última abordagem mostrada na figura abaixo e na lista SPICE “Simulação de carga não linear”.

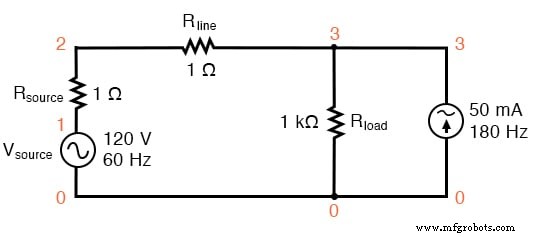
Circuito SPICE:fonte de 60 Hz com 3ª harmônica adicionada.

 Simulação de carga não linear vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) .options itl5 =0 .tran 0,5m 30m 0 1u .plot tran v (2,3) .quatro 60 v (2,3) .fim 

Neste circuito, temos uma fonte de corrente de magnitude 50 mA e uma frequência de 180 Hz, que é três vezes a frequência da fonte de 60 Hz. Conectado em paralelo com o resistor de carga de 1 kΩ, sua corrente será adicionada à do resistor para formar uma corrente de linha total não senoidal.

Vou mostrar o gráfico da forma de onda na figura abaixo apenas para que você possa ver os efeitos dessa corrente de 3ª harmônica na corrente total, que normalmente seria uma onda senoidal simples.

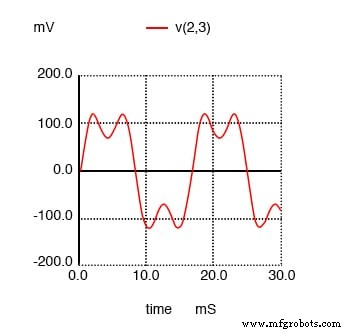
Gráfico de domínio de tempo SPICE mostrando a soma da fonte de 60 Hz e da 3ª harmônica de 180 Hz.

 Componentes de Fourier da resposta transitória v (2,3) componente dc =1.349E-11 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0,000 2 1.200E + 02 1.609E-11 0.000000 67.570 139.570 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2,400E + 02 1,074E-10 0,000000 -169,546 -97,546 5 3,000E + 02 3,871E-11 0,000000 169,582 241,582 6 3,600E + 02 5,736E-11 0,000000 140,845 212,845 7 4,200E + 02 8,407E-11 0,000000 177,071 249,071 8 4,800E + 02 1,329E-10 0,000000 156,772 228,772 9 5,400E + 02 2,619E-10 0,000000 160,498 232,498 distorção harmônica total =41,6666663 por cento 

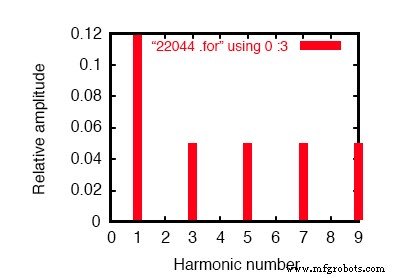
Gráfico SPICE de Fourier mostrando a fonte de 60 Hz e o 3º harmônico de 180 Hz.



Na análise de Fourier, (veja a figura acima e “Componentes de Fourier da resposta transitória v (2,3)”) as frequências mistas não são misturadas e são apresentadas separadamente.

Aqui vemos os mesmos 0,1198 amperes de corrente de 60 Hz (fundamental) que vimos na primeira simulação, mas aparecendo na 3ª linha harmônica vemos 49,9 mA:nossa fonte de corrente de 50 mA, 180 Hz em funcionamento. Por que não vemos todos os 50 mA na linha?

Como essa fonte de corrente está conectada ao resistor de carga de 1 kΩ, algumas de suas correntes são desviadas pela carga e nunca passam pela linha de volta à fonte. É uma consequência inevitável deste tipo de simulação, onde uma parte da carga é "normal" (um resistor) e a outra parte é imitada por uma fonte de corrente.

Simulação de sistema CA monofásico não linear com múltiplas fontes de corrente

Se adicionássemos mais fontes de corrente à "carga", veríamos uma distorção adicional da forma de onda da corrente de linha da forma de onda senoidal ideal, e cada uma dessas correntes harmônicas apareceria na análise de Fourier. Veja a figura abaixo e a listagem SPICE:“Simulação de carga não linear”.

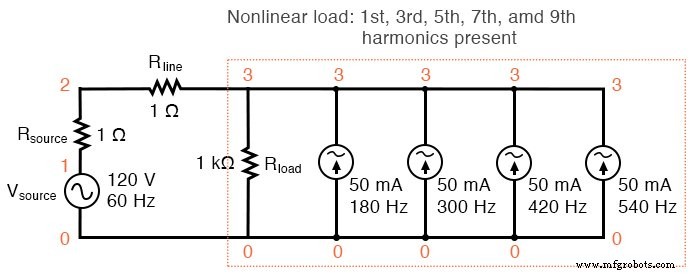
Carga não linear:1º, 3º, 5º, 7º e 9º harmônicos presentes.

 Simulação de carga não linear vsource 1 0 sin (0 120 60 0 0) rsource 1 2 1 rline 2 3 1 rload 3 0 1k i3har 3 0 sin (0 50m 180 0 0) i5har 3 0 sin (0 50m 300 0 0) i7har 3 0 sin (0 50m 420 0 0) i9har 3 0 sin (0 50m 540 0 0) .options itl5 =0 .tran 0,5m 30m 0 1u .plot tran v (2,3) .quatro 60 v (2,3). fim 

 Componentes de Fourier da resposta transitória v (2,3) componente dc =6.299E-11 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 1.198E-01 1.000000 -72.000 0,000 2 1.200E + 02 1.900E-09 0.000000 -93.908 -21.908 3 1.800E + 02 4.990E-02 0.416667 144.000 216.000 4 2,400E + 02 5,469E-09 0,000000 -116,873 -44,873 5 3.000E + 02 4.990E-02 0.416667 0.000 72.000 6 3,600E + 02 6,271E-09 0,000000 85,062 157,062 7 4.200E + 02 4.990E-02 0.416666 -144.000 -72.000 8 4,800E + 02 2,742E-09 0,000000 -38,781 33,219 9 5,400E + 02 4,990E-02 0,416666 72.000 144.000 distorção harmônica total =83,333296 por cento 

Análise de Fourier:“Componentes de Fourier da resposta transitória v (2,3)”.



Como você pode ver na análise de Fourier (Figura acima), cada fonte de corrente harmônica é igualmente representada na corrente da linha, a 49,9 mA cada. Até agora, esta é apenas uma simulação de sistema de energia monofásica.

Simulação de sistema CA trifásico

As coisas ficam mais interessantes quando fazemos uma simulação trifásica. Duas análises de Fourier serão realizadas:uma para a tensão em um resistor de linha e uma para a tensão em um resistor de neutro.

Como antes, a leitura de tensões através de resistências fixas de 1 Ω cada fornece indicações diretas de corrente através desses resistores. Veja a figura abaixo e a lista de SPICE “Sistema Y-Y de fonte / carga de 4 fios com harmônicos”.

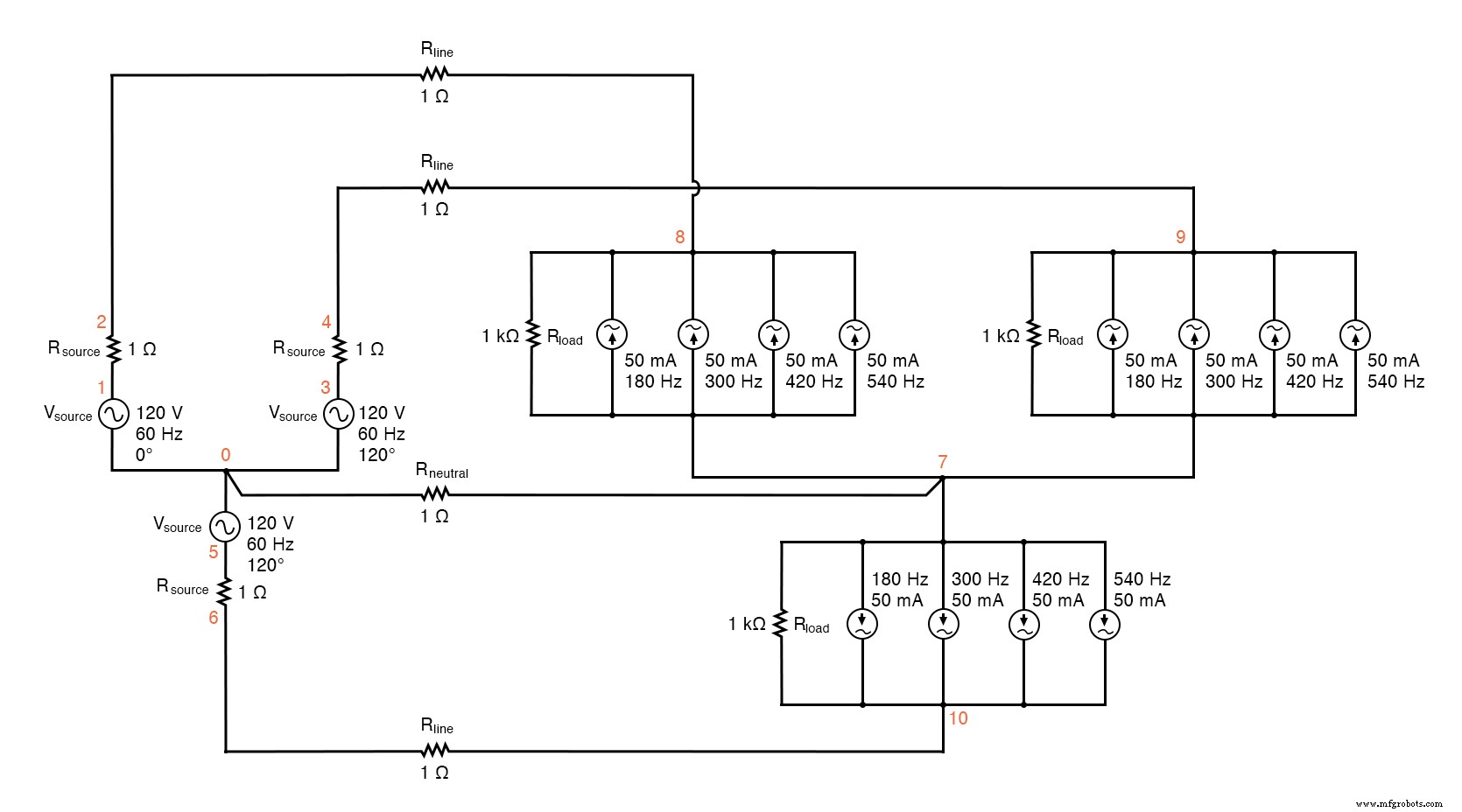
Circuito SPICE:análise de “corrente de linha” e “corrente neutra”, fonte Y-Y / sistema de carga de 4 fios com harmônicos.

 Fonte / carga Y-Y sistema de 4 fios com harmônicos * * fonte de tensão de fase 1 er (120 v / _ 0 graus) vsource1 1 0 sin (0 120 60 0 0) rsource1 1 2 1 * * fonte de tensão de fase 2 er (120 v / _ 120 graus) vsource2 3 0 sin (0 120 60 5.55555m 0) rsource2 3 4 1 * * fonte de tensão de fase 3 er (120 v / _ 240 graus) vsource3 5 0 sin (0 120 60 11.1111m 0) rsource3 5 6 1 * * resistências de fio neutro e de linha rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 rneutro 0 7 1 * * fase 1 de carga rload1 8 7 1k i3har1 8 7 sin (0 50m 180 0 0) i5har1 8 7 sin (0 50m 300 0 0) i7har1 8 7 sin (0 50m 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * fase 2 de carga rload2 9 7 1k i3har2 9 7 sin (0 50m 180 5.55555m 0) i5har2 9 7 sin (0 50m 300 5,55555m 0) i7har2 9 7 sin (0 50m 420 5.55555m 0) i9har2 9 7 sin (0 50m 540 5,555555m 0) * * fase 3 de carga rload3 10 7 1k i3har3 10 7 sin (0 50m 180 11.1111m 0) i5har3 10 7 sin (0 50m 300 11.1111m 0) i7har3 10 7 sin (0 50m 420 11.1111m 0) i9har3 10 7 sin (0 50m 540 11.1111m 0) * * material de análise .options itl5 =0 .tran 0,5m 100m 12m 1u .plot tran v (2,8) .quatro 60 v (2,8) .plot tran v (0,7) .quatro 60 v (0,7) .fim 

Análise de Fourier da corrente de linha:

 Componentes de Fourier da resposta transitória v (2,8) componente dc =-6.404E-12 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6,000E + 01 1,198E-01 1,000000 0,000 0,000 2 1.200E + 02 2.218E-10 0,000000 172,985 172,985 3 1.800E + 02 4.975E-02 0.415423 0.000 0.000 4 2,400E + 02 4,236E-10 0,000000 166,990 166,990 5 3,000E + 02 4,990E-02 0,416667 0,000 0,000 6 3,600E + 02 1,877E-10 0,000000 -147,146 -147,146 7 4,200E + 02 4,990E-02 0,416666 0,000 0,000 8 4.800E + 02 2.784E-10 0.000000 -148.811 -148.811 9 5,400E + 02 4,975E-02 0,415422 0,000 0,000 distorção harmônica total =83.209009 por cento 

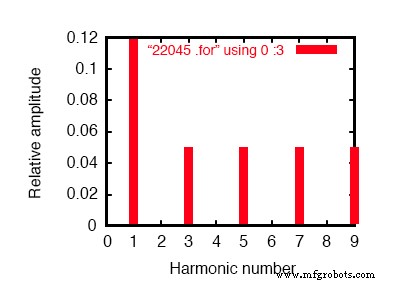
Análise de Fourier da corrente de linha no sistema Y-Y balanceado.

Análise de Fourier de corrente neutra:

 Componentes de Fourier da resposta transitória v (0,7) componente dc =1.819E-10 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 4.337E-07 1.000000 60.018 0,000 2 1.200E + 02 1.869E-10 0.000431 91.206 31.188 3 1.800E + 02 1.493E-01 344147.7638 -180.000 -240.018 4 2,400E + 02 1,257E-09 0,002898 -21,103 -81,121 5 3.000E + 02 9.023E-07 2.080596 119.981 59.963 6 3,600E + 02 3,396E-10 0,000783 15,882 -44,136 7 4,200E + 02 1,264E-06 2,913955 59,993 -0,025 8 4,800E + 02 5,975E-10 0,001378 35,584 -24,434 9 5.400E + 02 1.493E-01 344147.4889 -179.999 -240.017 

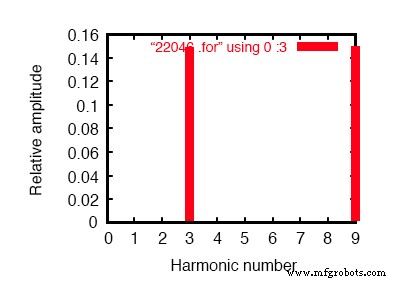
A análise de Fourier da corrente neutra mostra outra coisa além da ausência de harmônicos! Compare com a corrente de linha na figura acima.



Este é um sistema de energia Y-Y balanceado, cada fase idêntica ao sistema CA monofásico simulado anteriormente. Consequentemente, não deve ser surpresa que a análise de Fourier para corrente de linha em uma fase do sistema trifásico é quase idêntica à análise de Fourier para corrente de linha no sistema monofásico:uma corrente de linha fundamental (60 Hz) de 0,1198 amperes e correntes harmônicas ímpares de aproximadamente 50 mA cada.

Veja a figura acima e a análise de Fourier:“Componentes de Fourier da resposta transitória v (2,8)”

O que deveria ser surpreendente aqui é a análise da corrente do condutor neutro, conforme determinado pela queda de tensão em R _neutro resistor entre os nós SPICE 0 e 7.

Em uma carga Y trifásica balanceada, esperaríamos que a corrente de neutro fosse zero. Cada corrente de fase - que por si mesma passaria pelo fio neutro de volta para a fase de alimentação na fonte Y - deve cancelar uma a outra em relação ao condutor neutro porque todas são da mesma magnitude e todas deslocadas 120 °.

Em um sistema sem correntes harmônicas, isso é o que acontece, deixando zero de corrente pelo condutor neutro.

Efeitos das correntes harmônicas no sistema

No entanto, não podemos dizer o mesmo para harmônico correntes no mesmo sistema.

Observe que a corrente da frequência fundamental (60 Hz, ou 1º harmônico) está virtualmente ausente do condutor neutro. Nossa análise de Fourier mostra apenas 0,4337 µA do 1º harmônico ao ler a tensão em R _neutro . O mesmo pode ser dito sobre o 5º e o 7º harmônicos, ambas as correntes tendo magnitude desprezível.

Em contraste, o 3º e o 9º harmônicos são fortemente representados dentro do condutor neutro, com 149,3 mA (1,493E-01 volts em 1 Ω) cada! Isso é quase 150 mA, ou três vezes os valores das fontes de corrente, individualmente.

Com três fontes por frequência harmônica na carga, parece que nossas correntes de 3º e 9º harmônico em cada fase estão adicionando para formar a corrente neutra. Consulte a análise de Fourier:"Componentes de Fourier da resposta transitória v (0,7)"

Análise de gráfico no domínio do tempo

Isso é exatamente o que está acontecendo, embora possa não ser aparente por que isso acontece.

A chave para entender isso fica clara em um gráfico de correntes de fase no domínio do tempo. Examine este gráfico de correntes de fase balanceadas ao longo do tempo, com uma sequência de fase de 1-2-3. (Figura abaixo)

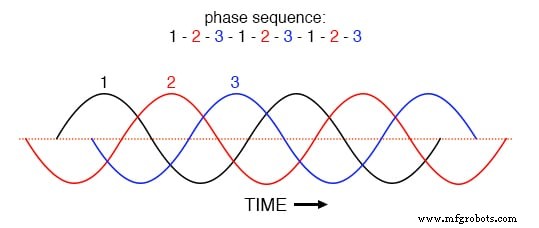
Sequência de fase 1-2-3-1-2-3-1-2-3 de ondas igualmente espaçadas.



Com as três formas de onda fundamentais igualmente deslocadas ao longo do eixo do tempo do gráfico, é fácil ver como elas se cancelariam para dar uma corrente resultante de zero no condutor neutro. Vamos considerar, no entanto, como seria uma forma de onda de 3º harmônico para a fase 1 sobreposta no gráfico da figura abaixo.

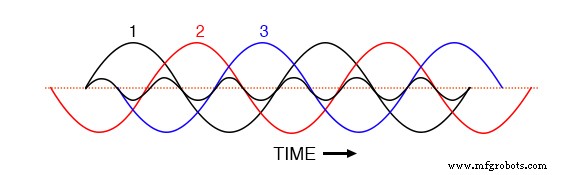
A forma de onda do terceiro harmônico para a fase 1 sobreposta a formas de onda fundamentais trifásicas.



Observe como esta forma de onda harmônica tem a mesma relação de fase com as 2ª e 3ª formas de onda fundamentais como tem com a 1ª:em cada semiciclo positivo de qualquer das formas de onda fundamentais, você encontrará exatamente dois meio-ciclos positivos e um meio-ciclo negativo da forma de onda harmônica.

O que isso significa é que as formas de onda de 3º harmônico de três formas de onda de frequência fundamental com deslocamento de fase de 120 ° estão na verdade em fase um com o outro. A figura de deslocamento de fase de 120 ° geralmente assumida em sistemas CA trifásicos se aplica apenas às frequências fundamentais, não aos seus múltiplos harmônicos!

Se tivéssemos que plotar todas as três formas de onda de 3ª harmônica no mesmo gráfico, veríamos elas se sobreporem com precisão e aparecerem como uma única forma de onda unificada (mostrada em negrito na (Figura abaixo)

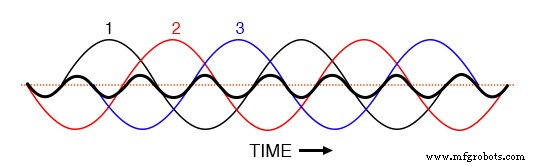
Os terceiros harmônicos para as fases 1, 2, 3 todos coincidem quando sobrepostos nas formas de onda trifásicas fundamentais.

Análise matemática do gráfico no domínio do tempo

Para os mais inclinados à matemática, esse princípio pode ser expresso simbolicamente. Suponha que A representa uma forma de onda e B outro, ambos na mesma frequência, mas deslocados 120 ° um do outro em termos de fase. Vamos chamar a 3ª harmônica de cada forma de onda de A ’ e B ’ , respectivamente.

A mudança de fase entre A ’ e B ’ não é 120 ° (que é a mudança de fase entre A e B ), mas 3 vezes isso, porque o A ’ e B ’ as formas de onda se alternam três vezes mais rápido que A e B . A mudança entre as formas de onda só é expressa com precisão em termos de ângulo de fase quando a mesma velocidade angular é assumida.

Ao relacionar formas de onda de diferentes frequências, a maneira mais precisa de representar a mudança de fase é em termos de tempo ; e o time-shift entre A ’ e B ’ é equivalente a 120 ° em uma frequência três vezes menor, ou 360 ° na frequência de A ' e B ’ . Uma mudança de fase de 360 ​​° é igual a uma mudança de fase de 0 °, ou seja, nenhuma mudança de fase.

Assim, A ’ e B ’ devem estar em fase um com o outro:







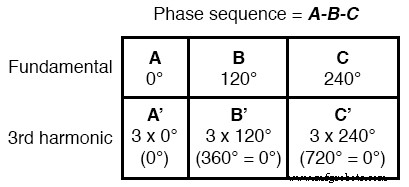
Esta característica do 3º harmônico em um sistema trifásico também é verdadeira para quaisquer múltiplos inteiros do 3º harmônico.

Portanto, não apenas as formas de onda do 3º harmônico de cada forma de onda fundamental estão em fase entre si, mas também o 6º harmônico, o 9º harmônico, o 12º harmônico, o 15º harmônico, o 18º harmônico, o 21º harmônico e assim por diante.

Uma vez que apenas harmônicos ímpares aparecem em sistemas onde a distorção da forma de onda é simétrica em relação à linha central - e a maioria das cargas não lineares criam distorção simétrica - múltiplos pares do 3º harmônico (6º, 12º, 18º, etc.) geralmente não são significativos, deixando apenas o múltiplos ímpares (3º, 9º, 15º, 21º, etc.) para contribuir significativamente para as correntes neutras.

Em sistemas de potência polifásicos com algum número de fases diferente de três, esse efeito ocorre com harmônicos do mesmo múltiplo. Por exemplo, as correntes harmônicas que adicionam o condutor neutro de um sistema de 4 fases conectado em estrela, onde a mudança de fase entre as formas de onda fundamentais é 90 °, seriam 4, 8, 12, 16, 20 e assim por diante.

Harmônicos Triplen

Devido à sua abundância e importância em sistemas de potência trifásicos, o 3º harmônico e seus múltiplos têm seu próprio nome especial: harmônicos triplos .

Todas as harmônicas triplas adicionam-se umas às outras no condutor neutro de uma carga conectada em Y de 4 fios. Em sistemas de energia contendo carga não linear substancial, as correntes harmônicas triplas podem ser de magnitude grande o suficiente para causar superaquecimento nos condutores neutros.

Isso é muito problemático, pois outras questões de segurança proíbem os condutores neutros de ter proteção de sobrecorrente e, portanto, não há provisão para interrupção automática dessas altas correntes.

Análise dos efeitos de harmônicas triplas em um circuito Y-Y

A ilustração a seguir mostra como as correntes harmônicas triplas criadas na carga se somam ao condutor neutro. O símbolo “ω” é usado para representar a velocidade angular e é matematicamente equivalente a 2πf. Portanto, “ω” representa a frequência fundamental, “3ω” representa o 3º harmônico, “5ω” representa o 5º harmônico e assim por diante:(Figura abaixo)





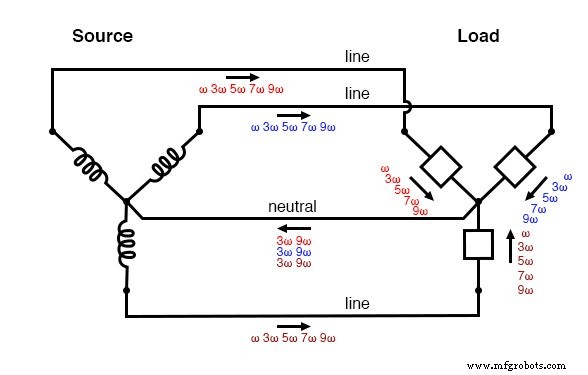
Fonte / carga triplen “Y-Y”:correntes harmônicas adicionam condutor neutro.



Em um esforço para mitigar essas correntes triplas aditivas, pode-se ficar tentado a remover o fio neutro inteiramente. Se não houver um fio neutro no qual as correntes triplas possam fluir juntas, então elas não funcionarão, certo?

Infelizmente, fazer isso apenas causa um problema diferente:o ponto central "Y" da carga não estará mais com o mesmo potencial da fonte, o que significa que cada fase da carga receberá uma tensão diferente daquela produzida pela fonte.

Vamos executar novamente a última simulação SPICE sem o 1 Ω R _neutro resistor e veja o que acontece:

 Fonte / carga Y-Y (sem neutro) com harmônicos * * fonte de tensão de fase 1 er (120 v / 0 graus) vsource1 1 0 sin (0 120 60 0 0) rsource1 1 2 1 * * fonte de tensão de fase 2 er (120 v / 120 graus) vsource2 3 0 sin (0 120 60 5.55555m 0) rsource2 3 4 1 * * fonte de tensão de fase 3 er (120 v / 240 graus) vsource3 5 0 sin (0 120 60 11.1111m 0) rsource3 5 6 1 * * resistências de linha rline1 2 8 1 rline2 4 9 1 rline3 6 10 1 * * fase 1 de carga rload1 8 7 1k i3har1 8 7 sin (0 50m 180 0 0) i5har1 8 7 sin (0 50m 300 0 0) i7har1 8 7 sin (0 50m 420 0 0) i9har1 8 7 sin (0 50m 540 0 0) * * fase 2 de carga rload2 9 7 1k i3har2 9 7 sin (0 50m 180 5.55555m 0) i5har2 9 7 sin (0 50m 300 5,55555m 0) i7har2 9 7 sin (0 50m 420 5.55555m 0) i9har2 9 7 sin (0 50m 540 5,555555m 0) * * fase 3 de carga rload3 10 7 1k i3har3 10 7 sin (0 50m 180 11.1111m 0) i5har3 10 7 sin (0 50m 300 11.1111m 0) i7har3 10 7 sin (0 50m 420 11.1111m 0) i9har3 10 7 sin (0 50m 540 11.1111m 0) * * material de análise .options itl5 =0 .tran 0,5m 100m 12m 1u .plot tran v (2,8) .quatro 60 v (2,8) .plot tran v (0,7) .quatro 60 v (0,7) .plot tran v (8,7) .quatro 60 v (8,7) .fim 

Análise de Fourier da corrente de linha:

 Componentes de Fourier da resposta transitória v (2,8) componente dc =5,423E-11 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6,000E + 01 1,198E-01 1,000000 0,000 0,000 2 1.200E + 02 2.388E-10 0,000000 158,016 158,016 3 1.800E + 02 3.136E-07 0,000003 -90,009 -90,009 4 2,400E + 02 5,963E-11 0,000000 -111,510 -111,510 5 3,000E + 02 4,990E-02 0,416665 0,000 0,000 6 3,600E + 02 8,606E-11 0,000000 -124,565 -124,565 7 4,200E + 02 4,990E-02 0,416668 0,000 0,000 8 4,800E + 02 8,126E-11 0,000000 -159,638 -159,638 9 5,400E + 02 9,406E-07 0,000008 -90,005 -90,005 distorção harmônica total =58,925539 por cento 

Análise de Fourier da tensão entre os dois pontos centrais “Y”:

 Componentes de Fourier da resposta transitória v (0,7) componente dc =6.093E-08 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6.000E + 01 1.453E-04 1.000000 60.018 0,000 2 1.200E + 02 6.263E-08 0.000431 91.206 31.188 3 1.800E + 02 5.000E + 01 344147.7879 -180.000 -240.018 4 2.400E + 02 4.210E-07 0,002898 -21,103 -81,121 5 3.000E + 02 3.023E-04 2.080596 119.981 59.963 6 3,600E + 02 1,138E-07 0,000783 15,882 -44,136 7 4,200E + 02 4,234E-04 2,913955 59,993 -0,025 8 4,800E + 02 2.001E-07 0,001378 35,584 -24,434 9 5,400E + 02 5,000E + 01 344147,4728 -179,999 -240,017 distorção harmônica total =************ por cento 

Análise de Fourier da tensão da fase de carga:

 Componentes de Fourier da resposta transitória v (8,7) componente dc =6.070E-08 frequência harmônica Fourier normalizada fase normalizada nenhum componente (hz) componente (deg) fase (deg) 1 6,000E + 01 1,198E + 02 1,000000 0,000 0,000 2 1.200E + 02 6.231E-08 0.000000 90.473 90.473 3 1.800E + 02 5.000E + 01 0.417500 -180.000 -180.000 4 2,400E + 02 4,278E-07 0,000000 -19,747 -19,747 5 3.000E + 02 9.995E-02 0.000835 179.850 179.850 6 3,600E + 02 1,023E-07 0,000000 13,485 13,485 7 4,200E + 02 9,959E-02 0,000832 179,790 179,789 8 4,800E + 02 1.991E-07 0,000000 35,462 35,462 9 5,400E + 02 5,000E + 01 0,417499 -179,999 -179,999 distorção harmônica total =59,043467 por cento 

Coisas estranhas estão acontecendo, de fato.

Primeiro, vemos que as correntes harmônicas triplas (3ª e 9ª) quase desaparecem nas linhas que conectam uma carga à fonte. As correntes de 5ª e 7ª harmônicas estão presentes em seus níveis normais (aproximadamente 50 mA), mas as correntes de 3ª e 9ª harmônicas são de magnitude desprezível.

Em segundo lugar, vemos que há uma tensão harmônica substancial entre os dois pontos centrais “Y”, entre os quais o condutor neutro costumava se conectar. De acordo com o SPICE, há 50 volts de frequência de 3º e 9º harmônicos entre esses dois pontos, o que definitivamente não é normal em um sistema Y linear (sem harmônicos) equilibrado.

Finalmente, a tensão medida em uma das fases da carga (entre os nós 8 e 7 na análise SPICE) da mesma forma mostra fortes tensões harmônicas triplen de 50 volts cada.

A figura abaixo é um resumo gráfico dos efeitos mencionados.





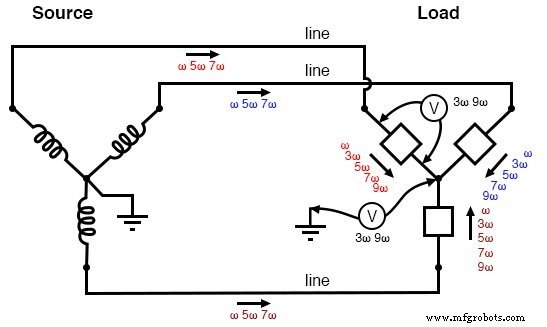
Sistema de três fios “Y-Y” (sem neutro):tensões triplen aparecem entre os centros “Y”. Tensões triplas aparecem nas fases de carga. Correntes não triplicadas aparecem nos condutores de linha.



Em resumo, a remoção do condutor neutro leva a um ponto central “quente” na carga “Y” e também a tensões de fase de carga harmônica de igual magnitude, todas compostas por frequências triplas.

Na simulação anterior, onde tínhamos um sistema conectado em Y de 4 fios, o efeito indesejável dos harmônicos era corrente de neutro excessivo , mas pelo menos cada fase da carga recebeu tensão quase livre de harmônicos.

Análise dos efeitos de harmônicas triplas em um circuito Delta-Wye (Y)

Uma vez que a remoção do fio neutro não pareceu funcionar na eliminação dos problemas causados ​​por harmônicos, talvez mudar para uma configuração Δ funcione. Vamos tentar uma fonte Δ em vez de um Y, mantendo a carga em sua configuração Y atual e ver o que acontece.

Os parâmetros medidos serão a corrente de linha (tensão em R _linha , nós 0 e 8), tensão de fase de carga (nós 8 e 7) e corrente de fase de fonte (tensão em R _fonte , nós 1 e 2). (Figura abaixo)

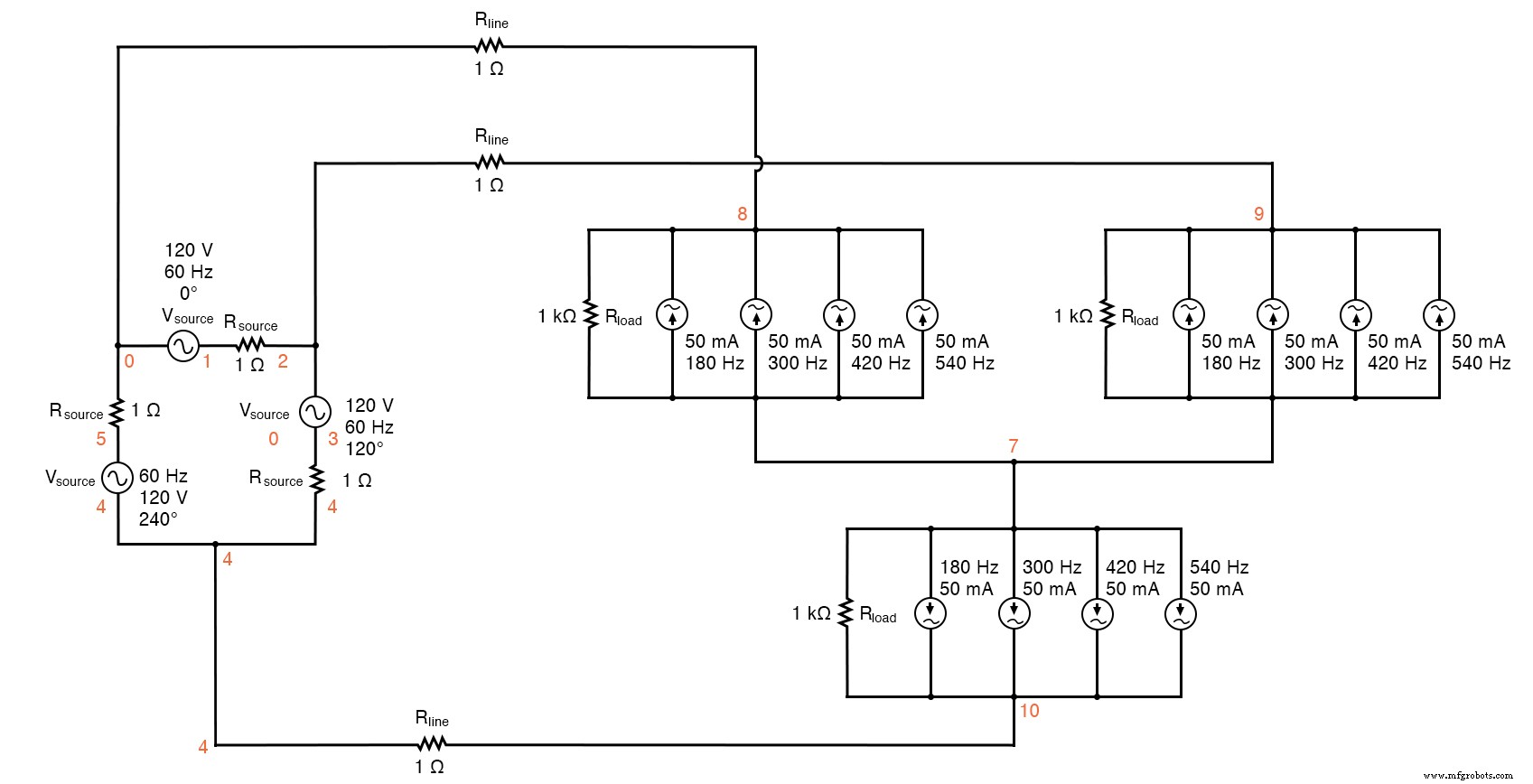
Fonte / carga Delta-Y com harmônicos

 Fonte / carga Delta-Y com harmônicos * * fonte de tensão de fase 1 er (120 v / _ 0 graus) vsource1 1 0 sin (0 207,846 60 0 0) rsource1 1 2 1 * * fonte de tensão de fase 2 er (120 v / _ 120 graus) vsource2 3 2 sin (0 207,846 60 5,555555m 0) rsource2 3 4 1 * * fonte de tensão de fase 3 er (120 v / _ 240 graus) vsource3 5 4 sin (0 207.846 60 11.1111m 0) rsource3 5 0 1 * * resistências de linha rline1 0 8 1 rline2 2 9 1 rline3 4 10 1 * * fase 1 de carga rload1 8 7 1k i3har1 8 7 sin (0 50m 180 9.72222m 0) i5har1 8 7 sin (0 50m 300 9,72222m 0) i7har1 8 7 sin (0 50m 420 9,72222m 0) i9har1 8 7 sin (0 50m 540 9,72222m 0) * * fase 2 de carga rload2 9 7 1k i3har2 9 7 sin (0 50m 180 15,2777m 0) i5har2 9 7 sin (0 50m 300 15,2777m 0) i7har2 9 7 sin (0 50m 420 15,2777m 0) i9har2 9 7 sin (0 50m 540 15,2777m 0) * * fase 3 de carga rload3 10 7 1k i3har3 10 7 sin (0 50m 180 4.16666m 0) i5har3 10 7 sin (0 50m 300 4.16666m 0) i7har3 10 7 sin (0 50m 420 4,166666m 0) i9har3 10 7 sin (0 50m 540 4,166666m 0) * * material de análise .options itl5 =0 .tran 0,5m 100m 16m 1u .plotar tran v (0,8) v (8,7) v (1,2) .quatro 60 v (0,8) v (8,7) v (1,2) .fim 

Nota:o parágrafo seguinte é para aqueles leitores curiosos que seguem todos os detalhes das minhas netlists SPICE. Se você quer apenas saber o que acontece no circuito, pule este parágrafo!

Ao simular circuitos com fontes CA de frequência e fase diferentes, a única maneira de fazer isso no SPICE é configurar as fontes com um tempo de atraso ou deslocamento de fase especificado em segundos. Assim, a fonte de 0 ° tem estes cinco números de especificação:"(0 207,846 60 0 0)", o que significa 0 volts DC offset, 207,846 volts de amplitude de pico (120 vezes a raiz quadrada de três, para garantir que as tensões de fase de carga permaneçam em 120 volts cada), 60 Hz, 0 atraso de tempo e 0 fator de amortecimento.

A fonte com mudança de fase de 120 ° tem estes números:"(0 207,846 60 5,555555m 0)", todos iguais à primeira, exceto para o fator de atraso de 5,55555 milissegundos, ou 1/3 do período completo de 16,6667 milissegundos para uma forma de onda de 60 Hz.

The 240° source must be time-delayed twice that amount, equivalent to a fraction of 240/360 of 16.6667 milliseconds, or 11.1111 milliseconds.

This is for the Δ-connected source. The Y-connected load, on the other hand, requires a different set of time-delay figures for its harmonic current sources, because the phase voltages in a Y load are not in phase with the phase voltages of a Δ source.

If Δ source voltages VAC, VBA, and VCB are referenced at 0°, 120°, and 240°, respectively, then “Y” load voltages VA, VB, and VC will have phase angles of -30°, 90°, and 210°, respectively.

This is an intrinsic property of all Δ-Y circuits and not a quirk of SPICE. Therefore, when I specified the delay times for the harmonic sources, I had to set them at 15.2777 milliseconds (-30°, or +330°), 4.16666 milliseconds (90°), and 9.72222 milliseconds (210°).

One final note:when delaying AC sources in SPICE, they don’t “turn on” until their delay time has elapsed, which means any mathematical analysis up to that point in time will be in error. Consequently, I set the .tran transient analysis line to hold off analysis until 16 milliseconds after the start, which gives all sources in the netlist time to engage before any analysis takes place.

The result of this analysis is almost as disappointing as the last. (Figure below) Line currents remain unchanged (the only substantial harmonic content being the 5th and 7th harmonics), and load phase voltages remain unchanged as well, with a full 50 volts of triplen harmonic (3rd and 9th) frequencies across each load component.

Source phase current is a fraction of the line current, which should come as no surprise. Both 5th and 7th harmonics are represented there, with negligible triplen harmonics:

Fourier analysis of line current:

 Fourier components of transient response v(0,8) dc component =-6.850E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E-01 1.000000 150.000 0.000 2 1.200E+02 2.491E-11 0.000000 159.723 9.722 3 1.800E+02 1.506E-06 0.000013 0.005 -149.996 4 2.400E+02 2.033E-11 0.000000 52.772 -97.228 5 3.000E+02 4.994E-02 0.416682 30.002 -119.998 6 3.600E+02 1.234E-11 0.000000 57.802 -92.198 7 4.200E+02 4.993E-02 0.416644 -29.998 -179.998 8 4.800E+02 8.024E-11 0.000000 -174.200 -324.200 9 5.400E+02 4.518E-06 0.000038 -179.995 -329.995 total harmonic distortion =58.925038 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(8,7) dc component =1.259E-08 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.198E+02 1.000000 150.000 0.000 2 1.200E+02 1.941E-07 0.000000 49.693 -100.307 3 1.800E+02 5.000E+01 0.417222 -89.998 -239.998 4 2.400E+02 1.519E-07 0.000000 66.397 -83.603 5 3.000E+02 6.466E-02 0.000540 -151.112 -301.112 6 3.600E+02 2.433E-07 0.000000 68.162 -81.838 7 4.200E+02 6.931E-02 0.000578 148.548 -1.453 8 4.800E+02 2.398E-07 0.000000 -174.897 -324.897 9 5.400E+02 5.000E+01 0.417221 90.006 -59.995 total harmonic distortion =59.004109 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(1,2) dc component =3.564E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 6.906E-02 1.000000 -0.181 0.000 2 1.200E+02 1.525E-11 0.000000 -156.674 -156.493 3 1.800E+02 1.422E-06 0.000021 -179.996 -179.815 4 2.400E+02 2.949E-11 0.000000 -110.570 -110.390 5 3.000E+02 2.883E-02 0.417440 -179.996 -179.815 6 3.600E+02 2.324E-11 0.000000 -91.926 -91.745 7 4.200E+02 2.883E-02 0.417398 -179.994 -179.813 8 4.800E+02 4.140E-11 0.000000 -39.875 -39.694 9 5.400E+02 4.267E-06 0.000062 0.006 0.186 total harmonic distortion =59.031969 percent 

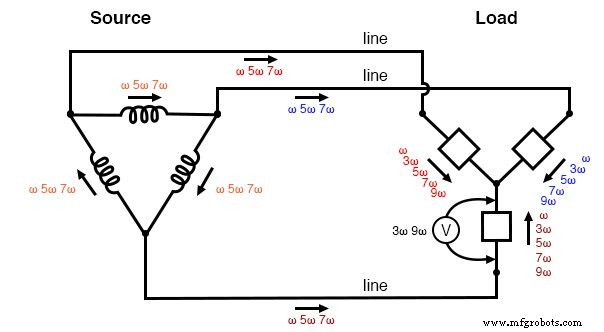
“Δ-Y” source/load:Triplen voltages appear across load phases. Non-triplen currents appear in line conductors and in source phase windings.



Really, the only advantage of the Δ-Y configuration from the standpoint of harmonics is that there is no longer a center-point at the load posing a shock hazard. Otherwise, the load components receive the same harmonically-rich voltages and the lines see the same currents as in a three-wire Y system.

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

If we were to reconfigure the system into a Δ-Δ arrangement, (Figure below) that should guarantee that each load component receives non-harmonic voltage, since each load phase would be directly connected in parallel with each source phase.

The complete lack of any neutral wires or “center points” in a Δ-Δ system prevents strange voltages or additive currents from occurring.

It would seem to be the ideal solution. Let’s simulate and observe, analyzing line current, load phase voltage, and source phase current. See SPICE listing:“Delta-Delta source/load with harmonics”, “Fourier analysis:Fourier components of transient response v(0,6)”, and “Fourier components of transient response v(2,1)”.

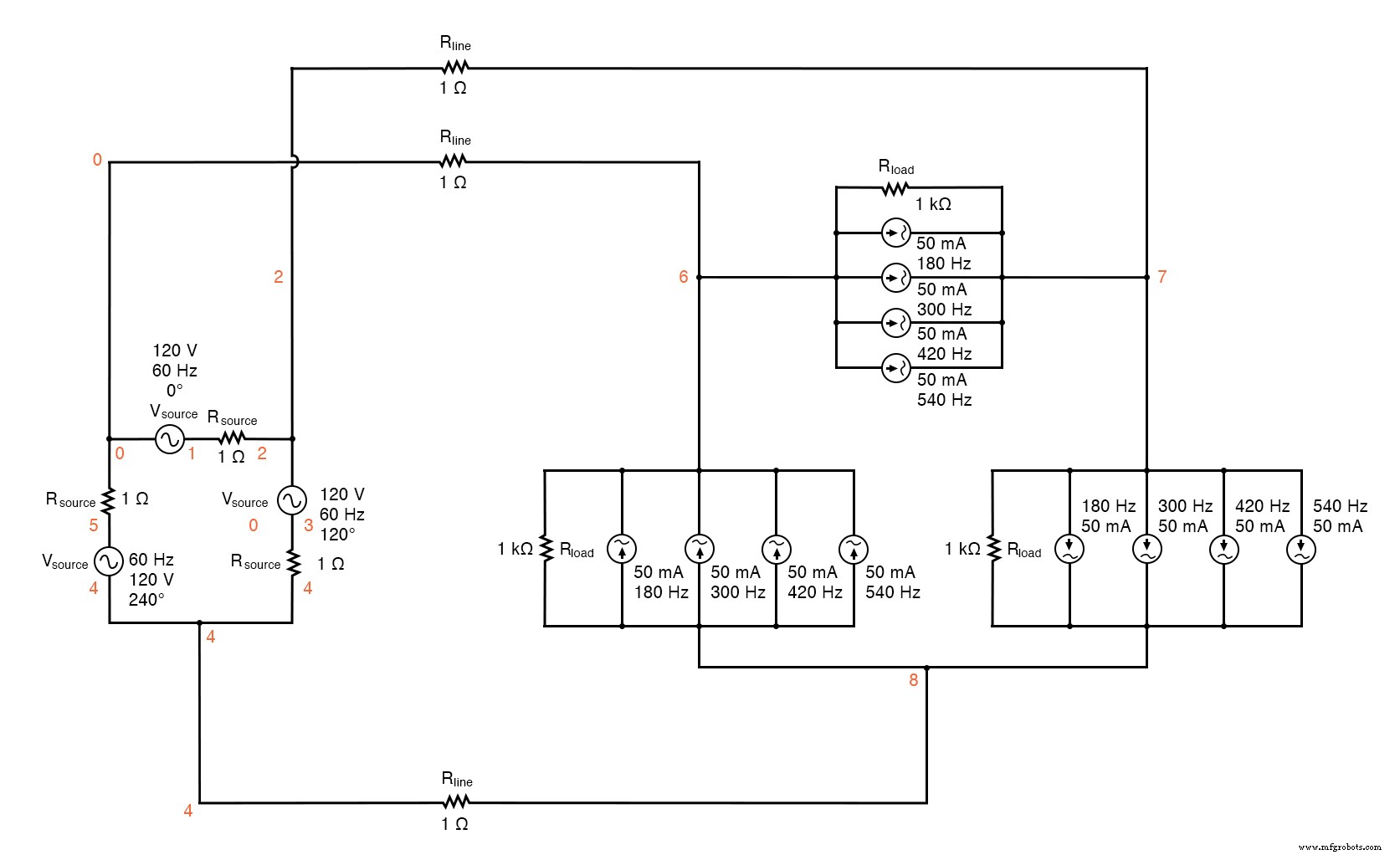
Delta-Delta source/load with harmonics.

Delta-Delta source/load with harmonics * * phase1 voltage source and r (120 v /_ 0 deg) vsource1 1 0 sin(0 120 60 0 0) rsource1 1 2 1 * * phase2 voltage source and r (120 v /_ 120 deg) vsource2 3 2 sin(0 120 60 5.55555m 0) rsource2 3 4 1 * * phase3 voltage source and r (120 v /_ 240 deg) vsource3 5 4 sin(0 120 60 11.1111m 0) rsource3 5 0 1 * * line resistances rline1 0 6 1 rline2 2 7 1 rline3 4 8 1 * * phase 1 of load rload1 7 6 1k i3har1 7 6 sin(0 50m 180 0 0) i5har1 7 6 sin(0 50m 300 0 0) i7har1 7 6 sin(0 50m 420 0 0) i9har1 7 6 sin(0 50m 540 0 0) * * phase 2 of load rload2 8 7 1k i3har2 8 7 sin(0 50m 180 5.55555m 0) i5har2 8 7 sin(0 50m 300 5.55555m 0) i7har2 8 7 sin(0 50m 420 5.55555m 0) i9har2 8 7 sin(0 50m 540 5.55555m 0) * * phase 3 of load rload3 6 8 1k i3har3 6 8 sin(0 50m 180 11.1111m 0) i5har3 6 8 sin(0 50m 300 11.1111m 0) i7har3 6 8 sin(0 50m 420 11.1111m 0) i9har3 6 8 sin(0 50m 540 11.1111m 0) * * analysis stuff .options itl5=0 .tran 0.5m 100m 16m 1u .plot tran v(0,6) v(7,6) v(2,1) i(3har1) .four 60 v(0,6) v(7,6) v(2,1) .fim 

Fourier analysis of line current:

Fourier components of transient response v(0,6) dc component =-6.007E-11 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 2.070E-01 1.000000 150.000 0.000 2 1.200E+02 5.480E-11 0.000000 156.666 6.666 3 1.800E+02 6.257E-07 0.000003 89.990 -60.010 4 2.400E+02 4.911E-11 0.000000 8.187 -141.813 5 3.000E+02 8.626E-02 0.416664 -149.999 -300.000 6 3.600E+02 1.089E-10 0.000000 -31.997 -181.997 7 4.200E+02 8.626E-02 0.416669 150.001 0.001 8 4.800E+02 1.578E-10 0.000000 -63.940 -213.940 9 5.400E+02 1.877E-06 0.000009 89.987 -60.013 total harmonic distortion =58.925538 percent 

Fourier analysis of load phase voltage:

Fourier components of transient response v(7,6) dc component =-5.680E-10 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.195E+02 1.000000 0.000 0.000 2 1.200E+02 1.039E-09 0.000000 144.749 144.749 3 1.800E+02 1.251E-06 0.000000 89.974 89.974 4 2.400E+02 4.215E-10 0.000000 36.127 36.127 5 3.000E+02 1.992E-01 0.001667 -180.000 -180.000 6 3.600E+02 2.499E-09 0.000000 -4.760 -4.760 7 4.200E+02 1.992E-01 0.001667 -180.000 -180.000 8 4.800E+02 2.951E-09 0.000000 -151.385 -151.385 9 5.400E+02 3.752E-06 0.000000 89.905 89.905 total harmonic distortion =0.235702 percent 

Fourier analysis of source phase current:

Fourier components of transient response v(2,1) dc component =-1.923E-12 harmonic frequency Fourier normalized phase normalized no (hz) component component (deg) phase (deg) 1 6.000E+01 1.194E-01 1.000000 179.940 0.000 2 1.200E+02 2.569E-11 0.000000 133.491 -46.449 3 1.800E+02 3.129E-07 0.000003 89.985 -89.955 4 2.400E+02 2.657E-11 0.000000 23.368 -156.571 5 3.000E+02 4.980E-02 0.416918 -180.000 -359.939 6 3.600E+02 4.595E-11 0.000000 -22.475 -202.415 7 4.200E+02 4.980E-02 0.416921 -180.000 -359.939 8 4.800E+02 7.385E-11 0.000000 -63.759 -243.699 9 5.400E+02 9.385E-07 0.000008 89.991 -89.949 total harmonic distortion =58.961298 percent 

As predicted earlier, the load phase voltage is almost a pure sine-wave, with negligible harmonic content, thanks to the direct connection with the source phases in a Δ-Δ system.

But what happened to the triplen harmonics? The 3rd and 9th harmonic frequencies don’t appear in any substantial amount in the line current, nor in the load phase voltage, nor in the source phase current! We know that triplen currents exist because the 3rd and 9th harmonic current sources are intentionally placed in the phases of the load, but where did those currents go?

Analysis of the Effects of Triplen Harmonics in a Delta - Delta Circuit

Remember that the triplen harmonics of 120° phase-shifted fundamental frequencies are in phase with each other.

Note the directions that the arrows of the current sources within the load phases are pointing, and think about what would happen if the 3rd and 9th harmonic sources were DC sources instead.

What we would have is currently circulating within the loop formed by the Δ-connected phases . This is where the triplen harmonic currents have gone:they stay within the Δ of the load, never reaching the line conductors or the windings of the source.

These results may be graphically summarized as such in the figure below.

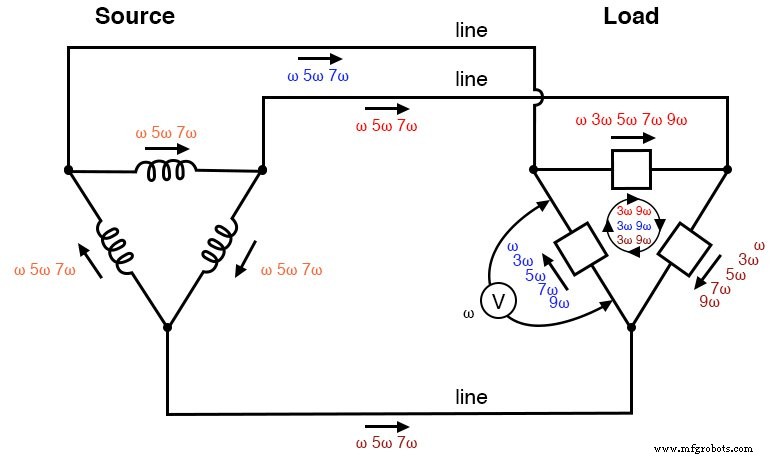
Δ-Δ source/load:Load phases receive undistorted sine wave voltages. Triplen currents are confined to circulate within load phases. Non-triplen currents appear in line conductors and in source phase windings.



This is a major benefit of the Δ-Δ system configuration:triplen harmonic currents remain confined in whatever set of components create them and do not “spread” to other parts of the system.



REVER:

• Nonlinear components are those that draw a non-sinusoidal (non-sine-wave) current waveform when energized by a sinusoidal (sine-wave) voltage. Since any distortion of an originally pure sine-wave constitutes harmonic frequencies, we can say that nonlinear components generate harmonic currents.
• When the sine-wave distortion is symmetrical above and below the average centerline of the waveform, the only harmonics present will be odd-numbered , not even-numbered.
• The 3rd harmonic, and integer multiples of it (6th, 9th, 12th, 15th) are known as triplen harmonics. They are in phase with each other, despite the fact that their respective fundamental waveforms are 120° out of phase with each other.
• In a 4-wire Y-Y system, triplen harmonic currents add within the neutral conductor.
• Triplen harmonic currents in a Δ-connected set of components circulate within the loop formed by the Δ.

PLANILHAS RELACIONADAS:

• Mixed-Frequency Signals Worksheet