Computando transformadas rápidas de Fourier no MCU LPC55S69

Este artigo investiga o Transform Engine, outra parte do PowerQuad, que permite que o MCU LPC55S69 calcule uma Fast Fourier Transform (FFT).

O microcontrolador LPC55S69 da NXP contém muitos recursos que o tornam adequado para uma variedade de aplicações. O MCU LPC55S69 e sua unidade PowerQuad incluem componentes exclusivos - o Biquad e os Transform Engines - que são usados ​​para completar várias tarefas, deixando os principais núcleos da CPU livres para outras coisas.

Um artigo anterior, Understanding Digital Filtering with Embedded Microcontrollers, explorou vários métodos amplamente usados ​​para filtrar e processar amostras de dados no domínio do tempo. Para isso, utilizou o motor Biquad da unidade PowerQuad do LPC55S69.

Este artigo investiga o Transform Engine, outra parte do PowerQuad, que permite que o LPC55S69 MCU calcule uma Fast Fourier Transform (FFT).

Compreendendo as transformadas discretas de Fourier

Ao lidar com medições diárias, como comprimentos e temperaturas, existe um conjunto de ferramentas para determinar o tamanho e a temperatura da coisa particular que está sendo medida. Para sinais no domínio do tempo, a escolha da ferramenta de medição pode não ser tão aparente. Considere o seguinte exemplo de sinal dado na Figura 1.

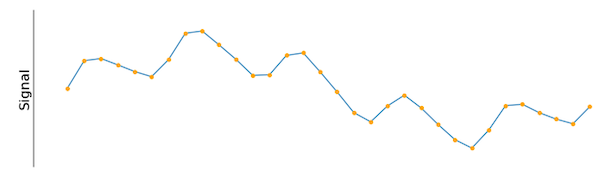
Figura 1. Um sinal de entrada amostrado em um intervalo constante.

Como esse sinal pode ser medido, compreendido e descrito? As escolhas possíveis podem ser a amplitude, a frequência ou vários valores calculados com métodos de estatísticas. Uma maneira de começar é medindo o sinal de interesse em relação a uma onda de cosseno conhecida, mostrada na Figura 2.

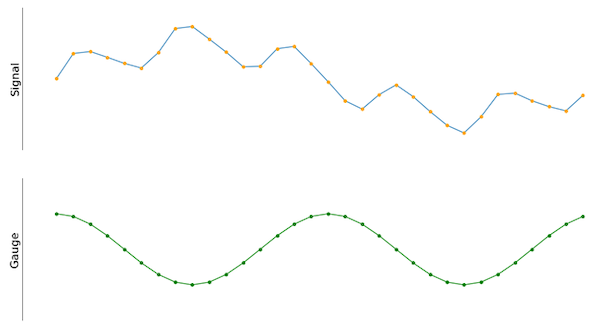
Figura 2. O sinal de entrada próximo a um sinal de medidor de cosseno. Ambos têm o mesmo número de amostras.

Como a amplitude e a frequência da onda do cosseno podem ser facilmente fixadas e, portanto, identificadas, é possível comparar a onda do cosseno com o sinal de entrada. Se feito corretamente, o valor resultante do produto escalar entre o sinal de entrada e a onda do cosseno quantifica o quanto o sinal de entrada se correlaciona com o medidor. Para isso, é razoável pensar na entrada e no medidor de sinal como matrizes de entrada discretas do mesmo comprimento, e torna-se fácil calcular o produto escalar.

O resultado é um escalar e sua magnitude é proporcional a quão bem o sinal de entrada se correlaciona com o sinal do medidor de cosseno. A operação de produto escalar se resume a muitas operações de multiplicação e adição - a mesma operação discutida em Compreendendo a filtragem digital com microcontroladores incorporados.

Este método produz bons resultados rapidamente. Há, entretanto, um caso particular que não funciona ao aplicar este método. Se o sinal de entrada for uma onda cosseno com a mesma frequência do medidor, mas com sua fase deslocada em 90 graus em relação ao medidor, a saída do método mencionado será zero. Por inspeção visual, parece que ainda há uma correlação entre o medidor e o sinal de entrada, mas há detalhes que precisamos considerar.

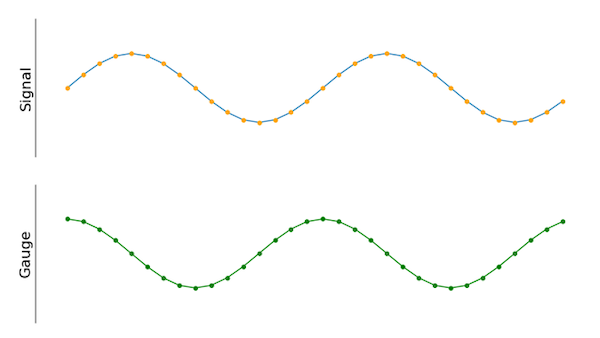
Figura 3. O novo sinal do medidor é alterado de fase em 90 graus em comparação com o antigo.

Esse comportamento pode ser comparado à medição do “comprimento” de uma tira fina de papel. Ao usar uma régua para determinar o comprimento de um lado da tira de papel, o papel pode ter 25 centímetros de comprimento e 2,5 centímetros de largura. Os dois números estão corretos, mas a régua teve que ser girada 90 graus para obter as duas medidas. Ambos os números estão tecnicamente corretos e podemos usá-los juntos para obter um verdadeiro “tamanho” (comprimento e largura) do nosso pedaço de papel. Para superar esse problema em termos de nosso sinal de entrada, um segundo medidor pode ser usado, como visto na Figura 4.

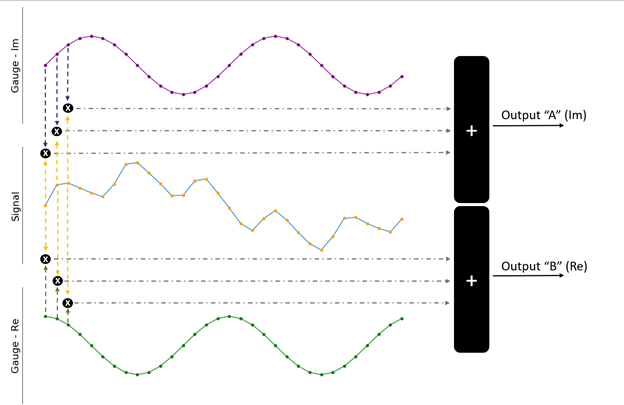
Figura 4. Ambos os sinais de medidor podem ser usados ​​para quantificar melhor o sinal de entrada.

A única diferença entre os dois medidores (mostrados em roxo e verde) é a mudança de fase de 90 graus. Na analogia anterior, isso equivale a girar a régua. O produto escalar é calculado entre o sinal de entrada e cada um dos medidores para obter a saída final. Isso produz resultados em dois valores A e B, cada um contendo o quão bem a entrada se correlaciona com um dos medidores. Normalmente, eles são considerados como um único número complexo:

output =B + i * A

A próxima etapa é comparar o sinal de entrada a uma gama de medidores com frequências diferentes (Figura 5).

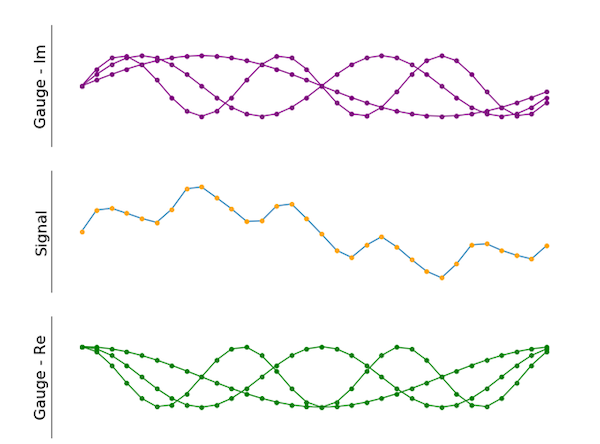
Figura 5. Vários medidores também podem ser aplicados. Os verdes são deslocados 90 graus em comparação com os roxos.

Como mostra a imagem, o resultado final incorpora alguns medidores diferentes. A parte imaginária (mostrada em roxo) é deslocada de fase em 90 graus em comparação com os sinais verdes (parte real), assim como no exemplo de dois medidores mostrado acima. Não há limite para o número de medidores diferentes.

O uso dessa técnica - chamada de Transformada Discreta de Fourier (DFT) - produz a geração de um espectro de saídas em todas as frequências de interesse para um problema. É possível definir a técnica matematicamente da seguinte forma:

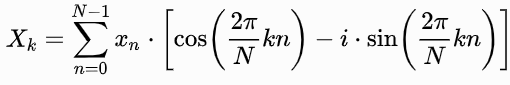
Equação 1. A descrição matemática do DFT.

Onde N é o número de amostras no sinal de entrada ek é a frequência dos medidores de referência (co) seno.

Limitações da transformação rápida de Fourier (FFT)

O FFT é uma forma numericamente eficiente de calcular o DFT que requer menos operações de multiplicação e adição em comparação com o método discutido acima. No entanto, existem algumas restrições à entrada:

1. O comprimento da entrada deve ser uma potência de dois.
2. Comprimentos de entrada arbitrários e espaçamento de frequência na saída não são permitidos. Os bins de saída são espaçados pela taxa de amostragem do sinal de entrada dividida pelo número de amostras na entrada. Se a entrada for, por exemplo, um sinal de 256 pontos amostrado em 48 kHz, as matrizes de saída correspondem a frequências espaçadas em 187 Hz (48.000 dividido por 256).
3. Quando a entrada consiste em números reais (por exemplo, amostras obtidas de um ADC), a saída é simétrica. Se a entrada, por exemplo, consistir em 64 amostras, o resultado FFT também consistirá em 64 números complexos. No entanto, a segunda metade da matriz de saída contém os conjugados complexos da primeira metade.

Usando o PowerQuad FFT Engine

A matemática por trás das operações DFT / FFT pode ser realizada por operações simples de multiplicação e adição, o que é ideal para terceirizar as operações matemáticas para um coprocessador dedicado, como o PowerQuad no LPC55S69 MCU. Por causa disso, os principais núcleos da CPU estão livres para trabalhar em outras tarefas.

Utilizar o mecanismo PowerQuad FFT é um processo simples, e o SDK oficial vem com projetos de exemplo que demonstram os recursos de coprocessamento. Um exemplo em particular, chamado powerquad_transform, demonstra o processo de cálculo FFT.

O arquivo powerquad_transform.c contém várias funções que testam os diferentes modos do mecanismo FFT. Um deles é a função PQ_RFFTFixed16Example. Este exemplo inicializa o PowerQuad para aceitar dados inteiros de 16 bits. Os dados de ponto flutuante devem ser convertidos em valores de ponto fixo com antecedência, pois o mecanismo de transformação PowerQuad só oferece suporte a inteiros.

FILTER_INPUT_LEN define o número de amostras de entrada. A matriz de saída tem o dobro do comprimento porque precisa armazenar as partes reais e imaginárias dos valores resultantes.

Figura 6. Esta parte do código define os dados de teste e os resultados esperados.

A última matriz contém dados de teste para verificar o resultado. Observe como a segunda metade da matriz contém os conjugados complexos conforme declarado acima. Além disso, os conjugados não são iguais (por exemplo, o par 76, -50 e 77,49). De qualquer forma, uma vez que os dados foram inicializados, a seguinte estrutura de dados é usada para configurar o PowerQuad:

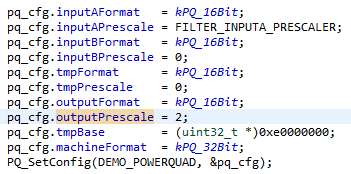
Figura 7. Esta parte do programa de exemplo configura e inicializa a unidade PowerQuad.

É necessário reduzir a escala da entrada para evitar que o algoritmo transborde. Esse processo acontece na segunda linha da imagem acima. FILTER_INPUTA_PRESCALER é definido como cinco porque existem 32 (dois elevado a potência de cinco) amostras. O pré-dimensionamento é outro recurso de hardware do PowerQuad, e provavelmente é o motivo da imprecisão observada nos resultados de teste esperados.

Depois que tudo estiver configurado, a localização das áreas de entrada e saída é passada para a unidade PowerQuad, o que acontece na função PQ_transformRFFT. Este método define alguns registros de configuração e inicia o PowerQuad gravando no registro de controle. Neste exemplo, a CPU espera que o PowerQuad termine. A espera nem sempre é necessária, e o PowerQuad pode realizar cálculos de forma assíncrona enquanto a CPU realiza outras tarefas.

Utilize o PowerQuad para operações matemáticas

O PowerQuad é um coprocessador para operações matemáticas complexas disponíveis em vários dispositivos da série LPC5500 MCU. Inclui um mecanismo especial para calcular FFTs com eficiência, o que pode ser feito independentemente dos núcleos principais da CPU. O SDK para o MCU LPC55S69 contém exemplos de como configurar e usar o PowerQuad.

A página da comunidade da NXP contém informações extensas, discussões e artigos centrados no MCU LPC55S69.

Artigos do setor são uma forma de conteúdo que permite aos parceiros do setor compartilhar notícias, mensagens e tecnologia úteis com os leitores do All About Circuits de uma forma que o conteúdo editorial não é adequado. Todos os artigos da indústria estão sujeitos a diretrizes editoriais rígidas com a intenção de oferecer aos leitores notícias úteis, conhecimentos técnicos ou histórias. Os pontos de vista e opiniões expressos nos Artigos da Indústria são do parceiro e não necessariamente da All About Circuits ou de seus redatores.