Como Usar um Exemplo de Rede Neural Perceptron Simples para Classificar Dados

Este artigo demonstra a funcionalidade básica de uma rede neural Perceptron e explica a finalidade do treinamento.

Este artigo faz parte de uma série sobre redes neurais Perceptron.

Se você gostaria de começar do início ou pular em frente, você pode verificar os outros artigos aqui:

1. Como realizar a classificação usando uma rede neural:o que é o Perceptron?
2. Como usar um exemplo de rede neural simples Perceptron para classificar dados
3. Como treinar uma rede neural Perceptron básica
4. Compreendendo o treinamento de rede neural simples
5. Uma introdução à teoria de treinamento para redes neurais
6. Compreendendo a taxa de aprendizagem em redes neurais
7. Aprendizado de máquina avançado com o Multilayer Perceptron
8. A função de ativação sigmóide:ativação em redes neurais multicamadas Perceptron
9. Como treinar uma rede neural multicamadas Perceptron
10. Noções básicas sobre fórmulas de treinamento e retropropagação para percepções multicamadas
11. Arquitetura de rede neural para uma implementação Python
12. Como criar uma rede neural multicamadas Perceptron em Python
13. Processamento de sinais usando redes neurais:validação no projeto de redes neurais
14. Conjuntos de dados de treinamento para redes neurais:como treinar e validar uma rede neural Python

O que é um Perceptron de camada única?

No artigo anterior, vimos que uma rede neural consiste em nós interconectados dispostos em camadas. Os nós na camada de entrada distribuem dados e os nós em outras camadas executam a soma e, em seguida, aplicam uma função de ativação. As conexões entre esses nós são ponderadas, o que significa que cada conexão multiplica o dado transferido por um valor escalar.

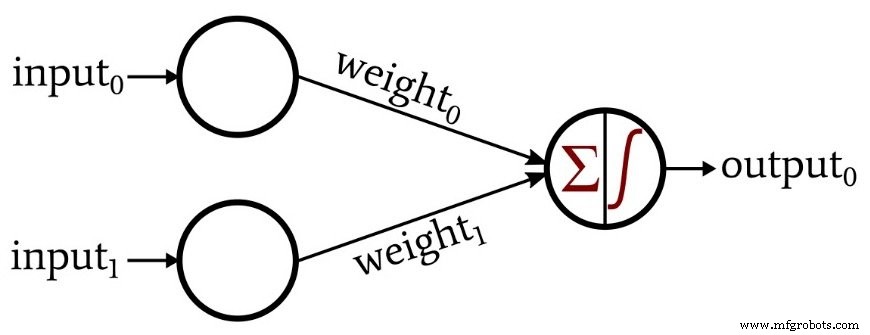
Observe que essa configuração é chamada de Perceptron de camada única. Sim, eu sei, tem duas camadas (entrada e saída), mas tem apenas uma camada que contém nós computacionais.

Classificando com um Perceptron

Neste artigo, vamos explorar a funcionalidade do Perceptron usando a seguinte rede neural.

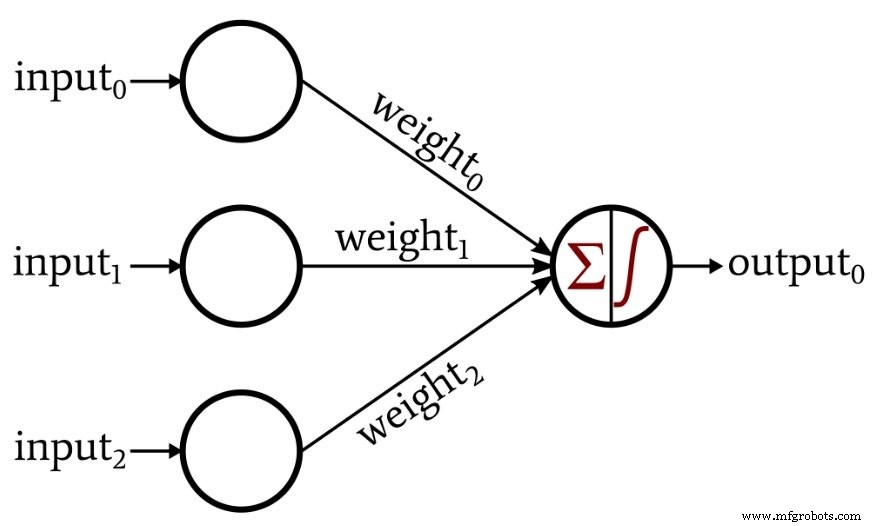
Como você pode ver, nossa dimensionalidade de entrada é três. Podemos pensar neste Perceptron como uma ferramenta para resolver problemas no espaço tridimensional. Por exemplo, vamos propor o seguinte problema:Se um ponto no espaço tridimensional está localizado abaixo do eixo x, ele corresponde a um datum inválido. Se o ponto estiver no eixo x ou acima dele, ele corresponde a um datum válido que deve ser retido para análise posterior. Precisamos dessa rede neutra para categorizar nossos dados, com um valor de saída 1 indicando um dado válido e um valor 0 indicando um dado inválido.

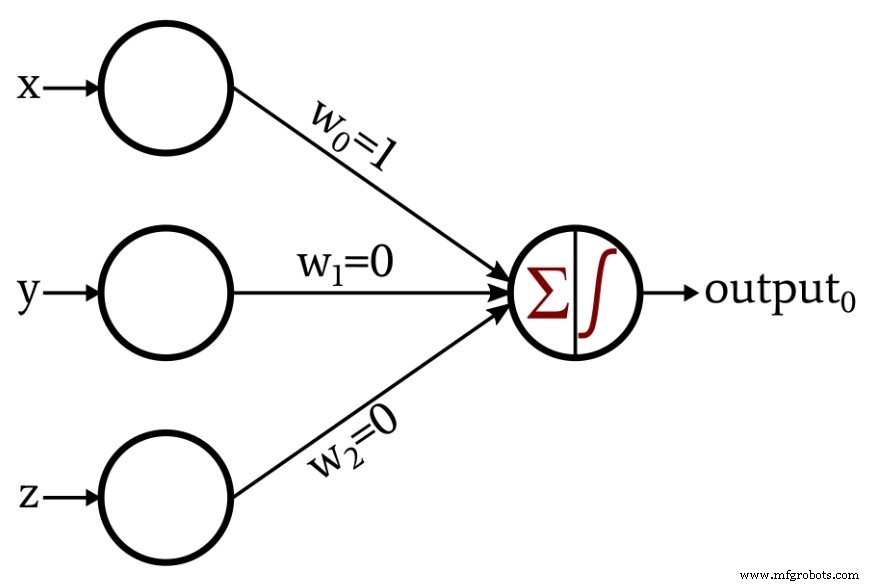
Primeiro, devemos mapear nossas coordenadas tridimensionais para o vetor de entrada. Neste exemplo, insira ₀ é o componente x, insira ₁ é o componente y, e entrada ₂ é o componente z. Em seguida, precisamos determinar os pesos. Este exemplo é tão simples que não precisamos treinar a rede. Podemos simplesmente pensar sobre os pesos necessários e atribuí-los:

Tudo o que precisamos fazer agora é especificar que a função de ativação do nó de saída é uma etapa unitária expressa da seguinte forma:

\ [f (x) =\ begin {cases} 0 &x <0 \\ 1 &x \ geq 0 \ end {cases} \]



O Perceptron funciona assim:Desde w ₁ =0 e w ₂ =0, os componentes y e z não contribuem para a soma gerada pelo nó de saída. O único dado de entrada que afeta a soma é o componente x, que é entregue ao nó de saída sem modificações porque w ₀ =1. Se o ponto no espaço tridimensional estiver abaixo do eixo x, a soma do nó de saída será negativa e a função de ativação converterá este valor negativo na saída ₀ =0. Se o ponto no espaço tridimensional estiver no eixo x ou acima dele, a soma será igual ou maior que zero, e a função de ativação converterá isso na saída ₀ =1.

Resolvendo problemas com um Perceptron

Na seção anterior, descrevi nosso Perceptron como uma ferramenta para resolver problemas. Você deve ter notado, porém, que o Perceptron não resolveu muitos problemas— eu resolveu o problema e deu a solução para o Perceptron atribuindo os pesos necessários.

Neste ponto, chegamos a um conceito crucial de rede neural:fui capaz de resolver rapidamente o problema de classificação válido / inválido porque a relação entre os dados de entrada e os valores de saída desejados é muito simples. No entanto, em muitas situações da vida real, seria extremamente difícil para um ser humano formular uma relação matemática entre os dados de entrada e os valores de saída. Podemos adquirir dados de entrada e podemos registrar ou produzir valores de saída correspondentes, mas não temos uma rota matemática da entrada para a saída.

Um exemplo útil é o reconhecimento de manuscrito. Digamos que temos imagens de caracteres escritos à mão e queremos categorizar essas imagens como "a", "b", "c" etc., para que possamos converter a escrita à mão em texto normal de computador. Qualquer pessoa que saiba escrever e ler será capaz de gerar imagens de entrada e, em seguida, atribuir categorias corretas a cada imagem. Assim, coletar dados de entrada e dados de saída correspondentes não é difícil. Por outro lado, seria extremamente difícil olhar para os pares de entrada-saída e formular uma expressão matemática ou algoritmo que convertesse corretamente as imagens de entrada em uma categoria de saída.

Assim, o reconhecimento de caligrafia e muitas outras tarefas de processamento de sinais apresentam problemas matemáticos que os seres humanos não podem resolver sem a ajuda de ferramentas sofisticadas. Apesar do fato de que as redes neurais não podem pensar, analisar e inovar, elas nos permitem resolver esses problemas difíceis porque podem fazer algo que os seres humanos não podem, ou seja, realizar cálculos rápida e repetidamente envolvendo quantidades potencialmente imensas de dados numéricos .



Treinamento da rede

O processo que permite a uma rede neural criar um caminho matemático da entrada à saída é chamado de treinamento. Fornecemos os dados de treinamento da rede que consistem em valores de entrada e valores de saída correspondentes, e ela aplica um procedimento matemático fixo a esses valores. O objetivo deste procedimento é modificar gradualmente os pesos da rede de modo que a rede seja capaz de calcular os valores de saída corretos, mesmo com dados de entrada que nunca viu antes. É essencialmente encontrar padrões nos dados de treinamento e gerar pesos que produzirão resultados úteis ao aplicar esses padrões a novos dados.

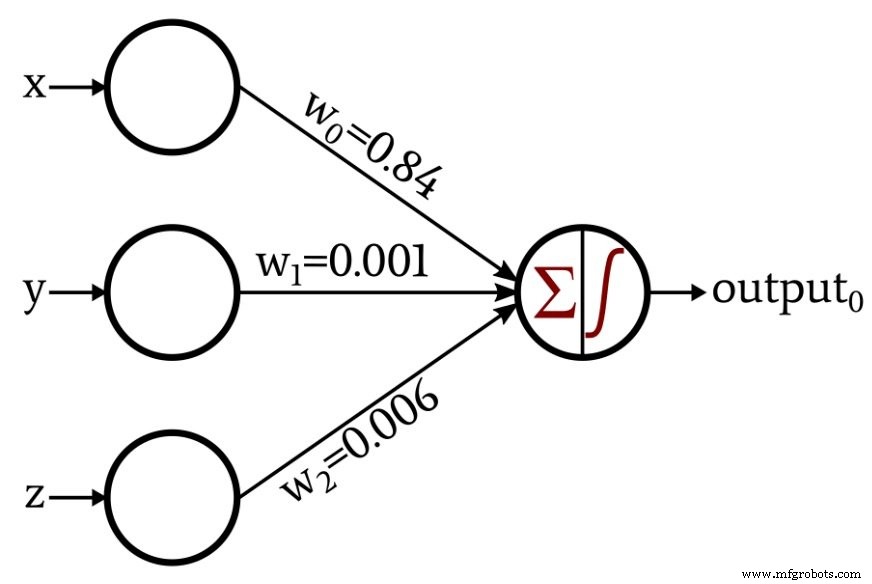
O diagrama a seguir mostra o classificador válido / inválido discutido acima, mas os pesos são diferentes. Esses são pesos que eu gerei treinando o Perceptron com 1000 pontos de dados. Como você pode ver, o processo de treinamento permitiu ao Perceptron aproximar-se automaticamente da relação matemática que identifiquei por meio do pensamento crítico de estilo humano.

No próximo artigo…

Eu mostrei a vocês os resultados do treinamento deste Perceptron, mas não disse nada sobre como obtive esses resultados. O próximo artigo descreverá um programa curto em Python que implementa uma rede neural Perceptron de camada única e também explicarei meu procedimento de treinamento.