Decibéis

O Bel é usado para representar ganho

Em sua forma mais simples, o ganho de um amplificador é uma proporção de saída sobre entrada. Como todas as proporções, essa forma de ganho não tem unidade. No entanto, existe uma unidade real destinada a representar o ganho, e é chamada de bel .

Como uma unidade, o bel foi concebido como uma maneira conveniente de representar a perda de poder na fiação do sistema telefônico, em vez de ganho em amplificadores. O nome da unidade é derivado de Alexander Graham Bell, o famoso inventor escocês cujo trabalho foi fundamental no desenvolvimento de sistemas telefônicos. Originalmente, o bel representava a quantidade de perda de potência do sinal devido à resistência em um comprimento padrão de cabo elétrico. Agora, é definido em termos do logaritmo comum (base 10) de uma relação de potência (potência de saída dividida pela potência de entrada):

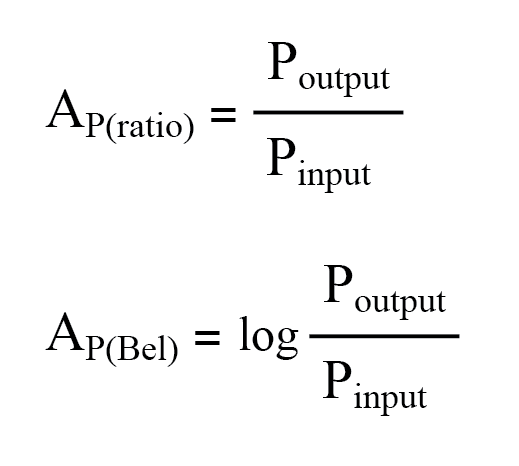
O Bel é não linear

Como o bel é uma unidade logarítmica, não é linear. Para dar uma ideia de como isso funciona, considere a seguinte tabela de figuras, comparando perdas e ganhos de potência em bels versus proporções simples:

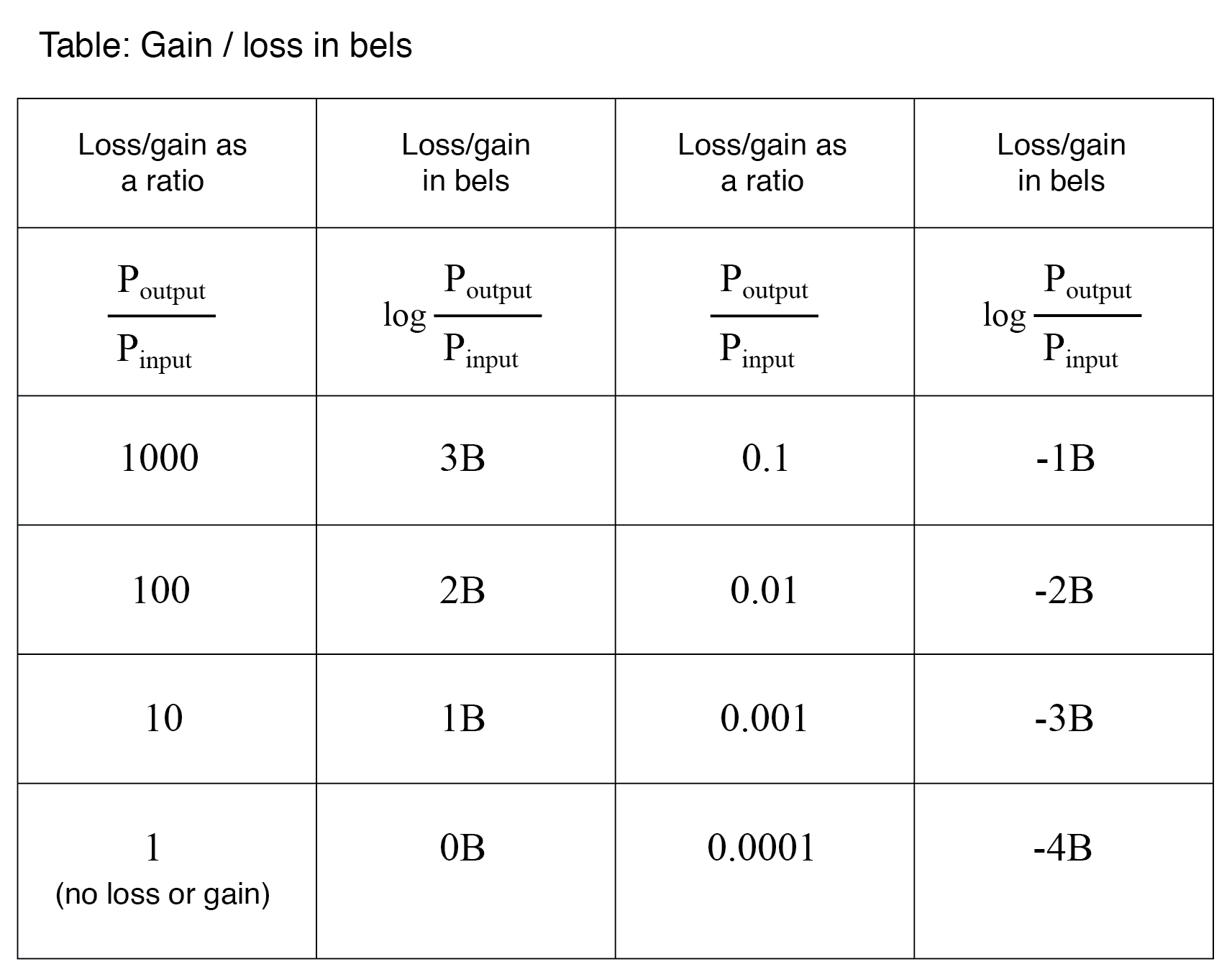
Movendo do Bel para o Decibel

Posteriormente, foi decidido que o bel era uma unidade muito grande para ser usado diretamente e, portanto, tornou-se comum aplicar o prefixo métrico deci (significando 1/10) para ele, tornando-o deci bels ou dB. Agora, a expressão “dB” é tão comum que muitas pessoas não percebem que é uma combinação de “deci-” e “-bel”, ou que existe mesmo uma unidade como o “bel”. Para colocar isso em perspectiva, aqui está outra tabela contrastando as taxas de ganho / perda de potência em relação aos decibéis:



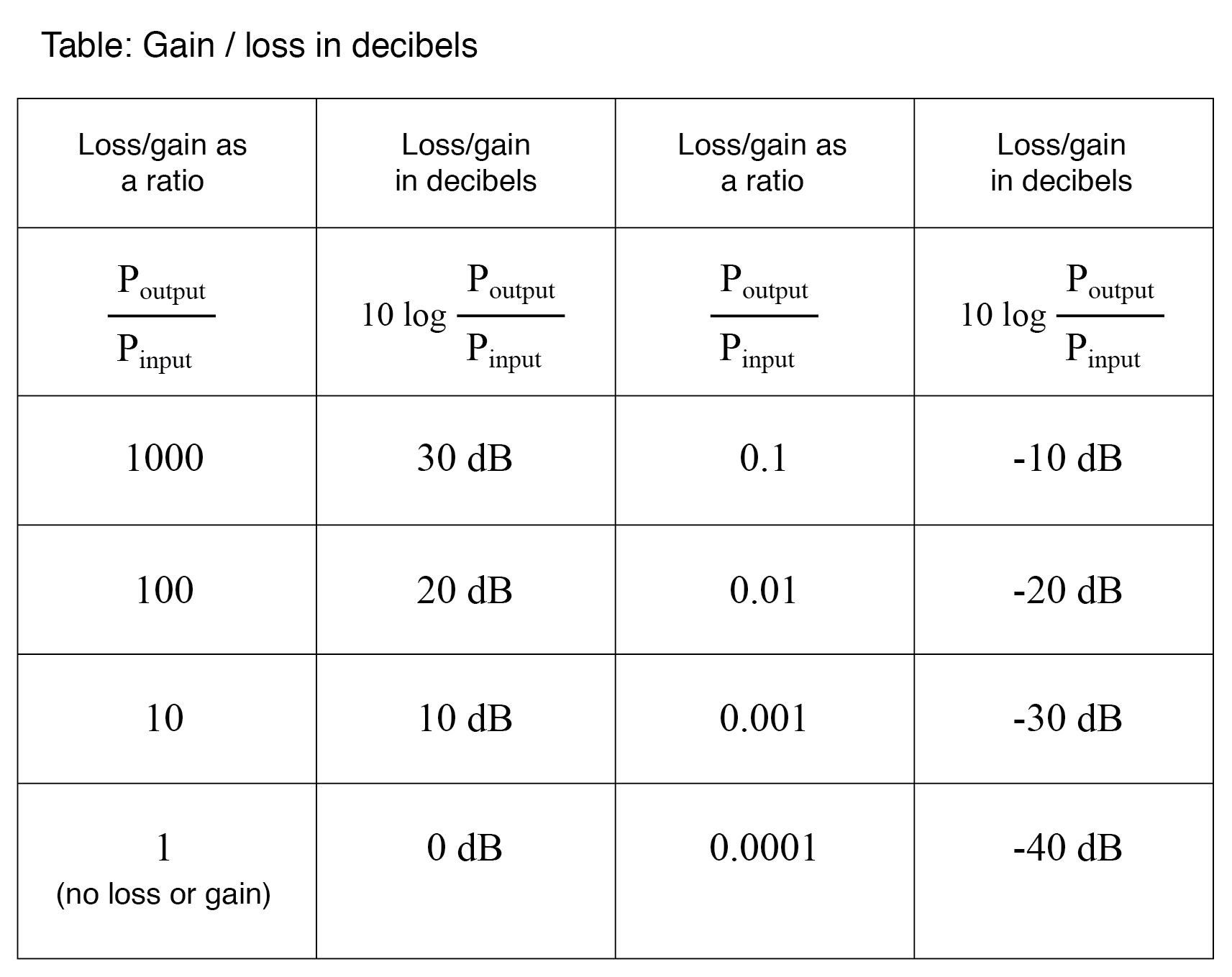
Como uma unidade logarítmica, este modo de expressão de ganho de potência cobre uma ampla gama de proporções com um intervalo mínimo em números. É razoável perguntar:“por que alguém sentiu a necessidade de inventar um logarítmico unidade para perda de energia do sinal elétrico em um sistema telefônico? ” A resposta está relacionada à dinâmica da audição humana, cuja intensidade perceptiva é logarítmica por natureza.

A audição humana é não linear

A audição humana é altamente não linear:para dobrar a intensidade percebida de um som, a potência sonora real deve ser multiplicada por um fator de dez. Relacionar a perda de potência do sinal do telefone em termos da escala logarítmica “bel” faz todo o sentido neste contexto:uma perda de potência de 1 bel se traduz em uma perda de som percebida de 50 por cento, ou 1/2. Um ganho de potência de 1 bel traduz-se na duplicação da intensidade percebida do som.

Outros exemplos de escala logarítmica:escala de Richter e pH químico

Escala Richter

Uma analogia quase perfeita com a escala bel é a escala Richter usada para descrever a intensidade do terremoto:um terremoto Richter 6.0 é 10 vezes mais poderoso do que um terremoto Richter 5.0; um terremoto 7.0 Richter 100 vezes mais poderoso do que um terremoto 5.0 Richter; um terremoto 4.0 Richter é 1/10 tão poderoso quanto um terremoto 5.0 Richter e assim por diante.

pH químico

A escala de medição do pH químico é igualmente logarítmica, uma diferença de 1 na escala é equivalente a uma diferença de dez vezes na concentração de íons de hidrogênio de uma solução química. Uma vantagem de usar uma escala de medição logarítmica é a enorme gama de expressão proporcionada por um intervalo relativamente pequeno de valores numéricos, e é essa vantagem que garante o uso de números de Richter para terremotos e pH para atividade de íons de hidrogênio.

Usando o Bel para expressar ganhos e perdas do sistema

Outra razão para a adoção do bel como unidade de ganho é a simples expressão dos ganhos e perdas do sistema. Considere o último exemplo de sistema (figura acima), onde dois amplificadores foram conectados em conjunto para amplificar um sinal. O respectivo ganho para cada amplificador foi expresso como uma razão, e o ganho geral para o sistema foi o produto (multiplicação) dessas duas razões:

 Ganho geral =(3) (5) =15 

Se essas figuras representassem poder ganhos, poderíamos aplicar diretamente a unidade de bels à tarefa de representar o ganho de cada amplificador e do sistema como um todo. (Figura abaixo)



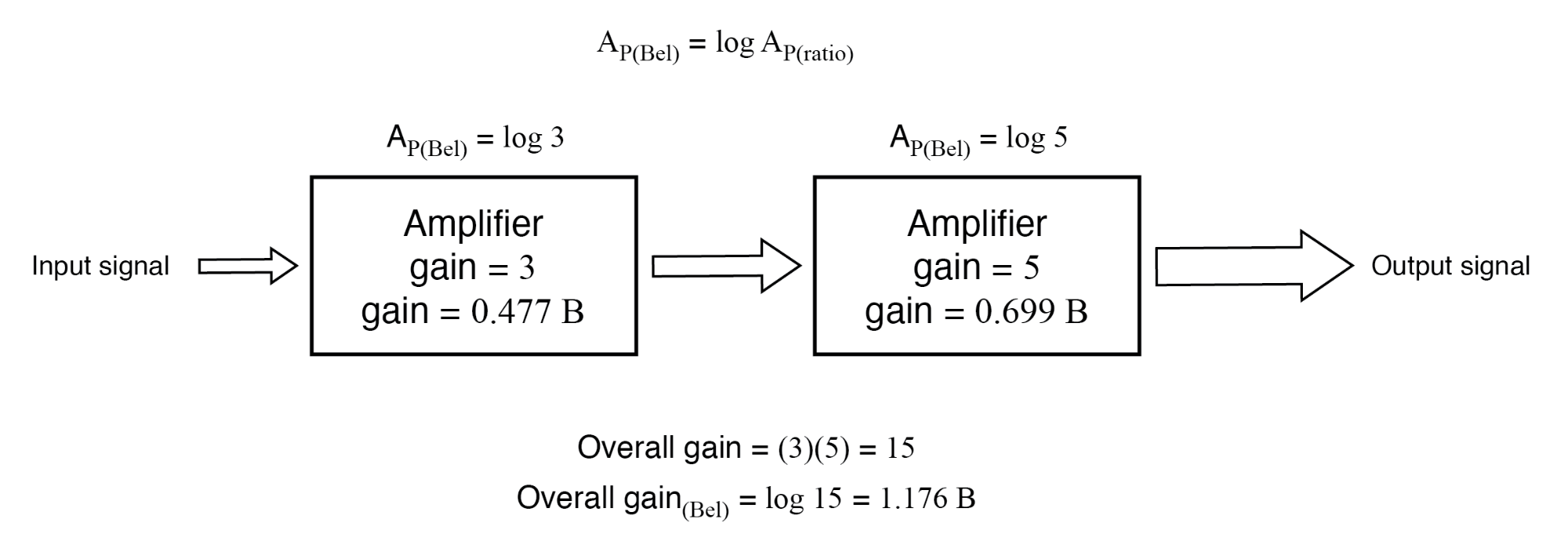
O ganho de potência em bels é aditivo:0,477 B + 0,699 B =1,176 B.

Uma inspeção cuidadosa desses números de ganho na unidade de "bel" produz uma descoberta:eles são aditivos. Os valores de ganho de proporção são multiplicativos para amplificadores encenados, mas os ganhos são expressos em bels add em vez de multiplicar para igualar o ganho geral do sistema. O primeiro amplificador com seu ganho de potência de 0,477 B adiciona ao ganho de potência do segundo amplificador de 0,699 B para fazer um sistema com um ganho de potência geral de 1,176 B.

Ganhos usando decibéis

Recalculando decibéis em vez de bels, notamos o mesmo fenômeno. (Figura abaixo)



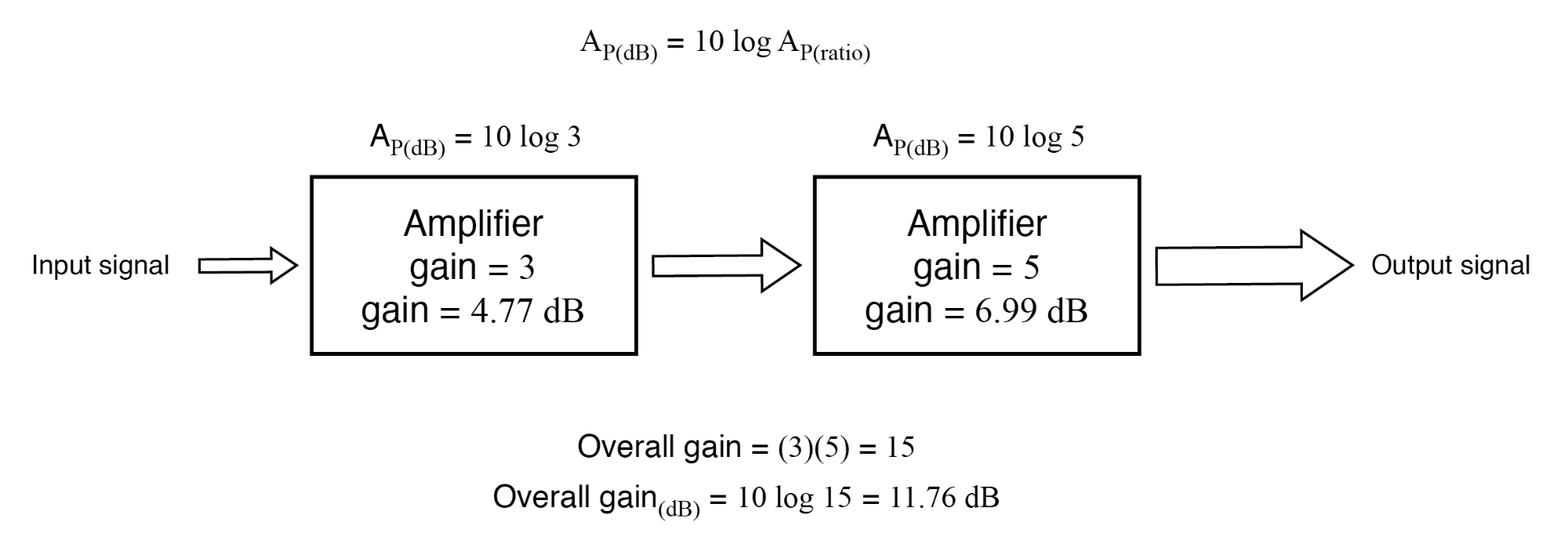
O ganho dos estágios do amplificador em decibéis é aditivo:4,77 dB + 6,99 dB =11,76 dB.

Para aqueles que já estão familiarizados com as propriedades aritméticas dos logaritmos, isso não é surpresa. É uma regra elementar da álgebra que o antilogaritmo da soma dos valores do logaritmo de dois números seja igual ao produto dos dois números originais. Em outras palavras, se pegarmos dois números e determinarmos o logaritmo de cada um, adicionarmos esses dois logaritmos juntos e determinarmos o "antilogaritmo" dessa soma (elevar o número base do logaritmo - neste caso, 10 - para o potência dessa soma), o resultado será o mesmo como se tivéssemos simplesmente multiplicado os dois números originais.

Esta regra algébrica forma o coração de um dispositivo chamado régua de cálculo , um computador analógico que poderia, entre outras coisas, determinar os produtos e quocientes de números por adição (somando comprimentos físicos marcados em escalas deslizantes de madeira, metal ou plástico).

Dada uma tabela de figuras logarítmicas, o mesmo truque matemático poderia ser usado para realizar multiplicações e divisões complexas, bastando fazer adições e subtrações, respectivamente. Com o advento de calculadoras digitais portáteis de alta velocidade, essa elegante técnica de cálculo praticamente desapareceu do uso popular. No entanto, ainda é importante entender quando se trabalha com escalas de medição que são logarítmicas por natureza, como as escalas bel (decibéis) e Richter.

Conversão de decibéis e proporção sem unidade

Ao converter um ganho de potência de unidades de bels ou decibéis em uma razão sem unidade, a função matemática inversa de logaritmos comuns é usada:potências de 10, ou o antilog .



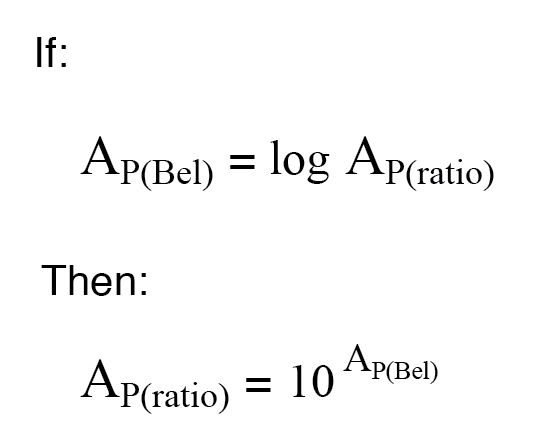
Converter decibéis em proporções sem unidade para ganho de potência é praticamente o mesmo, apenas um fator de divisão de 10 é incluído no termo expoente:



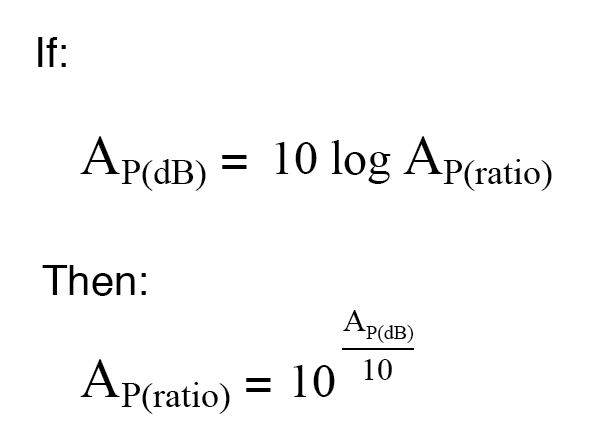
Exemplo: A potência de um amplificador é de 1 Watt, a saída de potência é de 10 Watts. Encontre o ganho de potência em dB.

 AP (dB) =10 * log10 (PO / PI) =10 * log10 (10/1) =10 * log10 (10) =10 * (1) =10 dB 

Exemplo: Encontre a relação de ganho de potência AP (relação) =(PO / PI) para um ganho de potência de 20 dB.

 AP (dB) =20 =10 * log10 (razão de  AP  ) 20/10 =log10 * (AP  proporção  ) 10 ^ (20/10) =10 ^ (log10 * (AP  proporção  )) 10 ^ 2 =100 =AP (proporção) =(PO / PI) 

Conversão do ganho de potência em ganho de tensão / corrente

Porque o bel é fundamentalmente uma unidade de poder ganho ou perda em um sistema, os ganhos e perdas de tensão ou corrente não se convertem em bels ou dB exatamente da mesma maneira. Ao usar bels ou decibéis para expressar um ganho diferente de potência, seja tensão ou corrente, devemos realizar o cálculo em termos de quanto ganho de potência haveria para aquela quantidade de tensão ou ganho de corrente.

Para uma impedância de carga constante, um ganho de tensão ou corrente de 2 equivale a um ganho de potência de 4 (2 ² ); uma tensão ou ganho de corrente de 3 equivale a um ganho de potência de 9 (3 ² ) Se multiplicarmos a tensão ou a corrente por um determinado fator, o ganho de potência incorrido por essa multiplicação será o quadrado desse fator. Isso se relaciona com as formas da Lei de Joule, onde a potência foi calculada a partir da tensão ou da corrente e da resistência:



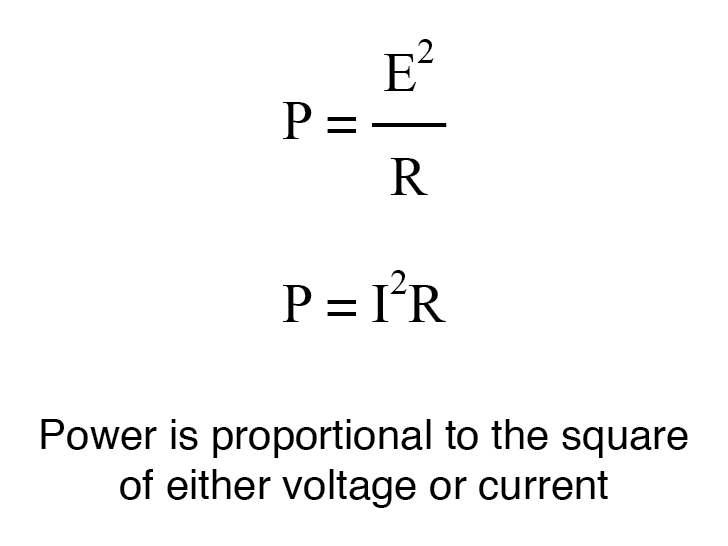
Assim, ao traduzir um ganho de tensão ou corrente razão em um ganho respectivo em termos da unidade bel, devemos incluir este expoente na (s) equação (ões):



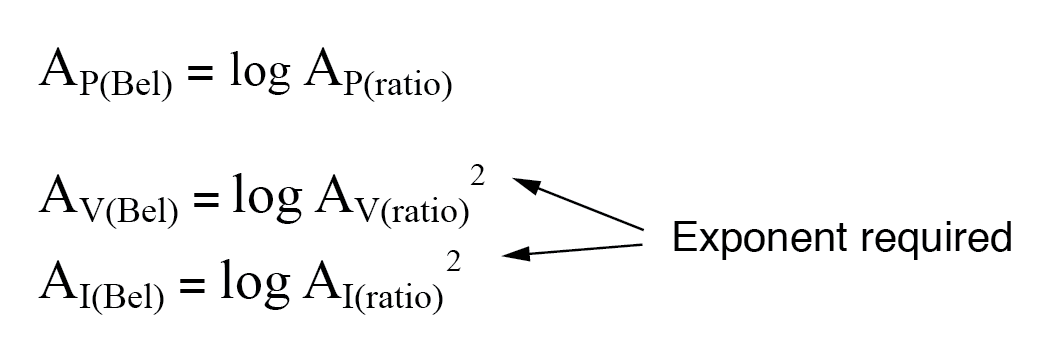
O mesmo requisito de expoente é verdadeiro ao expressar ganhos de tensão ou corrente em termos de decibéis:



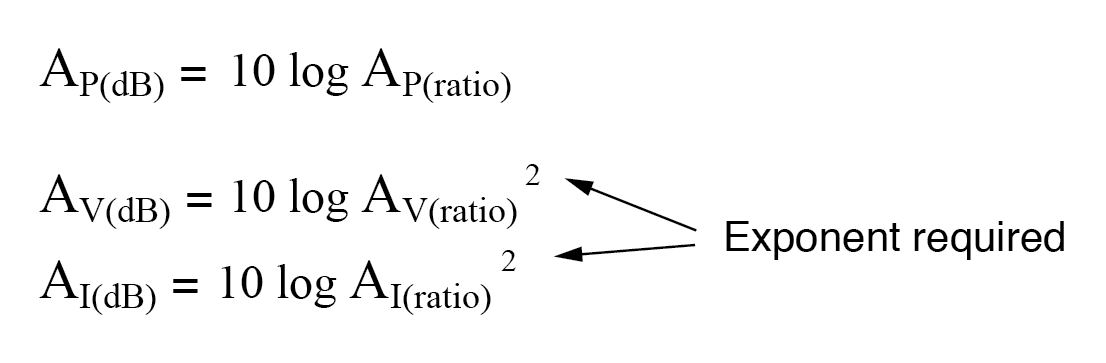
No entanto, graças a outra propriedade interessante dos logaritmos, podemos simplificar essas equações para eliminar o expoente incluindo o “2” como um fator de multiplicação para a função logaritmo. Em outras palavras, em vez de tomar o logaritmo do quadrado da tensão ou ganho de corrente, nós apenas multiplicamos a figura do logaritmo de ganho de tensão ou corrente por 2 e o resultado final em bels ou decibéis será o mesmo:



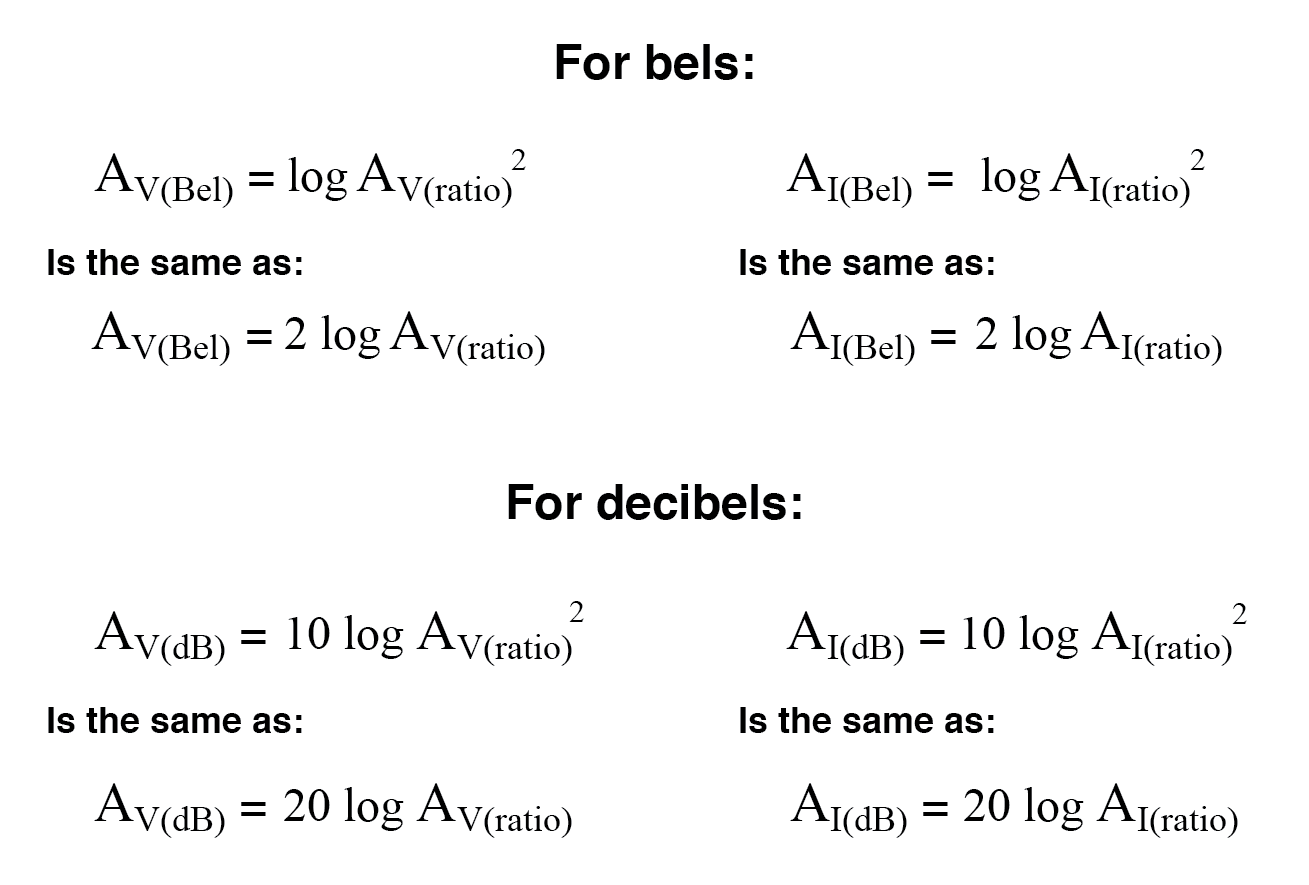
O processo de conversão de tensão ou ganhos de corrente de bels ou decibéis em proporções sem unidade é quase o mesmo que para ganhos de potência:



Aqui estão as equações usadas para converter os ganhos de tensão ou corrente em decibéis em razões sem unidade:



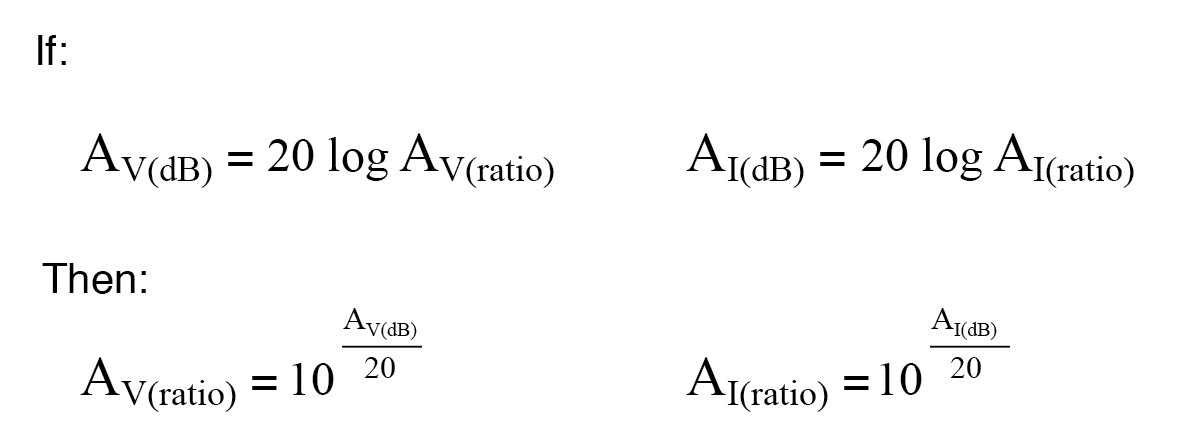
Embora o bel seja uma unidade naturalmente dimensionada para potência, outra unidade logarítmica foi inventada para expressar diretamente a tensão ou os ganhos / perdas de corrente, e é baseada no natural logaritmo em vez do comum logaritmo como bels e decibéis são. Chamado de neper , seu símbolo de unidade é “Np; entretanto, “n” minúsculo pode ser encontrado.



Para o bem ou para o mal, nem o neper nem seu primo atenuado, o decineper , é popularmente usado como uma unidade em aplicações de engenharia americanas. Exemplo: A tensão em um amplificador de linha de áudio de 600 Ω é 10 mV, a tensão em uma carga de 600 Ω é 1 V. Encontre o ganho de potência em dB.

 A (dB) =20 log10 (VO / VI) =20 log10 (1 / 0,01) =20 log10 (100) =20 (2) =40 dB 

Exemplo: Encontre a razão de ganho de tensão AV (razão) =(VO / VI) para um amplificador de ganho de 20 dB com uma impedância de entrada e saída de 50 Ω.

 AV (dB) =20 log10 AV (proporção) 20 =20 log10 AV (proporção) 20/20 =log10 AP (proporção) 1020/20 =10log10 (AV (proporção)) 10 =AV (proporção) =( VO / VI) 

Uma revisão do decibel

• Ganhos e perdas podem ser expressos em termos de uma proporção sem unidade, ou na unidade de bels (B) ou decibéis (dB). Um decibel é literalmente um deci -bel:um décimo de um bel.
• O bel é fundamentalmente uma unidade para expressar poder ganho ou perda. Para converter uma relação de potência em bels ou decibéis, use uma destas equações:

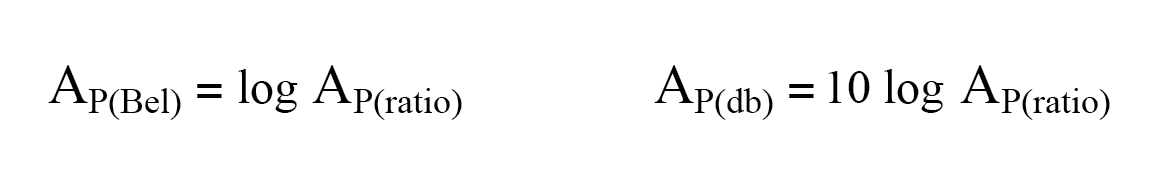
• Ao usar a unidade de bel ou decibel para expressar uma voltagem ou atual proporção, deve ser lançado em termos de um poder equivalente Razão. Praticamente, isso significa o uso de diferentes equações, com um fator de multiplicação de 2 para o valor do logaritmo correspondente a um expoente de 2 para a relação de ganho de tensão ou corrente:

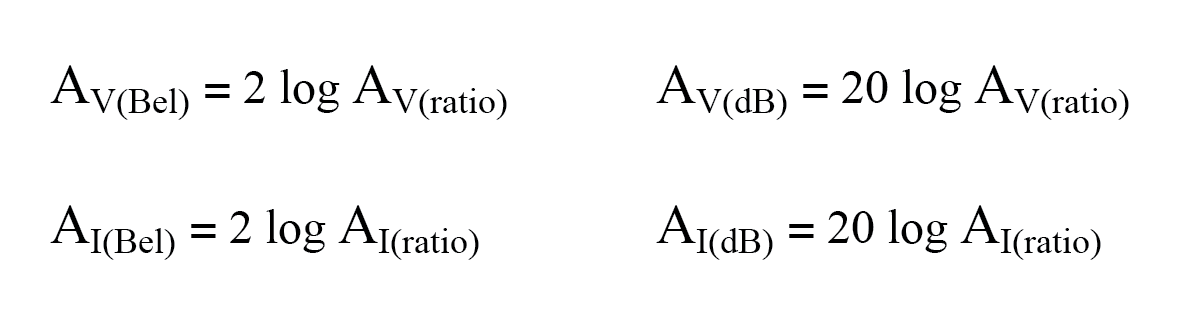
• Para converter um ganho de decibéis em um ganho de proporção sem unidade, use uma destas equações:

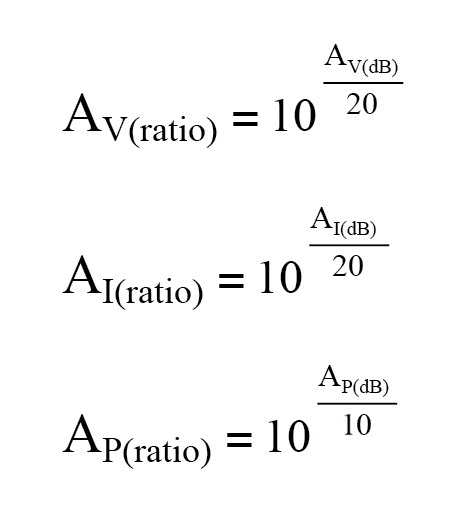
• Um ganho (amplificação) é expresso como um valor bel ou decibel positivo. Uma perda (atenuação) é expressa como um número bel ou decibel negativo. O ganho de unidade (sem ganho ou perda; razão =1) é expresso como zero bels ou zero decibéis.
• Ao calcular o ganho geral para um sistema de amplificador composto de vários estágios de amplificador, as taxas de ganho individuais são multiplicadas para encontrar a taxa de ganho geral. Os valores de bel ou decibéis para cada estágio do amplificador, por outro lado, são adicionados juntos para determinar o ganho geral.

PLANILHAS RELACIONADAS:

• Planilha de medições de decibéis
• Planilha de teoria do amplificador elementar