Medição de frequência e fase

Uma quantidade elétrica importante sem equivalente em circuitos DC é frequência .

A medição de frequência é muito importante em muitas aplicações de corrente alternada, especialmente em sistemas de energia CA projetados para funcionar com eficiência em uma frequência e apenas uma frequência.

Se a CA está sendo gerada por um alternador eletromecânico, a frequência será diretamente proporcional à velocidade do eixo da máquina, e a frequência pode ser medida simplesmente medindo a velocidade do eixo.

Se a frequência precisar ser medida a alguma distância do alternador, entretanto, outros meios de medição serão necessários.

Método de medição de frequência

Usando o Princípio da Ressonância Mecânica

Um método simples, mas bruto, de medição de frequência em sistemas de potência utiliza o princípio da ressonância mecânica. Todo objeto físico que possui a propriedade de elasticidade (elasticidade) tem uma frequência inerente na qual prefere vibrar.

O diapasão é um grande exemplo disso:toque nele uma vez e ele continuará a vibrar em um tom específico para o seu comprimento. Os diapasões mais longos têm frequências ressonantes mais baixas:seus tons serão mais baixos na escala musical do que os garfos mais curtos.

Imagine uma fileira de diapasões de tamanho progressivo, dispostos lado a lado. Eles são todos montados em uma base comum, e essa base é vibrada na frequência da tensão CA (ou corrente) medida por meio de um eletroímã.

O diapasão que estiver mais próximo em frequência de ressonância da frequência dessa vibração tenderá a tremer mais (ou mais alto). Se os dentes dos garfos fossem frágeis o suficiente, poderíamos ver o movimento relativo de cada um pelo comprimento do desfoque que veríamos ao inspecionar cada um de uma perspectiva de vista final.

Bem, faça uma coleção de “diapasões” de uma tira de chapa cortada em um padrão semelhante a um ancinho e você terá a palheta vibrante medidor de frequência:

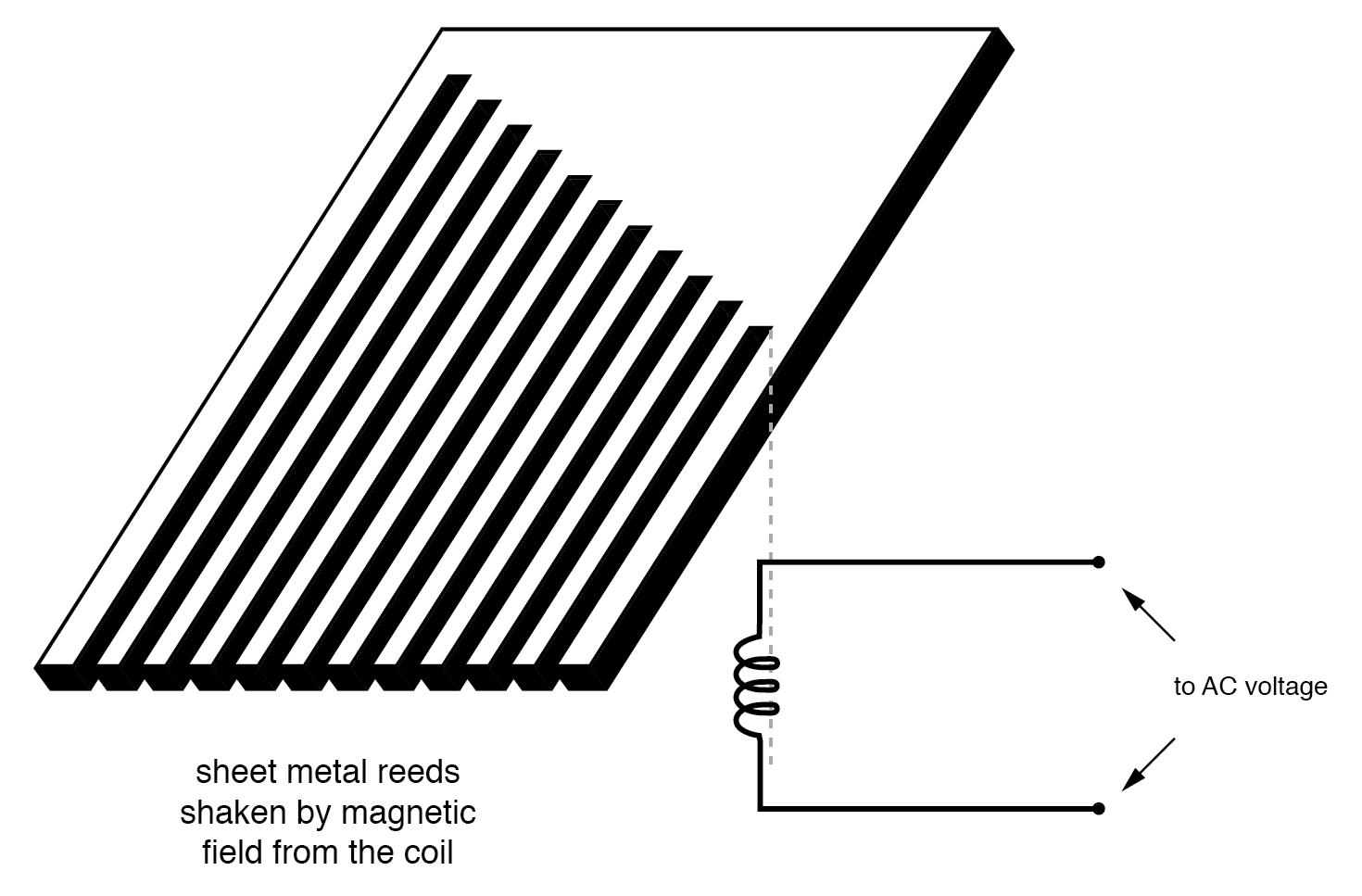
Diagrama do medidor de frequência de palheta vibratória.



O usuário deste medidor vê as extremidades de todas aquelas palhetas de comprimento desigual à medida que são sacudidas coletivamente na frequência da tensão CA aplicada à bobina. O mais próximo em frequência ressonante da CA aplicada vibrará mais, parecendo algo como:

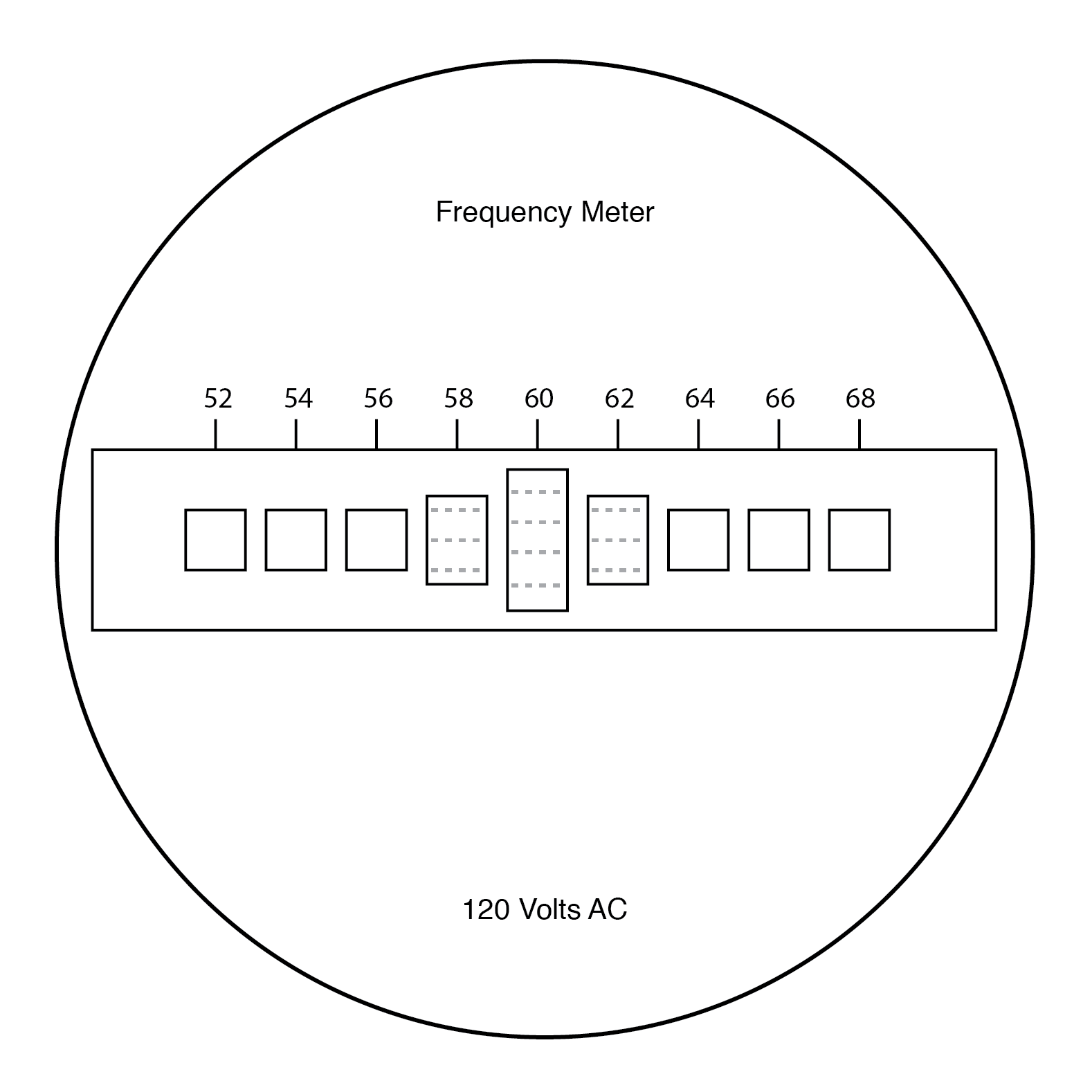
Painel frontal do medidor de frequência de palheta vibratória.



Os medidores vibratórios de palheta, obviamente, não são instrumentos de precisão, mas são muito simples e, portanto, fáceis de fabricar para serem robustos. Eles são freqüentemente encontrados em pequenos grupos geradores movidos a motor com o propósito de definir a velocidade do motor de forma que a frequência seja um pouco próxima a 60 (50 na Europa) Hertz.

Usando uma forma de circuito de tanque

Embora os medidores do tipo palheta sejam imprecisos, seu princípio operacional não é. No lugar da ressonância mecânica, podemos substituir a ressonância elétrica e projetar um medidor de frequência usando um indutor e um capacitor na forma de um circuito tanque (indutor paralelo e capacitor). Veja a figura abaixo.

Um ou ambos os componentes são ajustados e um medidor é colocado no circuito para indicar a amplitude máxima da tensão entre os dois componentes.

O (s) botão (ões) de ajuste são calibrados para mostrar a frequência de ressonância para qualquer configuração dada, e a frequência é lida a partir deles depois que o dispositivo foi ajustado para a indicação máxima no medidor.

Essencialmente, este é um circuito de filtro sintonizável que é ajustado e então lido de maneira semelhante a um circuito de ponte (que deve ser balanceado para uma condição “nula” e então lido).

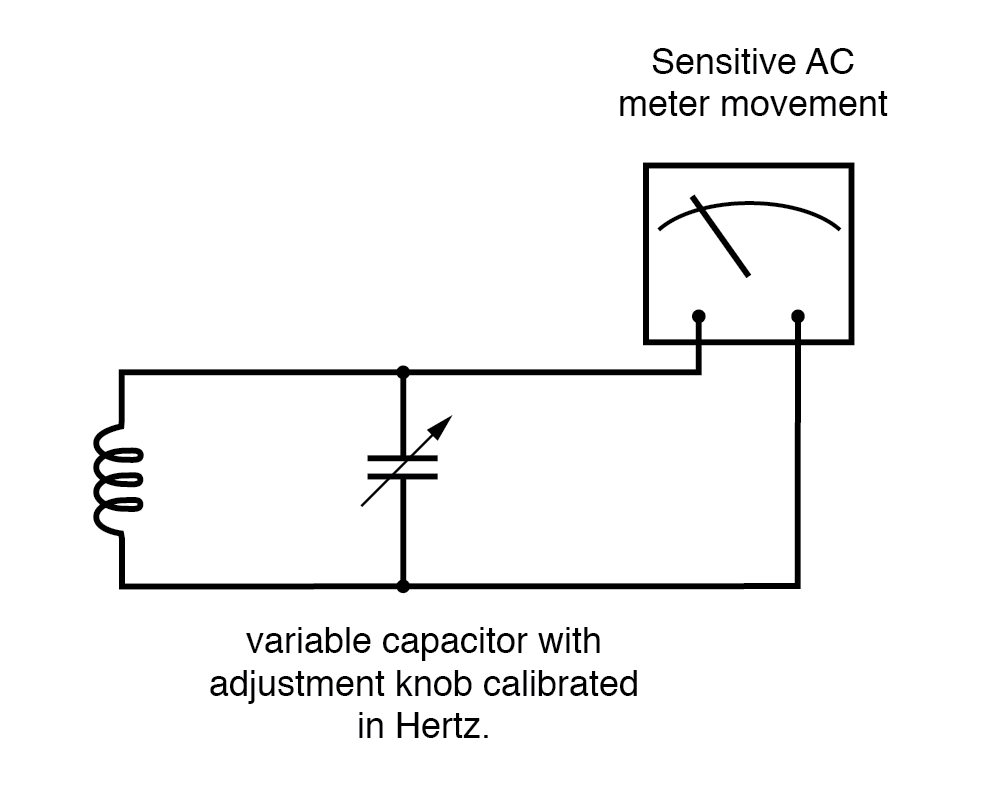
O medidor de frequência ressonante atinge o pico quando a frequência ressonante L-C é sintonizada para testar a frequência.



Esta técnica é popular para operadores de rádio amadores (ou pelo menos era antes do advento de instrumentos de frequência digital baratos chamados contadores ), especialmente porque não requer conexão direta com o circuito.

Contanto que o indutor e / ou capacitor possam interceptar campo disperso suficiente (magnético ou elétrico, respectivamente) do circuito em teste para fazer com que o medidor indique, ele funcionará.

Na frequência, como em outros tipos de medição elétrica, os meios de medição mais precisos são geralmente aqueles em que uma quantidade desconhecida é comparada com um padrão conhecido , o instrumento básico nada mais faz do que indicar quando as duas quantidades são iguais uma à outra.

Este é o princípio básico por trás do circuito de ponte DC (Wheatstone) e é um princípio metrológico sólido aplicado em todas as ciências. Se tivermos acesso a um padrão de frequência preciso (uma fonte de voltagem CA mantida com muita precisão em uma única frequência), a medição de uma frequência desconhecida, por comparação, deve ser relativamente fácil.

Usando Cristal de Quartzo

Para esse padrão de frequência, voltamos nossa atenção para o diapasão, ou pelo menos uma variação mais moderna dele chamada de cristal de quartzo .

O quartzo é um mineral natural que possui uma propriedade muito interessante chamada piezoeletricidade . Os materiais piezoelétricos produzem uma tensão em todo o seu comprimento quando fisicamente estressados ​​e se deformam fisicamente quando uma tensão externa é aplicada em seus comprimentos.

Essa deformação é muito, muito leve na maioria dos casos, mas existe.

A rocha de quartzo é elástica (elástica) dentro daquela pequena faixa de curvatura que uma voltagem externa produziria, o que significa que ela terá uma frequência ressonante mecânica própria, capaz de se manifestar como um sinal de voltagem elétrica.

Em outras palavras, se um chip de quartzo for atingido, ele "tocará" com sua própria frequência única determinada pelo comprimento do chip, e essa oscilação ressonante produzirá uma voltagem equivalente em vários pontos do chip de quartzo que podem ser tocados em por fios fixados à superfície do chip.

De maneira recíproca, o chip de quartzo tende a vibrar mais quando é “excitado” por uma tensão CA aplicada na freqüência correta, exatamente como as palhetas em um medidor de freqüência de palheta vibratória.

Pedaços de rocha de quartzo podem ser cortados com precisão para as frequências ressonantes desejadas, e esse chip montado com segurança dentro de uma casca protetora com fios estendidos para conexão a um circuito elétrico externo.

Quando embalado como tal, o dispositivo resultante é simplesmente chamado de cristal (ou às vezes “ xtal ”). O símbolo esquemático é mostrado na figura abaixo.

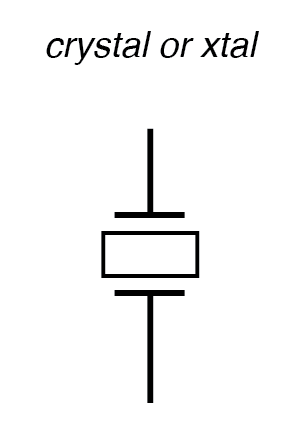
Símbolo esquemático de cristal (elemento determinante de frequência).



Eletricamente, esse chip de quartzo é equivalente a um circuito ressonante LC em série. (Figura abaixo) As propriedades dielétricas do quartzo contribuem com um elemento capacitivo adicional para o circuito equivalente.

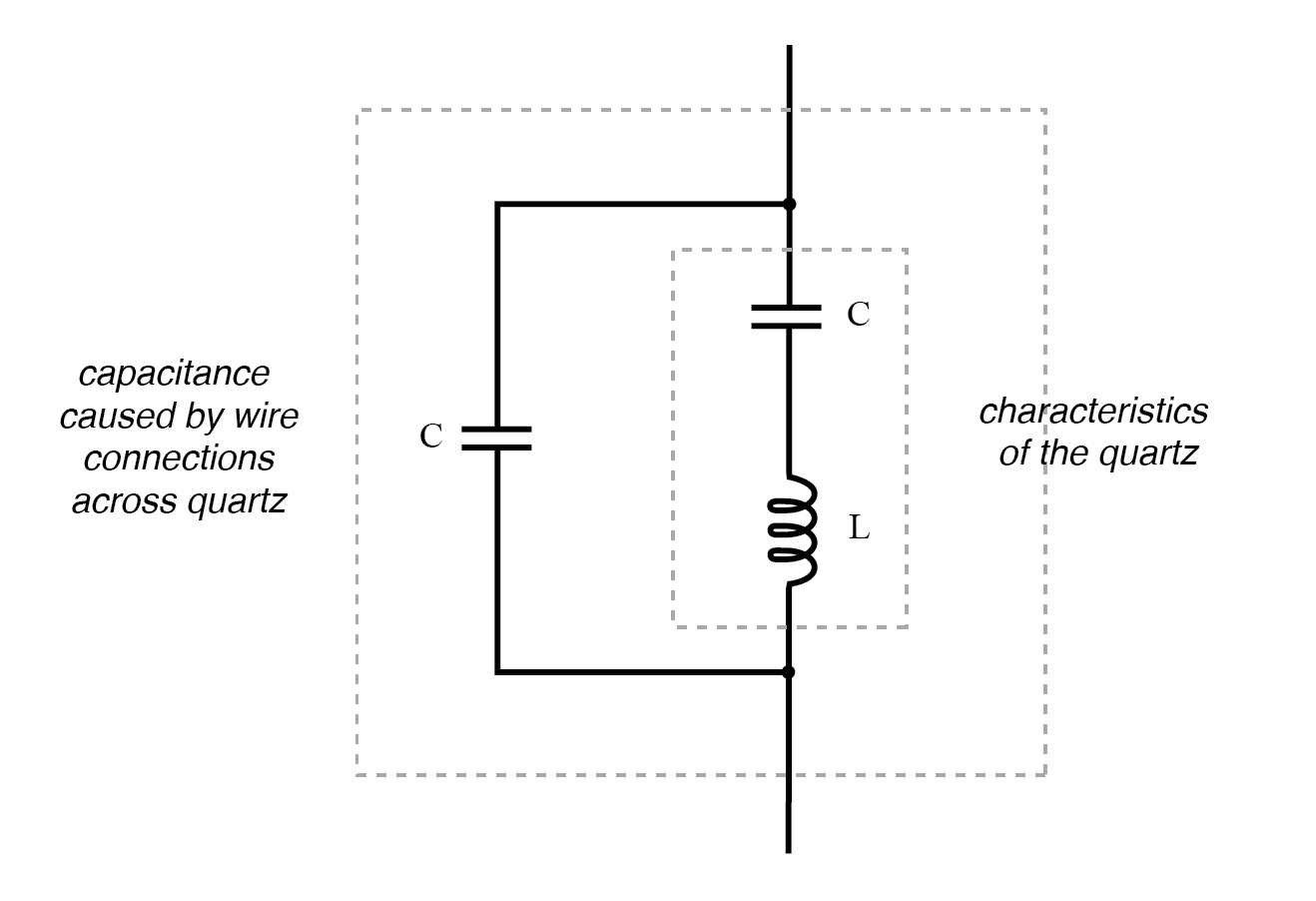
Circuito equivalente de cristal de quartzo.



A "capacitância" e a "indutância" mostradas em série são meramente equivalentes elétricos das propriedades de ressonância mecânica do quartzo:elas não existem como componentes discretos dentro do cristal. A capacitância mostrada em paralelo devido às conexões dos fios através do corpo dielétrico (isolante) de quartzo é real e tem um efeito na resposta ressonante de todo o sistema.

Uma discussão completa sobre a dinâmica do cristal não é necessária aqui, mas o que precisa ser entendido sobre os cristais é a equivalência do circuito ressonante e como ela pode ser explorada dentro de um circuito oscilador para obter uma tensão de saída com uma frequência conhecida e estável.

Cristais, como elementos ressonantes, normalmente têm um "Q" muito maior ( qualidade ) valores do que os circuitos tanque construídos a partir de indutores e capacitores, principalmente devido à relativa ausência de resistência parasita, tornando suas frequências de ressonância muito definidas e precisas.

Como a frequência ressonante depende unicamente das propriedades físicas do quartzo (uma substância muito estável, mecanicamente), a variação da frequência ressonante ao longo do tempo com um cristal de quartzo é muito, muito baixa. É assim que o movimento de quartzo os relógios obtêm sua alta precisão:por meio de um oscilador eletrônico estabilizado pela ação ressonante de um cristal de quartzo.

Para aplicações de laboratório, entretanto, uma estabilidade de frequência ainda maior pode ser desejada. Para isso, o cristal em questão pode ser colocado em um ambiente com temperatura estabilizada (geralmente um forno), eliminando erros de frequência devido à expansão e contração térmica do quartzo.

Para o máximo em um padrão de frequência, porém, nada descoberto até agora supera a precisão de um único átomo ressonante. Este é o princípio do chamado relógio atômico , que usa um átomo de mercúrio (ou césio) suspenso no vácuo, excitado por energia externa para ressoar em sua própria frequência única.

A frequência resultante é detectada como um sinal de ondas de rádio e forma a base para os relógios mais precisos conhecidos pela humanidade. Laboratórios de padrões nacionais em todo o mundo mantêm alguns desses relógios hiperprecisos e transmitem sinais de frequência com base nas vibrações desses átomos para cientistas e técnicos sintonizarem e usarem para fins de calibração de frequência.

Parte Prática

Agora chegamos à parte prática:assim que tivermos uma fonte de frequência precisa, como podemos comparar isso com uma frequência desconhecida para obter uma medição?

Uma maneira é usar um CRT como dispositivo de comparação de frequência. Os tubos de raios catódicos normalmente têm meios de desviar o feixe de elétrons nos eixos horizontal e vertical.

Se as placas de metal forem usadas para desviar eletrostaticamente os elétrons, haverá um par de placas à esquerda e à direita do feixe, bem como um par de placas acima e abaixo do feixe, como na figura abaixo.

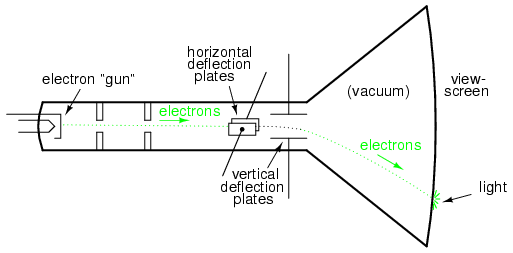
Tubo de raios catódicos (CRT) com placas de deflexão vertical e horizontal.



Se permitirmos que um sinal CA desvie o feixe para cima e para baixo (conecte essa fonte de tensão CA às placas de deflexão "verticais") e outro sinal CA desvie o feixe para a esquerda e para a direita (usando o outro par de placas de deflexão), os padrões ser produzido na tela do CRT indicativo da proporção dessas duas frequências AC.

Esses padrões são chamados de figuras de Lissajous e são um meio comum de medição comparativa de frequência em eletrônica.

Se as duas frequências forem iguais, obteremos uma figura simples na tela do CRT, a forma dessa figura sendo dependente da mudança de fase entre os dois sinais AC. Aqui está uma amostra das figuras de Lissajous para dois sinais de onda senoidal de igual frequência, mostrados como apareceriam na face de um osciloscópio (um instrumento de medição de tensão CA usando um CRT como seu “movimento”).

A primeira foto é da figura de Lissajous formada por duas tensões CA perfeitamente em fase uma com a outra:

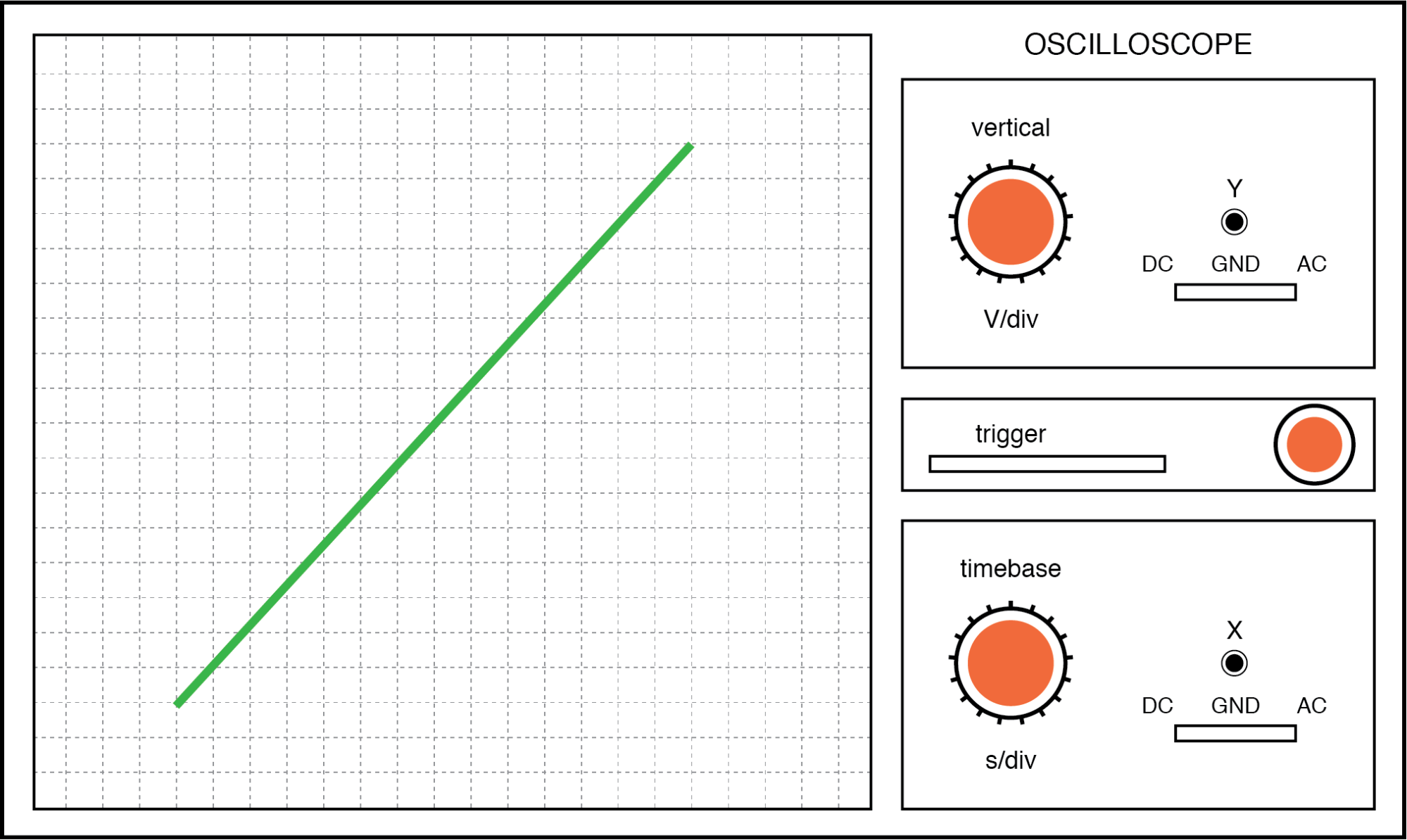
Figura de Lissajous:mesma frequência, mudança de fase de zero grau.



Se as duas tensões CA não estiverem em fase uma com a outra, uma linha reta não será formada. Em vez disso, a figura de Lissajous assumirá a aparência de uma oval, tornando-se perfeitamente circular se a mudança de fase for exatamente 90 ° entre os dois sinais e se suas amplitudes forem iguais:

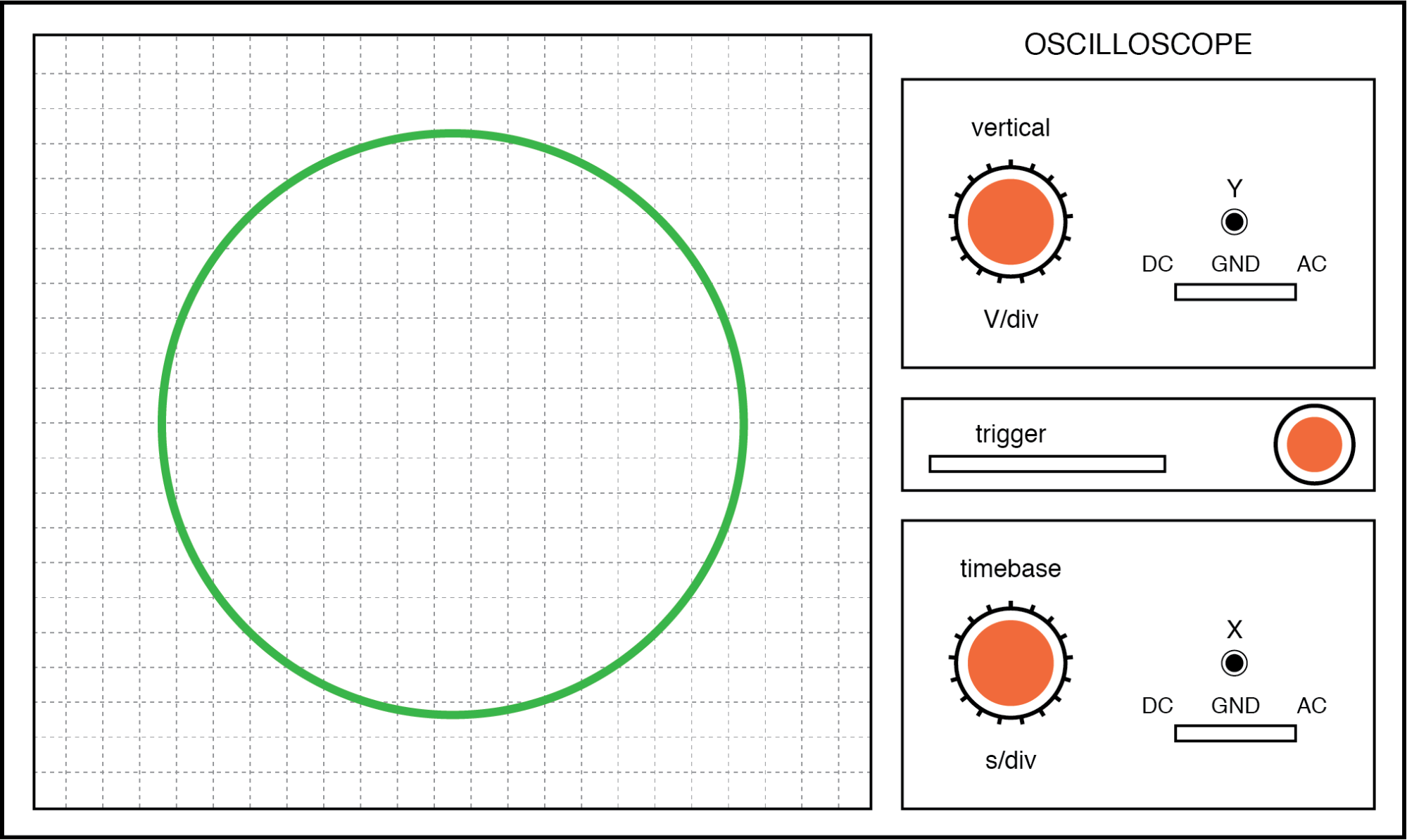
Figura de Lissajous:mesma frequência, mudança de fase de 90 ou 270 graus.



Finalmente, se os dois sinais AC estão diretamente opostos um ao outro em fase (deslocamento de 180 °), terminaremos com uma linha novamente, só que desta vez ela será orientada na direção oposta:

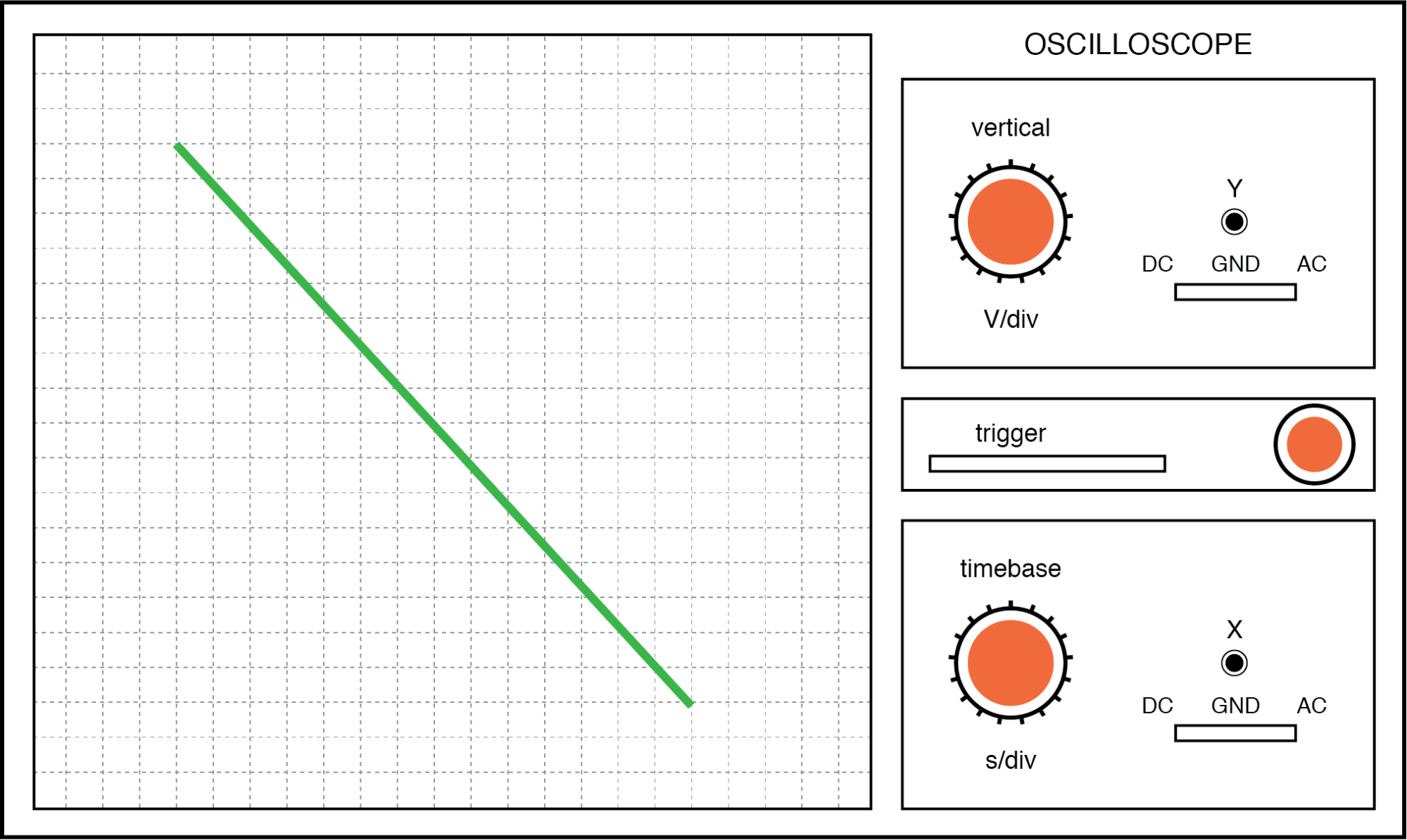
Figura de Lissajous:mesma frequência, deslocamento de fase de 180 graus.



Quando nos deparamos com frequências de sinal que não são iguais, os números de Lissajous ficam um pouco mais complexos. Considere os exemplos a seguir e eles recebem taxas de frequência vertical / horizontal:

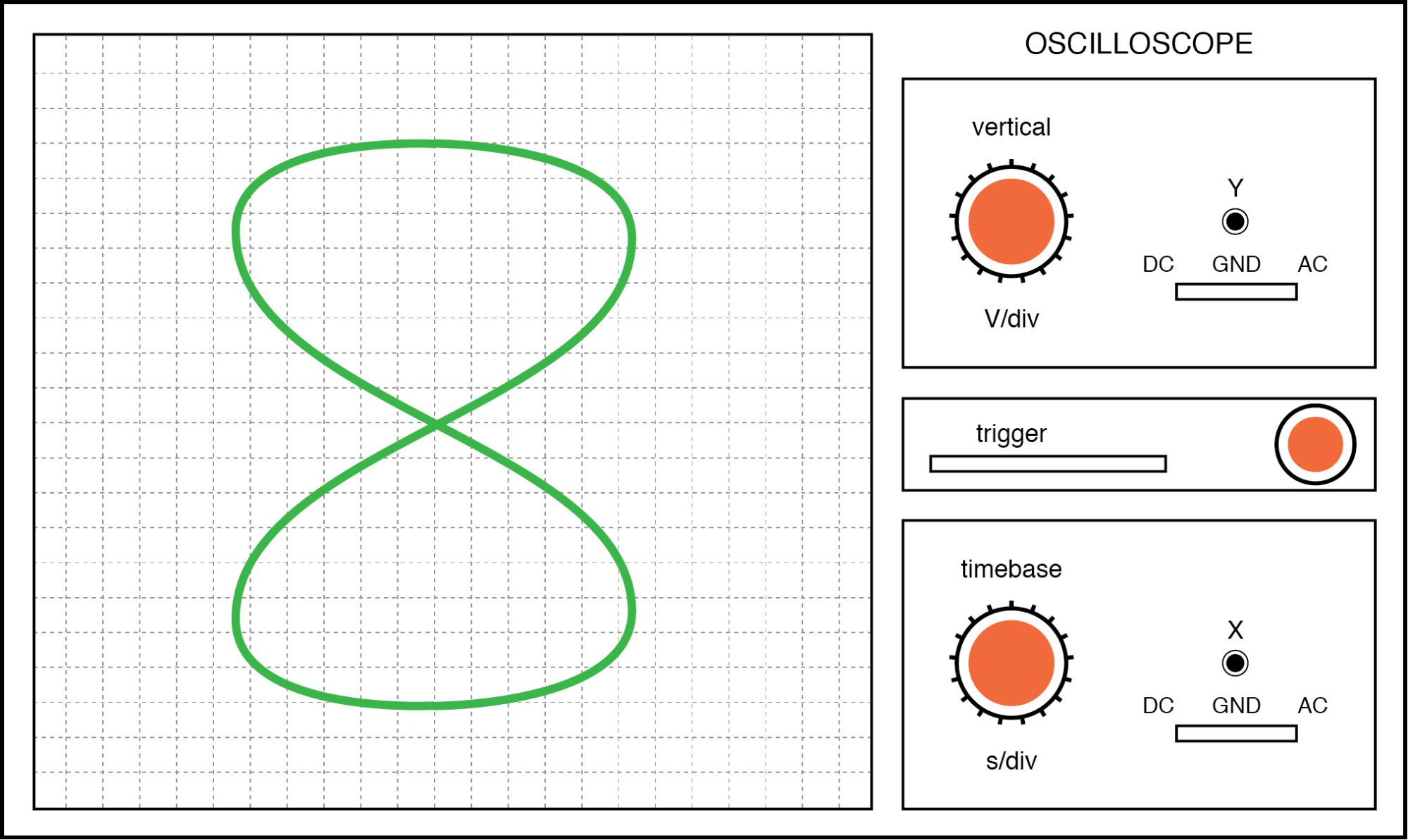
Figura de Lissajous:a frequência horizontal é o dobro da vertical.



Quanto mais complexa a razão entre as frequências horizontais e verticais, mais complexa é a figura de Lissajous. Considere a seguinte ilustração de uma razão de frequência de 3:1 entre horizontal e vertical:

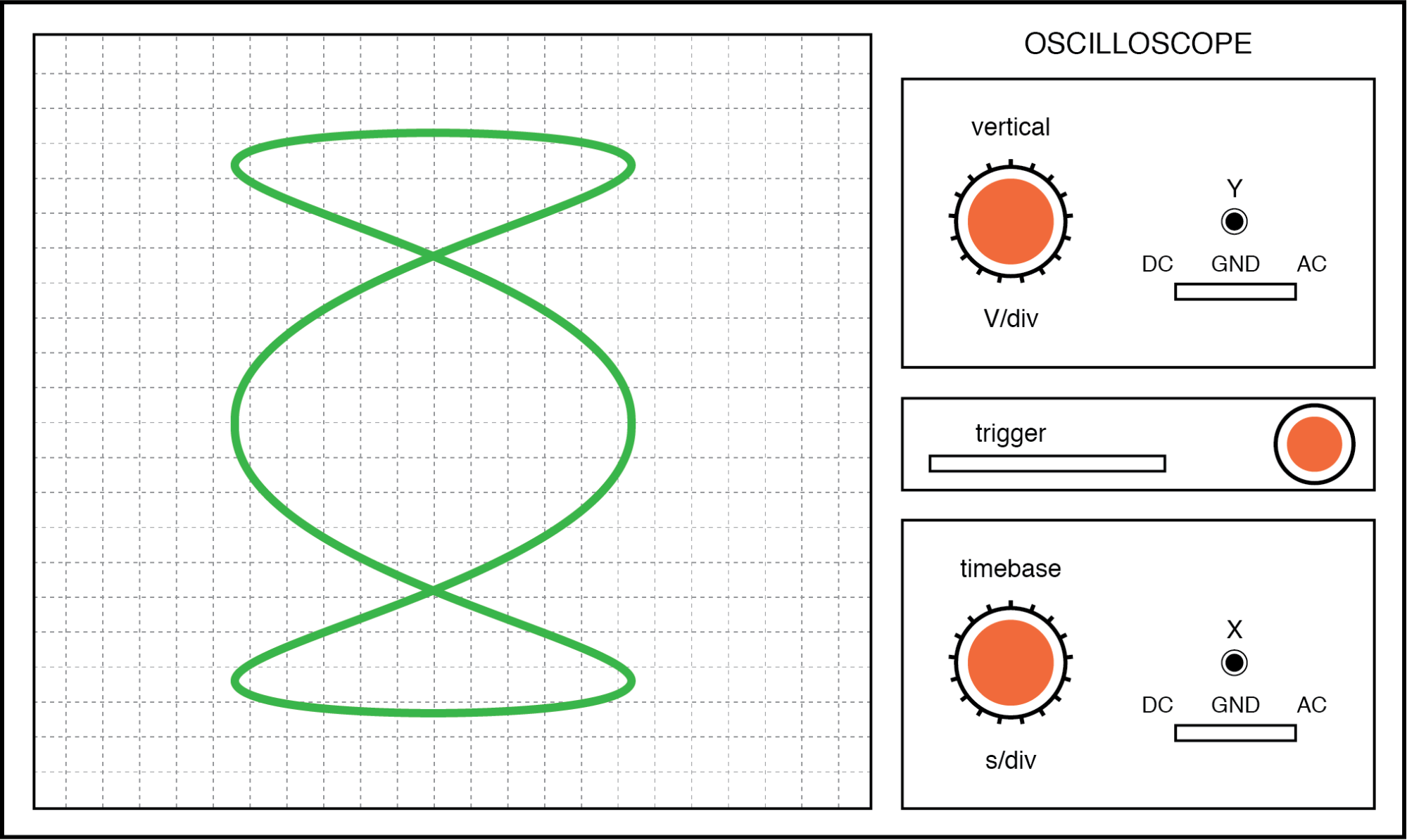
Figura de Lissajous:a frequência horizontal é três vezes maior que a vertical.



. . . e uma razão de frequência de 3:2 (horizontal =3, vertical =2) na figura abaixo.

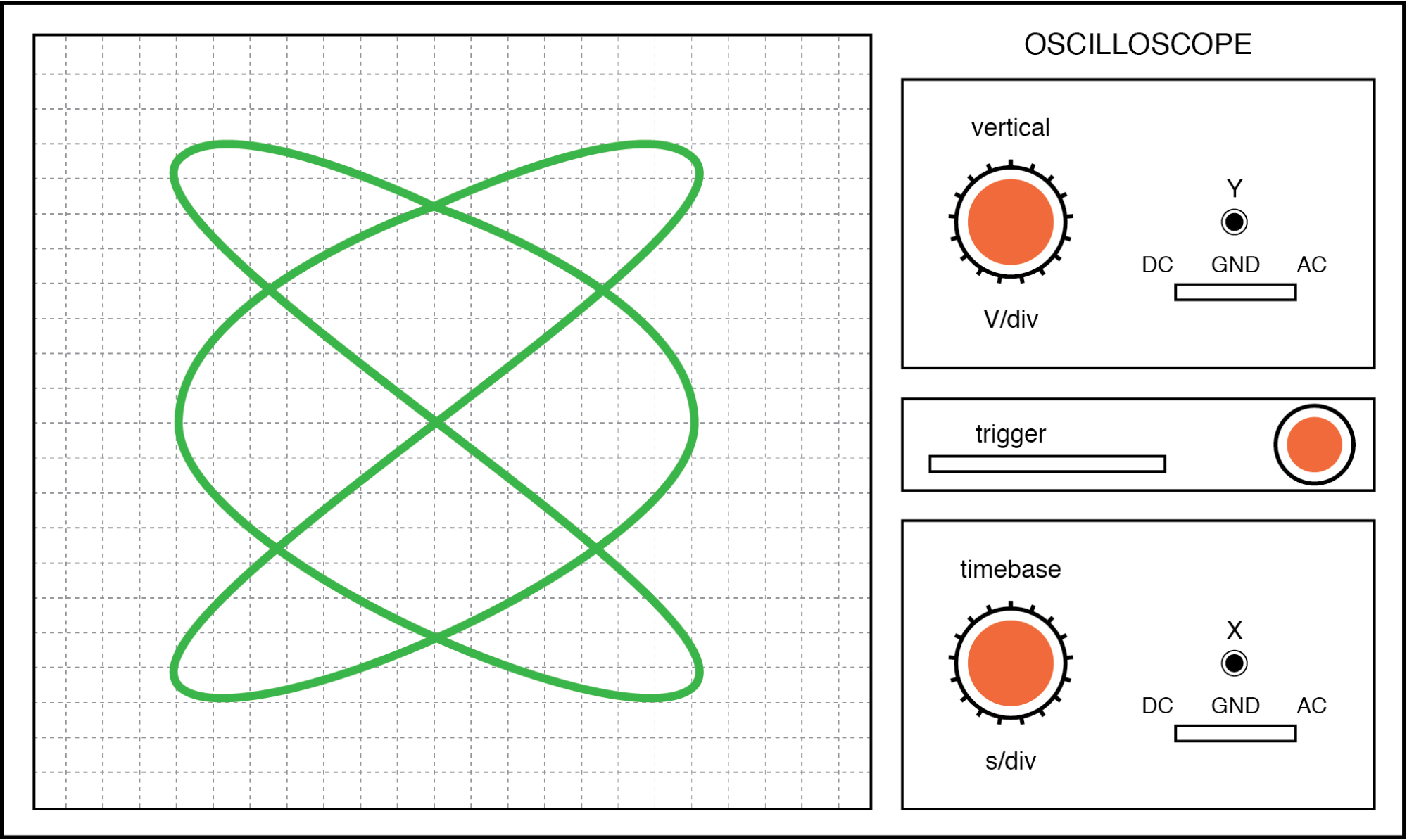
Figura de Lissajous:a relação de frequência horizontal / vertical é 3:2.



Nos casos em que as frequências dos dois sinais AC não são exatamente uma relação simples entre si (mas próximas), a figura de Lissajous parecerá "se mover", mudando lentamente a orientação conforme o ângulo de fase entre as duas formas de onda rola entre 0 ° e 180 °.

Se as duas frequências estiverem travadas em uma razão inteira exata entre si, a figura de Lissajous ficará estável na tela do CRT.

A física das figuras de Lissajous limita sua utilidade como uma técnica de comparação de frequência para casos em que as razões de frequência são valores inteiros simples (1:1, 1:2, 1:3, 2:3, 3:4, etc.).

Apesar desta limitação, os números de Lissajous são um meio popular de comparação de frequência onde quer que exista um padrão de frequência acessível (gerador de sinal).



REVER:

• Alguns medidores de frequência funcionam com base no princípio da ressonância mecânica, indicando a frequência por oscilação relativa entre um conjunto de "palhetas" exclusivamente sintonizadas e agitadas na frequência medida.
• Outros medidores de frequência usam circuitos ressonantes elétricos (circuitos tanque LC, geralmente) para indicar a frequência. Um ou ambos os componentes são feitos para serem ajustáveis, com um botão de ajuste calibrado com precisão e um medidor sensível é lido para tensão ou corrente máxima no ponto de ressonância.
• A frequência pode ser medida de forma comparativa, como é o caso ao usar um CRT para gerar figuras de Lissajous. Os sinais de frequência de referência podem ser feitos com um alto grau de precisão por circuitos osciladores usando cristais de quartzo como dispositivos ressonantes. Para ultra precisão, padrões de sinal de relógio atômico (com base nas frequências ressonantes de átomos individuais) podem ser usados.