Lei de Voltagem de Kirchhoff (KVL)
O que é a Lei de Voltagem de Kirchhoff (KVL)?
O princípio conhecido como Lei da Tensão de Kirchhoff (descoberto em 1847 por Gustav R. Kirchhoff, um físico alemão) pode ser declarado como tal:
“A soma algébrica de todas as tensões em um loop deve ser igual a zero”
Por algébrico , Quero dizer levando em conta os sinais (polaridades), bem como as magnitudes. Por loop , Refiro-me a qualquer caminho traçado de um ponto em um circuito até outros pontos nesse circuito e, finalmente, de volta ao ponto inicial.
Demonstrando a lei de tensão de Kirchhoff em um circuito em série
Vamos dar uma outra olhada em nosso circuito em série de exemplo, desta vez numerando os pontos no circuito para referência de tensão:
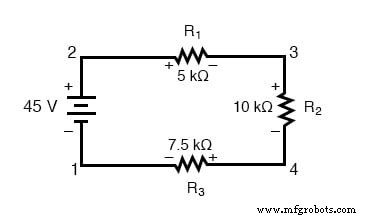
Se conectássemos um voltímetro entre os pontos 2 e 1, o cabo de teste vermelho ao ponto 2 e o cabo de teste preto ao ponto 1, o medidor registraria +45 volts. Normalmente, o sinal “+” não é mostrado, mas sim implícito, para leituras positivas em visores de medidores digitais. No entanto, para esta lição, a polaridade da leitura da tensão é muito importante e, portanto, mostrarei números positivos explicitamente:
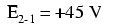
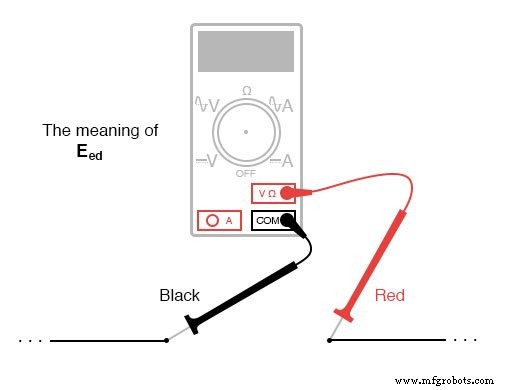
Quando uma tensão é especificada com um subscrito duplo (os caracteres “2-1” na notação “E 2-1 ”), Significa a tensão no primeiro ponto (2) medida em referência ao segundo ponto (1). Uma tensão especificada como “E cd ”Significaria a tensão indicada por um medidor digital com o cabo de teste vermelho no ponto“ c ”e o cabo de teste preto no ponto“ d ”:a tensão em“ c ”em referência a“ d ”.
Se pegássemos o mesmo voltímetro e medíssemos a queda de tensão em cada resistor, percorrendo o circuito no sentido horário com o cabo de teste vermelho do nosso medidor no ponto à frente e o cabo de teste preto no ponto atrás, obteríamos as seguintes leituras:
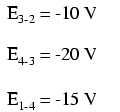
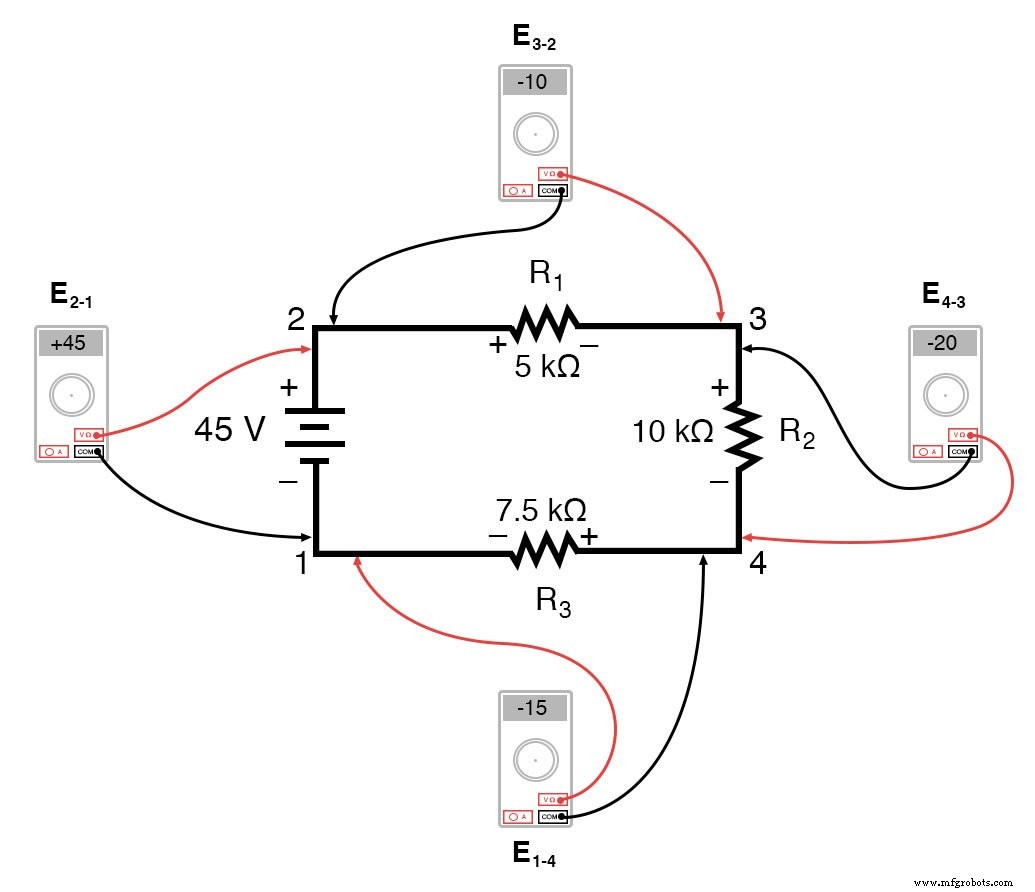
Já deveríamos estar familiarizados com o princípio geral para circuitos em série, afirmando que as quedas de tensão individuais somam a tensão total aplicada, mas medir as quedas de tensão dessa maneira e prestar atenção à polaridade (sinal matemático) das leituras revela outra faceta disso princípio:que as tensões medidas como tais somam zero:
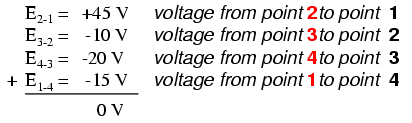
No exemplo acima, o loop foi formado pelos seguintes pontos nesta ordem:1-2-3-4-1. Não importa em que ponto começamos ou em que direção procedemos ao traçar o loop; a soma da tensão ainda será igual a zero. Para demonstrar, podemos calcular as tensões no circuito 3-2-1-4-3 do mesmo circuito:
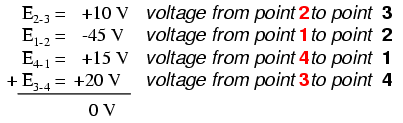
Isso pode fazer mais sentido se redesenharmos nosso circuito em série de exemplo para que todos os componentes sejam representados em uma linha reta:
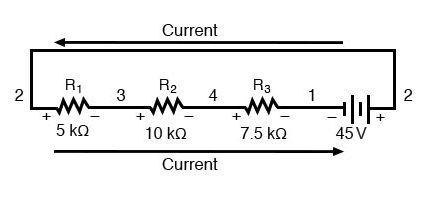
Ainda é o mesmo circuito em série, apenas com os componentes organizados de uma forma diferente. Observe as polaridades das quedas de tensão do resistor em relação à bateria:a tensão da bateria é negativa à esquerda e positiva à direita, enquanto todas as quedas de tensão do resistor são orientadas de outra forma:positiva à esquerda e negativa à direita. Isso ocorre porque os resistores estão resistindo o fluxo de carga elétrica sendo empurrado pela bateria. Em outras palavras, o “empurrão” exercido pelos resistores contra o fluxo de carga elétrica deve estar em uma direção oposta à fonte de força eletromotriz.
Aqui vemos o que um voltímetro digital indicaria em cada componente deste circuito, cabo preto à esquerda e cabo vermelho à direita, conforme disposto na horizontal:
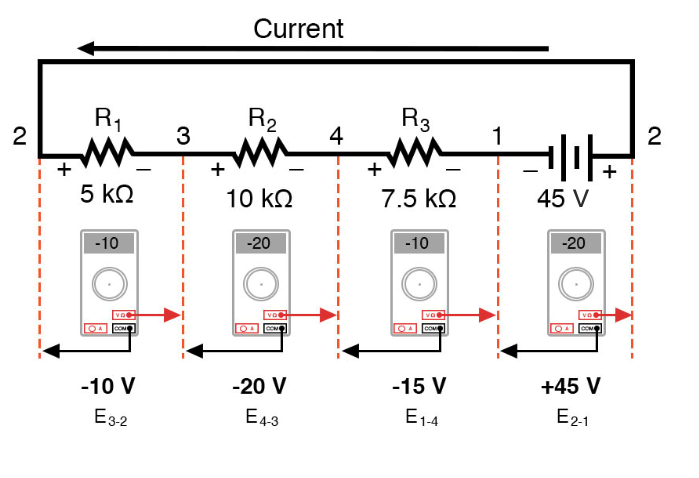
Se pegássemos o mesmo voltímetro e lêssemos a tensão nas combinações de componentes, começando com o único R 1 à esquerda e progredindo por toda a cadeia de componentes, veremos como as tensões somam algebricamente (para zero):
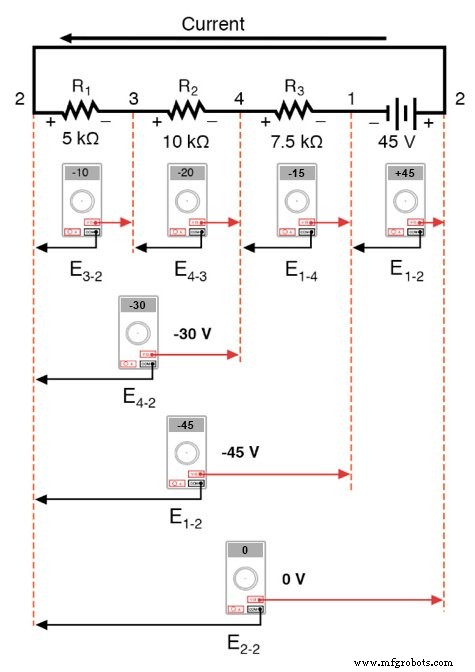
O fato de que as tensões em série aumentam não deve ser nenhum mistério, mas notamos que a polaridade dessas tensões faz muita diferença na soma dos números. Durante a leitura da tensão em R 1 —R 2 e R 1 —R 2 —R 3 (Estou usando um símbolo de “traço duplo” “-” para representar a série conexão entre resistores R 1 , R 2 e R 3 ), vemos como as tensões medem magnitudes sucessivamente maiores (embora negativas), porque as polaridades das quedas de tensão individuais estão na mesma orientação (esquerda positiva, direita negativa).
A soma das quedas de tensão em R 1 , R 2 e R 3 é igual a 45 volts, que é o mesmo que a saída da bateria, exceto que a polaridade da bateria é oposta às quedas de tensão do resistor (negativo à esquerda, positivo à direita), então terminamos com 0 volts medido em toda a cadeia de componentes.
Que deveríamos terminar com exatamente 0 volts em toda a corda também não deveria ser nenhum mistério. Olhando para o circuito, podemos ver que a extrema esquerda da string (lado esquerdo de R 1 :ponto número 2) é conectado diretamente à extrema direita da string (lado direito da bateria:ponto número 2), conforme necessário para completar o circuito.
Uma vez que esses dois pontos estão diretamente conectados, eles são eletricamente comuns um para o outro. E, como tal, a tensão entre esses dois pontos eletricamente comuns deve ser zero.
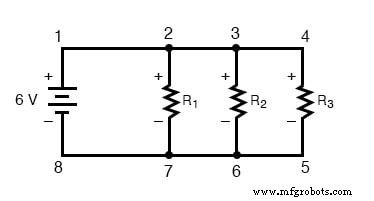
Demonstrando a lei de tensão de Kirchhoff em um circuito paralelo
Lei de Tensão de Kirchhoff (às vezes denotada como KVL para breve) funcionará para qualquer configuração de circuito em tudo, não apenas série simples. Observe como funciona para este circuito paralelo:
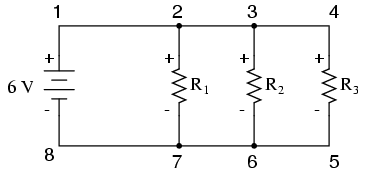
Sendo um circuito paralelo, a tensão em cada resistor é a mesma que a tensão de alimentação:6 volts. Calculando as tensões em torno do loop 2-3-4-5-6-7-2, obtemos:
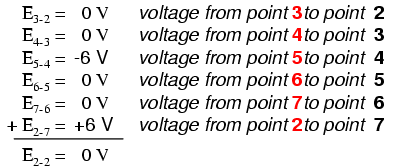
Observe como eu rotulo a tensão final (soma) como E 2-2 . Visto que começamos nossa sequência de passos de loop no ponto 2 e terminamos no ponto 2, a soma algébrica dessas tensões será a mesma que a tensão medida entre o mesmo ponto (E 2-2 ), que obviamente deve ser zero.
A validade da lei de tensão de Kirchhoff, independentemente da topologia do circuito
O fato de que este circuito é paralelo em vez de em série não tem nada a ver com a validade da Lei de Tensão de Kirchhoff. Por falar nisso, o circuito poderia ser uma "caixa preta" - sua configuração de componente completamente oculta de nossa visão, com apenas um conjunto de terminais expostos para medirmos a tensão entre - e KVL ainda seria verdadeiro:
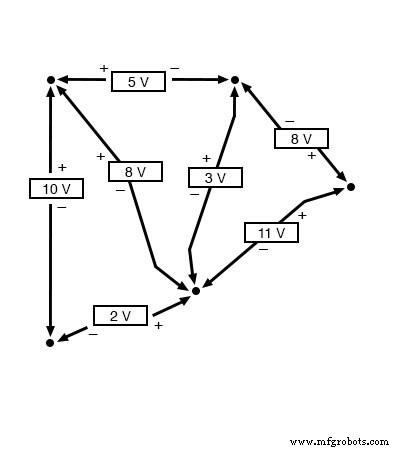
Tente qualquer ordem de etapas de qualquer terminal no diagrama acima, voltando para o terminal original, e você verá que a soma algébrica das tensões sempre é igual a zero.
Além disso, o "loop" que traçamos para KVL nem mesmo precisa ser um caminho de corrente real no sentido de circuito fechado da palavra. Tudo o que temos que fazer para cumprir o KVL é começar e terminar no mesmo ponto do circuito, calculando as quedas de tensão e polaridades à medida que avançamos entre o próximo e o último ponto. Considere este exemplo absurdo, rastreando “loop” 2-3-6-3-2 no mesmo circuito de resistor paralelo:
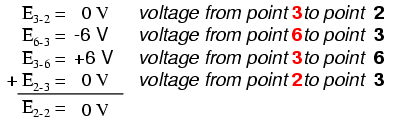
Usando a lei de tensão de Kirchhoff em um circuito complexo
KVL pode ser usado para determinar uma tensão desconhecida em um circuito complexo, onde todas as outras tensões em torno de um determinado “loop” são conhecidas. Pegue o seguinte circuito complexo (na verdade, dois circuitos em série unidos por um único fio na parte inferior) como exemplo:
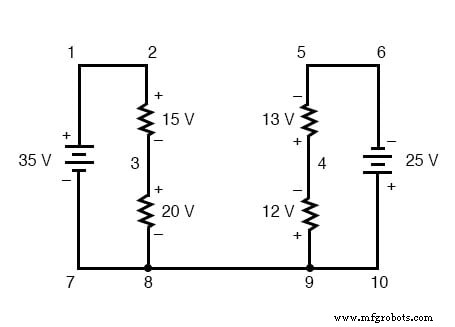
Para tornar o problema mais simples, omiti os valores de resistência e simplesmente dei quedas de tensão em cada resistor. Os dois circuitos da série compartilham um fio comum entre eles (fio 7-8-9-10), fazendo medições de tensão entre os dois circuitos possíveis. Se quiséssemos determinar a tensão entre os pontos 4 e 3, poderíamos configurar uma equação KVL com a tensão entre esses pontos como o desconhecido:
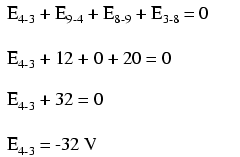
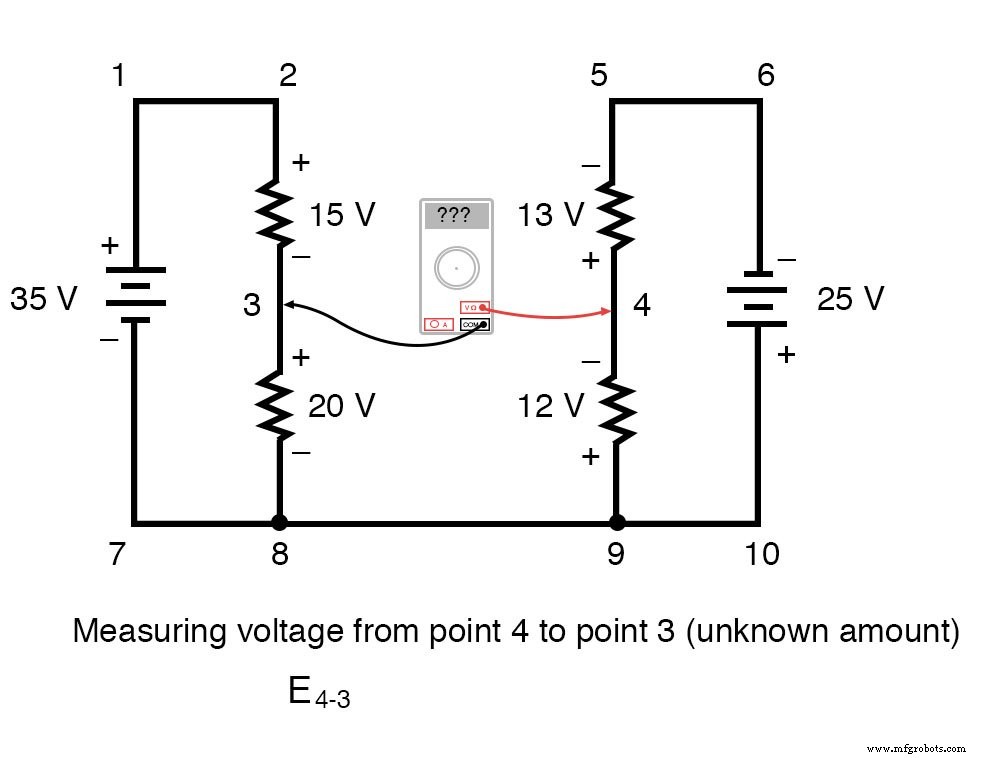
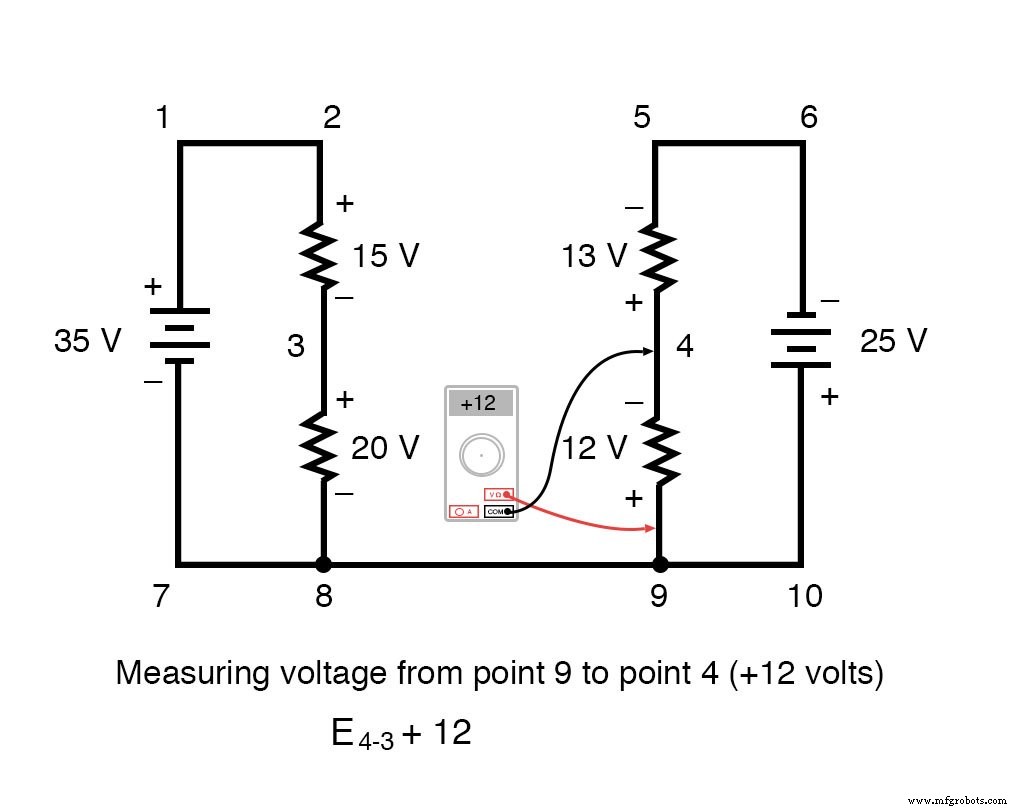
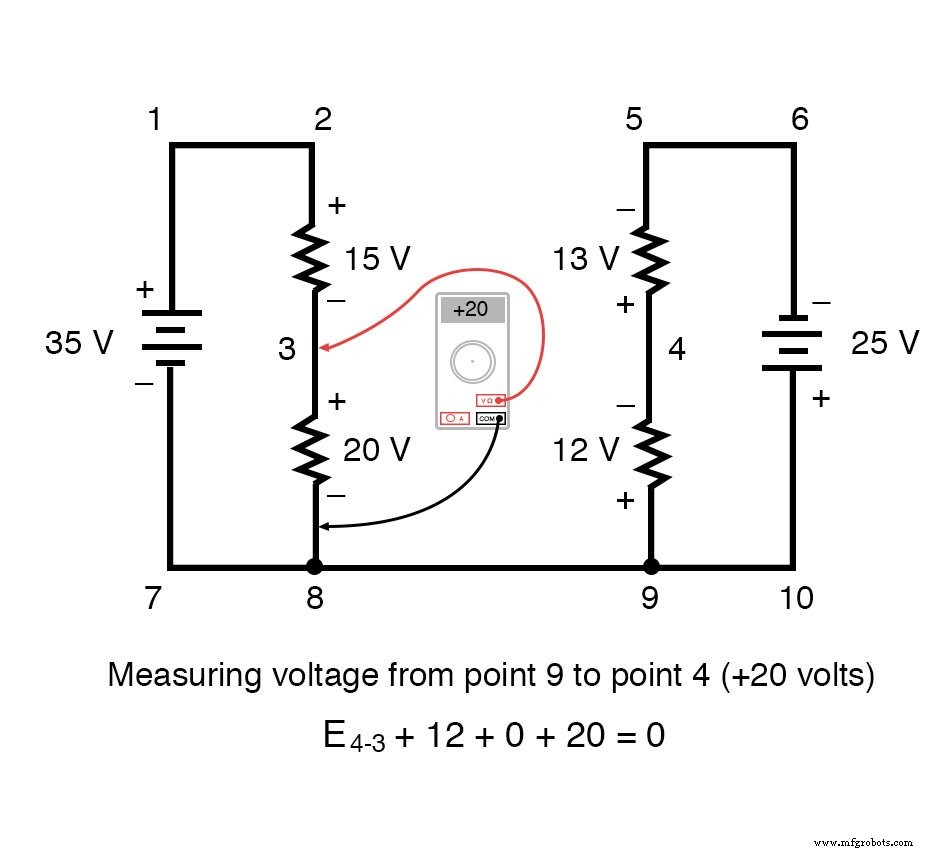
Percorrendo o circuito 3-4-9-8-3, escrevemos os valores da queda de tensão como um voltímetro digital os registraria, medindo com o cabo de teste vermelho no ponto à frente e o cabo de teste preto no ponto atrás à medida que avançamos o laço. Portanto, a tensão do ponto 9 ao ponto 4 é positiva (+) 12 volts porque o “cabo vermelho” está no ponto 9 e o “cabo preto” está no ponto 4.
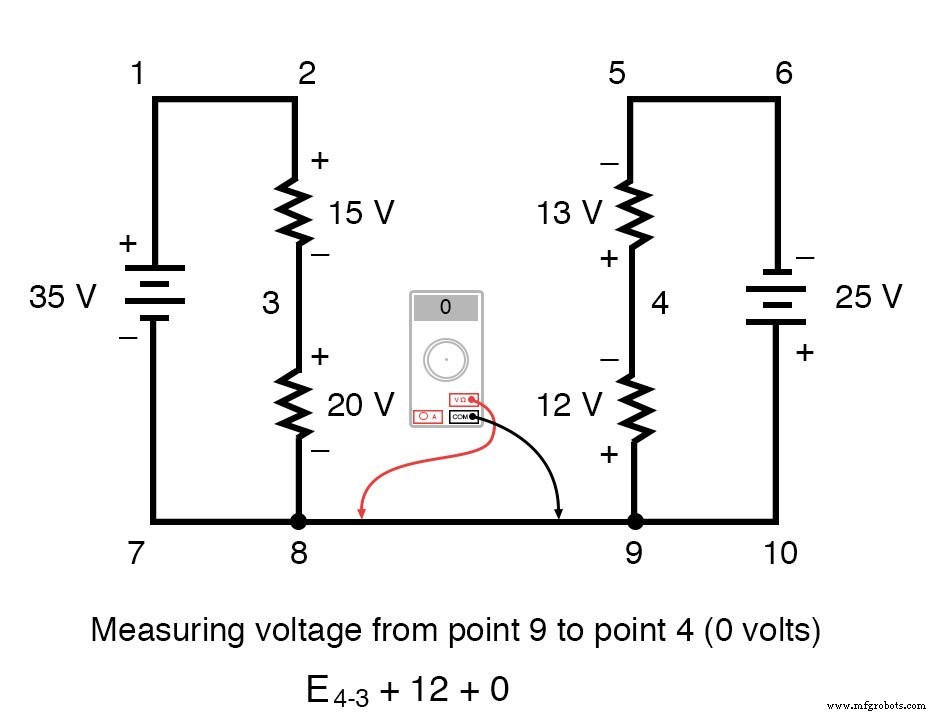
A tensão do ponto 3 ao ponto 8 é positiva (+) 20 volts porque o "cabo vermelho" está no ponto 3 e o "cabo preto" está no ponto 8. A tensão do ponto 8 ao ponto 9 é zero, é claro , porque esses dois pontos são eletricamente comuns.
Nossa resposta final para a tensão do ponto 4 ao ponto 3 é um negativo (-) 32 volts, nos dizendo que o ponto 3 é realmente positivo em relação ao ponto 4, exatamente o que um voltímetro digital indicaria com o fio vermelho no ponto 4 e o cabo preto no ponto 3:
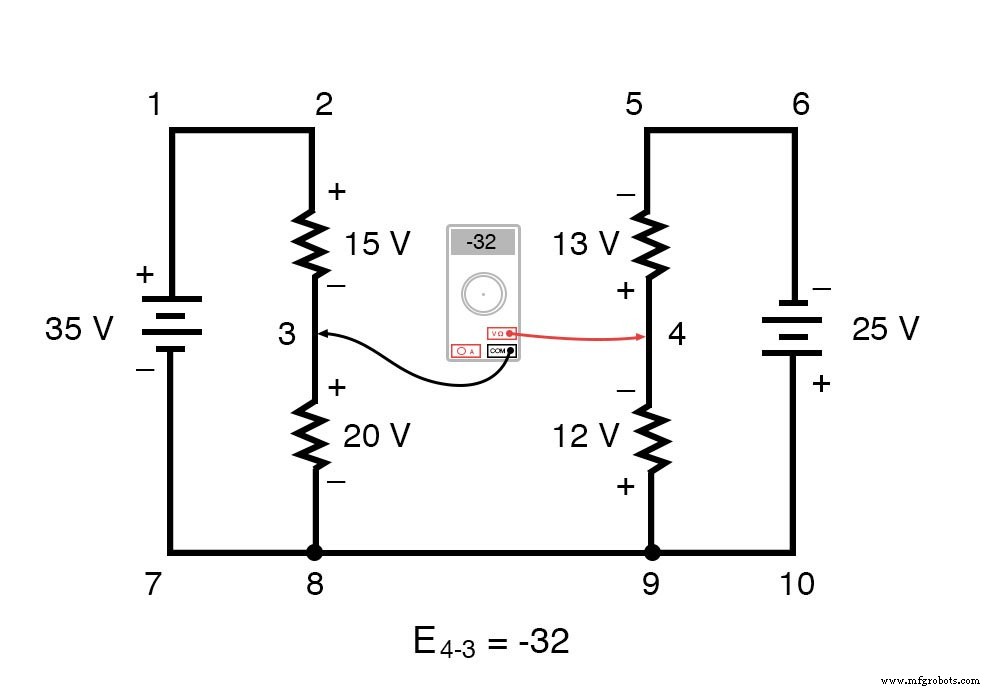
Em outras palavras, a colocação inicial de nossos "cabos de medição" neste problema KVL era "para trás". Se tivéssemos gerado nossa equação KVL começando com E 3-4 em vez de E 4-3 , percorrendo o mesmo loop com a orientação oposta do condutor do medidor, a resposta final seria E 3-4 =+32 volts:
É importante perceber que nenhuma das abordagens é "errada". Em ambos os casos, chegamos à avaliação correta da tensão entre os dois pontos, 3 e 4:o ponto 3 é positivo em relação ao ponto 4, e a tensão entre eles é de 32 volts.
REVER:
- Lei de tensão de Kirchhoff (KVL): “A soma algébrica de todas as tensões em um loop deve ser igual a zero”
PLANILHAS RELACIONADAS:
- Planilha de leis de Kirchhoff
Tecnologia industrial



