Lei da Corrente e Tensão de Kirchhoff (KCL &KVL) | Exemplo resolvido

KCL &KVL – Primeira e Segunda Leis de Kirchhoff com Exemplo Resolvido

Um físico alemão “Robert Kirchhoff” introduziu duas importantes leis elétricas em 1847 pelas quais podemos encontrar facilmente a resistência equivalente de uma rede complexa e correntes fluindo em diferentes condutores. Ambos os circuitos CA e CC podem ser resolvidos e simplificados usando essas leis simples que são conhecidas como Lei da Corrente de Kirchhoff (KCL) e Lei da Tensão de Kirchhoff (KVL).

Observe também que KCL é derivado da equação de continuidade de carga em eletromagnetismo, enquanto KVL é derivado da equação de Maxwell – Faraday para campo magnético estático (a derivada de B em relação ao tempo é 0 ).

Lei atual de Kirchhoff (KCL):

De acordo com a KCL:

Em qualquer rede elétrica, a soma algébrica das correntes de entrada para um ponto e das correntes de saída desse ponto é zero. Ou as correntes de entrada para um ponto são iguais às correntes de saída desse ponto.

Em outras palavras, a soma das correntes que fluem em direção a um ponto é igual à soma daquelas que se afastam dele. Ou a soma algébrica das correntes que entram em um nó é igual à soma algébrica das correntes que saem dele.

Explicação da KCL:

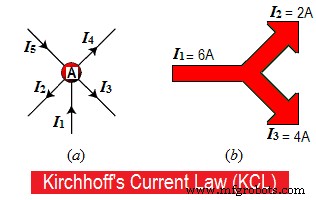
Suponha que alguns condutores estejam se encontrando em um ponto “A”, conforme mostrado na fig. 1.a. Em alguns condutores, as correntes estão entrando no ponto “A”, enquanto em outros condutores, as correntes estão saindo ou saindo do ponto “A”.

Considere as correntes de entrada ou entrada como “positivas (+) em direção ao ponto “A” enquanto as correntes de saída ou saída do ponto “A” são “negativas (-)”.
então:

Eu ₁ + (–eu ₂ ) + (–eu ₃ ) + (–eu ₄ ) + Eu ₅ =0

OU

Eu ₁ + Eu ₅ – Eu ₂ – Eu ₃ – Eu ₄ =0

OU

Eu ₁ + Eu ₅ =Eu ₂ + Eu ₃ + Eu ₄ =0

ou seja,

Correntes de entrada ou de entrada =Correntes de saída ou de saída

Ou

Σeu Inserindo =ΣI Saindo

Por exemplo, 8A está vindo em direção a um ponto e 5A mais 3A estão saindo desse ponto na fig 1.b, portanto,

8A =5A + 3A

8A =8A.

Lei de Tensão de Kirchhoff (KVL):

A segunda lei de Kirchhoff ou KVL afirmava que;

Em outras palavras, em qualquer malha fechada (que também é conhecida como Malha), a soma algébrica da EMF aplicada é igual à soma algébrica das quedas de tensão nos elementos . A segunda lei de Kirchhoff também é conhecida como lei da tensão ou lei da malha.

ΣIR=ΣE

Explicação do KVL:

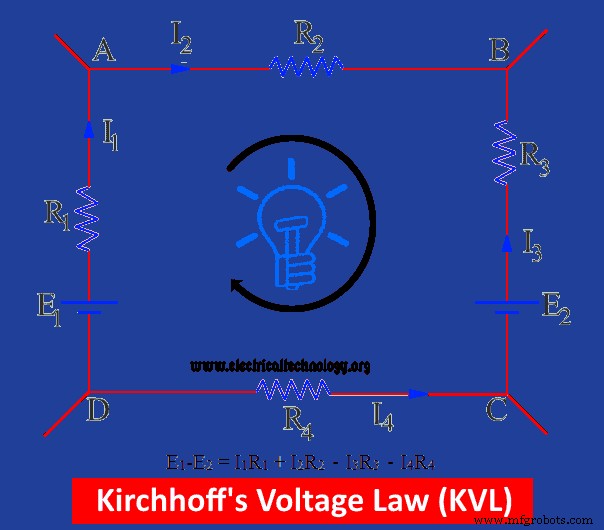
Um circuito fechado é mostrado na figura que contém duas conexões de baterias E₁ e E₂ . A soma total de E.M.Fs das baterias é indicada por E₁ -E₂ . A direção imaginária da corrente também é mostrada na fig.

E₁ conduz a corrente em tal direção que deve ser positiva enquanto E₂ interfere na direção da corrente (ou seja, está na direção oposta da suposta direção da corrente), portanto, é considerada negativa. A queda de tensão neste circuito fechado depende do produto de Tensão e Corrente.

A queda de tensão ocorre na suposta direção da corrente é conhecida como queda de tensão positiva enquanto a outra é queda de tensão negativa.

Na figura acima, eu₁ R₁ e eu₂ R₂ são quedas de tensão positivas e I₃ R₃ e eu₄ R₄ são V.D negativos.

Se percorrermos o circuito fechado (ou cada malha) e multiplicarmos a resistência do condutor e a corrente que flui nele, então a soma do IR é igual ao soma das fontes EMF aplicadas conectadas ao circuito.

A equação geral para o circuito acima é:

E₁ – E₂ =eu ₁ R₁ + eu ₂ R₂ – eu ₃ R₃ – eu ₄ R₄

Se formos na suposta direção da corrente como mostrado na figura, então o produto do IR é considerado positivo, caso contrário negativo.

É bom saber:

Direção da corrente:

É muito importante determinar a direção da corrente sempre que resolver circuitos através das leis de Kirchhoff. Igual ao caso da corrente eleitoral e corrente convencional.

A direção da corrente pode ser assumida no sentido horário ou anti-horário. Depois de selecionar a direção personalizada da corrente, você terá que aplicar e manter a mesma direção para todo o circuito até a solução final do circuito.

Se obtivermos o valor final como positivo significa que a suposta direção da corrente estava correta. Em caso de valores negativos, a corrente de sentido é invertida em relação à então suposta.

Análise de circuitos pelas leis de Kirchhoff

Exemplo resolvido em KCL e KVL (Leis de Kirchhoff)

Exemplo:

Resistores de R₁ =10Ω, R₂ =4Ω e R₃ =8Ω são conectadas até duas baterias (de resistência desprezível) conforme mostrado. Encontre a corrente através de cada resistor.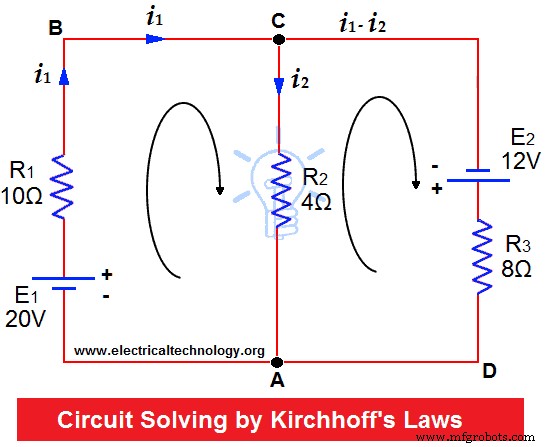

Solução:

Suponha que as correntes fluam nas direções indicadas pelas setas.

Aplicar KCL nas junções C e A.

Portanto, atual na malha ABC =i ₁

Atual em Mesh CA =i ₂

Então atual em Mesh CDA =i ₁ – eu ₂

Agora, aplique KVL na Malha ABC, 20V estão agindo no sentido horário. Igualando a soma dos produtos IR, temos;

10i ₁ + 4i ₂ =20   …   (1)

Na malha ACD, 12 volts estão agindo no sentido horário, então:

8(i ₁ – eu ₂ ) – 4i ₂ =12

8i ₁ – 8i ₂ – 4i ₂ =12

8i ₁ – 12i ₂ =12   …   (2)

Multiplicando a equação (1) por 3;

30i ₁ + 12i ₂ =60

Resolvendo para i ₁

30i ₁ + 12i ₂ =60

8i ₁ – 12i ₂ =12

___________
38i ₁ =72

A equação acima também pode ser simplificada pela Eliminação ou Regra de Cramer.

i ₁ =72 ÷ 38 =1,895 Amperes =Corrente no resistor de 10 Ohms

Substituindo este valor em (1), obtemos:

10 (1,895) + 4i ₂ =20

4i ₂ =20 - 18,95

i ₂ =0,263 Amperes =Corrente em Resistores de 4 Ohms.

Agora,

i ₁ – eu ₂ =1,895 – 0,263 =1,632 Ampères

Aplicações das Leis de Kirchhoff

• As leis de Kirchhoff podem ser usadas para determinar os valores de valores desconhecidos, como corrente e tensão, bem como a direção dos valores de fluxo desses quintetos no circuito.
• Essas leis podem ser aplicadas em qualquer circuito* (Veja a limitação das Leis de Kirchhoff no final do artigo), mas são úteis para encontrar os valores desconhecidos em circuitos e redes complexos.
• Também usado em análise Nodal e Mesh para encontrar os valores de corrente e tensão.
• A corrente através de cada loop independente é transportada aplicando KVL (cada loop) e corrente em qualquer elemento de um circuito contando toda a corrente (aplicável no método de corrente de loop).
l>
• A corrente através de cada ramificação é transportada aplicando KCL (cada junção) KVL em cada loop de um circuito (aplicável no método de corrente de loop).
• As Leis de Kirchhoff são úteis para entender a transferência de energia através de um circuito elétrico.

É bom saber:

Essas regras práticas devem ser levadas em consideração ao simplificar e analisar circuitos elétricos pelas Leis de Kirchhoff:

• A queda de tensão em um loop devido à corrente no sentido horário é considerada como queda de tensão positiva (+).
• A queda de tensão em um loop devido à corrente no sentido anti-horário é considerada como queda de tensão negativa (-).
• A corrente derivada da bateria no sentido horário é considerada positiva (+).
• A corrente derivada pela bateria no sentido anti-horário é considerada Positiva (-).

Limitações das leis de Kirchhoff:

• KCL é aplicável na suposição de que a corrente flui apenas em condutores e fios. Enquanto em circuitos de alta frequência, a capacitância parasita não pode mais ser ignorada. Nesses casos, a corrente pode fluir em um circuito aberto porque, nesses casos, condutores ou fios estão atuando como linhas de transmissão.
• KVL é aplicável na suposição de que não há campo magnético flutuante ligando o circuito fechado. Enquanto, na presença de mudança de campo magnético em circuitos CA de alta frequência, mas de comprimento de onda curto, o campo elétrico não é um campo vetorial conservativo. Assim, o campo elétrico não pode ser o gradiente de qualquer potencial e a integral de linha do campo elétrico ao redor da espira não é zero, contradizendo diretamente KVL. É por isso que o KVL não é aplicável em tal condição.
• Durante a transferência de energia do campo magnético para o campo elétrico, onde o fudge deve ser introduzido no KVL para tornar o P.d (diferenças de potencial) ao redor do circuito igual a 0.

Postagens relacionadas a teoremas de análise de circuitos elétricos:

• Teorema de Thevenin. Procedimento passo a passo com exemplo resolvido
• Teorema de Norton. Procedimento passo a passo fácil com exemplo (visualizações pictóricas)
• Análise de Circuitos SUPERNÓDEOS | Passo a passo com exemplo resolvido
• Análise de Circuitos SUPERMESH | Passo a passo com exemplo resolvido
• Teorema de Transferência de Potência Máxima para Circuitos CA e CC
• Teorema da Compensação – Demonstração, Explicação e Exemplos Resolvidos
• Teorema da Substituição – Guia Passo a Passo com Exemplo Resolvido
• Teorema de Millman – Analisando circuitos CA e CC – Exemplos
• Teorema da Superposição – Análise de Circuitos com Exemplo Resolvido
• Teorema de Tellegen – Exemplos Resolvidos e Simulação MATLAB
• Regra do divisor de tensão (VDR) – Exemplos resolvidos para circuitos R, L e C
• Regra do divisor atual (CDR) – Exemplos resolvidos para circuitos CA e CC
• Lei de Ohm:Explicação simples com declarações e fórmulas
• Estrela para Delta e Delta para Estrela. Transformação Y-Δ