Método de tensão do nó

O método de análise de tensão de nó resolve tensões desconhecidas em nós de circuito em termos de um sistema de equações KCL. Esta análise parece estranha porque envolve a substituição de fontes de tensão por fontes de corrente equivalentes. Além disso, os valores do resistor em ohms são substituídos por condutâncias equivalentes em siemens, G =1 / R. O siemens (S) é a unidade de condutância, tendo substituído a unidade mho. Em qualquer caso, S =Ω-1. E S =mho (obsoleto).

Método para cálculo da tensão do nó

Começamos com um circuito com fontes de tensão convencionais. Um nó comum E ₀ é escolhido como ponto de referência. As tensões do nó E ₁ e E ₂ são calculados em relação a este ponto.





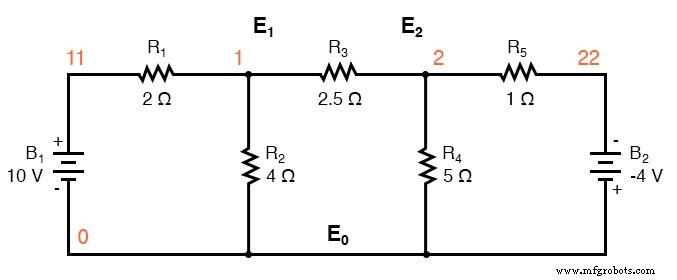
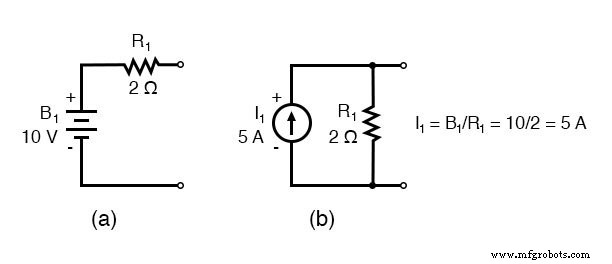
Substituir fontes de tensão e resistores em série associados por fontes de corrente equivalentes e resistores paralelos produz o circuito modificado. Substitua as condutâncias do resistor em siemens pela resistência em ohms.

 I1 =E1 / R1 =10/2 =5 A I2 =E2 / R5 =4/1 =4 A G1 =1 / R1 =1/2 Ω =0,5 S G2 =1 / R2 =1/4 Ω =0,25 S G3 =1 / R3 =1 / 2,5 Ω =0,4 S G4 =1 / R4 =1/5 Ω =0,2 S G5 =1 / R5 =1/1 Ω =1,0 S 

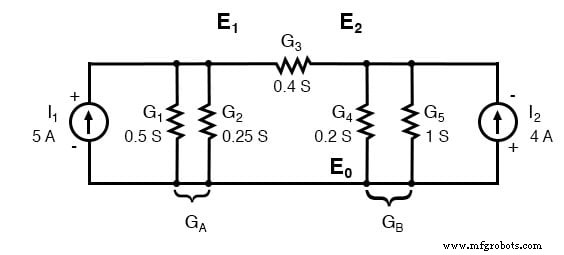
As condutâncias paralelas (resistências) podem ser combinadas pela adição das condutâncias. Porém, não vamos redesenhar o circuito. O circuito está pronto para a aplicação do método da tensão do nó.

 GA =G1 + G2 =0,5 S + 0,25 S =0,75 S GB =G4 + G5 =0,2 S + 1 S =1,2 S 

Derivando um método geral de voltagem de nó, escrevemos um par de equações KCL em termos de voltagens de nó desconhecidas V ₁ e V ₂ desta vez. Fazemos isso para ilustrar um padrão para escrever equações por inspeção.

 GAE1 + G3 (E1 - E2) =I1 (1) GBE2 - G3 (E1 - E2) =I2 (2) (GA + G3) E1 -G3E2 =I1 (1) -G3E1 + (GB + G3) E2 =I2 (2) 

Os coeficientes do último par de equações acima foram reorganizados para mostrar um padrão. A soma das condutâncias conectadas ao primeiro nó é o coeficiente positivo da primeira tensão na equação (1). A soma das condutâncias conectadas ao segundo nó é o coeficiente positivo da segunda tensão na equação (2). Os outros coeficientes são negativos, representando condutâncias entre os nós. Para ambas as equações, o lado direito é igual à respectiva fonte de corrente conectada ao nó. Esse padrão nos permite escrever rapidamente as equações por inspeção. Isso leva a um conjunto de regras para o método de análise da tensão do nó.

Regras de tensão do nó:

• Converta fontes de tensão em série com um resistor em uma fonte de corrente equivalente com o resistor em paralelo.
• Altere os valores do resistor para condutâncias.
• Selecione um nó de referência (E ₀ )
• Atribuir tensões desconhecidas (E ₁ ) (E ₂ ) ... (E _N ) para os nós restantes.
• Escreva uma equação KCL para cada nó 1,2, ... N. O coeficiente positivo da primeira tensão na primeira equação é a soma das condutâncias conectadas ao nó. O coeficiente para a segunda tensão na segunda equação é a soma das condutâncias conectadas a esse nó. Repita para o coeficiente da terceira tensão, terceira equação e outras equações. Esses coeficientes caem na diagonal.
• Todos os outros coeficientes para todas as equações são negativos, representando condutâncias entre os nós. A primeira equação, o segundo coeficiente é a condutância do nó 1 ao nó 2, o terceiro coeficiente é a condutância do nó 1 ao nó 3. Preencha os coeficientes negativos para outras equações.
• O lado direito das equações é a fonte atual conectada aos respectivos nós.
• Resolva o sistema de equações para tensões de nó desconhecidas.

Exemplo de método de tensão do nó

Exemplo: Configure as equações e resolva as tensões dos nós usando os valores numéricos da figura acima.

Solução:

 (0,5 + 0,25 + 0,4) E1 - (0,4) E2 =5 - (0,4) E1 + (0,4 + 0,2 + 1,0) E2 =-4 (1,15) E1 - (0,4) E2 =5 - (0,4) E1 + (1,6) E2 =-4 E1 =3,8095 E2 =-1,5476 

A solução de duas equações pode ser realizada com uma calculadora ou com uma oitava (não mostrada). A solução é verificada com SPICE com base no diagrama esquemático original com fontes de tensão. Porém, o circuito com as fontes de corrente poderia ter sido simulado.

 V1 11 0 DC 10 V2 22 0 DC -4 r1 11 1 2 r2 1 0 4 r3 1 2 2,5 r4 2 0 5 r5 2 22 1 .DC V1 10 10 1 V2 -4 -4 1 .imprimir DC V (1) V (2) .fim v (1) v (2) 3,809524e + 00 -1,547619e + 00 

Mais um exemplo. Este possui três nós. Não listamos as condutâncias no diagrama esquemático. No entanto, G ₁ =1 / R ₁ etc.



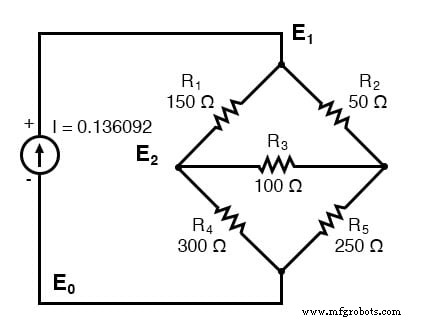
Existem três nós para escrever equações para inspeção. Observe que os coeficientes são positivos para a equação (1) E ₁ , equação (2) E ₂ , e equação (3) E ₃ . Essas são as somas de todas as condutâncias conectadas aos nós. Todos os outros coeficientes são negativos, representando uma condutância entre os nós. O lado direito das equações é a fonte de corrente associada, 0,136092 A para a única fonte de corrente no nó 1. As outras equações são zero no lado direito por falta de fontes de corrente. Somos muito preguiçosos para calcular as condutâncias para os resistores no diagrama. Assim, os G subscritos são os coeficientes.

 (G1 + G2) E1 -G1E2 -G2E3 =0,136092 -G1E1 + (G1 + G3 + G4) E2 -G3E3 =0 -G2E1 -G3E2 + (G2 + G3 + G5) E3 =0 

Somos tão preguiçosos que inserimos resistências recíprocas e somas de resistências recíprocas na matriz de oitava “A”, permitindo que a oitava calcule a matriz de condutâncias após “A =”. A linha de entrada inicial era tão longa que foi dividida em três linhas. Isso é diferente dos exemplos anteriores. A matriz “A” inserida é delineada iniciando e terminando os colchetes. Os elementos da coluna são separados por espaço. As linhas são separadas por “nova linha”. Vírgulas e pontos-e-vírgulas não são necessários como separadores. Porém, o vetor atual em “b” é separado por ponto e vírgula para produzir um vetor coluna de correntes.

 oitava:12> A =[1/150 + 1/50 -1/150 -1/50> -1/150 1/150 + 1/100 + 1/300 -1/100> -1/50 -1/100 1/50 + 1/100 + 1/250] A =0,0266667 -0,0066667 -0,0200000 -0,0066667 0,0200000 -0,0100000 -0,0200000 -0,0100000 0,0340000 oitava:13> b =[0,136092; 0; 0] b =0,13609 0,00000 0,00000 oitava:14> x =A \ b x =24.000 17,655 19,310 

Observe que os coeficientes diagonais da matriz “A” são positivos, que todos os outros coeficientes são negativos.

A solução como um vetor de tensão está em “x”. E ₁ =24.000 V, E ₂ =17,655 V, E ₃ =19,310 V. Essas três tensões se comparam à corrente da malha anterior e às soluções SPICE do problema da ponte desequilibrada. Isso não é coincidência, pois a fonte de corrente 0,13609 A foi escolhida propositalmente para produzir os 24 V usados ​​como fonte de tensão naquele problema.

Resumo

• Dada uma rede de condutâncias e fontes de corrente, o método de análise de circuito de tensão de nó resolve para tensões de nó desconhecidas a partir de equações KCL.
• Consulte as regras acima para obter detalhes sobre como escrever as equações por inspeção.
• A unidade de condutância G é o siemens S. A condutância é o recíproco da resistência:G =1 / R

PLANILHAS RELACIONADAS:

• Planilha de circuitos precisos de diodo
• Folha de trabalho das leis de Kirchhoff