Análise de circuito SUPERMESH | Passo a passo com exemplo resolvido

Supermesh  Análise – Declaração , Fórmula, Exemplos Resolvidos

O que é análise de supermalha?

Análise de supermalha ou supermalha é uma técnica melhor em vez de usar a análise de malha para analisar um circuito ou rede elétrica tão complexa, onde duas malhas têm uma fonte de corrente como elemento comum. É o mesmo quando usamos análise de circuitos de supernós em vez de análise de nós ou circuitos nodais para simplificar tal rede onde o supernó atribuído, encerrando totalmente a fonte de tensão dentro do supernó e reduzindo o número de nós sem referência em um (1) para cada fonte de tensão.

Na técnica de análise de circuitos de supermalha, a fonte de corrente está na área interna da supermalha. Portanto, podemos reduzir o número de malhas em uma (1) para cada fonte de corrente presente no circuito.

A malha simples pode ser ignorada, se a fonte de corrente (nessa malha) estiver no perímetro do circuito. Alternativamente, KVL (Lei de Tensão de Kirchhoff) é aplicada apenas às malhas ou supermalhas do circuito renovado.

A propósito, é difícil entender pelo Preâmbulo, então primeiro vamos resolver um circuito simples por análises de circuitos de supermalha e, em seguida, resumiremos toda a análise de supermalha (etapa por passo).

• Post relacionado:Análise de circuito SUPERNODE | Passo a passo com exemplo resolvido

Exemplo resolvido de análise de supermalha

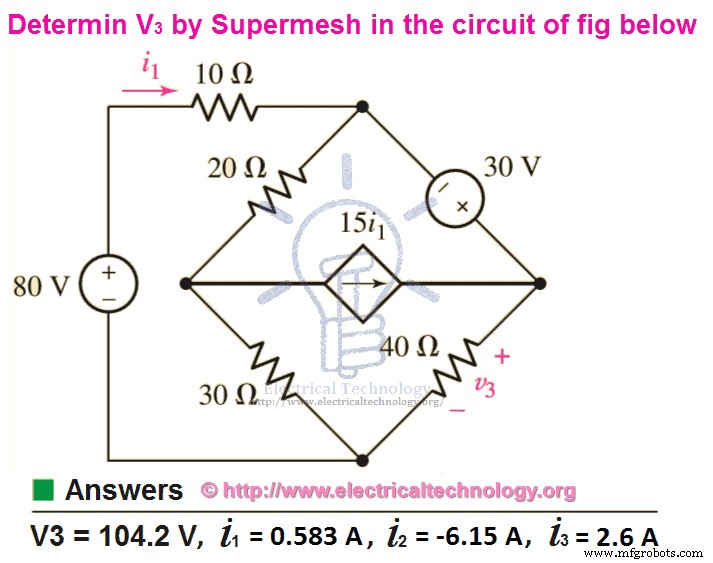
Exemplo:

Use a análise de malha para encontrar V₃ e i atual ₁ , e ₂ e eu ₃ na figura a seguir?

Solução:

Usando KVA na malha 1.

80 =10i ₁ + 20(eu ₁ –  eu ₂ ) + 30 (eu ₁ – e₃ )

Simplificando

80 =10i ₁ + 20i ₁ –  20eu ₂ + 30i ₁ – 30eu ₃

80 =60i ₁ – 20i ₂ –  30eu ₃ ...... → Eq 1.

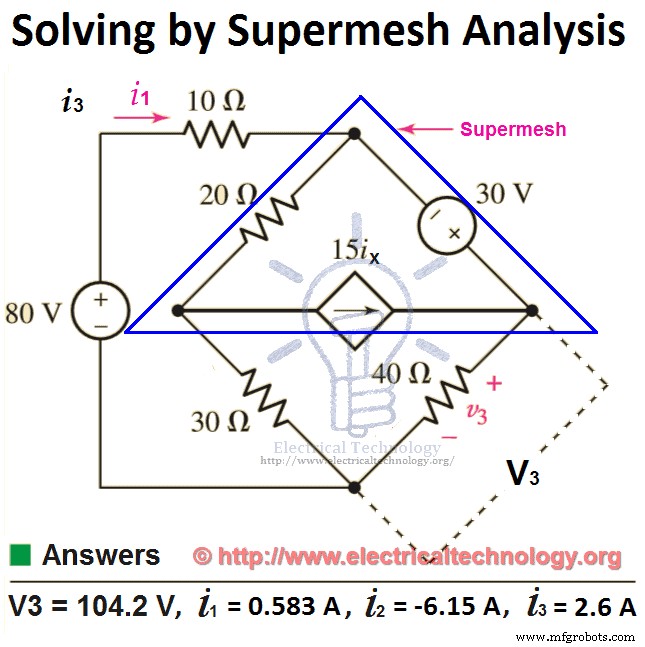
Agora aplique KVL em Supermesh (que é a integração da malha 2 e malha 3 , mas nós o reduzimos por uma malha simples que é conhecida como supermalha )

30 =40i ₃ + 30(eu ₃ – eu ₁ ) +20(eu ₂ – eu ₁ )

30 =40i ₃ + 30i ₃ – 30eu ₁ + 20i ₂ – 20eu ₁

30 =70i ₃ – 50i ₁ + 20i ₂ ….. → Eq 2.

Mas aqui, temos três (3) variáveis, ou seja, i 1, eu 2 e eu 3. E há duas equações. Portanto, precisamos também de três equações.

A fonte atual independente (na supermalha ) está relacionado com as correntes de malha assumidas, ou seja,

15i x =eu ₃ – eu ₂

i ₃ =15i x + eu ₂ ….. → Eq 3.

Resolver as equações 1, 2 e 3 pela regra de Cramer ou Cramer calculadora de regras , Eliminação , Eliminação de Gauss ou programa assistido por computador como MATLAB , nós achamos

i ₁ =0,583A

i ₂ =-6,15A

i ₃ =2,6A

Além disso, podemos encontrar o valor de V₃ ,

V₃ =eu ₃ x R₃

Colocando os valores,

V₃ =2,6A x 40Ω

V₃ =104 V.

Resumo da análise de supermalha (passo a passo)

1. Avalie se o circuito é um circuito plano . se sim, aplique Supermesh. Se não, execute a análise nodal.
2. Redesenhe o circuito se necessário e conte o número de malhas no circuito.
3. Etiquete cada uma das correntes de malha no circuito . Como regra geral, definir todas as correntes de malha para fluir no sentido horário resulta em uma análise de circuito mais simples.
4. Forme uma supermalha se o circuito contiver fontes de corrente por duas malhas . Assim, a supermalha envolveria ambas as malhas.
5. Escreva um KVL ( Kirchhoff Lei da tensão) em torno de cada malha e supermalha no circuito . Comece com um nó fácil e ajustado. Agora prossiga na direção da corrente de malha. Pegue o sinal “-“ na conta enquanto escreve as equações KVL e resolve o circuito. Nenhuma equação KVL é necessária se uma fonte de corrente estiver na periferia de uma malha. Assim, a corrente de malha é determinada e avaliada por inspeção.
6. Uma KCL (Lei da Corrente de Kirchhoff) é necessária para cada supermalha definida e pode ser realizada pela simples aplicação da KCL. em palavras simples, relacione a corrente que flui de cada fonte de corrente com as correntes de malha.
7. Um caso adicional pode ocorrer se o circuito contiver outras fontes dependentes. Nesse caso, expresse quaisquer valores e quantidades desconhecidos adicionais, como correntes ou tensões diferentes das correntes de malha, em termos de correntes de malha adequadas.
8. Organize e organize o sistema de equações.
9. Por fim, resolva o sistema de equações para as tensões nodais como V₁ , V₂ , e V₃ etc. haverá Mesh deles. se você encontrar dificuldades para resolver o sistema de equações, consulte o exemplo acima.

Postagens relacionadas:

• Teorema de Thévenin. Procedimento passo a passo com exemplo resolvido
• Teorema de Norton. Procedimento passo a passo fácil com exemplo (visualizações pictóricas)
• Lei de Ohm:explicação simples com declarações e fórmulas
• Teorema de transferência de potência máxima para circuitos CA e CC
• Lei de Corrente e Tensão de Kirchhoff (KCL e KVL) | Exemplo resolvido
• Teorema da Compensação - Demonstração, Explicação e Exemplos Resolvidos
• Teorema da Substituição – Guia Passo a Passo com Exemplo Resolvido
• Teorema de Millman – Análise de circuitos CA e CC – Exemplos
• Teorema da Superposição - Análise de Circuito com Exemplo Resolvido
• Teorema de Tellegen - Exemplos Resolvidos e Simulação MATLAB
• Regra do divisor de tensão (VDR) - Exemplos resolvidos para circuitos R, L e C
• Regra do divisor de corrente (CDR) – Exemplos resolvidos para circuitos CA e CC
• Conversão de Estrela para Delta e Delta para Estrela. Transformação Y-Δ