Derivadas das funções de poder de e

Exemplos de derivados de e

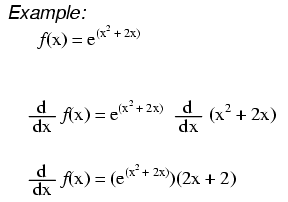
Constante de proporcionalidade

Quando dizemos que uma relação ou fenômeno é “exponencial”, estamos sugerindo que alguma quantidade - corrente elétrica, lucros, população - aumenta mais rapidamente à medida que a quantidade aumenta. Em outras palavras, a taxa de mudança em relação a uma determinada variável é proporcional ao valor dessa variável. Isto significa que a derivada de uma função exponencial é igual à função exponencial original multiplicada por uma constante ( k ) que estabelece a proporcionalidade.

$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =ka ^ x $$

A constante de proporcionalidade é igual ao logaritmo natural da base do expoente:

$$ \ frac {\ text {d}} {\ text {d} x} a ^ x =\ ln (a) \ vezes a ^ x $$

Segue-se, então, que se o logarítmico natural da base for igual a um, a derivada da função será igual à função original. Isso é exatamente o que acontece com as funções de potência de e:o logarítmico natural de e é 1 e, conseqüentemente, a derivada de $$ e ^ x $$ é $$ e ^ x $$.

$$ \ frac {\ text {d}} {\ text {d} x} e ^ x =e ^ x $$

A regra da "corrente"

Quando a expressão exponencial é algo diferente de simplesmente x, aplicamos a regra da cadeia:primeiro, pegamos a derivada de toda a expressão e, em seguida, a multiplicamos pela derivada da expressão no expoente.

$$ \ frac {\ text {d}} {\ text {d} x} e ^ {x ^ 2 + 2x} =e ^ {x ^ 2 + 2x} \ times \ frac {\ text {d}} { \ text {d} x} (x ^ 2 + 2x) =(2x + 2) e ^ {x ^ 2 + 2x} $$

Esta técnica pode ser usada para encontrar a taxa de variação da corrente do diodo em relação à tensão do diodo. A seguinte equação fornece uma relação aproximada entre a tensão em um diodo ($$ V_D $$) e a corrente em um diodo ($$ I_D $$):

$$ I_D =I_S \ vezes e ^ \ frac {V_D} {0,026} $$

(Consulte a página sobre diodos e retificadores para obter mais informações sobre a equação corrente-tensão do diodo; também, observe que $$ I_S $$ é uma constante, não uma variável.) Para encontrar a taxa de variação da corrente em relação à tensão, tomamos a derivada:

$$ \ frac {\ text {d} I_D} {\ text {d} V_D} =\ frac {\ text {d}} {\ text {d} V_D} (I_S \ vezes e ^ \ frac {V_D} { 0,026}) =I_S \ vezes e ^ \ frac {V_D} {0,026} \ vezes \ frac {1} {0,026} $$

Assim, a um determinado valor de tensão do diodo $$ V_D $$, um aumento incremental na tensão criará um aumento na corrente igual a $$ \ frac {I_S} {0,026} e ^ \ frac {V_D} {0,026} $$ .



PLANILHAS RELACIONADAS:

• 
  Planilha de cálculo para circuitos elétricos