Técnicas de análise para circuitos de resistores paralelos em série

Diretrizes para Análise de Circuito de Combinação Série-Paralela

O objetivo da análise do circuito do resistor em série-paralelo é determinar todas as quedas de tensão, correntes e dissipações de potência em um circuito. A estratégia geral para atingir esse objetivo é a seguinte:

• Etapa 1: Avalie quais resistores em um circuito estão conectados em série simples ou em paralelo simples.
• Etapa 2: Desenhe novamente o circuito, substituindo cada uma das combinações de resistores em série ou paralelo identificadas na etapa 1 por um único resistor de valor equivalente. Se estiver usando uma tabela para gerenciar variáveis, faça uma nova coluna da tabela para cada equivalente de resistência.
• Etapa 3: Repita as etapas 1 e 2 até que todo o circuito seja reduzido a um resistor equivalente.
• Etapa 4: Calcule a corrente total a partir da tensão total e da resistência total (I =E / R).
• Etapa 5: Tomando os valores de tensão total e corrente total, volte para a última etapa no processo de redução do circuito e insira esses valores onde aplicável.
• Etapa 6: A partir das resistências conhecidas e dos valores de tensão total / corrente total da etapa 5, use a Lei de Ohm para calcular os valores desconhecidos (tensão ou corrente) (E =IR ou I =E / R).
• Etapa 7: Repita as etapas 5 e 6 até que todos os valores de tensão e corrente sejam conhecidos na configuração original do circuito. Essencialmente, você procederá passo a passo da versão simplificada do circuito de volta à sua forma original e complexa, conectando valores de tensão e corrente onde apropriado até que todos os valores de tensão e corrente sejam conhecidos.
• Etapa 8: Calcule as dissipações de potência a partir de valores conhecidos de tensão, corrente e / ou resistência.

Exemplo de análise de circuito de combinação série-paralelo

Isso pode parecer um processo intimidante, mas é muito mais fácil de entender por meio de exemplos do que por meio de descrições.

Calculando resistências paralelas

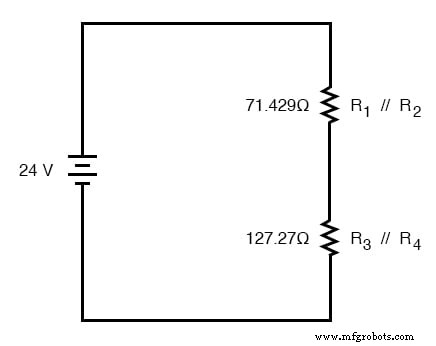
No exemplo de circuito acima, R ₁ e R ₂ estão conectados em um arranjo paralelo simples, assim como R ₃ e R ₄ . Tendo sido identificadas, essas seções precisam ser convertidas em resistores únicos equivalentes e o circuito redesenhado:



Os símbolos de barra dupla (//) representam “paralelo” para mostrar que os valores do resistor equivalente foram calculados usando a fórmula 1 / (1 / R). O resistor de 71,429 Ω no topo do circuito é equivalente a R ₁ e R ₂ em paralelo um com o outro. O resistor 127,27 Ω na parte inferior é o equivalente a R ₃ e R ₄ em paralelo um com o outro.

Nossa tabela pode ser expandida para incluir esses equivalentes de resistor em suas próprias colunas:



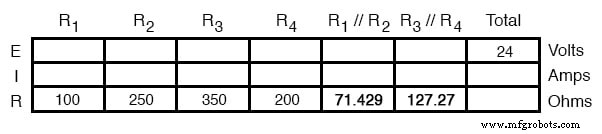
Deve ficar claro agora que o circuito foi reduzido a uma configuração em série simples com apenas duas resistências (equivalentes). A etapa final da redução é adicionar essas duas resistências para chegar a uma resistência total do circuito. Quando adicionamos essas duas resistências equivalentes, obtemos uma resistência de 198,70 Ω.

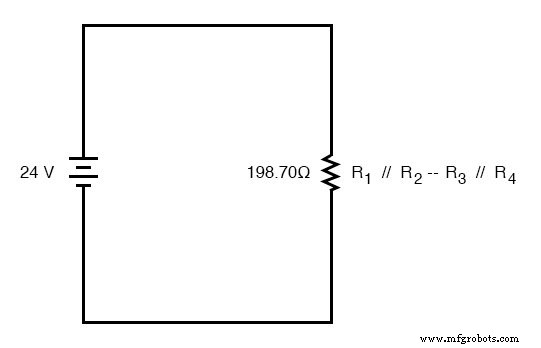
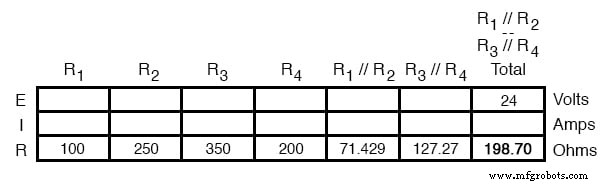
Agora, podemos redesenhar o circuito como uma única resistência equivalente e adicionar o valor da resistência total à coluna mais à direita de nossa tabela. Observe que a coluna “Total” foi renomeada (R ₁ // R ₂ —R ₃ // R ₄ ) para indicar como se relaciona eletricamente com as outras colunas de figuras. O símbolo “-” é usado aqui para representar “série”, assim como o símbolo “//” é usado para representar “paralelo”.

Cálculo de corrente e tensões

Agora, a corrente total do circuito pode ser determinada aplicando a Lei de Ohm (I =E / R) à coluna "Total" na tabela:



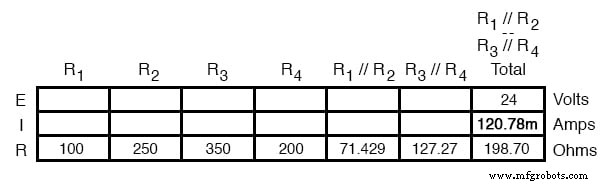
De volta ao nosso desenho de circuito equivalente, nosso valor de corrente total de 120,78 miliamperes é mostrado como a única corrente aqui:



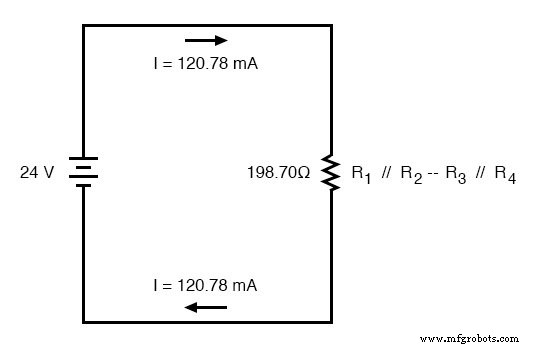
Agora começamos a retroceder em nossa progressão de redesenhos de circuitos para a configuração original. A próxima etapa é ir para o circuito onde R ₁ // R ₂ e R ₃ // R ₄ estão em série:



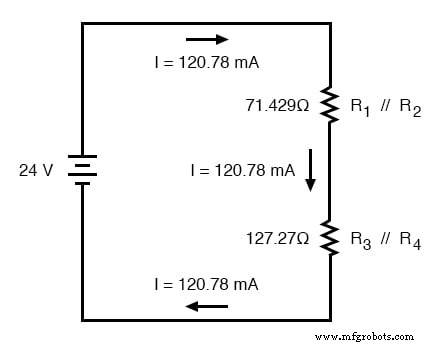
Desde R ₁ // R ₂ e R ₃ // R ₄ estão em série, a corrente através desses dois conjuntos de resistências equivalentes deve ser a mesma. Além disso, a corrente através deles deve ser igual à corrente total, para que possamos preencher nossa tabela com os valores de corrente apropriados, simplesmente copiando o valor atual da coluna Total para R ₁ // R ₂ e R ₃ // R ₄ colunas:



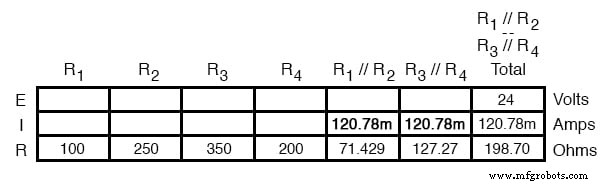
Agora, conhecendo a corrente através dos resistores equivalentes R ₁ // R ₂ e R ₃ // R ₄ , podemos aplicar a Lei de Ohm (E =IR) às duas colunas verticais direitas para encontrar quedas de tensão entre elas:





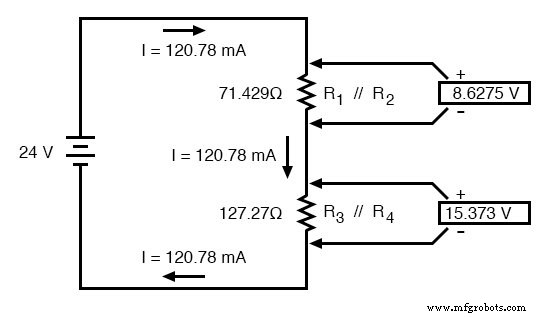
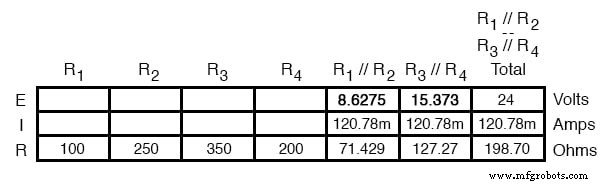
Porque sabemos R ₁ // R ₂ e R ₃ // R ₄ são equivalentes de resistores paralelos, e sabemos que as quedas de tensão em circuitos paralelos são iguais, podemos transferir as respectivas quedas de tensão para as colunas apropriadas na tabela para esses resistores individuais. Em outras palavras, damos outro passo para trás em nossa sequência de desenho para a configuração original e completamos a tabela de acordo:





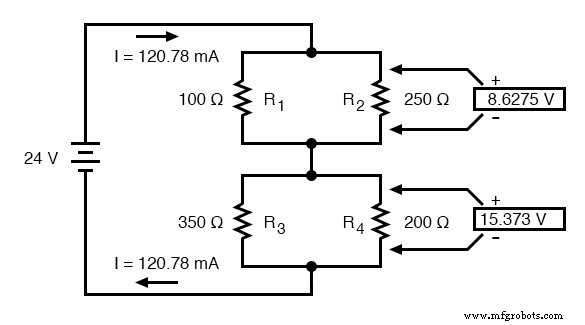
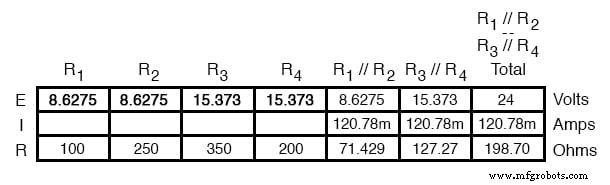
Finalmente, a seção original da tabela (colunas R ₁ até R ₄ ) está completo com valores suficientes para terminar. Aplicando a Lei de Ohm às colunas verticais restantes (I =E / R), podemos determinar as correntes através de R ₁ , R ₂ , R ₃ e R ₄ individualmente:

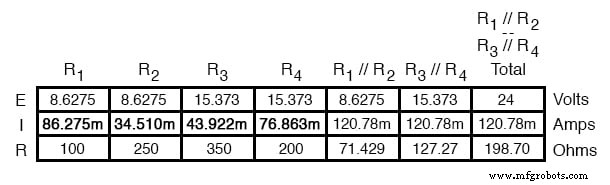
Colocando valores de tensão e corrente em diagramas

Tendo encontrado todos os valores de tensão e corrente para este circuito, podemos mostrar esses valores no diagrama esquemático como:



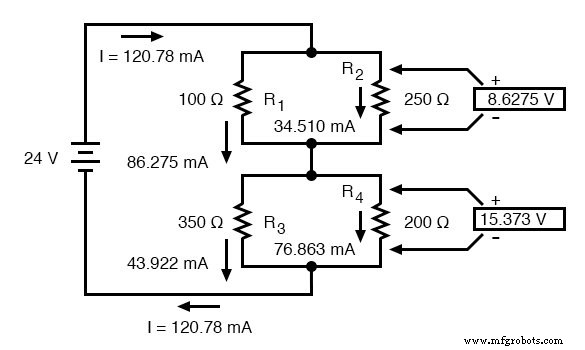
Como uma verificação final do nosso trabalho, podemos ver se os valores atuais calculados se somam como deveriam com o total. Desde R ₁ e R ₂ estão em paralelo, suas correntes combinadas devem somar o total de 120,78 mA. Da mesma forma, desde R ₃ e R ₄ estão em paralelo, suas correntes combinadas também devem somar o total de 120,78 mA. Você pode verificar por si mesmo se esses números somam conforme o esperado.

Usando SPICE para verificar valores calculados

Uma simulação de computador também pode ser usada para verificar a precisão dessas figuras. A seguinte análise do SPICE mostrará todas as tensões e correntes do resistor (observe as fontes de tensão "fictícias" de detecção de corrente vi1, vi2,.... ) Essas fontes de tensão serão configuradas para ter valores de zero volts cada, de forma que não afetarão o circuito de forma alguma.

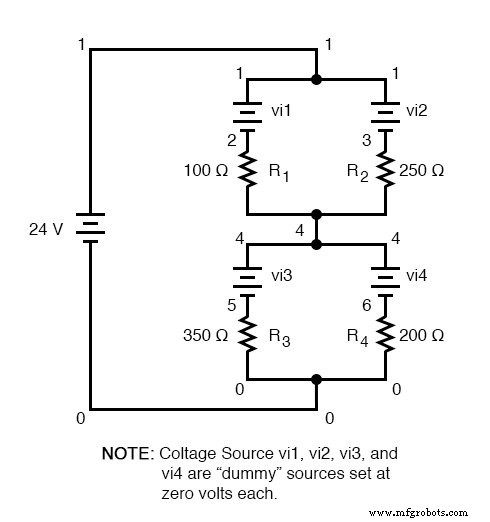
 circuito série-paralelo v1 1 0 vi1 1 2 dc 0 vi2 1 3 dc 0 r1 2 4 100 r2 3 4 250 vi3 4 5 dc 0 vi4 4 6 dc 0 r3 5 0 350 r4 6 0 200 .dc v1 24 24 1 .print DC v (2,4) v (3,4) v (5,0) v (6,0) .print dc i (vi1) i (vi2) i (vi3) i (vi4) .fim 

Anotei os valores de saída do SPICE para torná-los mais legíveis, denotando quais valores de tensão e corrente pertencem a quais resistores.
v1 v (2,4) v (3,4) v (5) v (6) 2,40E + 018,63E + 008,63E + 001,54E + 011,54E + 01Tensão da bateria R1 voltagem R2 voltagem R3 voltagem R4 voltagem v1 i (vi1) i (vi2) i (vi3) i (vi4) 2.40E + 018.63E-023.54EE-024.39E-027.69E-02Tensão da bateria R1 corrente R2 corrente R3 corrente R4
Como você pode ver, todos os números estão de acordo com os valores calculados.

REVER:

• Para analisar um circuito de combinação série-paralelo, siga estas etapas:
• Reduza o circuito original a um único resistor equivalente, redesenhando o circuito em cada etapa de redução, pois séries simples e partes paralelas simples são reduzidas a resistores equivalentes únicos.
• Resolva para resistência total.
• Resolva para a corrente total (I =E / R).
• Determine quedas de tensão de resistor equivalentes e correntes de ramificação um estágio de cada vez, voltando à configuração original do circuito novamente.

PLANILHAS RELACIONADAS:

• Planilha de manipulação de equações algébricas para circuitos elétricos
• Planilha de circuitos CC paralelos em série