Fator Q e largura de banda de um circuito ressonante

O fator Q, ou qualidade, de um circuito ressonante é uma medida da “bondade” ou qualidade de um circuito ressonante. Um valor mais alto para esta figura de mérito corresponde a uma largura de banda mais estreita, o que é desejável em muitas aplicações. Mais formalmente, Q é a relação entre a potência armazenada e a potência dissipada na reatância e resistência do circuito, respectivamente:

 Q =P  armazenado  / P  dissipado  =I 
 2 
 X / I 
 2 
 R Q =X / R onde:X =Reatância capacitiva ou indutiva na ressonância R =resistência em série. 

Esta fórmula é aplicável a circuitos ressonantes em série e também a circuitos ressonantes paralelos se a resistência estiver em série com o indutor. Este é o caso em aplicações práticas, já que estamos principalmente preocupados com a resistência do indutor que limita o Q.

Nota: Alguns textos podem mostrar X e R trocados na fórmula “Q” para um circuito ressonante paralelo. Isso está correto para um grande valor de R em paralelo com C e L. Nossa fórmula está correta para um pequeno R em série com L.

Uma aplicação prática de “Q” é que a tensão em L ou C em um circuito ressonante em série é Q vezes a tensão total aplicada. Em um circuito ressonante paralelo, a corrente através de L ou C é Q vezes a corrente total aplicada.

Circuitos ressonantes em série

Um circuito ressonante em série parece uma resistência na frequência de ressonância. Uma vez que a definição de ressonância é X _L =X _C , os componentes reativos se cancelam, deixando apenas a resistência contribuir para a impedância.

A impedância também é mínima na ressonância. Abaixo da frequência ressonante, o circuito ressonante em série parece capacitivo, uma vez que a impedância do capacitor aumenta para um valor maior do que a reatância indutiva decrescente, deixando um valor capacitivo líquido.

Acima da ressonância, a reatância indutiva aumenta, a reatância capacitiva diminui, deixando um componente indutivo líquido.







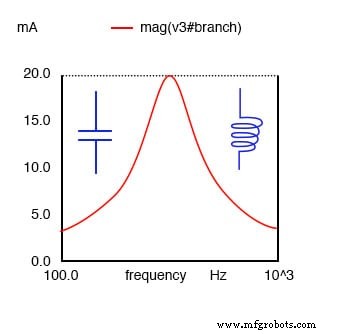
NOTA:

Na ressonância, o circuito ressonante em série parece puramente resistivo. Abaixo da ressonância, parece capacitivo. Acima da ressonância, parece indutivo. A corrente é máxima na ressonância e a impedância no mínimo. A corrente é definida pelo valor da resistência. Acima ou abaixo da ressonância, a impedância aumenta.

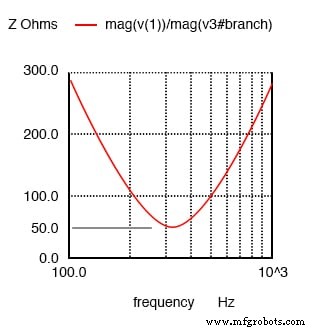
A impedância é mínima na ressonância em um circuito ressonante em série.

O pico da corrente ressonante pode ser alterado variando o resistor em série, que altera o Q. Isso também afeta a amplitude da curva. Um circuito de baixa resistência e Q alto tem uma largura de banda estreita, em comparação com um circuito de alta resistência e baixo Q.

Largura de banda em termos de Q e frequência ressonante:

 BW =f  c  / Q Onde f  c  =frequência ressonante Q =fator de qualidade 

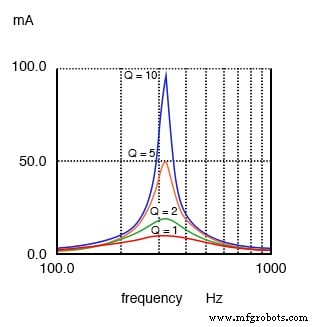
Um circuito ressonante Q alto tem uma largura de banda estreita em comparação com um Q baixo

A largura de banda é medida entre os pontos de amplitude de corrente de 0,707. Os 0,707 pontos de corrente correspondem à metade dos pontos de potência, pois P =I ² R, (0,707) ² =(0,5).

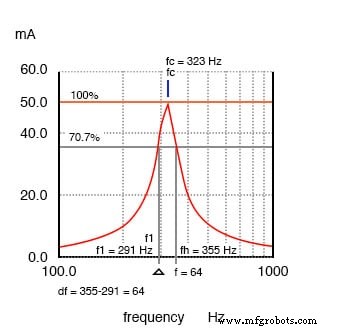
Largura de banda, Δf é medido entre os pontos de amplitude de 70,7% do circuito ressonante em série.

 BW =Δf =f  h  -f  l  =f  c  / Q Onde:f  h  =borda de banda alta f  l  =borda de banda baixa f  l  =f  c  - Δf / 2 f  h  =f  c  + Δf / 2 Onde f  c  =frequência central (frequência ressonante) 

Na Figura acima, o ponto de corrente de 100% é 50 mA. O nível de 70,7% é 0,707 (50 mA) =35,4 mA. As bordas da banda superior e inferior lidas da curva são 291 Hz para fl e 355 Hz para f _h . A largura de banda é de 64 Hz, e os pontos de meia potência são ± 32 Hz da frequência ressonante central:

 BW =Δf =f  h  -f  l  =355-291 =64 f  l  =f  c  - Δf / 2 =323-32 =291 f  h  =f  c  + Δf / 2 =323 + 32 =355 

Uma vez que BW =fc / Q:

Q =f _c / BW =(323 Hz) / (64 Hz) =5

Circuitos Ressonantes Paralelos

A impedância de um circuito ressonante paralelo é máxima na frequência ressonante. Abaixo da frequência ressonante, o circuito ressonante paralelo parece indutivo, uma vez que a impedância do indutor é menor, consumindo a maior proporção da corrente.

Acima da ressonância, a reatância capacitiva diminui, extraindo a maior corrente, assumindo assim uma característica capacitiva.

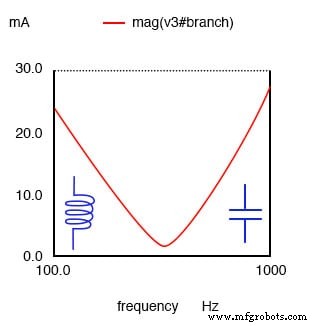
Um circuito ressonante paralelo é resistivo na ressonância, indutivo abaixo da ressonância e capacitivo acima da ressonância.

A impedância é máxima na ressonância em um circuito ressonante paralelo, mas diminui acima ou abaixo da ressonância. A tensão está em um pico na ressonância, pois a tensão é proporcional à impedância (E =IZ).

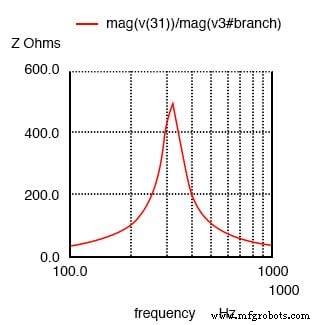
Circuito ressonante paralelo:pico de impedância na ressonância.



Um Q baixo devido a uma alta resistência em série com o indutor produz um pico baixo em uma ampla curva de resposta para um circuito ressonante paralelo. Um Q alto é devido a uma baixa resistência em série com o indutor. Isso produz um pico mais alto na curva de resposta mais estreita. O Q alto é obtido enrolando o indutor com maior diâmetro (bitola menor), fio de menor resistência.

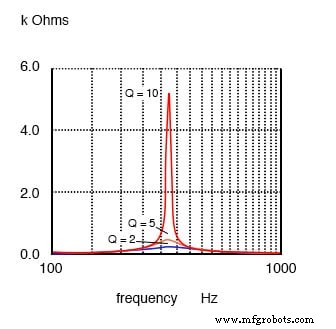
A resposta ressonante paralela varia com Q.



A largura de banda da curva de resposta ressonante paralela é medida entre os pontos de meia potência. Isso corresponde aos pontos de tensão de 70,7%, uma vez que a potência é proporcional a E ² . ((0,707) ² =0,50) Como a tensão é proporcional à impedância, podemos usar a curva de impedância.

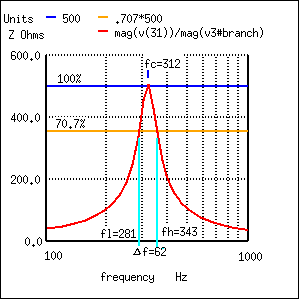
Largura de banda, Δf é medido entre os pontos de impedância de 70,7% de um circuito ressonante paralelo.



Na figura acima, o ponto de impedância de 100% é 500 Ω. O nível de 70,7% é 0707 (500) =354 Ω. As bordas da banda superior e inferior lidas da curva são 281 Hz para fl e 343 Hz para fh. A largura de banda é de 62 Hz, e os pontos de meia potência são ± 31 Hz da frequência ressonante central:

 BW =Δf =f  h  -f  l  =343-281 =62 f  l  =f  c  - Δf / 2 =312-31 =281 f  h  =f  c  + Δf / 2 =312 + 31 =343 

 Q =fc / BW =(312 Hz) / (62 Hz) =5 

PLANILHAS RELACIONADAS:

• Planilha de ressonância
• Substituição algébrica para planilha de circuitos elétricos