Teorema da Superposição - Análise de Circuito com Exemplo Resolvido
Teorema da Superposição – Guia Passo a Passo com Exemplo Resolvido
O que é o Teorema da Superposição?
O Teorema da Superposição é usado para resolver redes complexas com várias fontes de energia. É um conceito importante determinar a tensão e a corrente através dos elementos calculando o efeito de cada fonte individualmente. E combine o efeito de todas as fontes para obter a tensão e a corrente reais do elemento do circuito.
O teorema da superposição afirma que;
Em outras palavras, consideraremos apenas uma fonte independente atuando por vez. Então, precisamos remover outras fontes. As fontes de tensão estão em curto-circuito e as fontes de corrente estão em circuito aberto para fontes ideais. Se a resistência interna das fontes for fornecida, você precisará considerar o circuito.
O teorema da superposição só é aplicado ao circuito que segue a lei de Ohm.
- Post relacionado: Teorema de Thevenin. Guia passo a passo com exemplo resolvido
Quando usar o Teorema da Superposição?
A rede deve seguir os requisitos abaixo para aplicar o teorema da superposição.
- Os componentes usados no circuito devem ser lineares. Isso significa que, para resistores, o fluxo de corrente é proporcional à tensão; para indutores, a ligação de fluxo é proporcional à corrente. Portanto, o resistor, o indutor e o capacitor são elementos lineares. Mas o diodo, transistor não é um elemento linear.
- Os componentes do circuito devem ser elementos bilaterais. Isso significa que a magnitude da corrente é independente da polaridade das fontes de energia.
- Com a ajuda do teorema da superposição, podemos encontrar a corrente que passa por um elemento, a queda de tensão da resistência e a tensão do nó. Mas não podemos encontrar a potência dissipada do elemento.
- Post relacionado: Teorema de Norton. Guia passo a passo com exemplo resolvido
Passos a seguir para o Teorema da Superposição
Etapa 1 Descubra uma série de fontes independentes disponíveis na rede.
Etapa 2 Escolha qualquer fonte e elimine todas as outras fontes. Se a rede consistir em qualquer fonte dependente, você não poderá eliminá-la. Permanece como está durante todo o cálculo.
Se você considerou todas as fontes de energia como fontes ideais, não precisa considerar a resistência interna. E diretamente fonte de tensão de curto-circuito e fonte de corrente de circuito aberto. Mas no caso, se for fornecida resistência interna das fontes, você deve substituir a resistência interna.
Etapa 3 Agora, em um circuito, apenas uma fonte de energia independente está presente. Você precisa encontrar uma resposta com apenas uma fonte de energia no circuito.
Etapa 4 Repita os passos 2 e 3 para todas as fontes de energia disponíveis na rede. Se houver três fontes independentes, você precisará repetir essas etapas três vezes. E toda vez você obtém algum valor da resposta.
Etapa-5 Agora, combine todas as respostas por soma algébrica obtidas por fontes individuais. E você obterá um valor final de resposta para um elemento específico de uma rede. Se você precisar encontrar uma resposta para outros elementos, precisará seguir estas etapas novamente para esse elemento.
- Post relacionado: Análise de circuito SUPERMESH – passo a passo com exemplo resolvido
Exemplo resolvido do teorema da superposição
Exemplo:
Vamos entender o funcionamento do teorema da superposição por exemplo. Encontre a corrente (IL ) passa pelo resistor de 8Ω na rede dada usando o teorema da superposição.
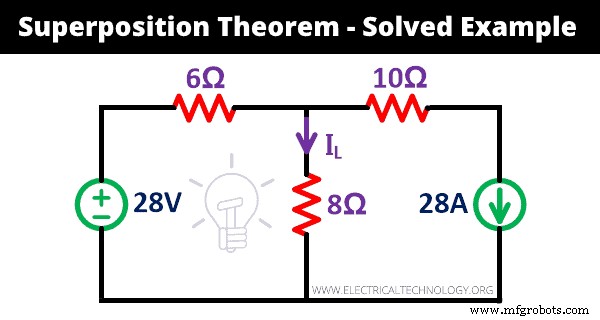
Solução:
Etapa 1 Como mostrado na rede acima, uma fonte de tensão e uma fonte de corrente são fornecidas. Portanto, precisamos repetir o procedimento duas vezes.
Etapa 2 Primeiro, consideramos que a fonte de tensão de 28V está presente na rede. Portanto, você precisa remover a fonte de corrente por terminais em circuito aberto. Como aqui, consideramos a fonte de corrente como uma fonte de corrente ideal. Portanto, não precisamos conectar a resistência interna.
O circuito restante é mostrado na figura abaixo.
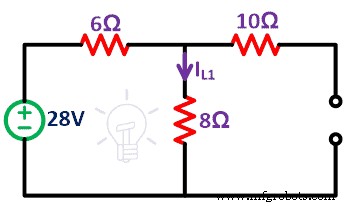
Etapa 3 Encontre a corrente (IL1 ) passa pelo resistor de 8Ω. Dá o efeito apenas de uma fonte de tensão.
Devido ao circuito aberto de uma fonte de corrente, nenhuma corrente passa pelo resistor de 10Ω. Assim, a rede consiste em apenas um loop.
Aplicar KVL ao loop;
28 =6Eu L 1 + 8Eu L 1
28 =14Eu L 1
Eu L 1 =28/14
Eu L 1 =2A
Etapa 4 Agora, repetimos o mesmo procedimento para a fonte atual. Nesta condição, removemos a fonte de tensão por curto-circuito. Um circuito restante é como mostrado na figura abaixo.
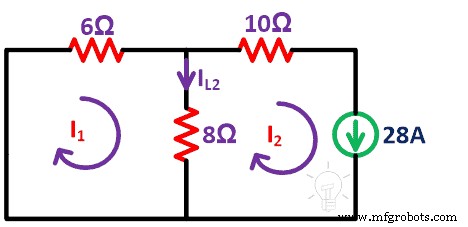
Aqui, temos que considerar dois loops. Eu1 e eu2 são correntes de loop. E encontre o IL2 atual .
Aplica KVL ao loop-1;
0 =6I 1 + 8Eu 1 – 8Eu 2
14Eu 1 – 8Eu 2 =0
A corrente que passa pelo loop-2 é calculada a partir da fonte atual. E será;
Eu 2 =28A
Coloque este valor na equação acima;
14Eu 1 – 8 (28) =0
Eu 1 =16A
Agora, a ramificação do resistor de 8Ω é comum em ambos os loops. Então, precisamos encontrar a corrente resultante (IL2 ) passa pelo resistor de 8Ω.
Eu L 2 =Eu 1 – Eu 2
Eu L 2 =16 – 28
Eu L 2 =-12A
Etapa-5 Agora, combinamos o efeito de ambas as fontes pela soma algébrica da corrente. Então, a corrente total que passa pelo resistor de 8Ω é IL . Aqui, a direção da corrente é mais importante. Atual IL2 tem um sinal de menos. Isso significa que durante a fonte de 28A, a corrente flui na direção oposta. E não podemos mudar a direção. Essa é a razão pela qual ao combinar todas as fontes, estamos fazendo a soma algébrica.
Eu L =EuE 1 – EuE 2
Eu L =2 + (-12)
Eu L =-10A
Aqui, assumimos que a corrente que passa pelo resistor de 8Ω está na direção da seta mostrada na figura. O sinal de menos mostra a direção oposta. E a quantidade de corrente é 8A.
- Post relacionado:Análise de circuito SUPERNODE - passo a passo com exemplo resolvido
Experiência do Teorema da Superposição
O experimento do teorema da superposição pode ser feito seguindo as etapas abaixo.
Mirar
Determine a corrente que flui através dos resistores e verifique o teorema da superposição.
Componentes obrigatórios
Fonte CC, resistores, multímetros CC, fios de conexão, placa de ensaio, etc.
Teoria
O teorema da superposição é usado na análise de circuitos para encontrar a corrente e a tensão entre os elementos de um determinado circuito. Este teorema é útil quando o número de fontes é maior.
De acordo com o teorema da superposição, a resposta dos elementos é uma soma algébrica da resposta das fontes de energia individuais.
Primeiro, vamos calcular a corrente que passa pelos resistores em uma determinada rede. Quando todas as fontes estão conectadas. Depois disso, removemos fontes e encontramos correntes para fontes individuais. Por fim, a soma da corrente medida das fontes individuais é semelhante às medidas de corrente com todas as fontes conectadas.
Procedimento
Consideramos o circuito bilateral linear dado na figura abaixo.
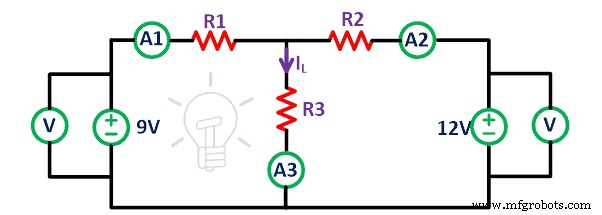
Conecte todos os elementos na placa de ensaio conforme indicado no circuito acima usando fios de conexão. Conecte o amperímetro com todos os resistores para encontrar a corrente que passa pelos resistores. Aqui, temos duas fontes de tensão.
No primeiro caso, meça a corrente que passa por todos os resistores quando ambas as fontes de tensão estão presentes no circuito. A corrente que flui através do resistor R1 , R2 e R3 é eu 1 , Eu 2 , e eu 3 respectivamente.
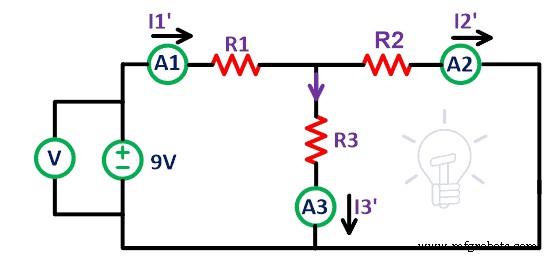
Agora remova a fonte de tensão de 12V do circuito. Curto-circuite os terminais A' e B' conforme mostrado na figura acima. Aqui assumimos que as fontes de tensão são ideais. Portanto, não há necessidade de conectar resistência interna. Agora, meça o atual I 1′ , Eu 2′ e eu 3′ que é a corrente que passa pelo resistor R1, R2 e R3, respectivamente.
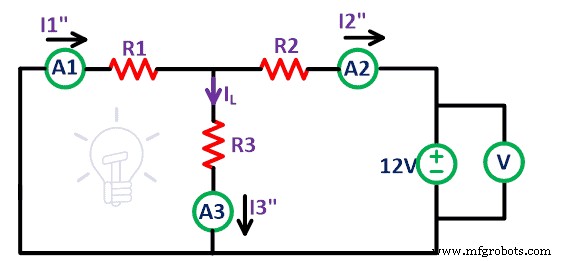
Da mesma forma, remova a fonte de tensão de 9V e o circuito restante é mostrado na figura acima. Novamente, meça a corrente que flui através de todos os resistores e nomeie-a I 1 “ , Eu 2 “ , e eu 3 “ .
- Post relacionado: Teorema de Transferência de Potência Máxima para Circuitos CA e CC
Coloque todos os valores na tabela de observação abaixo.
Tabela de Observação
| Conexão de origem | R1 | R2 | R3 |
| Ambas as fontes estão conectadas | Eu 1 | Eu 2 | Eu 3 |
| Apenas 12V está conectado | Eu 1′ | Eu 2′ | Eu 3′ |
| Apenas 9V está conectado | Eu 1″ | Eu 2″ | Eu 3″ |
Cálculo :
Eu 1 =Eu 1′ + Eu 1″
Eu 2 =Eu 2′ + Eu 2″
Eu 3 =Eu 3′ + Eu 3″
Para verificar o teorema da superposição, comparamos a soma algébrica da corrente que passa por resistores quando uma fonte individual é conectada com a corrente medida quando ambas as fontes estão conectadas em um circuito.
Se o cálculo acima for satisfatório, podemos provar o teorema da superposição.
Conclusão
Neste experimento, podemos provar que a corrente que passa pela resistência é uma soma algébrica da corrente quando uma fonte de energia individual é conectada. E prova o teorema da superposição.
- Post relacionado:Lei da Corrente e Tensão de Kirchhoff (KCL &KVL) | Exemplo resolvido
Aplicação do teorema da superposição
- O teorema da superposição pode ser usado para redes CA e CC.
- Quando o número de fontes independentes é maior, é fácil encontrar uma resposta da rede.
- Ajuda a calcular as passagens de corrente e a tensão através do elemento calculando o efeito de cada fonte de energia individualmente. E depois podemos determinar o efeito combinado em elementos de todas as fontes.
Desvantagem do Teorema da Superposição
- O teorema da superposição não pode ser aplicado ao circuito tendo apenas uma fonte dependente. Ele precisava de pelo menos duas fontes independentes.
- Este teorema só se aplica à rede que consiste em elementos lineares. Não pode ser aplicado a elementos não lineares como diodo, transistor, etc.
- Não podemos calcular a potência por este teorema. Como a potência é proporcional ao quadrado da tensão e da corrente, ela se torna não linear.
- Este teorema não é aplicável em uma condição em que a resistência varia com a tensão e a corrente. Para todas as fontes de energia, o valor da resistência deve permanecer constante.
- Este teorema só se aplica aos elementos bilaterais. Se a resposta da rede depende da direção da corrente, este teorema não é aplicável.
Tutoriais de análise de circuitos elétricos relacionados:
- Teorema de Tellegen - Exemplos Resolvidos e Simulação MATLAB
- Calculadora de Regras de Cramer - Sistema de 2 e 3 Equações para Circuitos Elétricos
- Ponte de Wheatstone – Circuito, Funcionamento, Derivação e Aplicações
- Calculadoras de engenharia elétrica e eletrônica
- Mais de 5.000 fórmulas e equações de engenharia elétrica e eletrônica
Tecnologia industrial
- Circuito com interruptor
- Opções de análise
- Exemplo de circuitos e listas de rede
- Análise de falha de componente
- O que é análise de rede?
- Estrutura C++ com exemplo
- std::list em C++ com exemplo
- Contador Python em coleções com exemplo
- Teorema de Tellegen – Exemplos resolvidos e simulação MATLAB
- O que fazer com placas de circuito antigas



