Teorema de Tellegen – Exemplos resolvidos e simulação MATLAB

Teorema de Tellegen – Guia passo a passo com exemplos resolvidos

O que é o Teorema de Tellegen?

Teorema de Tellegen foi publicado por um engenheiro elétrico e inventor holandês Bernard D.H. Tellegen em 1952. Este teorema é o teorema mais importante e fundamental entre outros teoremas na análise de redes. A maioria dos outros teoremas são derivados deste teorema.

O teorema de Tellegen depende da lei de Kirchhoff. Portanto, este teorema pode ser aplicado à rede que obedece à lei de Kirchhoff. Este teorema pode ser aplicado a uma ampla faixa da rede com elementos lineares ou não lineares, variantes ou não variantes no tempo, passivos ou ativos.

O teorema de Tellegen afirma que;

O teorema de Tellegen funciona com base no princípio da lei da conservação da energia. Este teorema é usado em aplicações químicas e biológicas para encontrar o comportamento dinâmico da rede física. No processamento de sinais, este teorema é usado para projetar filtros.

• Post relacionado:Teorema de Thévenin. Guia passo a passo com exemplo resolvido

Equação matemática

Para uma análise geral do teorema, consideramos que o número ‘n’ de elementos é dado na rede. A corrente instantânea que passa pelo elemento é i₁ , i₂ , i₃ , …., i_n . E a tensão instantânea deste ramo é v₁ , v₂ , v₃ , …., v_n .

Portanto, a corrente instantânea e a tensão do elemento-1 são i₁ e v₁ . A potência instantânea (p₁ ) consumido por este elemento é v₁ e₁ .

p ₁ =v ₁ eu ₁

O poder instantâneo do elemento-2 é (p ₂ );

p ₂ =v ₂ eu ₂

Da mesma forma, o poder instantâneo de n ^th elemento é (p _n );

p_n =v_n e_n

De acordo com o teorema de Tellegen, a soma de todas as potências instantâneas é zero. Isso significa que precisamos somar todas as potências instantâneas p₁ , p₂ , p₃ , …., p_n .

p ₁ + p ₂ + p ₃ + … + p_n = 0

v ₁ eu ₁ + v ₂ eu ₂ + v ₃ eu ₃ + … + v_n e_n  = 0

De forma geral, podemos escrever a equação acima para o k ^th ramo;

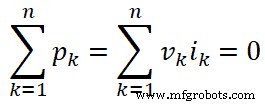
Onde,

• n =número total de filiais na rede
• v_k =tensão instantânea de k ^th filial
• i_k =corrente instantânea de k ^th filial
• p_k =potência instantânea de k ^th filial

Agora, considere a figura abaixo, pois o ramo AB é igual ao ramo k.

Portanto, tensão instantânea v_k ;

v_k =v_a – v_b

E a corrente instantânea que passa pelo ramo (a a b) é i_k ;

i_k =i_ab

Então, a potência instantânea p_k é;

p_k =v_k eu_k =(v_um – v_b ) i_ab ….. (1)

Agora, consideramos o sentido oposto da corrente instantânea (b para a);

i_ab =– i_ab

Tensão instantânea;

v_k =v_b – v_a

A potência instantânea p_k é;

p_k =v_k eu_k =(v_b – v_a ) eu_ba ….. (2)

Soma da equação-1 e 2;

2v_k eu_k =(v_a – v _b )eu _ab + (v_b – v_a ) i_ba

v_k eu_k =1/2 [(v_a – v _b )eu _ab + (v_b – v_a ) e_ba ] ….. (3)

Esta equação pode ser escrita como abaixo para n-ramificações;

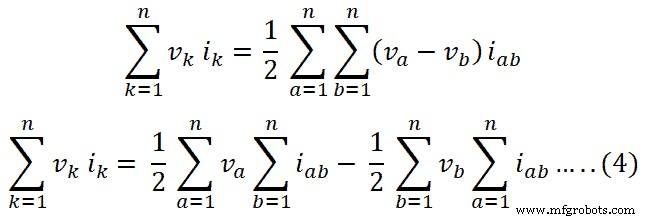
De acordo com a lei das correntes de Kirchhoff, a soma algébrica da corrente é zero em um nó do circuito.

Portanto,

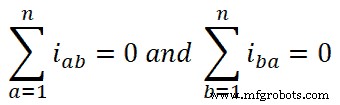
Se colocarmos esse valor na equação-4, obtemos;

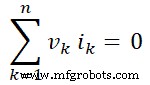
Assim, fica provado que a soma da potência entregue à rede é zero. Portanto, está provado o teorema de Tellegen. Também é descrito que a soma das potências absorvidas pelos elementos da rede é igual à soma das potências entregues pelas fontes.

• Post relacionado: Teorema de Norton. Guia passo a passo com exemplo resolvido

Passos a seguir para o Teorema de Tellegen

Precisamos seguir os passos abaixo para resolver qualquer rede elétrica pelo teorema de Tellegen.

Etapa 1: Precisamos encontrar um número de ramificações na rede elétrica fornecida. Em seguida, encontre a potência dissipada em cada ramo. Para encontrar a potência, precisamos encontrar a tensão ou corrente desse ramo usando qualquer método de análise convencional.

Etapa 2: Encontre a potência instantânea de cada ramo.

Etapa 3: O ramal que possui uma fonte de energia que é considerado um ramal de fornecimento de energia. E o ramo possui outros elementos é considerado como um ramo absorvedor de energia. Agora identifique a ramificação de fornecimento de energia e a ramificação de absorção de energia.

Etapa 4: Suponha sinal positivo no ramo de fornecimento de energia e queda de tensão negativa no ramo de absorção de energia. Você pode assumir sinais inversos também. Mas não pode mudar ao longo do exemplo.

Etapa-5: Para justificar o teorema de Tellegen, precisamos somar todas as potências calculadas de todos os ramos. E esta soma é sempre zero.

• Post relacionado: Análise de circuito SUPERMESH – passo a passo com exemplo resolvido

Vamos entender com um exemplo.

Exemplo resolvido do teorema de Tellegen

Exemplo nº 1

Justifique o teorema de Tellegen para a rede abaixo.

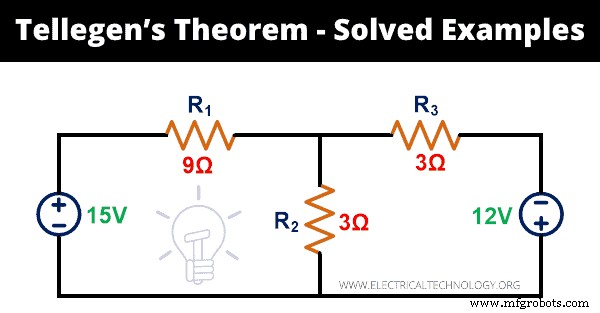
Solução:

Etapa 1: A rede de circuitos dada tem 5 ramos. Para calcular a potência instantânea, precisamos encontrar a corrente que passa por cada ramo. Para isso, aplicaremos o KVL à rede.

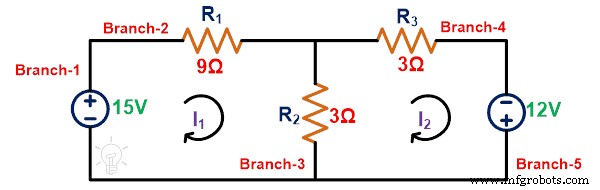
Aplica KVL ao loop-1;

15 =12Eu ₁ – 3Eu ₂

Aplica KVL ao loop-2;

12 =– 3Eu ₂ + 6Eu ₂

Resolvendo as equações acima, podemos encontrar os valores da corrente de loop I₁ e eu₂ . E esses valores são;

Eu ₁ =2A

Eu ₂ =3A

Etapa 2: A corrente que passa pelo ramo-3 é;

Eu _{1 2} =Eu ₂ – Eu ₁ =3 – 2 =1A

Temos corrente fluindo por todas as ramificações. Agora, encontre o poder de cada ramo.

P ₁ =V I ₁ =15 x 2 =30 W

P ₂ =R ₁ Eu ₁ ² =9 x 4 =36 W

P ₃ =R ₁ Eu ₁₂ ² =3 x 1 =3W

P ₄ =R ₃ Eu ₂ ² =3 x 9 =27 W

P ₅ =V I ₂ =12 x 3 =36 W

Etapa 3: Existem dois ramos com fontes. Esses ramos são ramos de fornecimento de energia e os outros três ramos são ramos de absorção de energia.

Aqui, para este exemplo, assumimos que o sinal do ramo de fornecimento de energia é positivo e o sinal do ramo de absorção de energia é negativo. Portanto, as ramificações 1 e 5 são ramificações de fornecimento de energia e outras ramificações são ramificações de absorção de energia.

Etapa 4: O sinal de poder P₁ e P₅ é positivo (ramificações de fornecimento de energia) e o sinal de P₂ , P₃ , e P₄ é negativo (ramos absorvedores de energia).

Etapa-5: Agora, precisamos encontrar a soma da potência dissipada por todos os ramos.

P ₁ – P ₂ – P ₃ – P ₄ + P ₅ =30W – 36W – 3W – 27W + 36W =0W

Então, a soma da potência instantânea é zero. E, portanto, este teorema está provado.

• Post relacionado:Análise de circuito SUPERNODE - passo a passo com exemplo resolvido

Exemplo nº 2

Encontre a tensão na fonte de corrente de 6A usando o teorema de Tellegen.

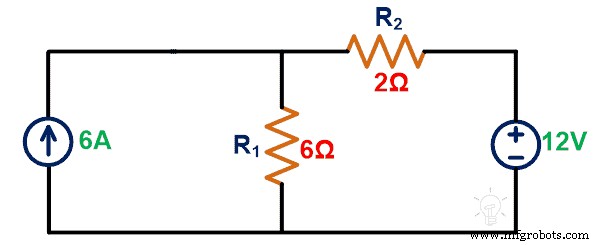
Solução:

Etapa 1: Precisamos calcular a tensão ou a corrente que passa pelo elemento. Para isso, aplicamos KCL ou KVL à rede fornecida.

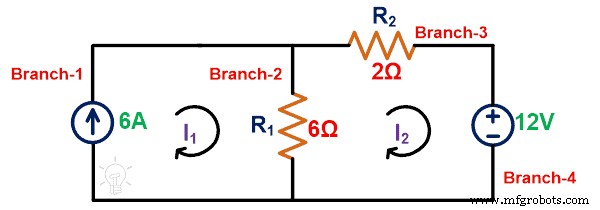
Aplica KVL ao loop-2;

-12 =8I ₂ – 6Eu ₁

As passagens atuais pela ramificação com a fonte atual são I ₁;

Eu ₁ =6A

Coloque este valor na equação acima;

-12 =8I ₂ – 6(6)

-12 =8I ₂ - 36

36 – 12 =8I ₂

24 =8Eu ₂

Eu ₂ =3A

Etapa 2: A corrente passa pelo branch-2 é;

Eu ₁₂ =Eu ₁ – Eu ₂ =6 – 3 =3A

Agora, encontre o poder de cada ramo;

P ₁ =V I ₁ =V x 6 =6 x V

P ₂ =R ₁ Eu ₁₂ ² =6 x 9 =54 W

P ₄ =R ₂ Eu ₂ ² =2 x 9 =18 W

P ₄ =V I ₂ =-12 x 3 =-36W

Etapa 3: Aqui, dois ramos com fontes de energia. Portanto, temos que considerar esses ramos como ramos de fornecimento de energia. E defina o sinal positivo para a potência instantânea.

Os outros dois ramos possuem apenas resistores. Portanto, esses ramos são ramos absorventes de energia e definem o sinal negativo para a potência instantânea.

Etapa 4: Potência P₁ e P₄ tem sinal positivo e potência P₂ e P3 têm sinal negativo.

Etapa-5: Agora, precisamos somar toda a potência instantânea.

P ₁ – P ₂ – P ₃ + P ₄ =0W

P ₁ – 54 – 18 + 36 =108 W

A potência fornecida pela fonte de corrente de 6A é de 108W. Portanto, a tensão na fonte de corrente é calculada por;

P ₁ =V I

108W =V x 6A

V =18V

Portanto, a tensão na fonte de corrente é 18V.

• Post relacionado: Teorema de Transferência de Potência Máxima para Circuitos CA e CC

Analisando e Simulando o Teorema de Tellegen usando MATLAB  

Objectivo:

Prove o Teorema de Tellegen para o diagrama de circuito dado no exemplo acima.

Requisito: MATLAB

Teoria:

De acordo com o teorema de Tellegen, a potência instantânea da soma de todos os ramos é igual a zero. Para provar este teorema, precisamos calcular a potência instantânea de todos os ramos.

Para encontrar a potência instantânea, precisamos calcular a tensão ou corrente de todos os ramos. Para isso, podemos usar os teoremas KCL ou KVL. Mas aqui vamos usar o modelo MATLAB Simulink para encontrar a corrente e a tensão.

Podemos usar outros softwares também como multisim, psim, etc. Construiremos um diagrama de circuito no modelo Simulink. Pelo modelo Simulink, você pode encontrar a tensão e a corrente de cada ramal.

Depois disso, você pode encontrar a potência instantânea da tensão e da corrente. Você pode encontrar diretamente a energia instantânea de algum software.

Modelo MATLAB Simulink

A figura abaixo mostra o diagrama de circuito do exemplo acima.

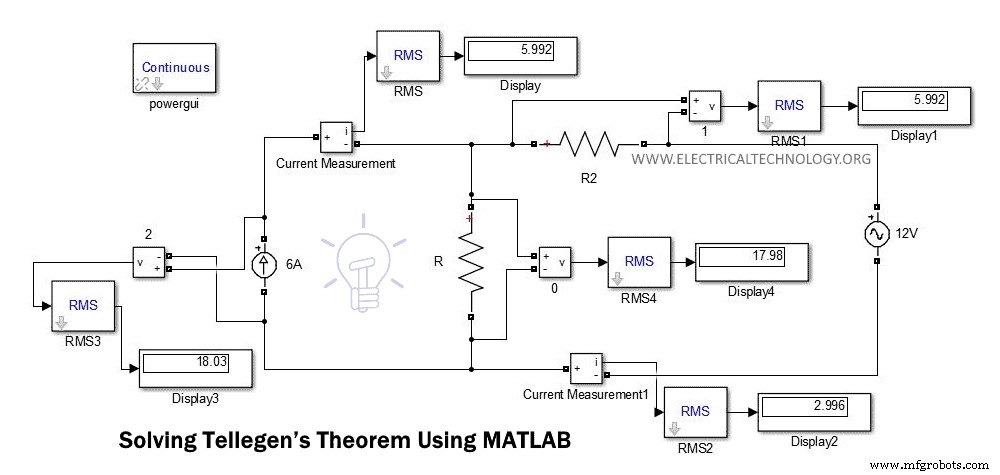
Nesta figura, podemos encontrar diretamente a tensão e a corrente do display. Você pode comparar esses valores calculando a tensão e a corrente com a ajuda de KCL ou KVL.

Cálculo

Após calcular a tensão ou corrente, você pode encontrar a potência instantânea. Ou você pode encontrar diretamente a energia instantânea do software. Tudo o que precisamos é de energia instantânea. E depois disso, precisamos adicionar todos os poderes.

A soma das potências é sempre zero. Para este exemplo, comparamos o valor de tensão e corrente encontrado no Simulink e os mesmos valores calculados no exemplo anterior usando KVL e KCL. Esses valores são os mesmos.

Esses valores também são calculados pelos resistores e fontes de conexão na placa de ensaio. E podemos medir a tensão e a corrente que passa por todos os ramos com a ajuda de um voltímetro e amperímetro.

Assim, fica provado o teorema de Tellegen.

• Post relacionado:Lei da Corrente e Tensão de Kirchhoff (KCL &KVL) | Exemplo resolvido

Aplicação do Teorema de Tellegen

Este teorema é muito fundamental e amplamente utilizado na análise de circuitos. Existem muitas aplicações deste teorema. Alguns aplicativos estão listados abaixo.

• Para projetar os filtros, este teorema é muito útil nas aplicações de processamento digital de sinais.
• Para determinar a estabilidade de plantas químicas, este teorema é usado em engenharia química.
• Este teorema se aplica ao sistema concentrado com elementos linear-não-linear, ativo-passivo, variante no tempo/invariante no tempo.
• Este teorema é usado no processo biológico.
• É usado em topologia e análise de reação de estrutura.
• Também é usado para encontrar o comportamento dinâmico da rede física.

• Teorema da Superposição - Análise de Circuito com Exemplo Resolvido
• Calculadora de Regras de Cramer - Sistema de 2 e 3 Equações para Circuitos Elétricos
• Ponte de Wheatstone – Circuito, Funcionamento, Derivação e Aplicações
• Calculadoras de engenharia elétrica e eletrônica
• Mais de 5.000 fórmulas e equações de engenharia elétrica e eletrônica