Práticas recomendadas de empilhamento de tolerância

O empilhamento de tolerância, também conhecido como empilhamento de tolerância, refere-se à combinação de várias tolerâncias de dimensão da peça. Depois que uma tolerância é identificada na dimensão de uma peça , é importante testar se essa tolerância funcionaria com as ferramentas tolerâncias:a extremidade superior ou a extremidade inferior. Uma peça ou montagem pode estar sujeita a imprecisões quando suas tolerâncias são empilhadas incorretamente.

A importância das tolerâncias

As tolerâncias influenciam diretamente o custo e o desempenho de um produto. Tolerâncias mais apertadas tornam uma peça usinada mais difícil de fabricar e, portanto, muitas vezes mais cara. Com isso em mente, é importante encontrar um equilíbrio entre a fabricação da peça, sua funcionalidade e seu custo.

Dicas para um empilhamento de tolerância bem-sucedido

Evite usar tolerâncias desnecessariamente pequenas

Como dito acima, tolerâncias mais apertadas levam a um custo de fabricação mais alto, pois a peça é mais difícil de fazer. Esse custo mais alto geralmente se deve ao aumento da quantidade de peças sucateadas que pode ocorrer quando as dimensões estão fora da tolerância. O custo de porta-ferramentas de alta qualidade e ferramentas com tolerâncias mais apertadas também podem ser uma despesa adicional.

Além disso, tolerâncias desnecessariamente pequenas levarão a tempos de fabricação mais longos, à medida que mais trabalho é necessário para garantir que a peça atenda a critérios rigorosos durante a usinagem e após a usinagem no processo de inspeção.

Tenha cuidado para não dimensionar demais uma peça

Quando uma tolerância superior e inferior é rotulada em cada recurso de uma peça, o superdimensionamento pode se tornar um problema. Por exemplo, uma fresa de topo com raio de canto com raios de canto direito e esquerdo pode ter uma tolerância de +/- 0,001”, e o plano entre eles tem uma tolerância de 0,002”. Neste caso, a janela de tolerância para o diâmetro da fresa seria +/- 0,004”, mas muitas vezes é mal calculada durante o dimensionamento da peça. Além disso, colocar uma tolerância nesta chamada faria com que ela fosse superdimensionada e, portanto, a dimensão de referência "REF" deve ser deixada para ocupar o lugar da tolerância.

Utilize a análise estatística de tolerância:

A análise estatística analisa a probabilidade de que todas as três tolerâncias estejam abaixo ou acima da largura da ranhura dimensionada, com base em um desvio padrão. Essa probabilidade é representada por uma função densidade de probabilidade normal, que pode ser vista na figura 2 abaixo. Ao combinar todas as probabilidades das diferentes peças e dimensões em um projeto, podemos determinar a probabilidade de que uma peça tenha um problema ou falhe completamente, com base nas dimensões e tolerância das peças. Geralmente este método de análise é usado apenas para montagens com quatro ou mais tolerâncias.

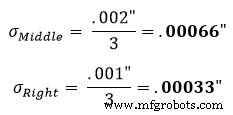
Antes de iniciar uma análise estatística de tolerância, você deve calcular ou escolher um fator de distribuição de tolerância. A distribuição padrão é 3 . Isso significa que a maioria dos dados (ou, neste caso, as tolerâncias) estarão dentro de 3 desvios padrão da média. Os desvios padrão de todas as tolerâncias devem ser divididos por este fator de distribuição de tolerância para normalizá-los de uma distribuição de 3 para uma distribuição de 1 . Uma vez feito isso, a raiz quadrada da soma pode ser calculada para encontrar o desvio padrão da montagem.

Pense nisso como uma xícara de café sendo feita com 3 grãos de tamanhos diferentes. Para fazer uma deliciosa xícara de café, você deve primeiro moer todos os grãos no mesmo tamanho para que possam ser adicionados ao filtro de café. Nesse caso, os grãos são os desvios padrão, o moedor é o fator de distribuição de tolerância e o filtro de café é a equação da soma da raiz quadrada. Isso é necessário porque algumas tolerâncias podem ter diferentes fatores de distribuição com base no aperto da faixa de tolerância.

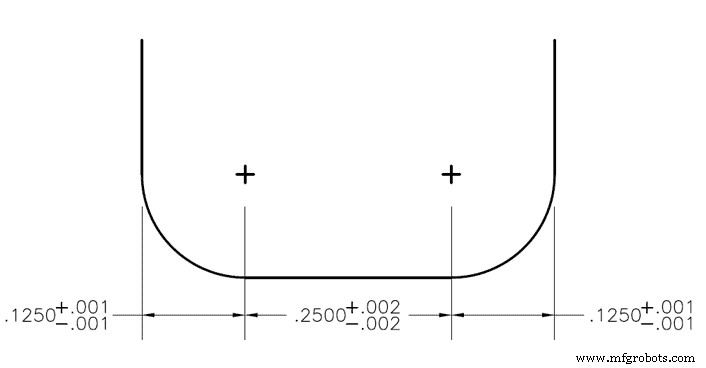
O método de análise estatística é usado se houver a exigência de que o slot tenha 0,500" de largura com uma tolerância de +/- 0,003", mas não há necessidade de raios (0,125") e plano (0,250" ) para ser exato, desde que caibam no slot. Neste exemplo, temos 3 tolerâncias bilaterais com seus desvios padrão já disponíveis. Como eles são bilaterais, o desvio padrão da média seria simplesmente o valor de tolerância + ou –. Para os raios externos, isso seria 0,001” e para a região plana do meio seria 0,002”.

Para este exemplo, vamos encontrar o desvio padrão (σ) de cada seção usando a equação 1. Nesta equação representa o desvio padrão.

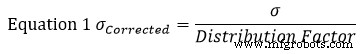
A suposição padrão é que uma tolerância de peça representa uma distribuição normal de +/- 3. Portanto, o fator de distribuição será 3. Usando a equação 1 na seção esquerda da figura 1, descobrimos que seu desvio padrão corrigido equivale a:

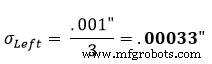
Isso é então repetido para as seções do meio e da direita:

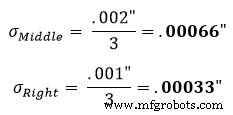
Depois de chegar a esses desvios padrão, inserimos os resultados na equação 2 para encontrar o desvio padrão da zona de tolerância. A equação 2 é conhecida como a equação da soma da raiz ao quadrado.

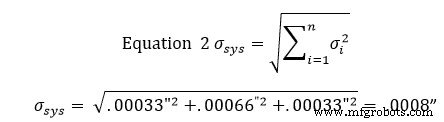
Neste ponto, significa que 68% dos slots estarão dentro de uma tolerância de +/- 0,0008”. Multiplicar essa tolerância por 2 resultará em uma janela de confiança de 95%, enquanto multiplicá-la por 3 resultará em uma janela de confiança de 99%.

68% dos slots estarão dentro de +/- .0008”

95% dos slots estarão dentro de +/- 0,0016”

99% dos slots estarão dentro de +/- 0,0024”

Essas janelas de confiança são padrão para um conjunto distribuído normal de pontos de dados. Uma distribuição normal padrão pode ser vista na Figura 2 acima.

A análise estatística de tolerância só deve ser usada para montagens com mais de 4 peças com tolerância. Muitos fatores foram ignorados nesta análise simples. Este exemplo foi para 3 dimensões bilaterais cujas tolerâncias eram representativas de seus desvios padrão de suas médias. Na análise de tolerância estatística padrão, outras variáveis ​​entram em jogo, como ângulos, excentricidade e paralelismo, que exigem fatores de correção.

Você sabia que a Harvey Performance Company Brands faz parceria com os principais fornecedores de software de câmera do setor para fornecer bibliotecas de ferramentas?

Clique aqui para saber mais

Use a análise do pior caso:

A análise do pior caso é a prática de somar todas as tolerâncias de uma peça para encontrar a tolerância total da peça. Ao realizar este tipo de análise, cada tolerância é definida em seu maior ou menor limite em sua respectiva faixa. Essa tolerância total pode ser comparada aos limites de desempenho da peça para garantir que a montagem seja projetada corretamente. Isso normalmente é usado para apenas 1 dimensão (apenas 1 plano, portanto, sem ângulos envolvidos) e para montagens com um pequeno número de peças.

A análise do pior caso também pode ser usada ao escolher a ferramenta de corte apropriada para o seu trabalho, pois a tolerância da ferramenta pode ser adicionada à tolerância das peças para o pior cenário. Uma vez identificado este cenário, o maquinista ou engenheiro pode fazer os devidos ajustes para manter a peça dentro das dimensões especificadas na impressão. Deve-se notar que o pior cenário raramente ocorre na produção real. Embora essas análises possam ser caras para a fabricação, elas proporcionam tranquilidade aos maquinistas, garantindo que todos os conjuntos funcionem corretamente. Muitas vezes, esse método requer tolerâncias rígidas porque o empilhamento total em condições máximas é o principal recurso usado no projeto. Tolerâncias mais apertadas intensificam os custos de fabricação devido ao aumento da quantidade de raspagem, tempo de produção para inspeção e custo do ferramental usado nessas peças.

Exemplo do pior cenário no contexto da Figura 1:

Encontre o limite inferior de especificação.

Para o raio do canto esquerdo

0,125” – 0,001” =0,124”

Para a seção plana

0,250” – 0,002” =0,248”

Para o raio do canto direito

0,125” – 0,001” =0,124”

Adicione tudo isso ao limite de especificação inferior:

0,124" + 0,248" + 0,124" =0,496"

Encontre o limite superior de especificação:

Para o raio do canto esquerdo

0,125" + 0,001" =0,126"

Para a seção plana

0,250" + 0,002" =0,252"

Para o raio do canto direito

0,125" + 0,001" =0,126"

Adicione tudo isso ao limite de especificação inferior:

0,126" + 0,252" + 0,126" =0,504"

Subtraia os dois e divida esta resposta por dois para obter a tolerância do pior caso:

(Limite Superior - Limite Inferior)/2 =0,004"

Portanto, o pior cenário deste slot é 0,500” +/- 0,004”.