O que é a transformada de Fourier?

Este artigo fornece informações essenciais sobre uma técnica matemática que desempenha um papel absolutamente fundamental no projeto do sistema e no processamento de sinais.

Nomeada em homenagem ao matemático francês Joseph Fourier, a transformada de Fourier é um procedimento matemático que nos permite determinar o conteúdo da frequência de uma função. Para engenheiros elétricos, a transformada de Fourier é normalmente aplicada a funções de tempo que chamamos de sinais .

Decomposição sinusoidal

Um gráfico de tensão ou corrente vs. tempo, como veríamos em uma tela de osciloscópio, é uma representação intuitiva do comportamento do sinal. Não é, no entanto, a única representação útil.

Em muitos casos - por exemplo, no projeto de sistemas de RF - estamos interessados ​​principalmente no comportamento periódico dos sinais. Mais especificamente, estamos interessados ​​em compreender um sinal em relação a senoidal periodicidade, porque os sinusóides são a expressão matemática única da frequência “pura”.

A transformada de Fourier revela a periodicidade elementar de um sinal por decomposição o sinal em suas frequências sinusoidais constituintes e identificando as magnitudes e fases dessas frequências constituintes.

A palavra “decomposição” é crucial aqui. A transformada de Fourier nos ensina a pensar sobre um sinal no domínio do tempo como uma forma de onda que é composta por formas de onda senoidais subjacentes com várias magnitudes e fases.

Uma onda quadrada, por exemplo, pode ser decomposta em uma série infinita de sinusóides com amplitudes que diminuem continuamente e frequências que aumentam continuamente. A série exata, para uma onda quadrada acoplada AC de período T e amplitude A, pode ser escrita da seguinte forma:

\ [f_ {square} (t) =\ frac {4A} {\ pi} \ sum_ {k \ in {\ {1,3,5, ... \ }}} \ frac {1} {k} \ sin \ left (\ frac {2 \ pi kt} {T} \ right) \]

Podemos converter isso para a seguinte forma, que é um pouco mais intuitiva:

\ [f_ {square} (t) =\ frac {4A} {\ pi} \ left (\ sin (2 \ pi ft) + \ frac {1} {3 } \ sin (6 \ pi ft) + \ frac {1} {5} \ sin (10 \ pi ft) + \ ... \ right) \]

onde f é a frequência, em hertz, da onda quadrada.

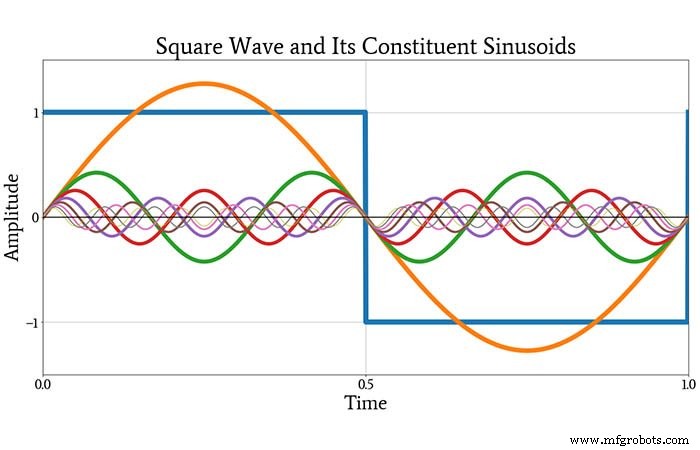
O gráfico a seguir mostra a onda quadrada original, em azul, e as primeiras oito sinusóides na série infinita.

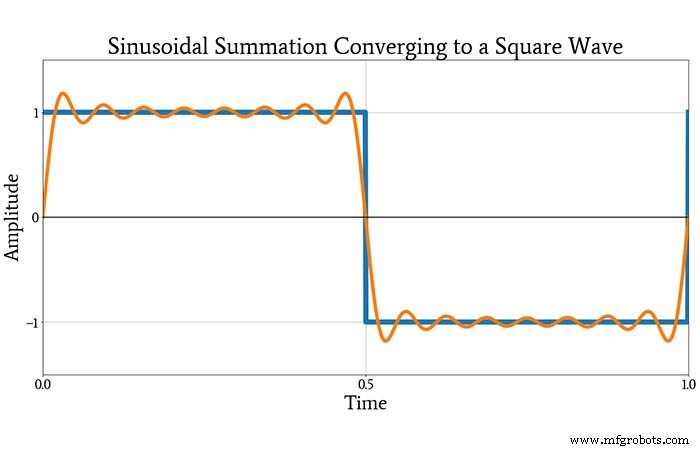
Depois de olhar para este gráfico, você ainda pode estar um pouco cético de que esses sinusóides possam ser combinados em uma onda quadrada. A próxima trama irá convencê-lo, entretanto. Mostra a onda quadrada original e a forma de onda produzida pela adição todos os sinusóides constituintes mostrados acima.

Funções de tempo e frequência

Quando calculamos uma transformada de Fourier, começamos com uma função de tempo, f (t), e por meio da decomposição matemática, produzimos uma função de frequência, F (ω). (Normalmente usamos frequência angular em discussões teóricas da transformada de Fourier.)

Avaliando F (ω) em alguma frequência angular específica, digamos 100 rad / s, nos dá a magnitude e a fase da componente senoidal de f (t) que tem uma frequência de 100 rad / s. Se f (t) não tiver um componente senoidal a 100 rad / s, a magnitude será zero.

Você deve estar se perguntando como uma função, F (ω), pode relatar magnitude e fase. A transformação de Fourier produz um valor complexo função, o que significa que a própria transformação não é nem a magnitude dos componentes de frequência em f (t), nem a fase desses componentes. Como acontece com qualquer número complexo, devemos realizar cálculos adicionais para extrair a magnitude ou a fase.

O conceito de uma transformação de valor complexo é um pouco mais intuitivo quando estamos trabalhando com um discreto Transformada de Fourier, ao invés de uma transformação “padrão” na qual começamos com uma função simbólica de tempo e terminamos com uma função simbólica de frequência.

A transformada discreta de Fourier opera em uma sequência de valores numéricos e produz uma sequência de coeficientes de Fourier . Esses coeficientes são números complexos típicos (ou seja, eles têm a forma a + jb), e geralmente usamos a magnitude desses números complexos, calculados como √ (a ² + b ² ), ao analisar o conteúdo de frequência de um sinal.

Traçando a transformada de Fourier

Plotagens de conteúdo de frequência são extremamente comuns em planilhas de dados, relatórios de teste, livros didáticos e assim por diante. Freqüentemente nos referimos a um gráfico de magnitude vs. frequência como um espectro - por exemplo, “vamos dar uma olhada no espectro do sinal” significa “vamos dar uma olhada em algum tipo de representação visual da informação de magnitude na transformada de Fourier . ”

O gráfico a seguir mostra o espectro de uma onda quadrada acoplada a CA com uma amplitude de 1 e uma frequência de 1 Hz.

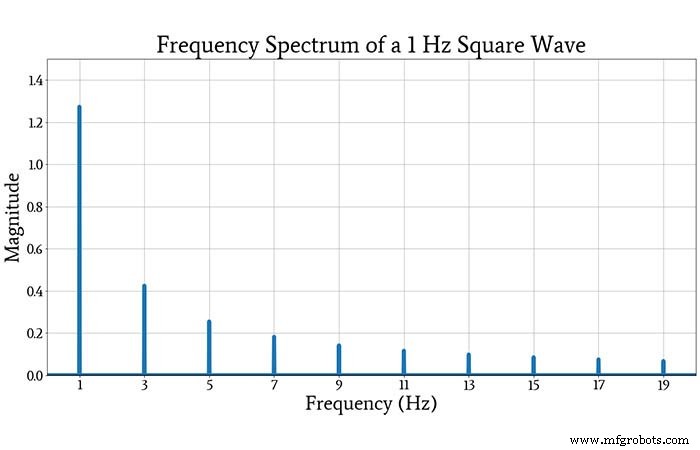
Se você comparar as amplitudes plotadas dos “picos” de frequência com as amplitudes dos componentes sinusoidais correspondentes na série infinita discutida acima, verá que eles são consistentes.

Calculando a transformada de Fourier

Estamos quase no final deste artigo e ainda não contei como realmente geramos a transformada de Fourier de um sinal definido matematicamente.

Para ser honesto, não vejo necessidade de explorar detalhadamente os detalhes matemáticos em um artigo introdutório:a análise no domínio da frequência hoje em dia é dominada por técnicas fáceis de usar e baseadas em software, e os engenheiros não gastam muito tempo convertendo tempo simbólico expressões de domínio em expressões de domínio de frequência simbólica.

No entanto, com algo tão importante como a transformada de Fourier, é bom pelo menos estar ciente da matemática subjacente. Então, sem mais delongas, é assim que convertemos f (t) em F (ω):

\ [F (\ omega) =\ int \ limits_ {- \ infty} ^ {+ \ infty} {f (t) {e ^ {- j \ omega t} } dt} \]

Conclusão

Espero que este artigo tenha fornecido uma explicação clara e intuitiva do que é a transformada de Fourier e como ela nos dá uma visão adicional sobre a natureza de um sinal.

A transformação de Fourier é apenas o começo de uma ampla gama de tópicos relacionados; se quiser saber mais, dê uma olhada nos artigos listados abaixo.

Leitura Adicional

• Uma introdução à transformada discreta de Fourier
• Uma introdução à transformada rápida de Fourier
• Como realizar análises de domínio de frequência com o Scilab
• Aprendendo a viver no domínio da frequência
• Filtragem linear baseada na transformada discreta de Fourier