Capacitores e cálculo

Os capacitores não têm uma “resistência” estável como os condutores. No entanto, existe uma relação matemática definitiva entre a tensão e a corrente para um capacitor, como segue:



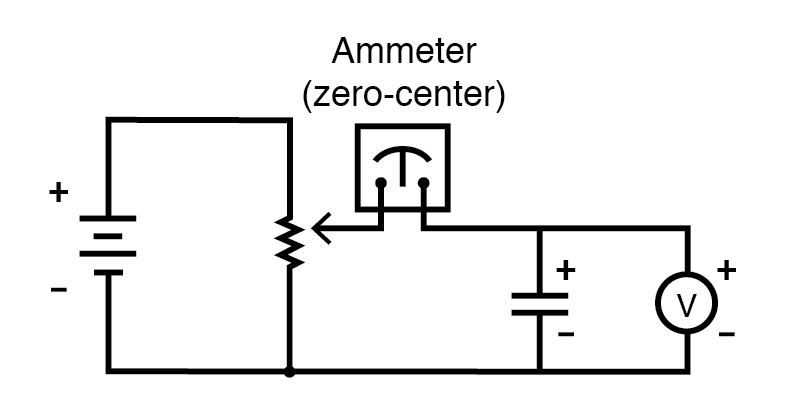
A letra minúscula “i” simboliza instantâneo corrente, que significa a quantidade de corrente em um ponto específico no tempo. Isso contrasta com a corrente constante ou corrente média (letra maiúscula “I”) por um período de tempo não especificado. A expressão "dv / dt" é emprestada do cálculo, significando a taxa instantânea de mudança de voltagem ao longo do tempo, ou a taxa de mudança de voltagem (aumento ou diminuição de volts por segundo) em um ponto específico no tempo, o mesmo ponto específico em tempo em que a corrente instantânea é referenciada. Por algum motivo, a letra v geralmente é usado para representar a tensão instantânea em vez da letra e . No entanto, não seria incorreto expressar a taxa de variação da tensão instantânea como “de / dt”.

Nesta equação, vemos algo novo em nossa experiência até agora com circuitos elétricos:a variável de tempo . Ao relacionar as quantidades de tensão, corrente e resistência a um resistor, não importa se estamos lidando com medições feitas ao longo de um período de tempo não especificado (E =IR; V =IR), ou em um momento específico em tempo (e =ir; v =ir). A mesma fórmula básica é válida, porque o tempo é irrelevante para a voltagem, corrente e resistência em um componente como um resistor.

Em um capacitor, no entanto, o tempo é uma variável essencial, porque a corrente está relacionada a quão rapidamente a tensão muda com o tempo. Para entender isso completamente, algumas ilustrações podem ser necessárias. Suponha que conectemos um capacitor a uma fonte de tensão variável, construída com um potenciômetro e uma bateria:



Se o mecanismo do potenciômetro permanecer em uma única posição (o limpador está estacionário), o voltímetro conectado ao capacitor registrará uma tensão constante (inalterada) e o amperímetro registrará 0 amperes. Nesse cenário, a taxa instantânea de mudança de tensão (dv / dt) é igual a zero, porque a tensão é imutável. A equação nos diz que com 0 volts por segundo de mudança para um dv / dt, deve haver zero correntes instantâneas (i). De uma perspectiva física, sem mudança na voltagem, não há necessidade de qualquer movimento do elétron para adicionar ou subtrair carga das placas do capacitor e, portanto, não haverá corrente.



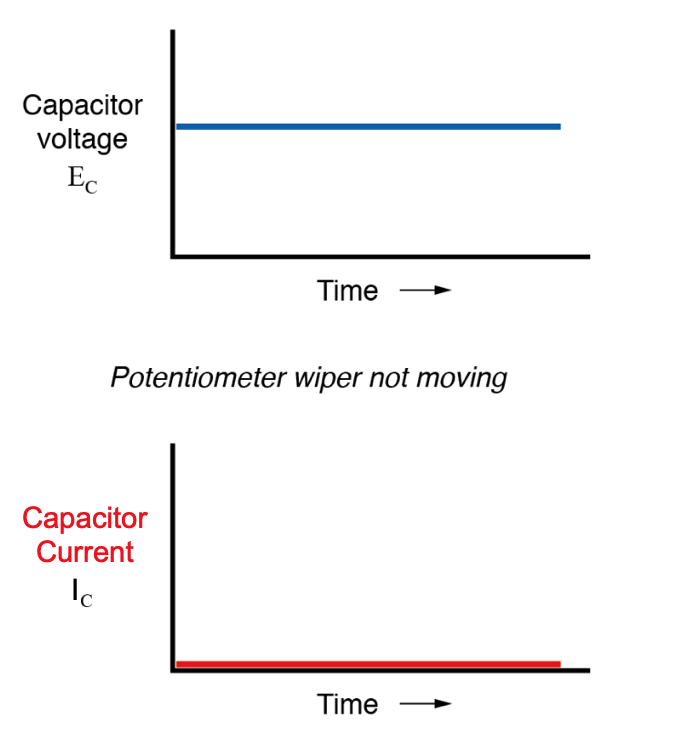
Agora, se o limpador do potenciômetro for movido lenta e continuamente na direção “para cima”, uma tensão maior será gradualmente imposta ao capacitor. Assim, a indicação do voltímetro aumentará em uma taxa lenta:



Se assumirmos que o limpador do potenciômetro está sendo movido de forma que a taxa Se o aumento da tensão no capacitor for estável (por exemplo, a tensão aumentando a uma taxa constante de 2 volts por segundo), o termo dv / dt da fórmula será um valor fixo. De acordo com a equação, este valor fixo de dv / dt, multiplicado pela capacitância do capacitor em Farads (também fixa), resulta em uma corrente fixa de alguma magnitude. De uma perspectiva física, uma tensão crescente no capacitor exige que haja um diferencial de carga crescente entre as placas. Portanto, para uma taxa de aumento de tensão lenta e constante, deve haver uma taxa lenta e constante de carga no capacitor, que equivale a um fluxo de corrente lento e constante. Neste cenário, o capacitor está carregando e agindo como uma carga , com a corrente entrando na placa positiva e saindo da placa negativa à medida que o capacitor acumula energia em um campo elétrico.



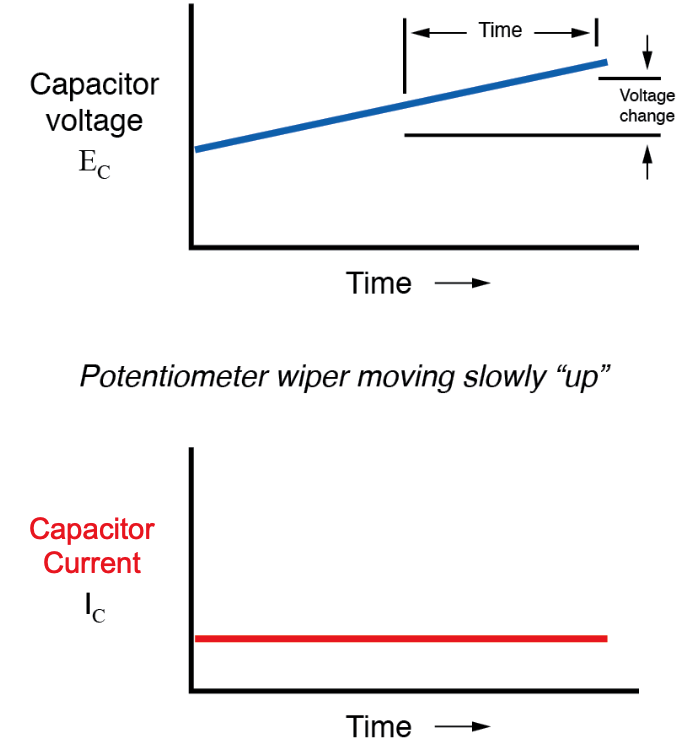
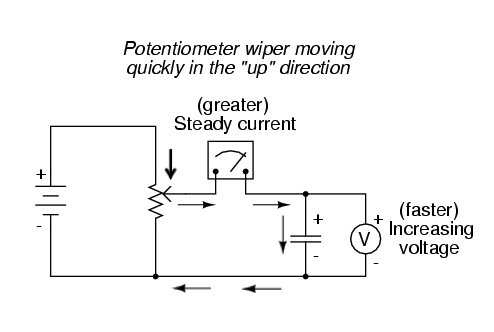
Se o potenciômetro for movido na mesma direção, mas em uma taxa mais rápida, a taxa de mudança de voltagem (dv / dt) será maior e assim será a corrente do capacitor:

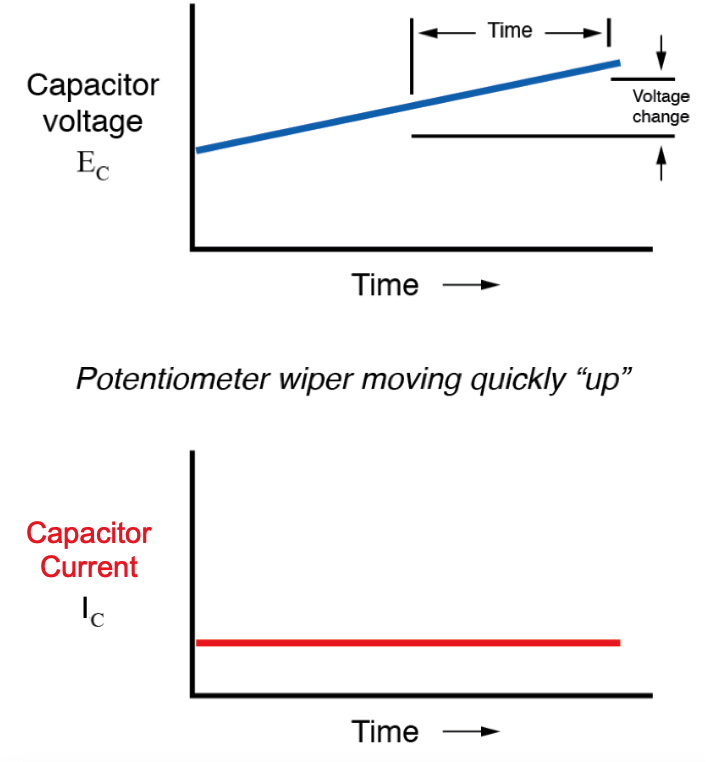
Quando os alunos de matemática estudam cálculo pela primeira vez, eles começam explorando o conceito de taxas de mudança para várias funções matemáticas. A derivada , que é o primeiro e mais elementar princípio de cálculo, é uma expressão da taxa de variação de uma variável em termos de outra. Os alunos de cálculo precisam aprender este princípio enquanto estudam equações abstratas. Você aprende esse princípio enquanto estuda algo com o qual se identifica:circuitos elétricos!

Para colocar essa relação entre tensão e corrente em um capacitor em termos de cálculo, a corrente através de um capacitor é a derivada da tensão através do capacitor em relação ao tempo. Ou, afirmado em termos mais simples, a corrente de um capacitor é diretamente proporcional à rapidez com que a tensão através dele está mudando. Neste circuito onde a tensão do capacitor é definida pela posição de um botão rotativo em um potenciômetro, podemos dizer que a corrente do capacitor é diretamente proporcional à rapidez com que giramos o botão.

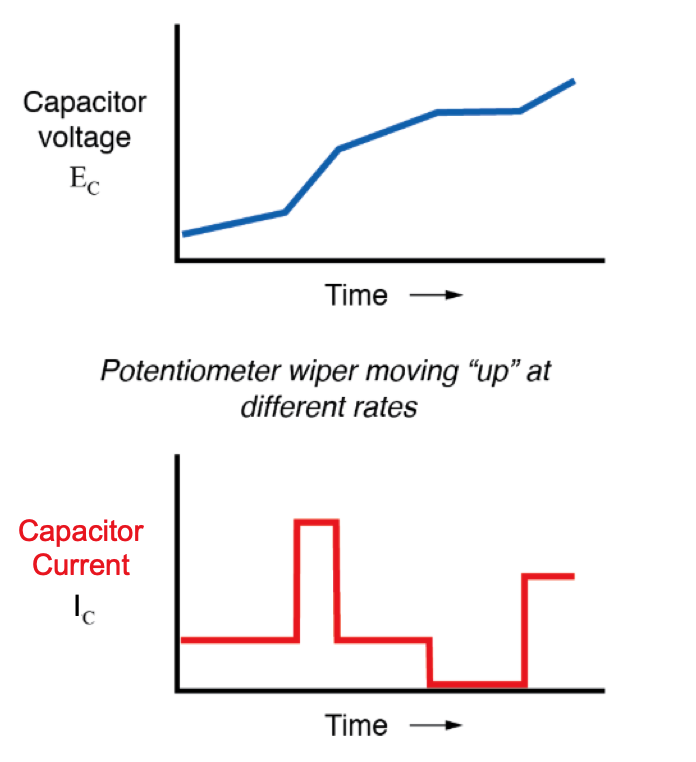
Se movêssemos o limpador do potenciômetro na mesma direção de antes ("para cima"), mas em taxas variáveis, obteríamos gráficos semelhantes a este:



Observe que em qualquer ponto no tempo, a corrente do capacitor é proporcional à taxa de mudança, ou inclinação , do gráfico de tensão do capacitor. Quando a linha do gráfico de tensão está subindo rapidamente (declive acentuado), a corrente também será grande. Onde o gráfico de tensão tem uma inclinação moderada, a corrente é pequena. Em um lugar no gráfico de tensão onde se nivela (inclinação zero, representando um período de tempo em que o potenciômetro não estava se movendo), a corrente cai para zero.

Se movêssemos o limpador do potenciômetro na direção "para baixo", a tensão do capacitor diminuiria em vez de aumentar. Novamente, o capacitor reagirá a essa mudança de voltagem produzindo uma corrente, mas desta vez a corrente estará na direção oposta. A diminuição da tensão do capacitor requer que o diferencial de carga entre as placas do capacitor seja reduzido, e a única maneira de isso acontecer é se a direção do fluxo da corrente for invertida, com o capacitor descarregando em vez de carregando. Nesta condição de descarga, com a corrente saindo da placa positiva e entrando na placa negativa, o capacitor atuará como uma fonte , como uma bateria, liberando sua energia armazenada para o resto do circuito.



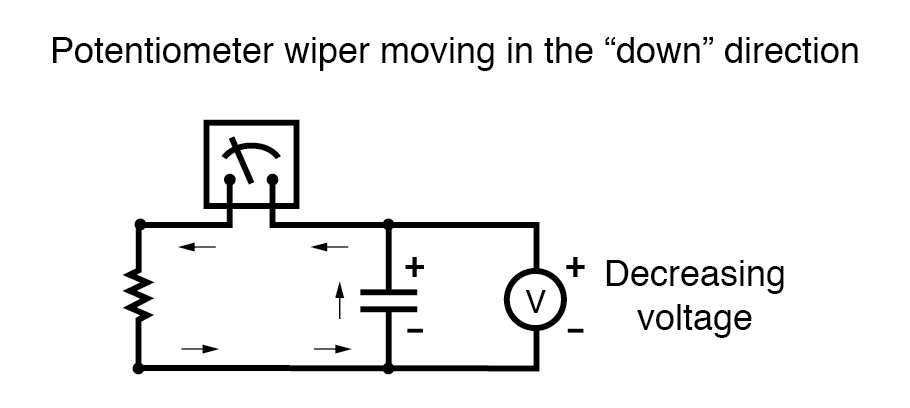
Novamente, a quantidade de corrente que passa pelo capacitor é diretamente proporcional à taxa de variação da voltagem. A única diferença entre os efeitos de uma diminuição voltagem e um crescente tensão é a direção do fluxo atual. Para a mesma taxa de mudança de tensão ao longo do tempo, aumentando ou diminuindo, a magnitude da corrente (amperes) será a mesma. Matematicamente, uma taxa de variação de voltagem decrescente é expressa como um negativo quantidade dv / dt. Seguindo a fórmula i =C (dv / dt), isso resultará em um valor de corrente (i) que é igualmente negativo em sinal, indicando uma direção de fluxo correspondente à descarga do capacitor.

PLANILHAS RELACIONADAS:

• Planilha de capacitores
• Planilha de cálculo para circuitos elétricos