Cálculos de tensão e corrente

Existe uma maneira de calcular qualquer um dos valores em um circuito CC reativo ao longo do tempo.

Cálculo de valores em um circuito CC reativo

O primeiro passo é identificar os valores inicial e final para qualquer quantidade em que o capacitor ou indutor se opõe à mudança; isto é, qualquer quantidade que o componente reativo está tentando manter constante. Para capacitores, esta quantidade é tensão ; para indutores, esta quantidade é atual . Quando a chave em um circuito é fechada (ou aberta), o componente reativo tentará manter essa quantidade no mesmo nível que estava antes da transição da chave, de forma que esse valor seja usado para o valor “inicial”.

O valor final para essa quantidade é qualquer que seja essa quantidade depois de um período infinito de tempo. Isso pode ser determinado analisando um circuito capacitivo, como se o capacitor fosse um circuito aberto, e um circuito indutivo, como se o indutor fosse um curto-circuito, porque é assim que esses componentes se comportam quando atingem a "carga total", depois de uma quantidade infinita de tempo.

A próxima etapa é calcular a constante de tempo do circuito:a quantidade de tempo que leva para os valores de tensão ou corrente mudarem aproximadamente 63 por cento de seus valores iniciais para seus valores finais em uma situação transitória.

Em um circuito RC em série, a constante de tempo é igual à resistência total em ohms multiplicada pela capacitância total em farads. Para um circuito série L / R, é a indutância total em henrys dividida pela resistência total em ohms. Em qualquer caso, a constante de tempo é expressa em unidades de segundos e simbolizado pela letra grega "tau" (τ):







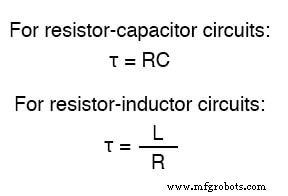
O aumento e a queda dos valores do circuito, como tensão e corrente em resposta a um transiente, são, como foi mencionado antes, assintóticos . Sendo assim, os valores começam a mudar rapidamente logo após o transiente e se estabilizam com o tempo. Se plotados em um gráfico, a abordagem para os valores finais de tensão e corrente formam curvas exponenciais.

Como foi dito antes, uma constante de tempo é a quantidade de tempo que leva para qualquer um desses valores mudar cerca de 63 por cento de seus valores iniciais para seus valores finais (finais). Para cada constante de tempo, esses valores se movem (aproximadamente) 63 por cento mais perto de sua meta final. A fórmula matemática para determinar a porcentagem precisa é bastante simples:







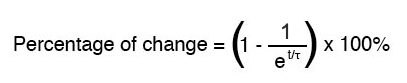
A letra e representa a constante de Euler, que é aproximadamente 2,7182818. É derivado de técnicas de cálculo, depois de analisar matematicamente a abordagem assintótica dos valores do circuito. Após uma constante de tempo, a porcentagem de mudança do valor inicial para o valor final é:







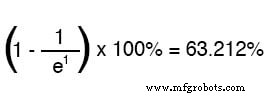
Após o valor de duas constantes de tempo de tempo, a porcentagem de mudança do valor inicial ao valor final é:







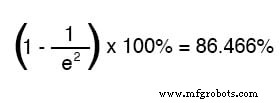
Após dez constantes de tempo, a porcentagem é:







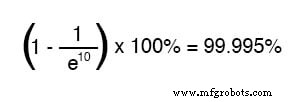
Quanto mais tempo passa desde a aplicação transitória da tensão da bateria, maior será o valor do denominador na fração, o que resulta em um valor menor para toda a fração, o que resulta em um total geral (1 menos a fração) se aproximando 1 ou 100 por cento.

Fórmula da constante de tempo universal

Podemos fazer uma fórmula mais universal com esta para a determinação dos valores de tensão e corrente em circuitos transitórios, multiplicando esta quantidade pela diferença entre os valores do circuito inicial e final:





Vamos analisar o aumento de tensão no circuito resistor-capacitor em série mostrado no início do capítulo.







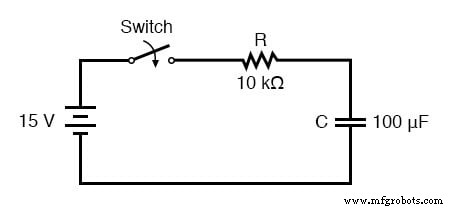
Observe que estamos escolhendo analisar a tensão porque essa é a quantidade que os capacitores tendem a se manter constantes. Embora a fórmula funcione muito bem para a corrente, os valores inicial e final para a corrente são, na verdade, derivados da tensão do capacitor, de modo que o cálculo da tensão é um método mais direto. A resistência é 10 kΩ e a capacitância é 100 µF (microfarads). Uma vez que a constante de tempo (τ) para um circuito RC é o produto da resistência e capacitância, obtemos um valor de 1 segundo:







Se o capacitor começa em um estado totalmente descarregado (0 volts), então podemos usar esse valor de tensão para um valor de “partida”. O valor final, é claro, será a tensão da bateria (15 volts). Nossa fórmula universal para a tensão do capacitor neste circuito é assim:







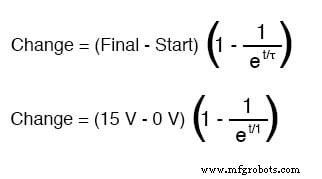
Portanto, após 7,25 segundos de aplicação de tensão através da chave fechada, a tensão do nosso capacitor terá aumentado em:







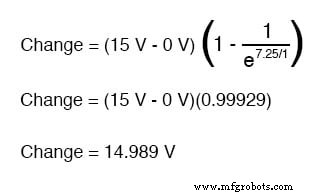
Como começamos com uma tensão de capacitor de 0 volts, esse aumento de 14.989 volts significa que temos 14.989 volts após 7,25 segundos.

A mesma fórmula funcionará para determinar a corrente nesse circuito também. Como sabemos que um capacitor descarregado inicialmente atua como um curto-circuito, a corrente de partida será a quantidade máxima possível:15 volts (da bateria) dividido por 10 kΩ (a única oposição à corrente no circuito no início):







Também sabemos que a corrente final será zero, já que o capacitor acabará se comportando como um circuito aberto, o que significa que, eventualmente, nenhum elétron fluirá no circuito. Agora que sabemos os valores de corrente inicial e final, podemos usar nossa fórmula universal para determinar a corrente após 7,25 segundos do fechamento da chave no mesmo circuito RC:







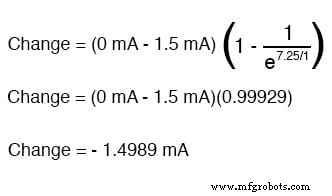
Observe que o valor obtido para a mudança é negativo, não positivo! Isso nos diz que a corrente diminuiu em vez de aumentar com o passar do tempo. Como começamos com uma corrente de 1,5 mA, essa diminuição (-1,4989 mA) significa que temos 0,001065 mA (1,065 µA) após 7,25 segundos.

Poderíamos também ter determinado a corrente do circuito no tempo =7,25 segundos subtraindo a tensão do capacitor (14,989 volts) da tensão da bateria (15 volts) para obter a queda de tensão através do resistor de 10 kΩ, então calculando a corrente através do resistor (e o circuito em série completo) com a Lei de Ohm (I =E / R). De qualquer forma, devemos obter a mesma resposta:

Usando a fórmula da constante de tempo universal para analisar circuitos indutivos

A fórmula da constante de tempo universal também funciona bem para analisar circuitos indutivos. Vamos aplicá-lo ao nosso circuito L / R de exemplo no início do capítulo:







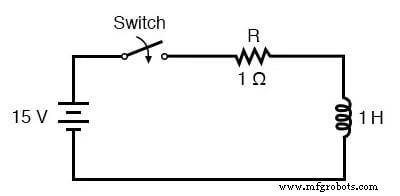
Com uma indutância de 1 Henry e uma resistência em série de 1 Ω, nossa constante de tempo é igual a 1 segundo:







Como este é um circuito indutivo, e sabemos que os indutores se opõem à mudança na corrente, vamos configurar nossa fórmula de constante de tempo para os valores inicial e final da corrente. Se começarmos com a chave na posição aberta, a corrente será igual a zero, portanto, zero é o nosso valor de corrente inicial.

Após a chave ter sido deixada fechada por um longo tempo, a corrente se estabilizará em seu valor final, igual à tensão da fonte dividida pela resistência total do circuito (I =E / R), ou 15 amperes no caso deste circuito .

Se desejássemos determinar o valor da corrente em 3,5 segundos, aplicaríamos a fórmula da constante de tempo universal como tal:







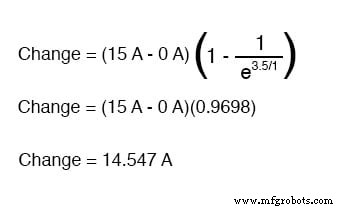
Dado o fato de que nossa corrente de partida era zero, isso nos deixa com uma corrente de circuito de 14,547 amperes a 3,5 segundos.

A determinação da tensão em um circuito indutivo é melhor realizada primeiro descobrindo a corrente do circuito e, em seguida, calculando as quedas de tensão nas resistências para encontrar o que sobrou para cair no indutor. Com apenas um resistor em nosso circuito de exemplo (tendo um valor de 1 Ω), isso é bastante fácil:





Subtraído da tensão de nossa bateria de 15 volts, isso deixa 0,453 volts no indutor no tempo =3,5 segundos.







REVER:

• Fórmula da constante de tempo universal:
• Para analisar um circuito RC ou L / R, siga estas etapas:
• (1):Determine a constante de tempo para o circuito (RC ou L / R).
• (2):Identifique a quantidade a ser calculada (qualquer quantidade cuja variação é diretamente oposta pelo componente reativo. Para capacitores, é a tensão; para os indutores, é a corrente).
• (3):Determine os valores inicial e final para aquela quantidade.
• (4):Insira todos esses valores (final, início, tempo, constante de tempo) na fórmula da constante de tempo universal e resolva para mudança em quantidade.
• (5):Se o valor inicial era zero, então o valor real na hora especificada é igual à mudança calculada dada pela fórmula universal. Caso contrário, adicione a alteração ao valor inicial para descobrir onde você está.

PLANILHAS RELACIONADAS:

• Planilha de circuitos da constante de tempo
• Planilha de cálculos da constante de tempo

Veja nossa coleção de Calculadoras de potência em nosso Ferramentas seção.