Aritmética de número complexo

Como os números complexos são entidades matemáticas legítimas, assim como os números escalares, eles podem ser adicionados, subtraídos, multiplicados, divididos, ao quadrado, invertidos e assim por diante, como qualquer outro tipo de número.

Algumas calculadoras científicas são programadas para realizar diretamente essas operações em dois ou mais números complexos, mas essas operações também podem ser feitas "à mão". Esta seção mostrará como as operações básicas são realizadas.

É altamente Recomendamos que você se equipe com uma calculadora científica capaz de realizar funções aritméticas facilmente em números complexos. Isso tornará seu estudo do circuito AC muito mais agradável do que se você fosse forçado a fazer todos os cálculos da maneira mais longa.

Adição e subtração de números complexos na forma retangular

A adição e subtração com números complexos na forma retangular são fáceis. Além disso, basta somar os componentes reais dos números complexos para determinar o componente real da soma e somar os componentes imaginários dos números complexos para determinar o componente imaginário da soma:







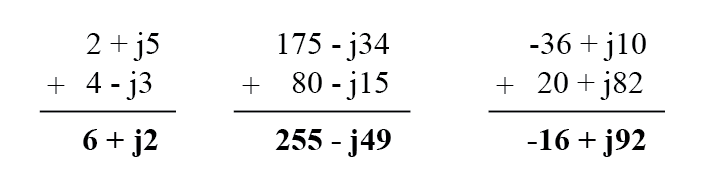
Ao subtrair números complexos na forma retangular, simplesmente subtraia o componente real do segundo número complexo do componente real do primeiro para chegar ao componente real da diferença e subtraia o componente imaginário do segundo número complexo do componente imaginário de o primeiro a chegar ao componente imaginário da diferença:

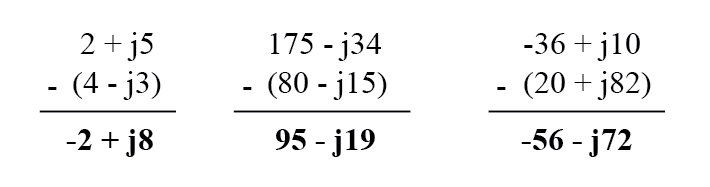
Multiplicação e divisão de números complexos na forma polar

Para multiplicação e divisão à mão, polar é a notação preferida para trabalhar. Ao multiplicar números complexos na forma polar, simplesmente multiplique as magnitudes polares dos números complexos para determinar a magnitude polar do produto e adicionar os ângulos dos números complexos para determinar o ângulo do produto:







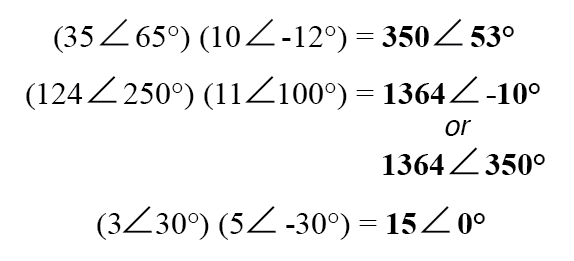
A divisão de números complexos na forma polar também é fácil:simplesmente divida a magnitude polar do primeiro número complexo pela magnitude polar do segundo número complexo para chegar à magnitude polar do quociente e subtraia o ângulo do segundo número complexo de o ângulo do primeiro número complexo para chegar ao ângulo do quociente:







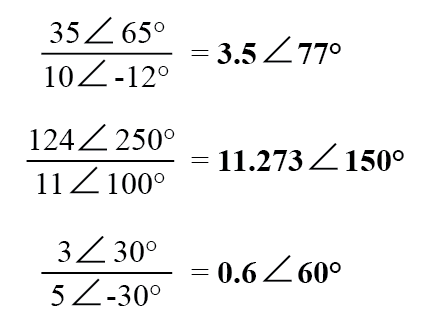
Para obter o recíproco, ou "inverter" (1 / x), um número complexo, basta dividir o número (na forma polar) em um valor escalar de 1, que nada mais é do que um número complexo sem componente imaginário (ângulo =0):







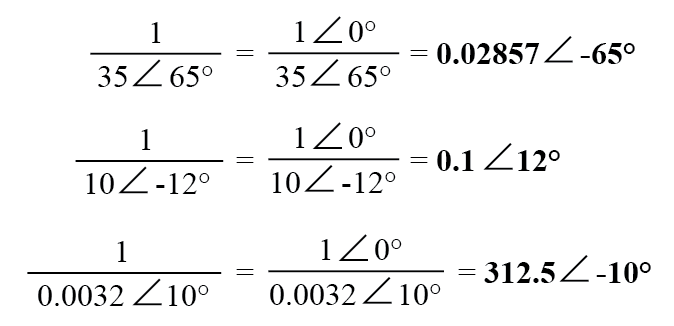
Estas são as operações básicas que você precisa saber para manipular números complexos na análise de circuitos CA. No entanto, as operações com números complexos não são de forma alguma limitadas apenas à adição, subtração, multiplicação, divisão e inversão.

Praticamente qualquer operação aritmética que pode ser feita com números escalares pode ser feita com números complexos, incluindo potências, raízes, resolução de equações simultâneas com coeficientes complexos e até mesmo funções trigonométricas (embora isso envolva uma perspectiva totalmente nova em trigonometria chamada funções hiperbólicas que está bem além do escopo desta discussão).

Certifique-se de estar familiarizado com as operações aritméticas básicas de adição, subtração, multiplicação, divisão e inversão, e você terá poucos problemas com a análise de circuito AC.



REVER:

• Para adicionar números complexos na forma retangular, adicione os componentes reais e adicione os componentes imaginários. A subtração é semelhante.
• Para multiplicar números complexos na forma polar, multiplique as magnitudes e adicione os ângulos. Para dividir, divida as magnitudes e subtraia um ângulo do outro.

PLANILHA RELACIONADA:

• Planilha da fase AC