Aritmética Booleana

Vamos começar nossa exploração da álgebra booleana adicionando números:







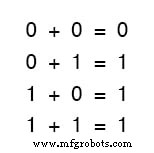
As três primeiras somas fazem todo o sentido para qualquer pessoa familiarizada com a adição elementar.

A última soma, entretanto, é possivelmente responsável por mais confusão do que qualquer outra afirmação isolada em eletrônica digital, porque parece ir contra os princípios básicos da matemática.

Bem, isso contradiz os princípios de adição para números reais, mas não para números booleanos.

Lembre-se de que, no mundo da álgebra booleana, existem apenas dois valores possíveis para qualquer quantidade e para qualquer operação aritmética:1 ou 0.

Não existe "2" no escopo dos valores booleanos. Uma vez que a soma "1 + 1" certamente não é 0, deve ser 1 por processo de eliminação.

Não importa quantos ou poucos termos adicionamos, também. Considere as seguintes somas:

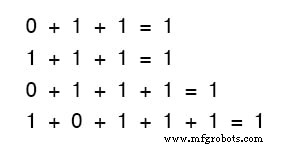
OU portão

Dê uma olhada nas somas de dois termos no primeiro conjunto de equações.

Esse padrão parece familiar para você? Deveria! É o mesmo padrão de 1 e 0 visto na tabela verdade para uma porta OR.

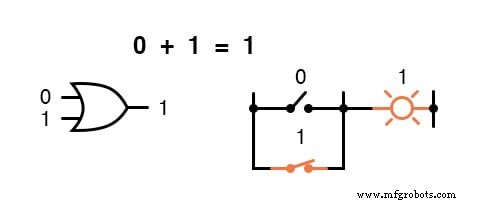
Em outras palavras, a adição booleana corresponde à função lógica de uma porta "OU", bem como aos contatos da chave paralela:













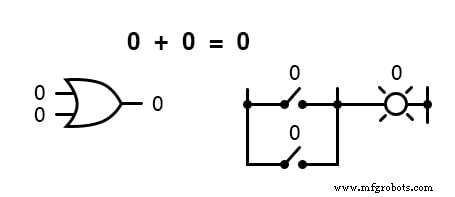
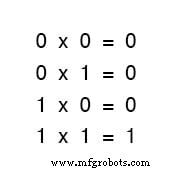
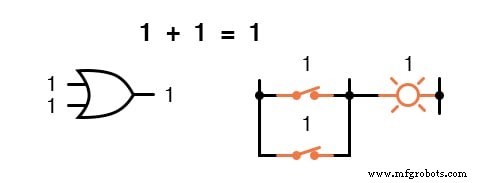
Não existe subtração no domínio da matemática booleana.

A subtração implica a existência de números negativos: 5 - 3 é o mesmo que 5 + (-3) , e na álgebra booleana, quantidades negativas são proibidas.

Também não existe divisão na matemática booleana, uma vez que a divisão nada mais é do que subtração composta , da mesma forma que a multiplicação é adição composta .

E portão

A multiplicação é válida na álgebra booleana e, felizmente, é a mesma que na álgebra de números reais:qualquer coisa multiplicada por 0 é 0 , e qualquer coisa multiplicada por 1 permanece inalterado:







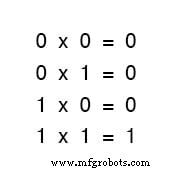
Este conjunto de equações também deve ser familiar para você:é o mesmo padrão encontrado na tabela verdade para uma porta AND.

Em outras palavras, a multiplicação booleana corresponde à função lógica de um “ AND ”Portão, bem como para contatos de comutação em série:













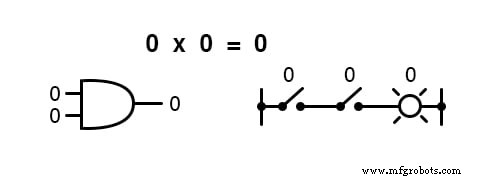
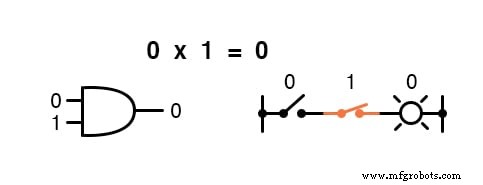
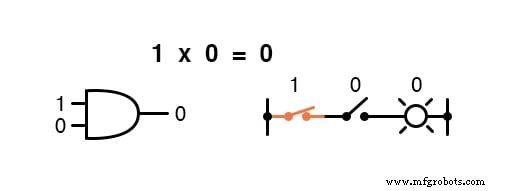
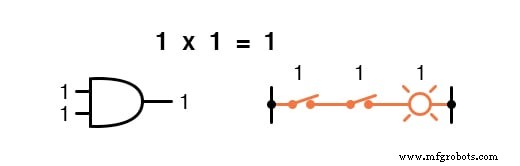
Como a álgebra “normal”, a álgebra booleana usa letras do alfabeto para denotar variáveis.

Ao contrário da álgebra “normal”, porém, as variáveis ​​booleanas são sempre letras MAIÚSCULAS, nunca minúsculas.

Porque eles podem possuir apenas um dos dois valores possíveis, 1 ou 0 , cada variável tem um complemento :o oposto de seu valor.

Por exemplo, se a variável “ A ”Tem um valor de 0 , então o complemento de A tem um valor de 1 .

A notação booleana usa uma barra acima do caractere variável para denotar complementação, assim:

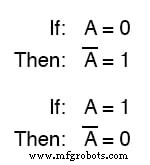
NÃO Gate

Na forma escrita, o complemento de “ A ”Denotado como“ A-not ”Ou“ A-bar ”. Às vezes, um símbolo “primo” é usado para representar a complementação.

Por exemplo, A 'Seria o complemento de A , o mesmo que usar um símbolo primo para denotar a diferenciação no cálculo, em vez da notação fracionária d / dt .

Normalmente, porém, o símbolo "barra" é mais amplamente utilizado do que o símbolo " primo ”, Por motivos que se tornarão mais evidentes posteriormente neste capítulo.

A complementação booleana encontra equivalência na forma da porta NOT , ou um interruptor normalmente fechado ou contato de relé:









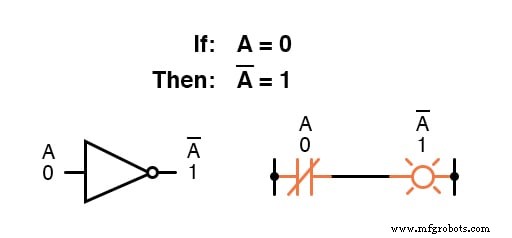
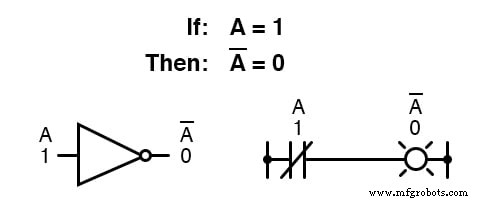
A definição básica de quantidades booleanas levou às regras simples de adição e multiplicação e excluiu a subtração e a divisão como operações aritméticas válidas.

Temos uma simbologia para denotar variáveis ​​booleanas e seus complementos. Na próxima seção, prosseguiremos com o desenvolvimento de identidades booleanas.



REVER:

• A adição booleana é equivalente a OU função lógica, bem como contatos de comutação paralelos.
• A multiplicação booleana é equivalente a E função lógica, bem como contatos de comutação em série.
• A complementação booleana é equivalente a NÃO função lógica, bem como normalmente fechado contatos de retransmissão.

PLANILHAS RELACIONADAS:

• Planilha de álgebra booleana