Compreendendo os mínimos locais no treinamento de rede neural

Este artigo discute uma complicação que pode impedir que seu Perceptron alcance a precisão de classificação adequada.

Na série de redes neurais AAC, cobrimos uma ampla gama de assuntos relacionados à compreensão e ao desenvolvimento de redes neurais Perceptron multicamadas. Antes de ler este artigo sobre mínimos locais, acompanhe o restante da série abaixo:

1. Como realizar a classificação usando uma rede neural:o que é o Perceptron?
2. Como usar um exemplo de rede neural simples Perceptron para classificar dados
3. Como treinar uma rede neural Perceptron básica
4. Compreendendo o treinamento de rede neural simples
5. Uma introdução à teoria de treinamento para redes neurais
6. Compreendendo a taxa de aprendizagem em redes neurais
7. Aprendizado de máquina avançado com o Multilayer Perceptron
8. A função de ativação sigmóide:ativação em redes neurais multicamadas Perceptron
9. Como treinar uma rede neural multicamadas Perceptron
10. Noções básicas sobre fórmulas de treinamento e retropropagação para percepções multicamadas
11. Arquitetura de rede neural para uma implementação Python
12. Como criar uma rede neural multicamadas Perceptron em Python
13. Processamento de sinais usando redes neurais:validação no projeto de redes neurais
14. Conjuntos de dados de treinamento para redes neurais:como treinar e validar uma rede neural Python
15. Quantas camadas e nós ocultos uma rede neural precisa?
16. Como aumentar a precisão de uma rede neural de camada oculta
17. Incorporação de nós de polarização em sua rede neural
18. Compreendendo os mínimos locais no treinamento de redes neurais

O treinamento de redes neurais é um processo complexo. Felizmente, não precisamos entendê-lo perfeitamente para nos beneficiarmos dele:as arquiteturas de rede e os procedimentos de treinamento que usamos realmente resultam em sistemas funcionais que alcançam uma precisão de classificação muito alta. No entanto, há um aspecto teórico do treinamento que, apesar de ser um tanto confuso, merece nossa atenção.

Vamos chamá-lo de “o problema dos mínimos locais”.

Por que os mínimos locais merecem nossa atenção?

Bem ... eu não tenho certeza. Quando eu aprendi sobre redes neurais, fiquei com a impressão de que mínimos locais realmente são um obstáculo significativo para o sucesso do treinamento, pelo menos quando estamos lidando com relações complexas de entrada e saída. No entanto, acredito que pesquisas recentes estão minimizando a importância dos mínimos locais. Talvez as novas estruturas de rede e técnicas de processamento tenham mitigado a gravidade do problema ou talvez simplesmente tenhamos um melhor entendimento de como as redes neurais realmente navegam em direção à solução desejada.

Revisaremos o status atual dos mínimos locais no final deste artigo. Por enquanto, vou responder minha pergunta da seguinte forma:mínimos locais merecem nossa atenção porque, primeiro, eles nos ajudam a pensar mais profundamente sobre o que realmente está acontecendo quando treinamos uma rede via gradiente descendente e, segundo, porque os mínimos locais são— ou pelo menos eram —Considerado um impedimento significativo para a implementação bem-sucedida de redes neurais em sistemas da vida real.

O que é um mínimo local?

Na Parte 5, consideramos a “tigela de erro” mostrada abaixo e descrevi o treinamento como essencialmente uma busca pelo ponto mais baixo desta tigela.

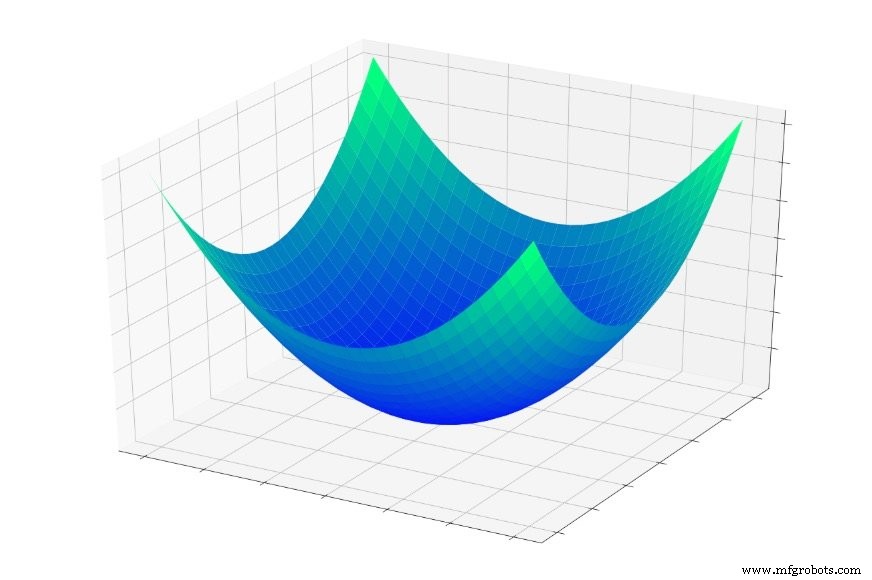
( Nota :Ao longo deste artigo, minhas imagens e explicações irão depender de nossa compreensão intuitiva de estruturas tridimensionais, mas tenha em mente que os conceitos gerais não se limitam a relações tridimensionais. Na verdade, frequentemente usamos redes neurais cuja dimensionalidade excede em muito duas variáveis ​​de entrada e uma variável de saída.)

Se você pular para dentro desta tigela, você deslizará para o fundo, todas as vezes. Não importa onde você comece , você acabará no ponto mais baixo de toda a função de erro. Este ponto mais baixo é o mínimo global . Quando uma rede convergiu para o mínimo global, ela otimizou sua capacidade de classificar os dados de treinamento e em teoria , este é o objetivo fundamental do treinamento:continuar modificando os pesos até que o mínimo global seja alcançado.

Sabemos, no entanto, que as redes neurais são capazes de aproximar relações extremamente complexas de entrada e saída. A tigela de erro acima não se encaixa exatamente na categoria "extremamente complexa". É simplesmente um gráfico da função \ (f (x, y) =x ^ 2 + y ^ 2 \).

Mas agora imagine que a função de erro se parece com isto:

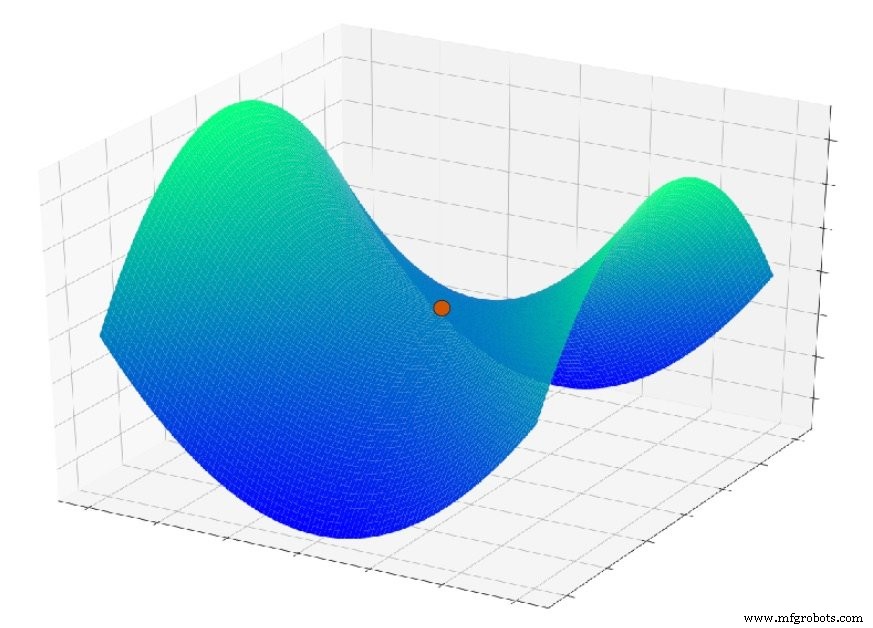
Ou isto:

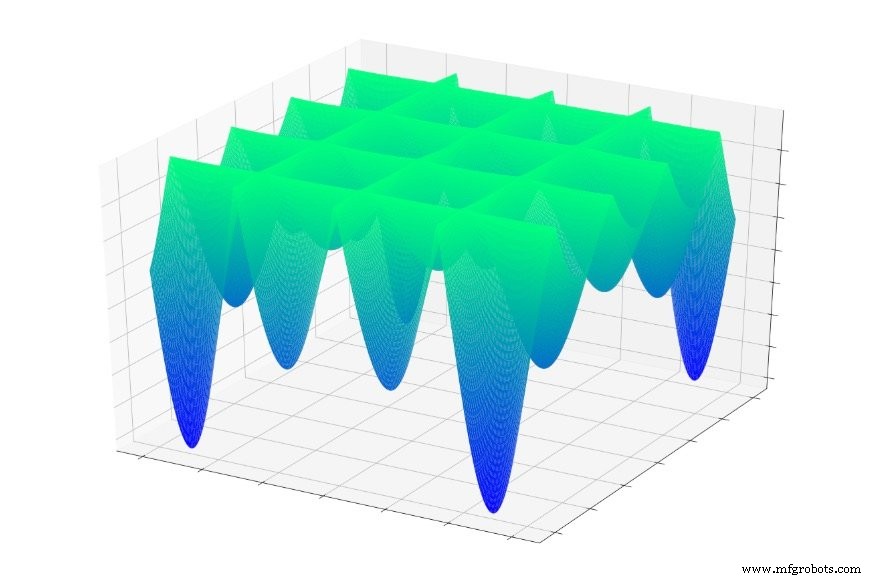
Ou isto:

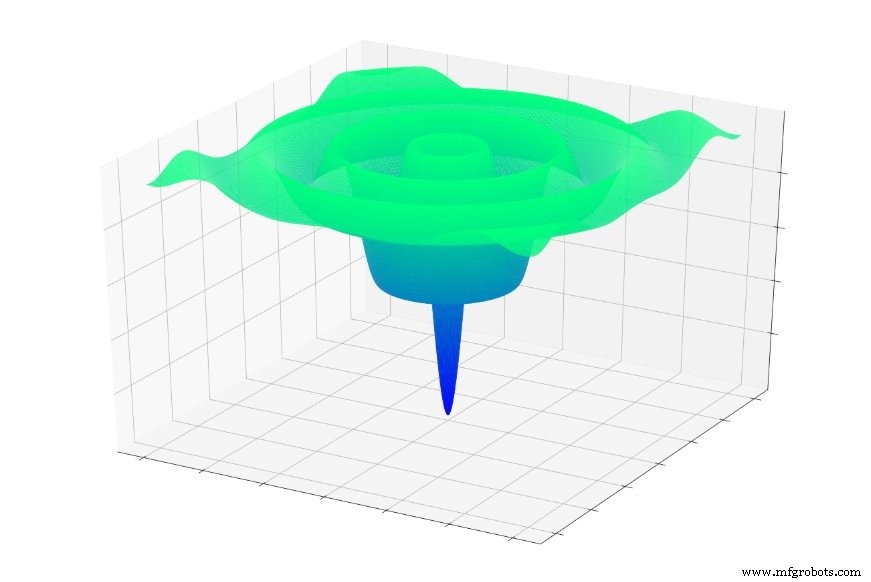
Se você saltasse aleatoriamente para uma dessas funções, muitas vezes escorregaria para um mínimo local. Você estaria no ponto mais baixo de uma parte localizada do gráfico, mas pode não estar nem perto do global mínimo.

A mesma coisa pode acontecer com uma rede neural. A descida do gradiente depende do local informações que, esperamos, conduzam uma rede em direção ao global mínimo. A rede não tem conhecimento prévio sobre as características da superfície de erro geral e, conseqüentemente, quando atinge um ponto que parece ser o fundo da superfície de erro com base em informações locais , ele não pode puxar um mapa topográfico e determinar que precisa voltar para cima a fim de encontrar o ponto que é realmente inferior a todos os outros.

Quando implementamos a descida gradiente básica, estamos dizendo à rede:“Encontre o fundo de uma superfície de erro e permaneça lá”. Não estamos dizendo:“Encontre o fundo de uma superfície de erro, anote suas coordenadas e continue subindo e descendo até encontrar a próxima. Avise-me quando terminar. ”

Queremos realmente encontrar o mínimo global?

É razoável supor que o mínimo global representa a solução ótima e concluir que os mínimos locais são problemáticos porque o treinamento pode “parar” em um mínimo local em vez de continuar em direção ao mínimo global.

Acho que essa suposição é válida em muitos casos, mas pesquisas bastante recentes sobre superfícies de perda de rede neural sugerem que redes de alta complexidade podem realmente se beneficiar de mínimos locais, porque uma rede que encontra o mínimo global terá overtraining e, portanto, será menor eficaz ao processar novas amostras de entrada.

Outro problema que entra em jogo aqui é um recurso de superfície chamado ponto de sela; você pode ver um exemplo no gráfico abaixo. É possível que, no contexto de aplicativos de rede neural reais, os pontos de sela na superfície de erro sejam de fato uma preocupação mais séria do que os mínimos locais.

Conclusão

Espero que você tenha gostado desta discussão sobre os mínimos locais. No próximo artigo, discutiremos algumas técnicas que ajudam uma rede neural a atingir o mínimo global (se de fato é isso que queremos fazer).