O que é análise de malha:procedimento e seus exemplos

No domínio da eletrônica, é mais crucial analisar até mesmo circuitos simples. Para a análise de circuitos simples, princípios como a tensão de Kirchhoff e a lei da corrente de Kirchhoff são usados. Considerando que na situação de circuitos complicados que têm múltiplas fontes de tensão e corrente controladas, deve haver ferramentas adicionais junto com as leis KVL e KCL. Somente com os princípios KVL e KCL, a análise acaba sendo imprecisa e não confiável. Então, para ir com uma análise exata e conhecer as variáveis ​​nesses circuitos, abordagens como malha e nodal devem ser implementadas. Com esses métodos, variáveis ​​como corrente e tensões podem ser conhecidas facilmente. Deixe-nos saber claramente sobre análise de malha, análise de super malha neste artigo.

O que é análise de malha?

A malha é considerada um loop que não possui outros loops dentro do circuito. Aqui, as correntes da malha são usadas como variáveis ​​no lugar das correntes para descobrir toda a análise do circuito. Por isso, a técnica precisa de um número mínimo de equações para ser resolvida. A análise de malha é implementada nos circuitos usando a lei de tensão de Kirchhoff para saber os valores de corrente desconhecidos.

Isso também é denominado como técnica de loop de corrente de malha. Depois disso, os valores de tensão também podem ser conhecidos pela implementação da lei de Ohm. Uma ramificação é considerada como o caminho onde conecta dois nós e é incluída com um elemento de circuito. Quando uma malha consiste em apenas uma ramificação, a corrente da ramificação é denominada corrente da malha. Ao passo que, quando uma malha consiste em dois ramos, a corrente da malha é considerada como a soma ou a diferença dos dois loops da malha quando eles estão em caminhos semelhantes ou opostos.

Etapas

• No conhecimento das variáveis ​​de um circuito, existe um procedimento a ser seguido para a implementação da análise de malhas e os passos podem ser explicados da seguinte forma:
• Na primeira fase, descubra as malhas e marque as correntes da malha no sentido anti-horário ou no sentido horário.
• Observe a quantidade de fluxo de corrente que flui através de cada elemento correspondente às correntes da malha.
• Escreva todas as equações da malha para as malhas observadas. As equações da malha são escritas aplicando a lei de Kirchhoff e depois aplicando a lei de Ohm
• Para descobrir as correntes da malha, resolva as equações da malha observadas conforme a etapa 3.
• Com isso, o fluxo de valores de corrente e tensão em cada elemento do circuito pode ser conhecido pela aplicação de correntes de malha.

Formulário geral para configurar equações na análise de malha

Após a identificação das malhas no circuito, cada uma consiste em uma equação. As equações são o total da queda de tensão em todo o loop da corrente da malha. No caso de circuitos, que possuem mais do que tensão e corrente, a queda de tensão é considerada como a impedância do circuito que é multiplicada pela corrente específica da malha do loop.

Quando a fonte de voltagem existe interna ao loop, então a voltagem presente na fonte pode ser somada ou subtraída com base na condição se é a perda de voltagem ou aumento na voltagem para aquela malha. Mas na condição em que a fonte de corrente não está entre as malhas, a corrente da malha considerará um valor negativo ou positivo da fonte com base na direção da fonte da corrente da malha.

Método de malha atual

Com o circuito abaixo, a análise do método da corrente de malha pode ser conhecida facilmente. No circuito, as correntes de loop I1 e I2 são aplicadas no sentido horário

Dependendo da direção da corrente do loop, as polaridades das quedas de tensão ocorrem nas resistências R1, R2 e R3. Aqui, as correntes I1 e I2 terão caminhos de fluxo de corrente opostos porque o resistor R2 compartilha ambos os loops.

Portanto, ambas as polaridades das tensões podem ser conhecidas. Enquanto nos cenários práticos, R2 pode ser categorizado como duas fases, mas as correntes de loop são especialmente aplicáveis ​​para aplicações de análise. Não há impacto nas polaridades das fontes de tensão porque elas são constantes.

Após a aplicação da lei de tensão de Kirchhoff, as duas equações abaixo podem ser escritas

R2 (I1 - I2) + R1I1 =V1 - Derivado do loop 1

R2 (I2 - I1) + R1I2 =-V2 - Derivado do loop 2

Os termos semelhantes nas equações acima são combinados e, mediante disposição, os mesmos termos aparecem em uma posição semelhante em todas as equações. Quando as correntes de loop são conhecidas, as correntes de ramificação podem ser avaliadas. As equações reorganizadas são:

I1 (R1 + R2) - I2R2 =V1 - For Loop 1

-I1R2 + (R2 - R3) I3 =-V2 - Para Loop 2

Problemas resolvidos de análise de malha

Esta seção mostra os exemplos resolvidos de encontrar corrente em um circuito usando o método de corrente de malha .

No circuito abaixo, descubra a quantidade de tensão que passa pela fonte de corrente de 15 Amps pelo método de análise de malha. Desde que todos sejam fontes atuais

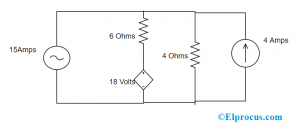
De acordo com o circuito, existe a chance de alterar a fonte de tensão para corrente usando resistência paralela. Para fazer isso, um resistor é colocado em conexão em série com a fonte de tensão e o resistor deve possuir o mesmo valor da fonte de tensão e a tensão é

Vs =IsRs =4 * 4 =16V

Descubra as correntes do ramal (I1 e I2) para os loops e signifique as direções do fluxo da corrente em ambos os loops.

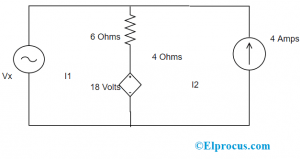
Então, para cada malha (loop), aplique a lei KVL

Malha - 1

Vx - (I1 - I2) - 18 =0

Aqui, I1 =15

Portanto, Vx + (6 * I2) =90

Malha - 2

18 - 6 (I2 - I1) - 4 * I2 - 16 =0

I2 =78/10

=7,8 Amps

De acordo com a equação Mesh-1

Vx =90 - 44,4

Vx =45,6 V

Este é o exemplo resolvido de Resolvendo Duas Malhas usando Análise de Corrente de Malha

Aqui, precisamos descobrir a tensão e as correntes de ramificação. Considere o circuito abaixo.

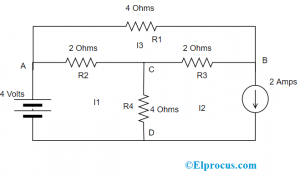
Pela aplicação da lei KVL ao primeiro ciclo, obtemos

V1 - R2 (I1 - I3) - R4 (I1 - I2) =0

4 - 2 (I1) - 2 (I3) - 4 (I1) - 4 (I2) =0

-2 (I3) - 6 (I1) =4

Na aplicação da lei KVL à segunda malha, obtemos

-Vc - R4 (I2 - I1) - R3 (I2 - I3) =0

-Vc =-4 (I1) + 6 (I2) - 2 (I3) =0

Como I2 =-2A, obtemos

-Vc =-4 (I1) -12 - 2 (I3) =0

Na aplicação da lei KVL à terceira malha, obtemos

-R1 (I3) - R3 (I3 - I2) - R2 (I3 - I1) =0

Substituindo I2 =-2A

2 (I1) - 8 (I3) =0

Resolvendo a primeira e a terceira equações da malha, obtemos

I1 =4,46 e I3 =-0,615

Então, Vc =28,61V

E a corrente do ramo é

Iac =I1 - I3

Iac =5,075 amperes

Este é o exemplo resolvido de resolver três malhas usando a análise de corrente de malha

Esses são os exemplos de amostra resolvidos por meio da análise de malha. Uma análise aprofundada deste conceito nos permite resolver circuitos complexos também.

Análise de Super Malha

Para a análise de circuitos enormes e complexos, a análise da supermalha serve como a melhor abordagem do que a análise da malha, pois na supermalha haverá duas malhas compartilhando um componente comum como a fonte de corrente.

A mesma técnica é seguida para análise de circuito de supernodo como uma alternativa para análise de circuito nodal porque este método simplifica esses circuitos complexos fechando o elemento de tensão e minimizando o número de nós de referência para cada fonte de tensão. Na análise da supermalha, a fonte de corrente fica no interior da seção da supermalha, de forma que se possa minimizar as malhas em um para cada fonte de corrente presente.

Quando a fonte de corrente está presente no permissor do circuito, uma única malha pode não ser considerada. Por outro lado, KVL é implementado apenas para aquelas malhas no circuito elétrico modificado.

Vamos considerar um exemplo de análise de supermalha para melhor compreensão.

Usando a análise de supermalha, descubra os valores de V3, i1, i2 e i3 para o circuito abaixo.

Na aplicação de KVL ao Mesh-1, obtemos

10i1 + 80 (i1 - i2) + 30 (i1 - i3) =80

Obtemos 60i1 - 20i2 - 30i3 =80

Pela aplicação da técnica de supermalha à Malha 2 e Malha 3, obtemos

30 =40i3 + 30 (i3 - i1) + 20 (i2 - i1)

70i3 - 50i1 + 20i2 =30

A fonte de corrente individual que está na supermalha corresponde às correntes esperadas da malha que são

15ix =i3 - i2

I3 =15ix + i2

Resolvendo todas as três equações acima, obtemos

i1 =0,58 Amps, i2 =-6,16 Amps e i3 =2,6 Amps

Para encontrar V3, temos v3 =i3 * R3, então

V3 =2,6 * 40 =104V

Usos de análise de malha

O principal uso da análise de malha é para resolver circuitos planares para saber os valores de corrente em qualquer posição nos circuitos elétricos simples e complicados

O outro uso é que cálculos normais para resolver equações são difíceis e mais fórmulas matemáticas são necessárias, enquanto por meio da análise de malha menos cálculos são suficientes.

O outro uso da análise de corrente de malha é uma ponte de pedra de trigo desequilibrada. Para saber isso, considere o exemplo abaixo

Como as proporções dos resistores, R1 / R4 e R2 / R5 não são iguais, podemos entender que haverá algum fluxo de tensão e corrente em R3. Como sabemos que resolver esses tipos de circuitos é complicado pela abordagem da técnica geral de série paralela, precisamos de outra abordagem para resolver isso.

Então, com relação a isso, podemos prosseguir com a aplicação do método da corrente de ramal, mas este método precisa de seis correntes de Ia a If, o que leva a trabalhar em qualquer número de equações. Portanto, essa complexidade pode ser facilmente reduzida através do método de corrente de malha, onde isso requer apenas algumas variáveis.