Dispersão em pequeno ângulo de fractais gordos em nanoescala
Resumo
O espalhamento de pequeno ângulo (de nêutrons, raios-x ou luz; SAS) é considerado para descrever as características estruturais de fractais de gordura em nanoescala determinísticos. Mostramos que no caso de um sistema fractal polidisperso, com igual probabilidade para qualquer orientação, obtém-se as dimensões fractais e os fatores de escala em cada nível estrutural. Isso está de acordo com os resultados gerais deduzidos no contexto da análise de espalhamento de pequeno ângulo de um sistema de nano / micro-fractais orientados aleatoriamente, não interagindo. Aplicamos nossos resultados a um fractal tipo Cantor de gordura bidimensional, calculando expressões analíticas para as intensidades de espalhamento e fatores de estrutura. Explicamos como as propriedades estruturais podem ser calculadas a partir de dados experimentais e mostramos sua correlação com a variação do fator de escala com o número da iteração. O modelo pode ser usado para interpretar dados experimentais SAS registrados na estrutura de fractais de gordura e pode revelar propriedades estruturais de materiais caracterizados por uma lei regular de mudança das dimensões fractais. Ele pode descrever sucessões de decaimentos de lei de potência, com valores decrescentes arbitrários dos expoentes de dispersão, e intercaladas por regiões de intensidade constante.
Introdução
Muitas estruturas hierárquicas geradas em nano e microescala têm características geométricas que são invariáveis sob dilatações de escala, exibindo auto-similaridade e, portanto, tendo propriedades fractais [1, 2]. Embora os avanços recentes na ciência dos materiais e na nanotecnologia permitam a preparação de vários fractais determinísticos em nano / microescala artificiais, com uma autossimilaridade exata [3-7], a grande maioria dos processos naturais geram fractais aleatórios e estatisticamente autossimilares. Uma boa aproximação nos estudos estruturais de formações fractais naturais pode ser feita recorrendo a modelos fractais determinísticos, com a mesma dimensão fractal dos aleatórios. Esta abordagem foi usada com sucesso para mostrar que a transferência através de superfícies fractais aleatórias é muito próxima da resposta de geometrias de modelos determinísticos [8]. Ao introduzir a polidispersidade no algoritmo de construção de um fractal determinístico, podem ser obtidas intensidades de espalhamento de pequeno ângulo (SAS) semelhantes àquelas correspondentes a fractais aleatórios [9]. Além disso, uma abordagem “determinística” é computacionalmente mais eficiente, permitindo a descrição analítica de várias propriedades, como forma fractal, fatores de estrutura e o raio de giração.
Um dos métodos mais confiáveis para determinar as propriedades estruturais de fractais determinísticos e aleatórios [10, 11] é empregar difração de onda no contexto de espalhamento de pequeno ângulo em materiais nano ou microestruturados, usando nêutrons ou ondas eletromagnéticas (x raio, luz, etc.) [12]. É por isso que uma das tarefas fundamentais nas descrições teóricas ligadas às determinações experimentais nesta área de pesquisa é revelar a relação entre a estrutura dos fractais e seu espectro de difração correspondente ou distribuição de intensidade de espalhamento vs. vetor de onda de espalhamento. Muitos estudos experimentais e teóricos foram realizados nesta direção [13-21].
Usando cálculos teóricos padrão e interpolação, o parâmetro que é determinado a partir deste tipo de medidas experimentais é a dimensão fractal de massa D m (consulte o Apêndice 1), com D m
Muitas intensidades de difração experimentais de vários sistemas quimicamente sintetizados e biológicos são caracterizadas, em uma escala logarítmica dupla, por uma sucessão de decaimentos de lei de potência, intercalados por regiões de intensidade constante. Este comportamento pode ser identificado para alguns géis poliméricos [24], glicosídeo hidrolase para substrato de celobiose [25], coacervatos complexos de polieletrólitos [26] ou carbono nanoporoso [27]. Embora o modelo clássico de Beaucage [28] possa fornecer informações estruturais básicas sobre esses sistemas (ou seja, a dimensão da massa ou da superfície fractal e o tamanho geral de cada nível estrutural), uma caracterização mais completa é necessária devido ao grande número de configurações que correspondem a um valor fixo da dimensão fractal. Esta questão foi parcialmente abordada recentemente por Cherny et al. [29] no contexto dos modelos de espalhamento a baixo ângulo (SAS). Foi mostrado que, para fractais de massa determinísticos com uma única escala, podem ser obtidas informações adicionais, como o número da iteração fractal, o número de unidades constituintes básicas e o fator de escala. Além disso, essa abordagem foi usada com sucesso para desenvolver novos modelos para fractais de gordura, se sucessões de decaimentos de power-law estão presentes nas distribuições de espalhamento. Pode ser aplicado a estruturas onde o tamanho total das unidades componentes básicas é da mesma ordem que as distâncias entre elas [30, 31].
O modelo teórico apresentado neste artigo combina modelos anteriores para estender sua aplicabilidade. Ele descreve sucessões de decaimentos de lei de potência, com valores decrescentes arbitrariamente dos expoentes de espalhamento, e intercaladas por regiões de intensidade constante. Nosso modelo também é capaz de fornecer informações mais detalhadas sobre cada nível estrutural do nano / micro-fractal. Para este propósito, consideramos um fractal gordo, representado por um fractal de massa determinística bidimensional com um fator de escala que é dependente do número de iterações, mas com área de superfície não-evanescente no limite de um grande número de iterações, portanto, com um positivo Medida de Lebesgue. Derivamos expressões analíticas da forma fractal e dos fatores de estrutura, e mostramos como determinar as dimensões do fractal e os fatores de escala em cada nível estrutural.
Fundamentos teóricos
Considerando uma matriz de aberturas de difração idênticas, orientadas de forma semelhante, denotadas aqui por Σ , contendo N regiões transparentes, rotuladas por j , um somatório das amplitudes obtidas de cada abertura deve ser levado em consideração. Assim, a distribuição de frequência bem conhecida da amplitude de difração de uma única abertura (Eq. (37) no Apêndice 2) pode ser reescrita como [32]:
$$ A (p, s) =\ sum \ limits_ {j =1} ^ {N} \ iint \ limits _ {- \ infty} ^ {~~~ + \ infty} T (x, y) e ^ {- 2 i \ pi \ left (p (x + x_ {j}) + s (y + y_ {j}) \ right)} \ mathrm {d} x \, \ mathrm {d} y. $$ (1)
As coordenadas de um ponto no quadro local do j a abertura é ( x j , y j ), e T ( x, y ) representa a função de transmissão individual correspondente a cada região transparente. Pode-se trocar somatório por integração porque, em nosso caso, as aberturas são descritas pela mesma função de distribuição individual, de modo que a Eq. (1) pode ser reescrito como:
$$ A (p, s) =\ iint \ limits _ {- \ infty} ^ {~~~ + \ infty} T (x, y) e ^ {- 2 i \ pi (px + sy)} \ mathrm { d} x \, \ mathrm {d} y \ times \ sum \ limits_ {j =1} ^ {N} e ^ {ipx_ {j}} e ^ {isy_ {j}}. $$ (2)
O fator integral da igualdade anterior representa a transformada de Fourier da função de distribuição de cada uma das aberturas idênticas, conforme observado acima. Esta amplitude é modulada pelo fator que contém a soma, representando a transformada de Fourier das distribuições de Dirac-delta da forma \ (A _ {\ delta} ~ =~ \ sum _ {j ~ =~ 1} ^ {N} (x ~ - ~ x_ {j}) (y ~ - ~ y_ {j}) \). Conseqüentemente, a distribuição espacial das aberturas dentro da matriz também é considerada. Portanto, a Eq. (2) pode ser reescrito na forma conhecida como teorema da matriz [32]:
$$ A (p, s) ~ =~ \ mathcal {F} \ left \ {T (x, y) \ right \} \ mathcal {F} \ left \ {A _ {\ delta} \ right \}. $$ (3)
A distribuição de intensidade da imagem difratada no plano de Fourier torna-se:
$$ I (p, s) \ equiv \ left | A (p, s) \ right | ^ {2} =\ left | \ mathcal {F} \ left \ {T (x, y) \ right \} \ right | ^ {2} \ big | \ mathcal {F } \ left \ {A _ {\ delta} \ right \} \ big | ^ {2}. $$ (4)
Como era de se esperar, o primeiro fator no produto corresponde à intensidade de espalhamento de um único orifício, enquanto o segundo revela a forma como esses orifícios estão distribuídos dentro da abertura de difração Σ . Essas quantidades também são conhecidas como fator de forma F ( p, q ) e, respectivamente, o fator de estrutura S ( p, q ) Por isso, os resultados obtidos ao longo do artigo serão expressos usando a seguinte forma de intensidade de espalhamento:
$$ I (p, q) \ equiv F (p, s) S (p, s). $$ (5)
Modelo e método de fractal gordo
O procedimento detalhado para a construção de um fractal Cantor fino (regular) é bem conhecido [33]. Apenas o procedimento de construção principal é resumido aqui. Uma abordagem de cima para baixo é adotada. Começando com um quadrado inicial (ou qualquer outra forma euclidiana) de aresta l 0 (a m =0), cujo centro coincide com a origem do sistema de coordenadas cartesianas e arestas paralelas aos eixos do sistema de coordenadas, qualquer ponto do quadrado satisfaz as condições - l 0 / 2≤ x ≤ l 0 / 2 e - l 0 / 2≤ y ≤ l 0 / 2. Na primeira iteração ( m =1), o quadrado é dividido em quatro outros quadrados, com comprimento de aresta \ (\ beta _ {\ mathrm {s}} ^ {(1)} l_ {0} \). Denotamos com \ (\ beta _ {\ mathrm {s}} ^ {(1)} \ equiv (1- \ gamma _ {1}) / 2 \), com \ (0 <\ beta _ {\ mathrm { s}} ^ {(1)} <1/2 \), o fator de escala da primeira iteração, e com γ 1 a fração do comprimento removido neste ponto, como pode ser visto na Fig. 1 a, b) para m =1. O número colocado entre (⋯), aparecendo como índice superior, quantifica o número da iteração. Não deve ser interpretado como um expoente de uma função de potência. Em termos de fator de escala, as posições dos quatro quadrados são dadas pelos vetores \ (\ boldsymbol {a} _ {j} ~ =~ \ left \ {\ pm \ beta _ {\ mathrm {t}} ^ { (1)} l_ {0}, \ pm \ beta _ {\ mathrm {t}} ^ {(1)} l_ {0} \ right \} \) com todas as combinações de sinais possíveis, onde \ (\ beta _ { \ mathrm {t}} ^ {(1)} ~ =~ \ left (1- \ beta _ {\ mathrm {s}} ^ {(1)} \ right) / 2 \) é usado para simplificar ainda mais as formulações. O quadrado foi escolhido como forma inicial, devido à simplicidade dos cálculos numéricos. Qualquer outra forma geométrica, por exemplo um círculo, pode ser considerada. O efeito da escolha de outra forma é observado apenas na região Porod do fator de forma, o que está além do escopo deste artigo.
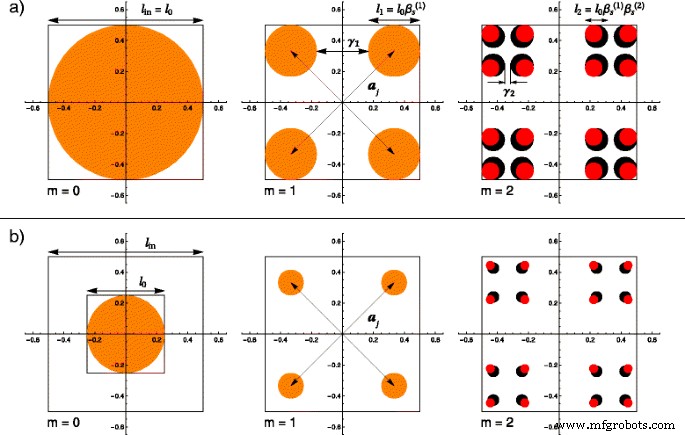
(Cor online) Uma comparação entre fractais regulares e de gordura para as duas primeiras iterações, onde a forma básica em m =0 é um disco de diâmetro l 0 e o tamanho do fractal é l em : a l 0 = l em ; b l 0 = l em / f , com f =2. Em ambos os casos, em m =1 as estruturas coincidem devido a fatores de escala iguais \ (\ beta _ {\ mathrm {s}} ^ {(1)} \). Começando com m =2, o fractal gordo tem um fator de escala maior \ (\ left (\ beta _ {\ mathrm {s}} ^ {(2)}> \ beta _ {\ mathrm {s}} ^ {(1)} \ direita) \) e, portanto, os discos têm um diâmetro maior ( discos pretos ) do que no caso de fractal regular ( discos vermelhos ); a j são os vetores de posição e γ i são as frações do comprimento removido em i a iteração
Os dois primeiros passos descritos acima também são aplicados na construção da versão clássica de um fractal gordo, para iterações m =0 e m =1. É por isso que, até agora, essas duas estruturas coincidem. Para obter o fractal gordo, uma modificação do algoritmo usado na iteração m =1 deve ser feito, escolhendo outro fator de escala em m =2, \ (\ beta _ {\ mathrm {s}} ^ {(2)} \ equiv (1 - \ gamma _ {2}) / 2 \). Aplicando todo o algoritmo no limite de alto número de iterações [34, 35], obtém-se novamente a versão clássica de um fractal gordo. É claro a partir da construção que a versão regular do fractal é recuperada quando os fatores de escala, a cada iteração, são escolhidos para serem iguais \ (\ beta _ {\ mathrm {s}} ^ {(1)} ~ =~ \ beta _ {\ mathrm {s}} ^ {(2)} ~ =~ \ cdots =\ beta _ {\ mathrm {s}} ^ {(m)} \).
Para obter o platô constante entre dois decaimentos de lei de potência no comportamento da intensidade do SAS, devemos levar em consideração que as distâncias entre as unidades de espalhamento são muito maiores do que seu tamanho total. Tal abordagem foi usada inicialmente no contexto de modelos fractais de superfície [36, 37]. Considerando a proporção f da distância total entre as unidades de espalhamento l em e seu tamanho total l 0 , um tem:
$$ f ~ \ equiv ~ l _ {\ text {in}} / l_ {0}. $$ (6)
Para experimentos de espalhamento exibindo platôs de intensidade constante entre duas regiões fractais, valores de f ≫1 deve ser escolhido. No caso de fractais superficiais, aumentando o valor de f leva a um melhor acordo entre a intensidade total do SAS, por um lado, e a aproximação de unidades de espalhamento independentes, por outro [36, 37].
Usando as considerações acima, pode-se descrever as diferenças entre fractais regulares e de gordura. A influência do fator f , apresentado acima, também pode ser visualizado. É por isso que, na Fig. 1, exemplificamos graficamente a comparação usando um disco de raio r 0 ≡ l 0 / 2 = l em / (2 f ) como nossa forma básica. Os resultados das duas primeiras iterações, apresentados em cada linha da Fig. 1, representam as estruturas obtidas para um fractal regular (marcado por discos vermelhos) e um fractal gordo (representado como um disco preto), que também podem ser totalmente sobrepostos ( marcados como discos laranja). Na linha identificada pela Fig. 1 a, o fator f é considerado igual à unidade de forma que as construções clássicas e as formas fractais sejam obtidas. A segunda linha da figura, denotada pela Fig. 1 b, exibe a influência do fator apresentado acima. Nestes cálculos, escolhemos o valor arbitrário de f =2. Observa-se que nas iterações m =0 e m =1, em ambos os casos a e b, as estruturas obtidas dos conjuntos de Cantor regulares e gordos são idênticas e completamente sobrepostas. Isso era esperado devido ao fator de escala comum. No entanto, como pode ser visto no último par de imagens da Fig. 1, começando com m =2, os raios dos discos do fractal gordo são maiores porque seu fator de escala \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) é maior, por definição, do que o regular. Na última imagem da Fig. 2 b, o tamanho dos discos é muito menor do que em sua contraparte da Fig. 2 a devido ao valor não unitário do fator f .
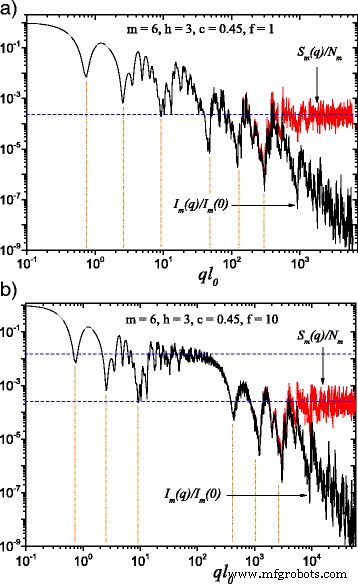
(Cor online) Uma comparação entre a intensidade de espalhamento dada pela Eq. (22) ( curvas pretas ) e fator de estrutura dado pela Eq. (24) ( curvas vermelhas ) em m =6 e a média das orientações de acordo com a Eq. (25). Aqui, h =3 (ou seja, o fator de escala é mantido constante por três iterações consecutivas), enquanto a forma básica no cálculo da intensidade de espalhamento é um quadrado do tamanho da borda l 0 : a l 0 = l em ; b l 0 = l em / f (com f =10). Quando f ≠ 1, um platô de intensidade constante aparece entre os dois decaimentos generalizados da lei de potência (Fig. 2 b). Linhas horizontais denotam a assíntota do fator de estrutura ≃1 / N m , enquanto as posições mínimas são estimadas de acordo com a Eq. (26)
Para obter as próprias leis de potência, é necessário generalizar ainda mais o modelo clássico do fractal gordo. Isso é feito considerando que as mudanças do fator de escala não são feitas com cada iteração, mas a cada segundo, terceiro, ⋯, ou, de modo geral, a cada h a iteração. A fração de comprimentos removidos no m a iteração é:
$$ \ gamma_ {m} ~ =~ c ^ {p_ {m}}, $$ (7)
com 0 < c <1. A função p m é definido como:
$$ p_ {m} \ equiv \ left \ lfloor 1+ \ frac {m-1} {h} \ right \ rfloor, $$ (8)
para qualquer valor inteiro positivo de m , com h =1, ⋯, m , onde a função floor ⌊ ⋯ ⌋ foi usada. Assim, o fator de escala correspondente ao m a iteração é dada por:
$$ \ beta _ {\ mathrm {s}} ^ {(m)} ~ =~ \ frac {1- \ gamma_ {m}} {2}. $$ (9)
Está claro agora que o propósito da função p m é manter o fator de escala constante para h iterações ( h < m )
Os componentes dos vetores de posição de cada quadrado podem ser escritos como:
$$ \ beta _ {\ mathrm {t}} ^ {(m)} =\ frac {\ beta _ {\ mathrm {s}} ^ {(m)}} {2} + \ frac {\ gamma_ {m}} {2}, $$ (10)
enquanto o comprimento da borda de cada quadrado é dado por:
$$ l_ {m} =\ frac {l_ {0}} {2 ^ {m}} \ prod_ {i =1} ^ {m} (1- \ gamma_ {i}). $$ (11)
O fator f deve ser usado na fórmula do comprimento l 0 levar em consideração que, para iterações entre ( h +1) th e m th, o tamanho dos quadrados diminui em relação às distâncias entre eles:
$$ l_ {0} =\ left \ {\ begin {array} {ll} l _ {\ text {in}}, &\ mathrm {for ~~ iterations ~~} \ leq h \\ l _ {\ text {in }} / f, &\ mathrm {para ~~ iterações ~~}> h, \ end {array} \ right. $$ (12)
onde h < m . O número de quadrados em cada iteração é:
$$ N_ {m} ~ =~ 4 ^ {m}. $$ (13)
Assim, a cada escala, considerada como iteração com fator de escala constante, tem-se uma dimensão fractal diferente dada por [29, 38, 39]:
$$ D _ {\ mathrm {m}} ~ =~ - \ frac {2 \ ln 2} {\ ln \ beta _ {\ mathrm {s}} ^ {(m)}}. $$ (14)
No limite de um grande número de iterações, a dimensão fractal do conjunto fractal construído será [34]:
$$ D \ equiv \ lim \ limits_ {m \ rightarrow \ infty} {\ frac {\ ln N_ {m}} {\ ln (l_ {0} / l_ {m})}} =2, $$ (15 )
que é o valor esperado para um fractal de gordura bidimensional. Finalmente, se um i é a área relativa removida em i a iteração, então \ (\ prod _ {i =1} ^ {m} (1-a_ {i})> 0 \) se \ (\ sum _ {i =1} ^ {\ infty} a_ {i} <\ infty \) e, portanto, o modelo satisfaz a definição e as características dos fractais de gordura [35].
Resultados e discussão
De acordo com o princípio de Babinet, podemos concluir que em m Na iteração, as aberturas na grade são os quadrados restantes no fractal, enquanto as partes removidas tornam-se opacas à radiação.
Intensidade de espalhamento monodispersa e fator de estrutura
A fim de derivar a expressão analítica da intensidade de espalhamento para o fractal Cantor de gordura, começamos escrevendo a relação de recorrência da transmissão de grade para uma iteração arbitrária correspondente a 1 D caso. Em m =0, temos
$$ T_ {0} (l_ {0}, x) \ equiv \ text {rect} (l_ {0}, x) =\ left \ {\ begin {array} {ll} 1, &| x |
$$ \ begin {alinhados} T_ {1} (l_ {1}, x,) =T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x-l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right) + \\ T_ {0} (l_ {1}, x) \ ast \ delta \ left (\ frac {x + l_ {0} \ beta _ {\ mathrm {t}} ^ {(1)}} {l_ {1}} \ right), ~~~~~~~~~~~~~ \ end {alinhado} $$ (17)
onde δ ( x - a ) é a distribuição Dirac-delta unidimensional em x = a . O símbolo ∗ representa o operador de convolução. Portanto, em m a iteração, podemos escrever:
$$ \ begin {alinhado} T_ {m} (l_ {m}, x) =T_ {m-1} (l_ {m}, x) \ ast \ delta \ left (\ frac {x-u_ {m} } {l_ {m}} \ right) + \\ T_ {m-1} (l_ {m}, x, y) \ ast \ delta \ left (\ frac {x + u_ {m}} {l_ {m }} \ right), ~~~~~~~~~~~~ \ end {alinhado} $$ (18)
onde \ (u_ {m} ~ =~ l_ {0} \ beta _ {\ mathrm {t}} ^ {(m)} \ prod _ {j =1} ^ {m-1} \ beta _ {\ mathrm {s}} ^ {(j)} \). Executando uma transformada de Fourier na Eq. (18), verifica-se que a amplitude espalhada em m a iteração é:
$$ A_ {m} (p) =2 ^ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ prod \ limits_ {i =1} ^ { m} \ cos (2 \ pi p u_ {i}). $$ (19)
Desde o 2 D modelo de fractal gordo é um produto direto de dois fractais de gordura unidimensionais, sua transformada de Fourier pode ser escrita como um produto de duas transformadas de Fourier unidimensionais. Portanto, a amplitude de espalhamento bidimensional pode ser escrita como:
$$ A_ {m} (p, s) \ equiv A_ {m} (p) A_ {m} (s), $$ (20)
e assim,
$$ \ begin {alinhados} A_ {m} (p, s) =N_ {m} \ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ {m})} {\ pi s l_ {m}} \ times \\ \ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}), \ end {alinhado} $$ (21)
de modo que a intensidade de espalhamento se torna:
$$ \ begin {alinhados} I_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin ( \ pi s l_ {m})} {\ pi s l_ {m}} \ right) ^ {2} \ times \\ N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ right) ^ {2}. \ end {alinhado} $$ (22)
O primeiro fator na equação anterior, representando a intensidade de difração devido ao fator de forma, conforme declarado na Eq. (5):
$$ F_ {m} (p, s) =\ left (\ frac {\ sin (\ pi p l_ {m})} {\ pi p l_ {m}} \ frac {\ sin (\ pi s l_ { m})} {\ pi s l_ {m}} \ right) ^ {2}, $$ (23)
corresponde à intensidade de espalhamento obtida a partir de um único quadrado da aresta l m . O segundo fator, representando a intensidade de difração devido ao fator de estrutura, conforme declarado na Eq. (5):
$$ S_ {m} (p, s) =N_ {m} ^ {2} \ left (\ prod \ limits_ {i =1} ^ {m} \ cos (2 \ pi p u_ {i}) \ cos (2 \ pi s u_ {i}) \ direita) ^ {2}, $$ (24)
descreve a forma como os quadrados são distribuídos. A intensidade total da radiação espalhada é o produto de F m ( p, s ) e S m ( p, s )
A decadência de força-lei da intensidade, conforme formulado na Eq. (22), é obtido após realizar a média de todas as orientações [29]. Considerando a probabilidade igual para qualquer orientação, a média pode ser calculada no caso de fractais bidimensionais integrando em todas as direções do vetor de espalhamento q =( p, s ):
$$ \ langle f (p, s) \ rangle =\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} f (q, \ phi) \ mathrm {d} \ phi, $ $ (25)
onde p = q cos ϕ e s = q pecado ϕ . Assim, a intensidade de espalhamento I ( q ) é obtido em função do módulo de transferência de momento q ≡ | q |
Porque, a partir da definição do fator de estrutura, tem-se \ (S_ {m} (0) ~ =~ N_ {m} ^ {2} \), onde N m é o número de quadrados, conforme definido na Eq. (13), o procedimento padrão de normalização S m (0) =1 pode ser adotado, conforme descrito em [11, 29].
Os resultados calculados para a intensidade de espalhamento monodisperso I m ( q ) e fator de estrutura S m ( q ), com m =6, são exibidos na Fig. 2 para o fractal de gordura clássico ( f =1 na Fig. 2 a) e, para o modelo de fractal estendido desenvolvido neste trabalho ( f =10 na Fig. 2 b). Para obter a Fig. 2 b, consideramos h =3 para que o fator de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) das três primeiras iterações fosse mantido constante, então ele tinha um outro valor constante \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) para as próximas três iterações. Como esperado, em ambos os casos (para f =1 e f =10), as diferenças entre a intensidade de espalhamento, por um lado, e o fator de estrutura, por outro, podem ser observadas quando \ (q \ gtrsim 1 / l_ {m} \). Nesta região, a intensidade de espalhamento tem uma decadência de lei de potência I ( q ) ∝ q −3 . O fator de estrutura tem um valor assintótico que tende a 1 / N m , representado pela linha horizontal na Fig. 2 a ou pela linha horizontal inferior na Fig. 2 b [29, 33].
Uma sucessão de dois decaimentos generalizados da lei de potência, identificáveis como uma superposição de máximos e mínimos, sobre um decaimento simples de lei de potência, pode ser vista na Fig. 2 a. Mas na Fig. 2 b, uma região de intensidade aproximadamente constante, no domínio 20≲ ql 0 ≲100, pode ser claramente distinguido, englobado pelos dois decaimentos sucessivos da lei de potência generalizada. Isso se deve à diminuição do tamanho dos quadrados em uma ordem de magnitude ( f =10) em comparação com as distâncias entre eles. Esta região, observável em torno da linha horizontal superior na Fig. 2 b tem a assíntota 1 / N 3 , o mesmo do fator de estrutura do fractal de gordura clássico, apresentando um comportamento semelhante ao caso de considerar apenas as três primeiras iterações.
Além disso, pode-se observar na Figura 2 que o número de mínimos em cada escala coincide com o número de iterações do fator de escala constante. Esses mínimos ocorrem quando a radiação que passa por diferentes quadrados dentro do fractal interfere e estão em oposição de fase e, portanto, as distâncias mais freqüentemente encontradas entre o centro dos quadrados (2 u m ) são iguais a π / q . É por isso que as posições aproximadas dos mínimos são obtidas a partir da relação:
$$ q_ {i} \ simeq \ frac {\ pi} {2 u_ {i}}, ~~~~ i =1, \ cdots, m $$ (26)
indicado na Fig. 2 por linhas verticais. Para as primeiras seis iterações, observa-se uma concordância bastante boa entre as posições calculadas usando a Eq. (26), e aqueles encontrados na intensidade de espalhamento, ou fator de estrutura. Essa aproximação pode ser menos precisa para iterações mais altas, uma vez que o número da iteração aumenta acima de um certo valor porque, nesses casos, mais e mais distâncias são comparáveis àquela encontrada com mais frequência. No entanto, esta aproximação deve funcionar muito bem na prática, onde dificilmente se pode esperar distinguir mais do que quatro ou cinco mínimos.
Para cada escala individual, em um determinado intervalo 1 / (2 u i ) ≲ q ≲1 / (2 u i +1 ), o padrão de difração é produzido pela interferência de apenas o i iteração fractal. Isso pode ser usado para mostrar que, dentro deste intervalo, as funções I m ( q ) q D e S m ( q ) q D são log-periódicos [29], onde D é a dimensão fractal correspondente a uma determinada escala. Em particular, para os resultados mostrados nas Figs. 2 e 3, as funções I m ( q ) q -1.1 e S m ( q ) q -1.1 são log-periódicos com o ponto final \ (1 / \ beta _ {\ mathrm {s}} ^ {(1)} \) para as três primeiras iterações, enquanto I m ( q ) q -1,51 e S m ( q ) q -1,51 são log-periódicos com \ (1 / \ beta _ {\ mathrm {s}} ^ {(2)} \) para o segundo grupo de três iterações.
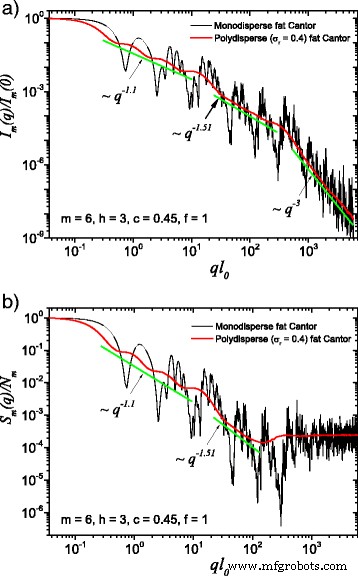
(Cor online) Uma comparação entre sistemas monodispersos e polidispersos: a intensidade de espalhamento (Eq. (22)); b fator de estrutura (Eq. (24)), calculado sobre todas as orientações do fractal, de acordo com a Eq. (25). Aqui, f =1, m =6, h =3 (ou seja, o fator de escala é mantido constante por três iterações consecutivas), e a forma básica é um quadrado do comprimento da aresta inicial l 0 = l em . Para ambos os casos, a polidispersidade mancha as curvas de espalhamento monodispersas e as dimensões fractais podem ser recuperadas em cada nível estrutural
De maneira semelhante aos fractais de massa determinísticos, Eq. (26) pode ser usado para obter vários parâmetros estruturais que caracterizam os fractais de gordura. Primeiro, o número total de mínimos coincide com o número total de iterações fractais. A Figura 2 mostra que o fractal consiste em três iterações com fator de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) e três iterações com fator de escala \ (\ beta _ {\ mathrm {s} } ^ {(2)} \). Em segundo lugar, a partir da periodicidade desses mínimos (ou da periodicidade de I m ( q ) q D e S m ( q ) q D ), os fatores de escala podem ser recuperados. Na Fig. 2 b, o fator de escala \ (\ beta _ {\ mathrm {s}} ^ {(1)} \) pode ser obtido a partir da periodicidade dos mínimos em ql 0 ≃7,25 e 90, enquanto o fator de escala \ (\ beta _ {\ mathrm {s}} ^ {(2)} \) pode ser obtido a partir da periodicidade dos mínimos em ql 0 ≃400,1000 e 2500. Além disso, o comprimento do platô intermediário entre as regiões fractais pode ser usado como uma indicação da razão ( f ) de distâncias entre unidades de espalhamento e seu tamanho geral. Na Fig. 2b, este intervalo corresponde a 13≲ ql 0 ≲130.
Intensidade de dispersão polidispersa e fator de estrutura
Nesta parte do nosso trabalho, podemos considerar agora que os tamanhos das grades obedecem a uma função de distribuição D N ( l 0 ), definido de tal forma que D N ( l 0 ) d l 0 dá a probabilidade do tamanho da grade fractal estar no intervalo ( l 0 , l 0 + d l 0 ) Esta etapa introduz a polidispersidade em nosso modelo de fractal gordo. Nós exemplificamos isso escolhendo uma distribuição log-normal:
$$ D _ {\ mathrm {N}} (l_ {0}) =\ frac {1} {\ sigma l_ {0} (2 \ pi) ^ {1/2}} e ^ {- \ frac {\ left (\ log (l_ {0} / \ mu) + \ sigma ^ {2} / 2 \ direita) ^ {2}} {2 \ sigma ^ {2}}}, $$ (27)
com variação relativa \ (\ sigma _ {\ mathrm {r}} =\ left (\ left \ langle l_ {0} ^ {2} \ right \ rangle _ {D} - \ mu ^ {2} \ right) ^ {1/2} / \ mu \), valor médio μ =〈 l 0 〉 D , e variância \ (\ sigma =\ left (\ log \ left (1+ \ sigma _ {\ mathrm {r}} ^ {2} \ right) \ right) ^ {1/2} \). Usando Eqs. (21) and (27) one obtains the polydisperse intensity averaged over the distribution function:
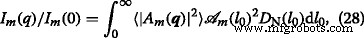
Onde
 is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term
is the corresponding area at m th iteration. The structure factor is calculated in a similar manner, but without the term  [29].
[29]. The computed results in the case of polydisperse (red curves) and monodisperse (black curves) scattering intensities (labeled by a) and structure factors (labeled by b) can be seen in Figs. 3 and 4. The difference between them is given by the value of the f factor. In Fig. 3, the classical construction of a fat fractal was used so that f =1, while taking into account the smaller sizes of the basic units leads to the choice of f =10 in Fig. 4. Polydispersity is calculated for a relative variance of σ r =0.4. It can be seen that the oscillations are smeared out, the overall amplitude decreases, so that the scattering curves become smoother [29, 40]. However, for this particular value of σ r , the positions of main minima and maxima are still observable.
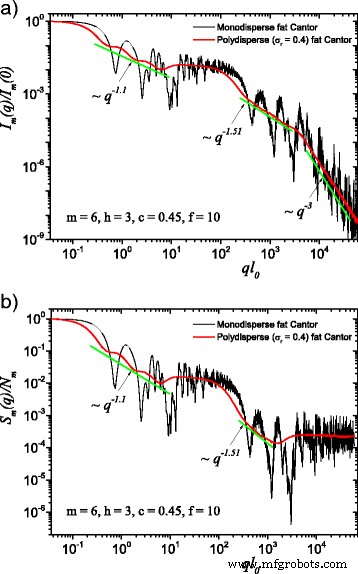
(Color online) A comparison between monodisperse and polydisperse systems:a scattering intensity (Eq. (22)); b structure factor (Eq. (24)), averaged over all orientations of the fractal, according to Eq. (25). Here, f =10 (and thus, a region of constant intensity appears at about 20≲ql 0 ≲100), m =6, h =3 (i.e., the scaling factor is kept constant for three consecutive iterations), and the basic shape is a square of initial edge length l 0 =l in . For both cases, the polydispersity smears out monodisperse scattering curves, and the fractal dimensions can be recovered at each structural level
More generally, for small values of σ r (i.e., small enough that the oscillations are observable), the estimation given by Eq. (26) can be still used. Hence, the number of fractal iterations, the scaling factor at each structural level, the ratio of the distances between scattering units, and their overall size can be recovered. When σ r is increased to high enough values so that oscillations are completely smeared out, the scattering curves become simple power-law decays. Since we used a narrow bell-shaped distribution, the scattering exponent is preserved. Moreover, it gives, for each power-law decay, the fractal dimension of that particular structural level. This is in good agreement with the theoretical estimation of Eq. (14). This is also in accordance with experimental setups, where almost every scattering curve has a certain degree of polydispersity. Thus, our developed fat fractal model, with an interleaved region of constant intensity, recovers the fractal dimension at each structural level from polydisperse experimental data.
Conclusions
In this article, we suggest a theoretical model that generalizes the standard one for nanoscale fat fractals. It is characterized by the fact that the initial edge size of the elementary unit shape is taken to be much smaller than that of the overall size of the fractal, and thus, much smaller than the distances between the elementary units inside the fractal. Figure 1 b illustrates the basic model, when a quotient of 1/2 is considered in-between these quantities, respectively.
Based on this model, an analytical formula is calculated and presented, in Eq. (22) for the scattering intensity and in Eq. (24) for the structure factor. Averaging over all possible orientations is done according to Eq. (25). These averaged quantities are characterized, on a double logarithmic scale, by the presence of two structural levels, and thus by two power-law decays interleaved by a region of constant intensity, represented by a plateau, as seen in Figs. 2 b and 4. This plateau coincides with the asymptotic region of the structure factor of the fat fractal, as if we would have considered only the contribution from the first structural level, when the scaling factor was kept constant. The asymptotic values of the plateaus can be used to obtain the number of scattering units for each structural level. The length of the plateau is controlled by the value of f . The power-law decays encompassing the plateau are obtained by keeping constant the scaling factors for a finite number of iterations, in our case, as an example, for three out of a total of six. The slope of the second power-law decay is higher because the values of scaling factors, by definition, increase at each structural level, and this is confirmed by our numerical computations, as can be seen in Figs. 2, 3, and 4.
We also described the polydisperse case of the fat fractal model. Here, the sizes of the composing units obey, as an example, a log-normal distribution function. We obtained smoothed curves for the scattering intensities and structure factors. The monodisperse scattering curves as well as the polydisperse ones, with small enough values of the relative variance, allow to obtain the scaling factors at each structural level, while the scattering exponents in the polydisperse curve give the fractal dimensions at each structural level. The chosen value of 0.4 for the relative variance is meant to illustrate the case in which one can still observe some minima in the scattering characteristics, and the curves still retain a shape close to power-law decays.
The results obtained in the framework of the suggested model can be used to reveal structural properties of fractal materials characterized by a regular law of changing of the fractal dimensions. The proposed model is also a very versatile one because it can be extended to include other features such as different shapes of the elementary unit, more than two structural levels, or it can be adapted to work in other Euclidean dimensions. These results are useful for a detailed description of experimental diffraction data in the context of small-angle scattering obtained from various complex nano- and micro- scaled hierarchical structures.
Appendix
fractal dimension
Mass and, respectively, surface fractal dimensions are probably the most important quantities that characterize a fractal. Actually, we will deal only with deterministic mass fractals, and we shall refer to mass fractal dimension, simply as the fractal dimension (D m )
In general terms, the mass-radius relation can be rewritten as [2]:
$$ M(r) =A(r) r^{D_{\mathrm{m}}}, $$ (29)
where the scaling law correction A (r ) tends to a constant value if r →∞ .
If it is known a priori that the structure is a fractal in the high number limit, the fractal dimension can be found straight from the first iteration. To illustrate this procedure, let us consider a fractal of size l 0 , composed of k elementary units at the first iteration, each of size β s l 0 , where β s is a scaling factor. Since the mass-radius relation, given by Eq. (29), is equivalent with the scale-invariance relation [2]:
$$ M(\beta_{\mathrm{s}}l_{0}) =\beta_{\mathrm{s}}^{D_{\mathrm{m}}}M(l_{0}), $$ (30)
one can write M (l 0 )=kM (β s l 0 ) Using Eq. (29), one obtains a direct method to compute the fractal dimension, via:
$$ k \beta_{\mathrm{s}}^{D_{\mathrm{m}}} =1. $$ (31)
fraunhofer diffraction and the array theorem
Let us consider a two-dimensional diffracting aperture Σ , laid in the (x,y ) plane, illuminated in the positive z direction. In an observation plane (u,v ), parallel to Σ , the complex-valued amplitude of the obtained diffraction image, computed using the framework of scalar theory of diffraction, according to the Huygens-Fresnel principle, can be written as [41]:
$$ A(u,v) =\frac{z}{i\lambda} \iint\limits_{\Sigma} A(x,y)\frac{e^{ikr}}{r^{2}} \mathrm{d} x\,\mathrm{d} y. $$ (32)
In the previous formula, \(r =\sqrt {z^{2}+(u-x)^{2}+(v-y)^{2}}\) is the distance between two arbitrarily points taken, respectively, from the plane containing Σ and from the observation plane. For the Fraunhofer diffraction model to be applicable, this distance must satisfy the condition of being much bigger than the wavelength λ .
Performing a binomial expansion of the square root in Eq. (32) and retaining only the first two terms, one obtains [41]:
$$ r \approx z\left(1 + \frac{(u-x)^{2}}{2z^{2}} + \frac{(v-y)^{2}}{2z^{2}}\right). $$ (33)
This approximation leads to the Fresnel diffraction integral:
$$ \frac{A(u,v)}{P(u,v)} =\iint\limits_{-\infty}^{~~~+\infty} \left\{A(x,y) e^{i\frac{k}{2z}(x^{2} + y^{2})}\right\} e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y, $$ (34)
where the prefactor P (u,v ) is given by
$$ P(u,v) =\frac{e^{ikz}e^{i\frac{k}{2z}(u^{2}+v^{2})}}{i\lambda z}, $$ (35)
and k =2π /λ . Considering, in addition, that the condition z ≫k Max(x 2 +y 2 )/2 is satisfied, one has \(\text {Exp}{\left (\frac {k}{2z}(x^{2}+y^{2})\right)} \simeq 1\). Rewriting Eq. (34), the Fraunhofer approximation becomes:
$$ A(u,v) =P(u,v)\iint\limits_{-\infty}^{~~~+\infty} A(x,y) e^{-i \frac{2\pi}{\lambda z}(ux + vy)}\mathrm{d}x\,\mathrm{d}y. $$ (36)
Denoting the spatial frequencies with p =u /(λ z ) and s =v /(λ z ) and ignoring the multiplicative phase factor P (u,v ) preceding the integral in Eq. (36), the amplitude becomes simply the Fourier transform of the distribution of the Σ aperture. Considering that the illumination is made using a monochromatic, unit-amplitude plane-wave, at normal incidence, and that the field distribution across the aperture is equal to its transmission function T (x,y ), one obtains the frequency distribution of the diffraction amplitude in the phase space:
$$ A(p,s) =\iint\limits_{-\infty}^{~~~+\infty} T(x,y) e^{-2 i \pi (px + sy)}\mathrm{d}x\,\mathrm{d}y. $$ (37)
Nanomateriais
- Conversão de numeração decimal
- De elétrico para eletrônico
- Substituto de gordura
- 3 razões para fazer a transição de C para C ++
- Cientistas da IBM inventam um termômetro para nanoescala
- O próximo jato de óleo grande está em nanoescala
- Nanocelulose de algas azuis
- Não condutores conduzem corrente em nanoescala
- Preparação de Nanorods de Alumina a partir de Lodo de Alumina Contendo Cromo
- Da IU à IA:uma jornada de automação



