Conversões Δ-Y e Y-Δ

Em muitas aplicações de circuito, encontramos componentes conectados em uma das duas maneiras de formar uma rede de três terminais:a configuração "Delta" ou Δ (também conhecida como "Pi" ou π) e a configuração "Y" ( também conhecida como configuração “T”).



É possível calcular os valores adequados dos resistores necessários para formar um tipo de rede (Δ ou Y) que se comporta de forma idêntica ao outro tipo, conforme analisado apenas a partir das conexões dos terminais. Ou seja, se tivéssemos duas redes de resistores separadas, uma Δ e uma Y, cada uma com seus resistores ocultos, com nada além dos três terminais (A, B e C) expostos para teste, os resistores poderiam ser dimensionados para o duas redes, de modo que não haveria como determinar eletricamente uma rede separada da outra. Em outras palavras, redes Δ e Y equivalentes se comportam de forma idêntica.

Equações de conversão Δ e Y

Existem várias equações usadas para converter uma rede para a outra:



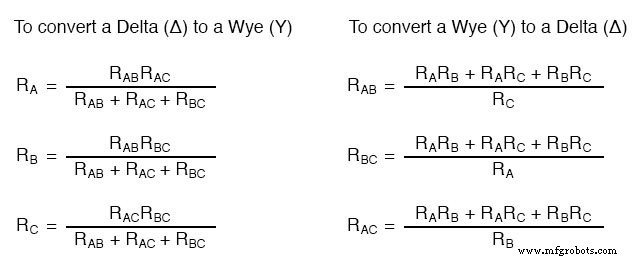
As redes Δ e Y são vistas com frequência em sistemas de energia CA trifásicos (um tópico abordado no volume II desta série de livros), mas mesmo assim são geralmente redes balanceadas (todos os resistores iguais em valor) e conversão de um para o outro não precisa envolver tais cálculos complexos. Quando o técnico médio precisaria usar essas equações?

Aplicação da conversão Δ e Y

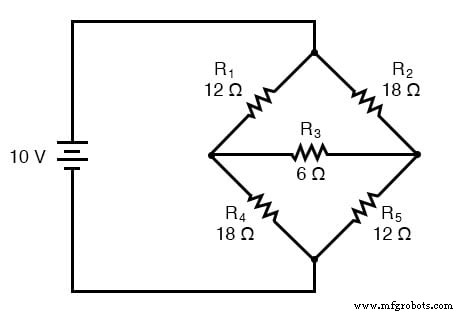
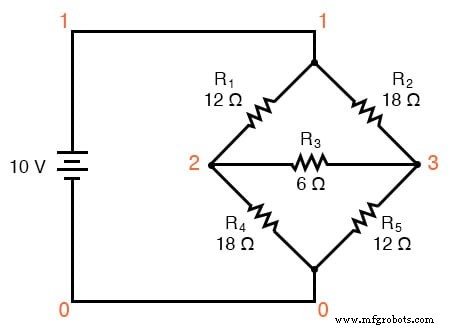
Uma aplicação principal para a conversão Δ-Y está na solução de circuitos de ponte desequilibrada, como a que se segue:



A solução deste circuito com análise de Corrente de Ramificação ou Corrente de Malha está bastante envolvida, e nem os Teoremas de Millman nem de Superposição são de alguma ajuda, uma vez que há apenas uma fonte de energia. Poderíamos usar o teorema de Thevenin ou Norton, tratando R ₃ como nossa carga, mas que diversão seria?

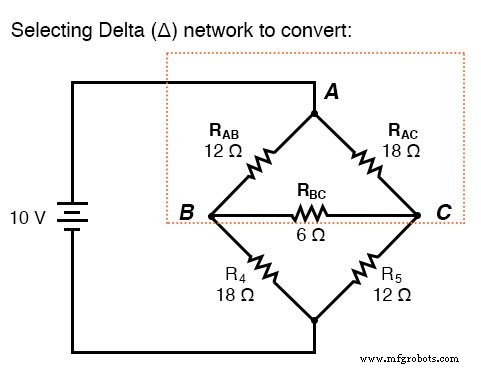
Se tratássemos os resistores R ₁ , R ₂ e R ₃ como sendo conectado em uma configuração Δ (R _ab , R _ac e R _bc , respectivamente) e gerar uma rede Y equivalente para substituí-los, poderíamos transformar este circuito de ponte em um circuito de combinação série / paralelo (mais simples):



Após a conversão Δ-Y. . .



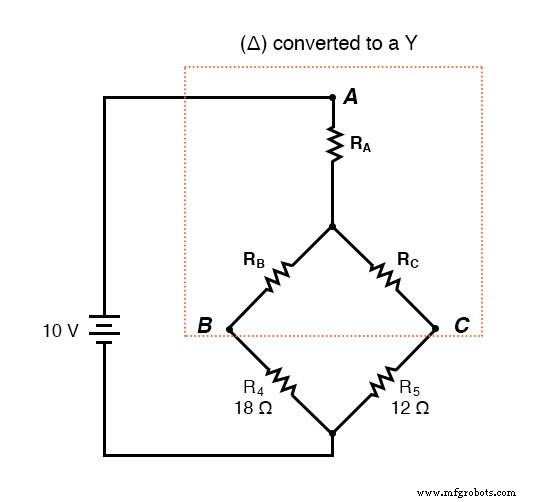
Se realizarmos nossos cálculos corretamente, as tensões entre os pontos A, B e C serão as mesmas no circuito convertido e no circuito original, e podemos transferir esses valores de volta para a configuração original da ponte.





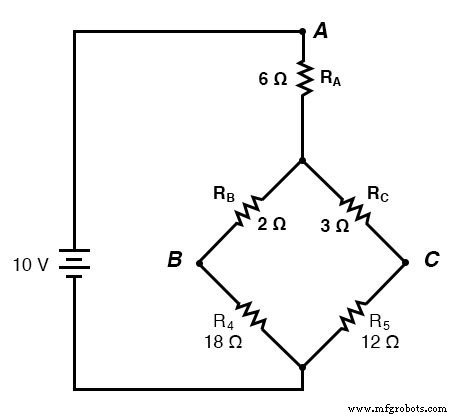
Resistores R ₄ e R ₅ , é claro, permanecem os mesmos em 18 Ω e 12 Ω, respectivamente. Analisando o circuito agora como uma combinação série / paralelo, chegamos às seguintes figuras:



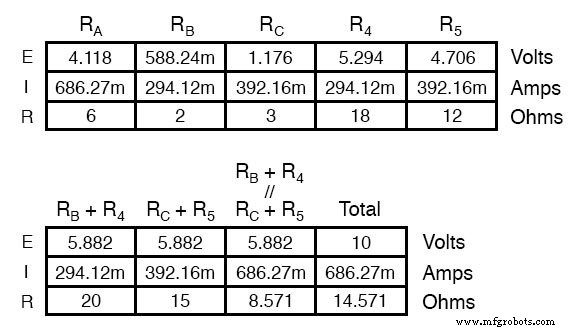
Devemos usar os valores das quedas de tensão da tabela acima para determinar as tensões entre os pontos A, B e C, vendo como elas se somam (ou subtraem, como é o caso com a tensão entre os pontos B e C):





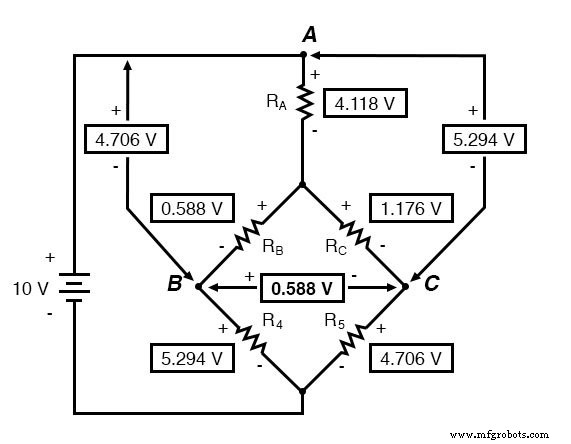
Agora que conhecemos essas tensões, podemos transferi-las para os mesmos pontos A, B e C no circuito de ponte original:



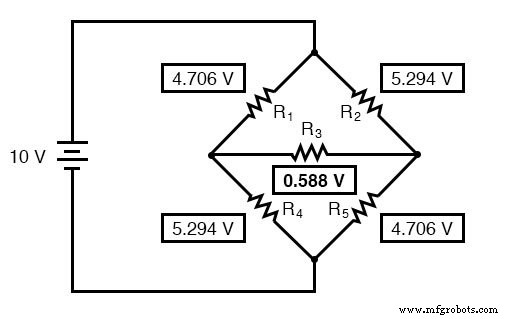
A tensão cai em R ₄ e R ₅ , é claro, são exatamente os mesmos que eram no circuito conversor.

Neste ponto, poderíamos tomar essas tensões e determinar as correntes do resistor através do uso repetido da Lei de Ohm (I =E / R):

Simulação com SPICE

Uma simulação rápida com SPICE servirá para verificar nosso trabalho:

 circuito de ponte não balanceada v1 1 0 r1 1 2 12 r2 1 3 18 r3 2 3 6 r4 2 0 18 r5 3 0 12 .dc v1 10 10 1 .print dc v (1,2) v (1,3) v (2,3) v (2,0) v (3,0) .fim v1 v (1,2) v (1,3) v (2,3) v (2) v (3) 1,000E + 01 4,706E + 00 5,294E + 00 5,882E-01 5,294E + 00 4,706E + 00 

Os valores de tensão, lidos da esquerda para a direita, representam quedas de tensão nos cinco respectivos resistores, R ₁ até R ₅ . Eu poderia ter mostrado as correntes também, mas como isso exigiria a inserção de fontes de tensão "fictícias" na netlist do SPICE, e como estamos principalmente interessados ​​em validar as equações de conversão Δ-Y e não a Lei de Ohm, isso será suficiente.

REVER:

• As redes “Delta” (Δ) também são conhecidas como redes “Pi” (π).
• As redes “Y” também são conhecidas como redes “T”.
• As redes Δ e Y podem ser convertidas em suas contrapartes equivalentes com as equações de resistência adequadas. Por "equivalente", quero dizer que as duas redes serão eletricamente idênticas conforme medido a partir dos três terminais (A, B e C).
• Um circuito de ponte pode ser simplificado em um circuito em série / paralelo convertendo metade dele de uma rede Δ em uma rede Y. Depois que as quedas de tensão entre os três pontos de conexão originais (A, B e C) forem resolvidas, essas tensões podem ser transferidas de volta para o circuito de ponte original, através desses mesmos pontos equivalentes.

PLANILHA RELACIONADA:

• Planilha de circuitos trifásicos Delta e Wye