MATLAB - Operadores

Um operador é um símbolo que diz ao compilador para realizar manipulações matemáticas ou lógicas específicas. O MATLAB foi projetado para operar principalmente em matrizes e arrays inteiros. Portanto, os operadores no MATLAB funcionam tanto em dados escalares quanto não escalares. O MATLAB permite os seguintes tipos de operações elementares -

• Operadores aritméticos
• Operadores Relacionais
• Operadores lógicos
• Operações bit a bit
• Definir operações

Operadores aritméticos

O MATLAB permite dois tipos diferentes de operações aritméticas -

• Operações aritméticas matriciais
• Operações aritméticas de matriz

As operações aritméticas matriciais são as mesmas definidas na álgebra linear. As operações de array são executadas elemento por elemento, tanto em array unidimensional quanto multidimensional.

Os operadores de matriz e operadores de matriz são diferenciados pelo símbolo de ponto (.). No entanto, como a operação de adição e subtração é a mesma para matrizes e arrays, o operador é o mesmo para ambos os casos. A tabela a seguir fornece uma breve descrição dos operadores -

Mostrar exemplos

Nº Sr.	Operador e Descrição
1	+ Adição ou mais unário. A+B soma os valores armazenados nas variáveis ​​A e B. A e B devem ter o mesmo tamanho, a menos que uma seja escalar. Um escalar pode ser adicionado a uma matriz de qualquer tamanho.
2	- Subtração ou menos unário. A-B subtrai o valor de B de A. A e B devem ter o mesmo tamanho, a menos que um seja um escalar. Um escalar pode ser subtraído de uma matriz de qualquer tamanho.
3	* Multiplicação da matriz. C =A*B é o produto algébrico linear das matrizes A e B. Mais precisamente, 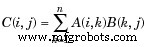Para A e B não escalares, o número de colunas de A deve ser igual ao número de linhas de B. Um escalar pode multiplicar uma matriz de qualquer tamanho.
4	.* Multiplicação de matrizes. A.*B é o produto elemento por elemento dos arrays A e B. A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
5	/ Corte ou divisão à direita da matriz. B/A é aproximadamente o mesmo que B*inv(A). Mais precisamente, B/A =(A'\B')'.
6	./ Divisão direita da matriz. A./B é a matriz com elementos A(i,j)/B(i,j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
7	\ Barra invertida ou divisão à esquerda da matriz. Se A é uma matriz quadrada, A\B é aproximadamente o mesmo que inv(A)*B, exceto que é calculado de uma maneira diferente. Se A é uma matriz n por n e B é um vetor coluna com n componentes, ou uma matriz com várias dessas colunas, então X =A\B é a solução da equação AX =B . Uma mensagem de aviso é exibida se A estiver mal dimensionado ou quase singular.
8	.\ Divisão esquerda da matriz. A.\B é a matriz com elementos B(i,j)/A(i,j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
9	^ Poder da matriz. X^p é X elevado a p, se p é um escalar. Se p é um número inteiro, a potência é calculada pelo quadrado repetido. Se o número inteiro for negativo, X é invertido primeiro. Para outros valores de p, o cálculo envolve autovalores e autovetores, de modo que se [V,D] =eig(X), então X^p =V*D.^p/V.
10	.^ Poder de matriz. A.^B é a matriz com elementos A(i,j) elevado a B(i,j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
11	' Transposição de matriz. A' é a transposição algébrica linear de A. Para matrizes complexas, esta é a transposição conjugada complexa.
12	.' Transposição de matriz. UMA.' é a transposição de matrizes de A. Para matrizes complexas, isso não envolve conjugação.

Operadores Relacionais

Os operadores relacionais também podem funcionar em dados escalares e não escalares. Operadores relacionais para arrays realizam comparações elemento a elemento entre dois arrays e retornam um array lógico do mesmo tamanho, com elementos definidos como lógico 1 (verdadeiro) onde a relação é verdadeira e elementos definidos como lógico 0 (falso) onde é não.

A tabela a seguir mostra os operadores relacionais disponíveis no MATLAB −

Mostrar exemplos

Nº Sr.	Operador e Descrição
1	< Menor que
2	<= Menos que ou igual a
3	> Maior que
4	>= Melhor que ou igual a
5	== Igual a
6	~= Não igual a

Operadores lógicos

O MATLAB oferece dois tipos de operadores lógicos e funções -

• 
  Element-wise – Esses operadores operam em elementos correspondentes de arrays lógicos.
  
• 
  Curto-circuito - Esses operadores operam em expressões escalares e lógicas.
  

Os operadores lógicos elementares operam elemento por elemento em matrizes lógicas. Os símbolos &, | e ~ são os operadores de matriz lógica AND, OR e NOT.

Operadores lógicos de curto-circuito permitem curto-circuito em operações lógicas. Os símbolos &&e || são os operadores lógicos de curto-circuito AND e OR.

Mostrar exemplos

Operações bit a bit

Os operadores bit a bit trabalham em bits e realizam operações bit a bit. As tabelas verdade para &, | e ^ são as seguintes −

p	q	p &q	p | q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Suponha que A =60; e B =13; Agora, em formato binário, eles serão os seguintes -

A =0011 1100

B =0000 1101

-----------------

A&B =0000 1100

A|B =0011 1101

A^B =0011 0001

~A =1100 0011

O MATLAB fornece várias funções para operações bit a bit, como operações 'bit a bit e', 'bit a bit or' e 'bit a bit não', operações de deslocamento, etc.

A tabela a seguir mostra as operações bit a bit comumente usadas -

Mostrar exemplos

Função	Propósito
bitand(a, b)	E bit a bit de inteiros a e b
bitcmp(a)	Complemento bit a bit de a
bitget(a,pos)	Obter bit na posição especificada pos , na matriz de inteiros a
bitor(a, b)	OR bit a bit de inteiros a e b
bitset(a, pos)	Definir bit em local específico pos de um
bitshift(a, k)	Retorna a deslocado para a esquerda por k bits, equivalente a multiplicar por 2 k . Valores negativos de k correspondem a deslocamento de bits para a direita ou divisão por 2 |k| e arredondando para o inteiro mais próximo para infinito negativo. Quaisquer bits de estouro são truncados.
bitxor(a, b)	XOR bit a bit de inteiros a e b
troca de bytes	Trocar a ordem dos bytes

Definir operações

O MATLAB fornece várias funções para operações de conjunto, como união, interseção e teste para associação de conjunto, etc.

A tabela a seguir mostra algumas operações de conjunto comumente usadas -

Mostrar exemplos

Nº Sr.	Função e descrição
1	interseção(A,B) Definir interseção de dois arrays; retorna os valores comuns a A e B. Os valores retornados estão em ordem de classificação.
2	interseção(A,B,'linhas') Trata cada linha de A e cada linha de B como entidades únicas e retorna as linhas comuns a A e B. As linhas da matriz retornada estão em ordem de classificação.
3	émembro(A,B) Retorna um array do mesmo tamanho de A, contendo 1 (verdadeiro) onde os elementos de A são encontrados em B. Em outros lugares, ele retorna 0 (falso).
4	ismember(A,B,'linhas') Trata cada linha de A e cada linha de B como entidades únicas e retorna um vetor contendo 1 (verdadeiro) onde as linhas da matriz A também são linhas de B. Em outros lugares, retorna 0 (falso).
5	sortido(A) Retorna lógico 1 (verdadeiro) se os elementos de A estiverem em ordem de classificação e lógico 0 (falso) caso contrário. A entrada A pode ser um vetor ou uma matriz de cadeias de células N por 1 ou 1 por N. A é considerado classificado se A e a saída de sort(A) são iguais.
6	sorted(A, 'linhas') Retorna lógico 1 (verdadeiro) se as linhas da matriz bidimensional A estiverem em ordem de classificação e lógico 0 (falso) caso contrário. A matriz A é considerada ordenada se A e a saída de sortrows(A) são iguais.
7	setdiff(A,B) Define a diferença de dois arrays; retorna os valores em A que não estão em B. Os valores na matriz retornada estão em ordem de classificação.
8	setdiff(A,B,'linhas') Trata cada linha de A e cada linha de B como entidades únicas e retorna as linhas de A que não estão em B. As linhas da matriz retornada estão em ordem de classificação. A opção 'linhas' não suporta matrizes de células.
9	setxor Define OR exclusivo de dois arrays
10	sindicato Define a união de dois arrays
11	único Valores únicos na matriz