MATLAB - Diferencial
O MATLAB fornece o dif comando para calcular derivadas simbólicas. Em sua forma mais simples, você passa a função que deseja diferenciar para o comando diff como um argumento.
Por exemplo, vamos calcular a derivada da função f(t) =3t 2 + 2t -2
Exemplo
Crie um arquivo de script e digite o seguinte código nele -
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Quando o código acima é compilado e executado, ele produz o seguinte resultado -
ans = 6*t - 4/t^3
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)
Octave executa o código e retorna o seguinte resultado -
ans = -(4.0)*t^(-3.0)+(6.0)*t
Verificação das Regras Elementares de Diferenciação
Vamos enunciar brevemente várias equações ou regras para a diferenciação de funções e verificar essas regras. Para este propósito, escreveremos f'(x) para uma derivada de primeira ordem e f"(x) para uma derivada de segunda ordem.
A seguir estão as regras para diferenciação -
Regra 1
Para quaisquer funções f e g e quaisquer números reais a e b são a derivada da função −
h(x) =af(x) + bg(x) em relação a x é dado por −
h'(x) =af'(x) + bg'(x)
Regra 2
A soma e subtração As regras afirmam que se f e g são duas funções, f' e g' são suas derivadas respectivamente, então,
(f + g)' =f' + g'
(f - g)' =f' - g'
Regra 3
O produto A regra afirma que se f e g são duas funções, f' e g' são suas derivadas respectivamente, então,
(f.g)' =f'.g + g'.f
Regra 4
O quociente A regra afirma que se f e g são duas funções, f' e g' são suas derivadas respectivamente, então,
(f/g)' =(f'.g - g'.f)/g 2
Regra 5
O polinômio ou regra de potência elementar afirma que, se y =f(x) =x n , então f' =n. x (n-1)
Um resultado direto dessa regra é que a derivada de qualquer constante é zero, ou seja, se y =k , qualquer constante, então
f' =0
Regra 6
A cadeia A regra afirma que, derivada da função de uma função h(x) =f(g(x)) em relação a x é,
h'(x)=f'(g(x)).g'(x)
Exemplo
Crie um arquivo de script e digite o seguinte código nele -
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Quando você executa o arquivo, o MATLAB exibe o seguinte resultado -
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3)
der1 = differentiate(f,x)
f = (t^2 + 3)*(t^(1/2) + t^3)
der2 = differentiate(f,t)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = differentiate(f,x)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = differentiate(f,x)
f = (x^2 + 1)^17
der5 = differentiate(f,x)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = differentiate(f,t)
Octave executa o código e retorna o seguinte resultado -
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Derivadas de funções exponenciais, logarítmicas e trigonométricas
A tabela a seguir fornece as derivadas das funções exponenciais, logarítmicas e trigonométricas comumente usadas -
| Função | Derivativo |
|---|---|
| c a.x | c a.x .ln c.a (ln é logaritmo natural) |
| e x | e x |
| ln x | 1/x |
| lnc x | 1/x.ln c |
| x x | x x .(1 + ln x) |
| sin(x) | cos(x) |
| cos(x) | -sin(x) |
| tan(x) | seg 2 (x), ou 1/cos 2 (x), ou 1 + tan 2 (x) |
| berço(x) | -csc 2 (x), ou -1/sin 2 (x), ou -(1 + berço 2 (x)) |
| s(x) | sec(x).tan(x) |
| csc(x) | -csc(x).cot(x) |
Exemplo
Crie um arquivo de script e digite o seguinte código nele -
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Quando você executa o arquivo, o MATLAB exibe o seguinte resultado -
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
y = Exp(x)
differentiate(y,x)
y = x^9
differentiate(y,x)
y = Sin(x)
differentiate(y,x)
y = Tan(x)
differentiate(y,x)
y = Cos(x)
differentiate(y,x)
y = Log(x)
differentiate(y,x)
% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)
y = Sin(x)^2
differentiate(y,x)
y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)
y = Exp(x)/Sin(x)
differentiate(y,x)
Octave executa o código e retorna o seguinte resultado -
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Cálculo de derivativos de ordem superior
Para calcular derivadas mais altas de uma função f, usamos a sintaxe diff(f,n) .
Vamos calcular a segunda derivada da função y =f(x) =x .e -3x
f = x*exp(-3*x); diff(f, 2)
O MATLAB executa o código e retorna o seguinte resultado -
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)
Octave executa o código e retorna o seguinte resultado -
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
Exemplo
Neste exemplo, vamos resolver um problema. Dado que uma função y =f(x) =3 sen(x) + 7 cos(5x) . Teremos que descobrir se a equação f" + f =-5cos(2x) permanece verdadeiro.
Crie um arquivo de script e digite o seguinte código nele -
syms x
y = 3*sin(x)+7*cos(5*x); % defining the function
lhs = diff(y,2)+y; %evaluting the lhs of the equation
rhs = -5*cos(2*x); %rhs of the equation
if(isequal(lhs,rhs))
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Quando você executa o arquivo, ele exibe o seguinte resultado -
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
y = 3*Sin(x)+7*Cos(5*x); % defining the function
lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation
rhs = -5*Cos(2*x); %rhs of the equation
if(lhs == rhs)
disp('Yes, the equation holds true');
else
disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);
Octave executa o código e retorna o seguinte resultado -
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Encontrando os máximos e mínimos de uma curva
Se estamos procurando os máximos e mínimos locais para um gráfico, estamos basicamente procurando os pontos mais altos ou mais baixos no gráfico da função em uma localidade específica, ou por um intervalo específico de valores da variável simbólica.
Para uma função y =f(x) os pontos no gráfico onde o gráfico tem inclinação zero são chamados de pontos estacionários . Em outras palavras, pontos estacionários são onde f'(x) =0.
Para encontrar os pontos estacionários de uma função que derivamos, precisamos igualar a derivada a zero e resolver a equação.
Exemplo
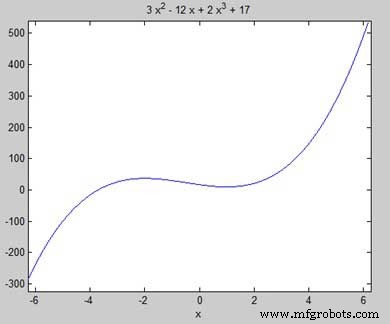
Vamos encontrar os pontos estacionários da função f(x) =2x 3 + 3x 2 − 12x + 17
Siga os seguintes passos -
Primeiro vamos entrar na função e traçar seu gráfico.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
O MATLAB executa o código e retorna o seguinte gráfico -
Aqui está o código equivalente ao Octave para o exemplo acima -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y)
print -deps graph.eps
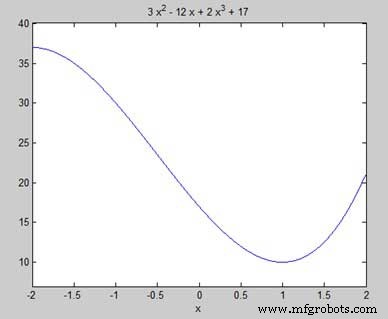
Nosso objetivo é encontrar alguns máximos e mínimos locais no gráfico, então vamos encontrar os máximos e mínimos locais para o intervalo [-2, 2] no gráfico.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
O MATLAB executa o código e retorna o seguinte gráfico -
Aqui está o código equivalente ao Octave para o exemplo acima -
pkg load symbolic
symbols
x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");
ezplot(y, [-2, 2])
print -deps graph.eps
Em seguida, vamos calcular a derivada.
g = diff(y)
O MATLAB executa o código e retorna o seguinte resultado -
g = 6*x^2 + 6*x - 12
Aqui está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
Octave executa o código e retorna o seguinte resultado -
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Vamos resolver a função derivada, g, para obter os valores onde ela se torna zero.
s = solve(g)
O MATLAB executa o código e retorna o seguinte resultado -
s = 1 -2
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
Octave executa o código e retorna o seguinte resultado -
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Isso está de acordo com nosso enredo. Então, vamos avaliar a função f nos pontos críticos x =1, -2. Podemos substituir um valor em uma função simbólica usando as subs comando.
subs(y, 1), subs(y, -2)
O MATLAB executa o código e retorna o seguinte resultado -
ans = 10 ans = 37
A seguir está o equivalente de oitava do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Portanto, os valores mínimo e máximo da função f(x) =2x 3 + 3x 2 − 12x + 17, no intervalo [-2,2] são 10 e 37.
Resolver equações diferenciais
O MATLAB fornece o dsolve comando para resolver equações diferenciais simbolicamente.
A forma mais básica do dsolve comando para encontrar a solução para uma única equação é
dsolve('eqn')
onde eqn é uma string de texto usada para inserir a equação.
Ele retorna uma solução simbólica com um conjunto de constantes arbitrárias que o MATLAB rotula C1, C2 e assim por diante.
Você também pode especificar condições iniciais e de contorno para o problema, como uma lista delimitada por vírgulas seguindo a equação como −
dsolve('eqn','cond1', 'cond2',…)
Para o propósito de usar o comando dsolve, derivados são indicados com um D . Por exemplo, uma equação como f'(t) =-2*f + custo(t) é inserida como −
'Df =-2*f + cos(t)'
Derivadas mais altas são indicadas seguindo D pela ordem da derivada.
Por exemplo, a equação f"(x) + 2f'(x) =5sin3x deve ser inserida como −
'D2y + 2Dy =5*sen(3*x)'
Tomemos um exemplo simples de uma equação diferencial de primeira ordem:y' =5y.
s = dsolve('Dy = 5*y')
O MATLAB executa o código e retorna o seguinte resultado -
s = C2*exp(5*t)
Vamos pegar outro exemplo de uma equação diferencial de segunda ordem como:y" - y =0, y(0) =-1, y'(0) =2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
O MATLAB executa o código e retorna o seguinte resultado -
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB



