MATLAB - Cálculo

MATLAB fornece várias maneiras de resolver problemas de cálculo diferencial e integral, resolver equações diferenciais de qualquer grau e cálculo de limites. O melhor de tudo é que você pode plotar facilmente os gráficos de funções complexas e verificar máximos, mínimos e outros pontos de papelaria em um gráfico, resolvendo a função original, bem como sua derivada.

Este capítulo lidará com problemas de cálculo. Neste capítulo, discutiremos conceitos de pré-cálculo, isto é, calcular limites de funções e verificar as propriedades dos limites.

No próximo capítulo Diferencial , calcularemos a derivada de uma expressão e encontraremos os máximos e mínimos locais em um gráfico. Também discutiremos a resolução de equações diferenciais.

Por fim, na Integração capítulo, discutiremos o cálculo integral.

Cálculo de limites

O MATLAB fornece o limite função para calcular limites. Em sua forma mais básica, o limite A função recebe a expressão como argumento e encontra o limite da expressão à medida que a variável independente vai para zero.

Por exemplo, vamos calcular o limite de uma função f(x) =(x³ + 5)/(x⁴ + 7), pois x tende a zero.

syms x
limit((x^3 + 5)/(x^4 + 7))

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   5/7

A função limite cai no domínio da computação simbólica; você precisa usar o syms para informar ao MATLAB quais variáveis simbólicas você está usando. Você também pode calcular o limite de uma função, pois a variável tende a algum número diferente de zero. Para calcular lim _x->a (f(x)), usamos o comando limit com argumentos. O primeiro é a expressão e o segundo é o número, que x abordagens, aqui está um .

Por exemplo, vamos calcular o limite de uma função f(x) =(x-3)/(x-1), pois x tende a 1.

limit((x - 3)/(x-1),1)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   NaN

Vamos dar outro exemplo,

limit(x^2 + 5, 3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   14

Cálculo de limites usando oitava

A seguir está a versão Octave do exemplo acima usando simbólico pacote, tente executar e comparar o resultado -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

Octave executará a instrução acima e retornará o seguinte resultado -

ans =
   0.7142857142857142857

Verificação das Propriedades Básicas dos Limites

O Teorema Algébrico do Limite fornece algumas propriedades básicas dos limites. Estes são os seguintes -

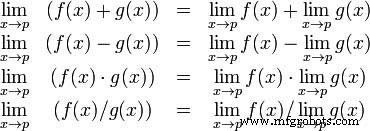
Consideremos duas funções -

f(x) =(3x + 5)/(x - 3)
g(x) =x² + 1.

Vamos calcular os limites das funções como x tende a 5, de ambas as funções e verificar as propriedades básicas dos limites usando essas duas funções e MATLAB.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Quando você executa o arquivo, ele exibe -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Verificação de Propriedades Básicas de Limites usando Oitava

A seguir está a versão Octave do exemplo acima usando simbólico pacote, tente executar e comparar o resultado -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

Octave executará a instrução acima e retornará o seguinte resultado -

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Limites dos lados esquerdo e direito

Quando uma função tem uma descontinuidade para algum valor particular da variável, o limite não existe nesse ponto. Em outras palavras, os limites de uma função f(x) tem descontinuidade em x =a, quando o valor do limite, quando x se aproxima de x pelo lado esquerdo, não é igual ao valor do limite quando x se aproxima do lado direito.

Isso leva ao conceito de limites canhotos e destros. Um limite à esquerda é definido como o limite como x -> a, da esquerda, ou seja, x se aproxima de a, para valores de x a, da direita, ou seja, x se aproxima de a, para valores de x> a. Quando o limite à esquerda e o limite à direita não são iguais, o limite não existe.

Consideremos uma função −

f(x) =(x - 3)/|x - 3|

Mostraremos que lim_x->3 f(x) não existe. O MATLAB nos ajuda a estabelecer esse fato de duas maneiras −

Traçando o gráfico da função e mostrando a descontinuidade.
Calculando os limites e mostrando que ambos são diferentes.

Os limites canhotos e destros são calculados passando as cadeias de caracteres 'esquerda' e 'direita' para o comando limit como o último argumento.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Quando você executa o arquivo, o MATLAB desenha o seguinte gráfico

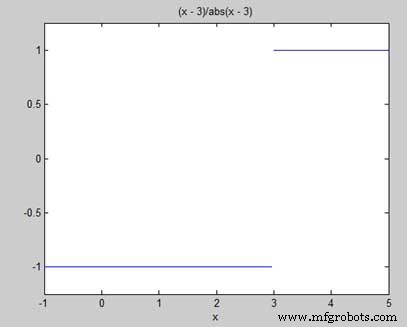
Após a seguinte saída ser exibida -

l =
   -1
  
r =
   1

MATLAB - Álgebra MATLAB - Diferencial

MATLAB