Modelagem de Dinâmica Molecular e Simulação de Corte de Cério com Diamante

Resumo

O acoplamento entre transformações de fase estruturais e deslocamentos induz desafios na compreensão do comportamento de deformação do cério metálico em nanoescala. No presente trabalho, elucidamos o mecanismo subjacente do cério sob o corte de diamante de ultraprecisão por meio de modelagem por dinâmica molecular e simulações. O modelo de dinâmica molecular do corte de diamante de cério é estabelecido atribuindo potenciais empíricos para descrever as interações atômicas e avaliando as propriedades de duas fases cúbicas de cério centradas na face. Simulações de dinâmica molecular subsequentes revelam que o deslizamento de deslocamento domina a deformação plástica do cério durante o processo de corte. Além disso, a análise baseada em funções de distribuição radial atômica demonstra que existem transformações de fase triviais do γ-Ce para o δ-Ce ocorridas tanto na superfície usinada quanto no chip formado. As investigações seguintes sobre a dependência dos parâmetros de usinagem revelam as condições de usinagem ideais para alcançar alta qualidade da superfície usinada de cério.

Histórico

O cério (Ce) com número atômico 58 é um dos metais lantanídeos mais abundantes. O cério tem amplas aplicações por suas intrigantes propriedades mecânicas, físicas e químicas. Sabe-se que a morfologia da superfície usinada de peças metálicas tem forte influência em sua funcionalidade, desempenho e ciclo de vida. Por exemplo, a resistência à corrosão de peças de metal pode ser efetivamente melhorada reduzindo a rugosidade da superfície ou introduzindo tensão residual compressiva na superfície usinada [1,2,3]. Mais recentemente, Yan et al. empregou uma nova técnica de usinagem mecânica baseada em ponta para fabricar microcavidades triangulares periódicas em Cu (111), que é demonstrado ser um substrato de espalhamento Raman com superfície aprimorada [4]. Especificamente para o cério, que é usado para armazenar hidrogênio [5], o acabamento superficial do cério influencia fortemente a reação entre o cério e o hidrogênio à temperatura ambiente. Portanto, atingir alta precisão da morfologia da superfície usinada de cério é crucial para suas aplicações. O corte de diamante de ultraprecisão é uma técnica de fabricação importante para obter um acabamento superficial ultra-liso de alta integridade superficial, ultra-baixa rugosidade superficial, alta planicidade, baixa evolução da estrutura metalográfica e baixo dano subsuperficial [6, 7]. No entanto, trabalhos experimentais ou teóricos sobre o corte de diamante de cério raramente foram relatados. Além disso, como no processo de corte de diamante de ultraprecisão, o raio da aresta da ferramenta é comparável à profundidade de corte, as propriedades do material da peça desempenham um papel importante e dominante no processo de corte. Portanto, o entendimento dos mecanismos de usinagem do cério é desafiador por seu complexo comportamento de deformação.

Em primeiro lugar, o cério é conhecido por seu diagrama de fases de pressão-temperatura extraordinariamente rico, conduzido pela deslocalização de elétrons 4f. Na pressão atmosférica e em baixas temperaturas abaixo de 110 K, o α-Ce (cúbico centrado na face (fcc)) é estável. Em temperaturas aumentadas variando de 45 a 275 K, o α-Ce se transforma em β-Ce (duplo hexagonal fechado (dhcp)). O γ-Ce (fcc) é estável em temperaturas moderadas entre 270 e 999 K. Em altas temperaturas entre 999 K e a temperatura de fusão de 1071 K, o δ-Ce (cúbico centrado no corpo (bcc)) é estável [8,9 , 10,11]. Em particular, a transformação de fase isoestrutural mais fascinante do γ-Ce trivalente de baixa densidade para o α-Ce muito mais denso em 295 K e abaixo de 8 kbar é acompanhada por um colapso de grande volume de 20% [8, 12,13,14 ] A modificação induzida por transformação de fase da estrutura eletrônica e configuração de ligação no cério inevitavelmente tem um forte impacto em seu comportamento de deformação. Especificamente, a alta temperatura e a alta pressão formadas na região de contato entre a ferramenta de corte e a peça de trabalho podem resultar na transformação de fase do cério no processo de corte de diamante. Em segundo lugar, o cério metálico tem considerável ductilidade governada por luxações [15]. Sabe-se que a nucleação por deslocamento e o deslizamento desempenham papéis importantes na deformação plástica de metais FCC sob usinagem mecânica. No entanto, ainda é amplamente desconhecido sobre a interação entre transformações de fase e deslocamentos no corte de diamante de cério.

Os constituintes dos mecanismos de usinagem consistem no comportamento de deformação microscópica do material da peça e sua correlação com os resultados da usinagem macroscópica em termos de força de corte, perfil do cavaco e morfologia da superfície usinada. Como um importante complemento aos experimentos de usinagem, a simulação de dinâmica molecular (MD) demonstrou ser uma ferramenta poderosa para elucidar os mecanismos fundamentais de usinagem mecânica de diferentes tipos de materiais. Li et al. relataram que a profundidade mínima de desgaste de Cu (111) cristalino único sob nanoscratching que é equivalente à profundidade de penetração crítica na qual a plasticidade inicia aumenta com o raio da sonda [16]. Mais recentemente, eles investigaram os comportamentos mecânicos e os mecanismos de deformação das ligas de alta entropia AlCrCuFe sob nanoscratching e relataram um volume de acúmulo de superfície maior do que os metais puros devido à sua boa estabilidade em alta temperatura do material da liga [17]. Gao et al. investigou a geração e evolução da plasticidade e defeitos no corte ortogonal de um bcc Fe [18]. Zhu et al. relataram um efeito de tamanho na dependência do formato da sonda do nanoscratching [19]. Hosseini et al. investigou os efeitos do raio da aresta da ferramenta na nanomáquina de cobre monocristalino [20]. Liu et al. descobriram que a diferença entre os coeficientes de atrito estático e dinâmico desaparecem no atrito de aspereza única de Cu (111) devido à interferência entre as asperezas [21]. Romero et al. descobriram que a adesão durante o corte ortogonal de um substrato de cobre pode ser reforçada variando o ângulo de inclinação da ferramenta e escolhendo orientações de rede específicas [22]. Yang et al. indicaram que a velocidade e direção de autorrotação do abrasivo têm influência significativa na morfologia e na qualidade da superfície usinada de cobre monocristalino sob polimento [23]. Vargonen et al. relataram que a perda de altura da ponta por distância de raspagem durante a raspagem é uma função da tensão normal e do ângulo de afilamento da ponta [24]. Sun et al. impacto comprovado do GB no arranhão do cobre bicristal [25]. Chen et al. descobriram que as moléculas de água reduzem efetivamente o atrito entre a ferramenta e a peça no corte nanométrico de cobre [26]. Wu et al. relataram que a energia de ligação tem influência significativa no atrito [27]. Além disso, em comparação com as investigações experimentais, as propriedades mecânicas de cada fase do cério podem ser convenientemente estudadas por meio de simulações MD, o que é crucial para o entendimento da interação entre as transformações de fase e os deslocamentos no cério. Mais recentemente, Zhang et al. investigaram as interações entre transformação de fase e deslocamento na transição elástico-plástica em nanoindentação de silício por simulações de MD [28]. No entanto, até onde sabemos, não há nenhum trabalho relatado na investigação MD de usinagem mecânica de cério.

Portanto, no presente trabalho, primeiro estabelecemos o modelo MD de corte de diamante de cério construindo configurações atômicas de peça e ferramenta, atribuindo potenciais empíricos para as interações atômicas Ce-Ce e Ce-C, e caracterizando duas fases fcc do cério. Com o modelo MD estabelecido, realizamos simulações MD de corte de cério com diamante para elucidar os mecanismos fundamentais de usinagem de cério e investigar as influências do ângulo de saída da ferramenta de corte e orientação cristalográfica da peça no processo de corte.

Métodos

Modelo MD de corte com diamante

A Figura 1 mostra o modelo MD de corte de diamante, que consiste em uma única peça de cristal de cério e uma ferramenta de corte de diamante. A peça de cério tem uma dimensão de 41, 25 e 31 nm nas direções horizontal, vertical e longitudinal, respectivamente, e consiste em um milhão de átomos γ-Ce na estrutura fcc. A condição de contorno periódica só é aplicada na direção longitudinal. A peça consiste em dois tipos de átomos, como átomos inferiores e átomos móveis, respectivamente. A camada de átomos inferiores com espessura de 2 nm é fixada no espaço para evitar qualquer movimento rígido da peça de trabalho. O movimento dos átomos móveis segue a equação de movimento de Newton com o algoritmo de integração velocidade-verlet. A temperatura de cada átomo na peça é monitorada no processo de corte para representar a dissipação de calor gerada. Para abordar a influência da orientação cristalográfica, três peças de cério com (010), (110) e (111) superfície livre na direção vertical são consideradas. A ferramenta de corte de diamante com aresta viva possui um ângulo de relevo de 9 ° e é composta por 0,1 milhão de átomos de C na estrutura do diamante. Sete ângulos de inclinação, como −30 °, −20 °, −10 °, 0 °, 10 °, 20 ° e 30 °, são utilizados para avaliar a influência do ângulo de inclinação. Dada a dureza ultra-alta do diamante em comparação com o cério e a distância de corte ultra-curta, o desgaste da ferramenta de diamante durante o processo de corte não é considerado. Portanto, a ferramenta de corte de diamante é definida como um corpo rígido, ou seja, as coordenadas e velocidades de todos os átomos na ferramenta de corte são atualizadas a cada passo de tempo, de modo que a ferramenta de corte se mova como uma entidade única, sem qualquer deformação.

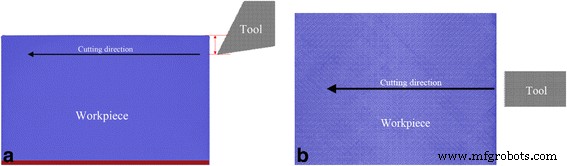
Modelo MD de corte de cério com diamante; (cor online) Modelo MD de lapidação de cério com diamante. a Vista frontal e b vista superior . Vermelho e cores azuis representam átomos de Ce inferior e móvel, e cor cinza indica átomos C

Existem três tipos de interações atômicas no sistema simulado, como Ce-Ce na peça de cério, Ce-C entre a peça de cério e a ferramenta de corte de diamante e C-C na ferramenta de corte de diamante, respectivamente. As interações C-C são omitidas, pois a ferramenta de corte de diamante é tratada como um corpo rígido sem nenhuma deformação no processo de corte. O método do átomo incorporado (EAM) composto de potencial de par interagente e energia de incorporação de elétrons tem sido amplamente utilizado para descrever sistemas metálicos, que podem ser expressos como
$$ {E} _ {\ mathrm {tot}} =\ frac {1} {2} {\ sum} _ {i, j} {\ phi} _ {ij} \ left ({r} _ {ij} \ right) + {\ sum} _i {F} _i \ left ({\ rho} _i \ right) $$ (1) $$ {\ rho} _i ={\ sum} _ {j \ ne i} {\ rho} _i \ left ({r} _ {ij} \ right) $$ (2)
onde r _ij é a distância entre os átomos i e j , ϕ _ij é o potencial do par entre átomos i e j , F _i representa a energia de incorporação que é gerada quando um átomo i está incorporado, ρ _i é a densidade do elétron em i átomo gerado por todos os átomos, exceto átomo i e ρ _j é uma função da densidade do elétron do átomo j no átomo i . Os parâmetros EAM para cério por Sheng et al. são utilizados para descrever as interações Ce-Ce, que são capazes de descrever com precisão as propriedades elásticas em massa das fases de cério fcc [29]. O potencial de Morse é utilizado para descrever a interação Ce-C, que pode ser expressa como
$$ {E} _ {\ mathrm {tot}} ={\ sum} _ {ij} {D} _0 \ left [{e} ^ {- 2 \ alpha \ left (r-r0 \ right)} - 2 {e} ^ {- \ alpha \ left (r-r0 \ right)} \ right] $$ (3)
onde D ₀ (0,087 eV) é a energia coesiva, α (5,14) é o módulo de elasticidade, e r ₀ (2,93 Å) representa a distância de equilíbrio entre os átomos i e j , respectivamente. O raio de corte do potencial de Morse é escolhido como 1,0 nm [30].

O sistema de simulação criado é primeiro equilibrado com sua configuração de equilíbrio a 30 K e abaixo de 0 bar no conjunto NPT (número constante de átomos N , pressão constante P , e temperatura constante T ) Em seguida, a peça equilibrada é submetida ao corte de diamante com velocidade constante de 100 m / se profundidade de corte de 4 nm no conjunto canônico (número constante de átomos N , volume constante V , e temperatura constante T ) A direção de corte é indicada por setas coloridas em vermelho em diferentes pontos de vista do modelo de corte. E a força de corte é definida como o componente da força ao longo da direção de corte. A profundidade de corte utilizada no experimento de usinagem de ultraprecisão é de alguns micrômetros. Notamos que a dimensão simulada da peça e a profundidade de corte são várias ordens de magnitude menores do que as utilizadas em experimentos de corte de diamante de ultraprecisão, devido à limitação da escala de comprimento em simulações atomísticas. Observamos também que a velocidade de corte empregada de 100 m / s nas simulações atuais de MD de corte nanométrico é várias ordens de magnitude maior do que as velocidades típicas de dezenas de micrômetros por segundo utilizadas em experimentos de corte de diamante de ultraprecisão, dando o requisito intrínseco do intervalo de tempo de integração para ser da ordem do femtossegundo (fs). A análise de vizinho comum (CNA) é utilizada para identificar os tipos de defeitos de rede [31], e o esquema de coloração é o seguinte:verde significa átomos fcc, vermelho significa átomos hexagonais compactados (hcp), azul significa cúbico centrado no corpo átomos (bcc) e cinza para outros átomos, incluindo átomos de superfície e núcleos de deslocamento. Todas as simulações de MD são realizadas usando o código LAMMPS com um intervalo de tempo de integração de 1 fs [32]. E o OVITO é utilizado para visualizar dados de MD e gerar instantâneos de MD [33].

Caracterização das fases de cério

No presente trabalho, cinco fases de cério são consideradas, como γ, α, β, ε e δ, respectivamente. A Tabela 1 lista os parâmetros estruturais e as condições de temperatura-pressão relacionadas para cada fase que são coletadas de literaturas [8,9,10,11]. A configuração atômica em massa de cada fase é então construída de acordo com a Tabela 1. E então, simulações computacionais de tensão uniaxial, cisalhamento e compressão uniforme de configurações em massa conforme construída são conduzidas para derivar propriedades mecânicas de diferentes fases Ce. Devido à alta temperatura estável próxima ao ponto de fusão do cério, as propriedades mecânicas do δ-Ce não são calculadas, pois é difícil realizar testes mecânicos na fase líquida. A Tabela 2 lista as constantes elásticas derivadas e propriedades mecânicas de cada fase de cério. O módulo de Young calculado da fase γ-Ce cristalina única é 24,17 GPa, que é comparável com o valor experimental de 36,7 GPa relatado na nanoindentação de sua contraparte policristalina [10]. Além disso, os valores calculados de C44 e 1/2 (c11-c12) diferem por um fator de 3, o que concorda bem com o valor experimental usando técnicas de espalhamento inelástico de nêutrons [34]. A Tabela 2 demonstra que o α-Ce mais denso tem propriedades mecânicas significativamente aprimoradas em comparação com sua fase γ-Ce de baixa densidade isoestrutural.

A função de distribuição radial (RDF), definida como as variações de densidade em um sistema de partículas com a distância de uma partícula de referência na forma de picos agudos. O RDF pode ser deduzido de espectros de raios-X e dados de difração de nêutrons [35, 36]. Portanto, é uma das ferramentas mais importantes para a caracterização estrutural de líquidos e sólidos e atua como um elo importante entre arranjos atômicos microscópicos e propriedades macroscópicas. No estudo atual, o RDF é utilizado para caracterizar diferenças estruturais entre diferentes fases de cério. A Figura 2a representa os histogramas RDF para as cinco fases de cério, em que os picos representam as características da estrutura de rede correspondente:a primeira, a segunda e a terceira distância do vizinho mais próximo do γ-Ce é 3,64, 5,13 e 6,3 Å, respectivamente; a primeira, a segunda e a terceira distâncias vizinhas mais próximas do α-Ce são 3,41, 4,85 e 5,92 Å, respectivamente; a primeira e a segunda distância do vizinho mais próximo do δ-Ce é 3,53 e 6,75 Å, respectivamente; a primeira, segunda, terceira e quarta distâncias vizinhas mais próximas do ε-Ce são 2,96, 3,33, 4,91 e 5,69 Å, respectivamente; a primeira, segunda, terceira e quarta distâncias vizinhas mais próximas do β-Ce são 3,71, 3,97, 5,27 e 5,92 Å, respectivamente. Para demonstrar a viabilidade de prever transformações de fase entre duas fases fcc cério pelos parâmetros de potencial EAM empregados, a compressão uniforme do γ-Ce bruto até atingir um colapso de volume de 20% é realizada. A Figura 2b apresenta o RDF antes e depois da compressão, que respectivamente coincide bem com o RDF do γ-Ce e do α-Ce, indicando a ocorrência da mais conhecida transformação de fase γ ➔ α [12,13,14] .

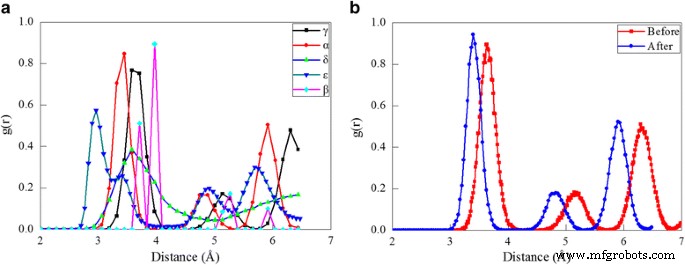
Análise RDF de fases de cério; (cor online) a RDF de fases de cério. b RDF antes e depois da compressão do γ-Ce

Resultados e discussão

Mecanismos de usinagem de cério

A simulação MD de corte de diamante de Ce (010) é realizada pela primeira vez para elucidar os mecanismos fundamentais de usinagem de cério. A ferramenta de corte de diamante utilizada tem um ângulo de ataque de 0 °. Existem três componentes da força de usinagem, como força de corte ao longo da direção horizontal, força normal perpendicular à superfície usinada e força lateral ao longo da direção longitudinal, respectivamente. A Figura 3 mostra as variações da força de corte e força normal com o comprimento de corte durante o processo de corte, que são categorizadas em três zonas de acordo com o comprimento de corte. Consequentemente, a subfigura em cada zona mostra a configuração de corte representativa, na qual os átomos são coloridos de acordo com seus valores CNA, e os átomos fcc não são mostrados para uma visualização clara dos defeitos.

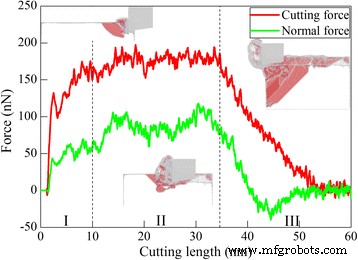
Variação da força de usinagem; (cor online) variação da força de corte e força normal com o comprimento de corte durante o corte do diamante de Ce (010) sob um ângulo de ataque de 0 °. As subfiguras apresentam configurações de defeitos representativas em diferentes zonas, nas quais os átomos são coloridos de acordo com seus valores de CNA.

É visto na Fig. 3 que tanto a força de corte quanto a força normal têm valores negativos quando a ferramenta de corte está bem próxima à peça, devido à aderência entre a ferramenta de corte e a peça de trabalho. Quando a ferramenta de corte começa a entrar em contato com a peça de trabalho, o material primeiro sofre deformação elástica, acompanhada de aumentos rápidos da força de corte e da força normal. A Figura 3 mostra que tanto a força de corte quanto a força normal caem rapidamente em um comprimento de corte de 2,3 nm, indicando o início da deformação plástica. Após o corte adicional, tanto a força de corte quanto a força normal aumentam com fortes flutuações causadas por eventos de nucleação sucessivos. É visto na subfigura na zona II que existem consideráveis deslocamentos parciais 1/6 <112> Shockley gerados nas proximidades da zona de corte. Tanto a força de corte quanto a força normal oscilam principalmente em torno de valores constantes no comprimento de corte que variam de 10 a 35 nm, indicando que o processo de corte é estável. E os deslocamentos na zona II residem principalmente na frente e abaixo da ferramenta de corte de diamante. Quando o comprimento de corte atinge 35 nm, a ferramenta de corte começa a se separar da peça de trabalho, acompanhada por diminuições significativas da força de corte e da força normal. A subfigura na zona III mostra que há deslocamentos consideráveis bloqueados pelo lado esquerdo da peça de trabalho. Tanto a força de corte quanto a força normal se tornam estáveis até que o cavaco formado seja completamente separado da peça de trabalho. A Figura 3 mostra que durante o processo de corte, a força normal é menor do que a força de corte.

A Figura 4a-d apresenta estruturas de defeitos instantâneos dentro da peça em diferentes comprimentos de corte. Os átomos são coloridos de acordo com seus valores CNA, e os átomos fcc não são mostrados. Consequentemente, a Fig. 4e-h apresenta morfologias de superfícies usinadas coloridas por suas alturas atômicas. A inspeção dinâmica da evolução do defeito mostra que o escoamento da peça de trabalho é acompanhado pela nucleação de deslocamentos parciais 1/6 <112> Shockley da superfície livre do lado direito e seu deslizamento subsequente em planos deslizantes {111} adjacentes e ao longo das direções de deslizamento <110>. O movimento dos deslocamentos parciais de Shockley é acompanhado pela expansão das falhas de empilhamento que são delimitadas por núcleos de deslocamento. Com o progresso do processo de corte, uma grande quantidade de deslocamentos parciais é emitida da superfície livre superior na frente da ferramenta de corte, o que leva a cavacos consideráveis formados ao longo da face de inclinação da ferramenta de corte, como mostrado na Fig. 4f. Simultaneamente, os deslocamentos atrás da ferramenta de corte movem-se para cima para aniquilar na superfície livre superior, levando a uma recuperação significativa da superfície usinada. A Figura 4c mostra que quando a ferramenta de corte se aproxima do limite esquerdo da peça de trabalho, a propagação dos deslocamentos é fortemente bloqueada pela superfície livre do lado esquerdo, acompanhada por um volume de cavacos significativamente aumentado, conforme mostrado na Fig. 4g. A Figura 4d mostra que após a separação completa entre o cavaco e a peça de trabalho, a densidade de deslocamento dentro da peça diminui significativamente devido à aniquilação de deslocamento na superfície livre superior.

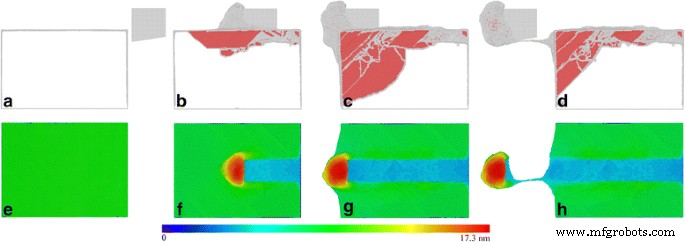
Estruturas de defeitos e morfologias de superfícies usinadas; (cor online) Instantâneos de MD de estruturas de defeitos instantâneos ( linha superior ) e morfologia da superfície usinada ( linha inferior ) no corte de diamante de Ce (010) sob um ângulo de ataque de 0 °. Comprimentos de corte: a , e 0,0 nm, b , f 18,8 nm, c , g 44,8 nm e d , h 59,6 nm. Átomos na linha superior e linha inferior são coloridos de acordo com seus valores de CNA e alturas atômicas, respectivamente

Além da plasticidade dominada por deslizamento de deslocamento, a probabilidade de transformação de fase no processo de corte de diamante também é avaliada pela realização de análise RDF na zona de defeito dentro da peça de trabalho e cavacos formados. O γ-Ce na estrutura fcc é primeiro excluído no OVITO usando o algoritmo CNA, e os átomos restantes são compostos de zonas de defeito incluindo bcc, hcp e outros átomos. Em seguida, a análise RDF é realizada na zona de defeito. E a quantidade de diferentes fases Ce pode ser deduzida pelo número de diferentes tipos de átomos defeituosos. A Figura 5a mostra que os três picos do RDF da zona de defeito abaixo da superfície usinada coincidem bem com os três picos exatos do RDF do δ-Ce, sugerindo a ocorrência de transformação de fase do γ-Ce para o δ-Ce. Enquanto o δ-Ce é estável em alta temperatura e baixa pressão, a transformação de fase γ ➔ δ ocorrida indica a alta dissipação de calor gerada no processo de corte. Além disso, como o δ-Ce possui propriedades mecânicas diferentes da fase γ-Ce, o δ-Ce gerado leva à usinagem heterogênea no processo de corte subsequente. A Figura 5b indica que também existem átomos δ-Ce detectados nos cavacos formados, principalmente devido à transformação de fase γ ➔ δ disparada por alta temperatura na região de contato entre o cavaco formado e a superfície de inclinação da ferramenta de corte. No entanto, a quantidade de δ-Ce formado tanto na zona de defeito quanto no chip é muito trivial, indicando que a transformação de fase não é proeminente no corte de diamante de cério.

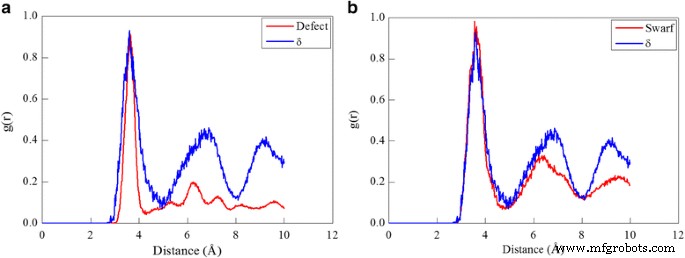
Análise da transformação de fase no processo de corte; (cor online) análise da transformação de fase no corte de diamante de Ce (010) sob um ângulo de ataque de 0 °. RDF de a peça de trabalho e b lasca após o corte

Influência do ângulo de rake

Com o conhecimento fundamental dos mecanismos de usinagem do cério, estuda-se a influência do ângulo de saída da ferramenta de corte no corte do diamante. A Figura 6 representa os valores médios da força de corte e da força normal para os sete ângulos de ataque. O valor médio de cada componente de força é calculado pela média dos valores de força instantânea no comprimento de corte variando de 10 a 35 nm. A Figura 6 mostra que a força de corte é maior do que a força normal para cada ângulo de ataque. No entanto, o valor diferencial dos dois componentes da força é mais pronunciado para um ângulo de ataque maior. Além disso, tanto a força de corte quanto a força normal diminuem com o aumento do ângulo de saída. De acordo com a teoria do Merchant, com o aumento do ângulo de ataque, o ângulo do plano de cisalhamento correspondente à energia mínima também aumenta, o que, consequentemente, diminui a força de corte [37]. A variação da força de usinagem dependente do ângulo de ataque revelada pelas atuais simulações de MD concorda bem com a teoria do comerciante.

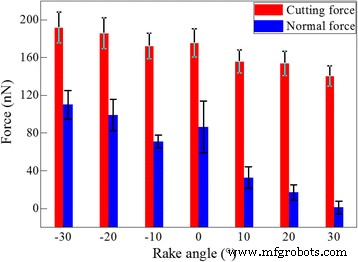
Dependência do ângulo de ancinho da força de usinagem; (cor online) influência do ângulo de ataque na força de usinagem

A Figura 7a, b apresenta uma vista inferior da estrutura com defeito abaixo da superfície usinada após a conclusão do processo de corte de diamante com um ângulo de ataque de −30 ° e 30 °, respectivamente. Para cada ângulo de ataque, os tipos de deslocamento e a geometria do deslocamento em relação à superfície livre são iguais. No entanto, a densidade de deslocamento é significativamente maior para o ângulo de ataque de −30 ° do que para o ângulo de ataque de 30 °, indicando que ocorreu uma deformação plástica mais complexa. A Figura 7c apresenta o número de segmentos de deslocamento que permaneceram dentro da peça após o corte de diamante com diferentes ângulos de ataque, indicando que a densidade de deslocamento diminui com o aumento do ângulo de ataque. Deve-se notar que diferentes tipos de luxações categorizadas pelos vetores Burgers, incluindo 1/2 <110> luxação perfeita, 1/6 <112> luxação parcial de Shockley, 1/6 <110> luxação da haste da escada e 1/3 <111> Deslocamentos parciais francos são levados em consideração na Fig. 7c. No processo de corte nanométrico, a deformação microscópica mediada por deslocamento do material da peça tem uma forte correlação com os resultados da usinagem macroscópica em termos de força de usinagem e morfologia da superfície usinada. Por exemplo, a interação e a reação dos deslocamentos levam à formação de estruturas de deslocamento sésseis que bloqueiam o movimento de deslocamento subsequente; conseqüentemente, o endurecimento por trabalho resultante leva ao aumento da força de usinagem. A aniquilação dos deslocamentos na superfície livre leva à recuperação da superfície usinada, acompanhada com a formação de empilhamento superficial [38].

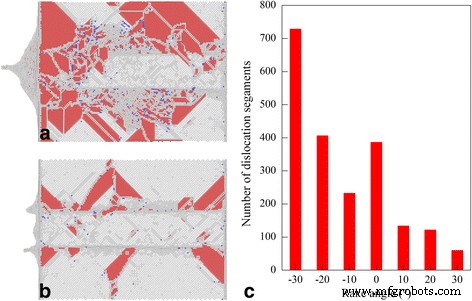
Estruturas de defeitos geradas com diferentes ângulos de ataque; (cor online) Instantâneos MD de estruturas defeituosas após o corte de Cério com ângulo de ataque de a −30 ° e b 30 °. Os átomos são coloridos de acordo com seus valores CNA. c Número de deslocamento dependente do ângulo de ancinho

A Figura 8 apresenta as morfologias da superfície usinada após a conclusão dos processos de corte para diferentes ângulos de ataque. O volume da pilha de superfície em ambos os lados da ranhura formada é mais pronunciado para o ângulo de ataque com valores negativos do que para positivos. Além disso, a distribuição da pilha de superfície é menos uniforme para o ângulo de saída negativo do que para o ângulo de saída positivo. A Figura 8c mostra claramente a distribuição de assimetria da pilha superficial ao longo da ranhura formada para o ângulo de ataque de −30 °. É visto na Fig. 8 que o volume da pilha de superfície diminui com o aumento do ângulo de ataque. Portanto, é indicado que o ângulo de saída de 30 ° é ideal para o corte de diamante de cério para a menor força de usinagem, a menor densidade de deslocamento e a menor empilhamento superficial do que os outros ângulos de saída.

Dependência do ângulo de ancinho das morfologias da superfície usinada; (cor online) morfologia da superfície usinada com diferentes ângulos de ataque: a −10 °, b −20 °, c −30 °, d 10 °, e 20 ° e f 30 °. Os átomos são coloridos de acordo com suas alturas atômicas

Influência da orientação do cristal da peça de trabalho de cério

A influência da orientação do cristal no corte de diamante de cério sob o ângulo de ataque ideal de 30 ° também é investigada. Todos os parâmetros de usinagem são iguais para Ce (010), Ce (110) e Ce (111). A Figura 9 mostra variações de força de corte e número de deslocamento com diferentes orientações de cristal. A força de corte de Ce (010) é significativamente menor do que a de Ce (110) e Ce (111). Embora o número de deslocamento seja o mais baixo em Ce (111), a densidade de deslocamento em Ce (010) é significativamente menor do que em Ce (110). É conhecido que a geometria entre o plano de deslizamento e a superfície livre varia com a orientação do cristal. Para Ce (010) e Ce (110), os quatro planos deslizantes {111} são inclinados para a superfície usinada. No entanto, há um {111} plano de deslizamento paralelo à superfície usinada de Ce (111), além de três {111} planos de deslizamento inclinados. Enquanto a deformação microscópica do material da peça é dominada por deslizamentos de deslocamento, os resultados de usinagem macroscópicos observados em termos de superfície usinada e força de usinagem também podem ser influenciados pela morfologia da superfície usinada. Although the easy glide of dislocations on the {111} slip plane parallel to free surface is energetically favorable for the accommodation of plastic strain caused by cutting tool action, the resulting considerable surface pile up increases the machining resistance, which leads to a high cutting force.

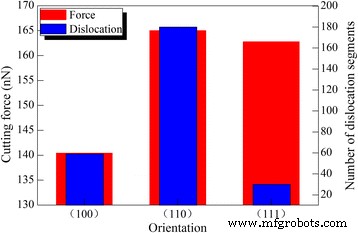
Crystal orientation dependence of cutting force and dislocation number; (color online) crystal orientation dependence of cutting force and dislocation number

Figure 10a–c presents machined surface morphology of Ce(010), Ce(110), and Ce(111), respectively, indicating that the crystal orientation has a strong influence on machined surface quality. The volume of surface pile up is the smallest for Ce(010), followed by Ce(111), and the largest for Ce(110). Correspondingly, the material removal in the form of chip is the most pronounced for Ce(010). Furthermore, it is seen that the surface pile up of Ce(111) on both side of formed groove presents the highest symmetry, while that of Ce(110) is the worst. Therefore, it is indicated that the crystal orientation of (010) is optimal for the diamond cutting of cerium due to its low machining force, low dislocation density, and low surface pile up.

Crystal orientation dependence of machined surface morphology; (color online) crystal orientation dependence of machined surface morphology. Atoms are colored according to atomic heights. Crystal orientation. a (010). b (110). c (111)

Conclusions

In summary, we perform MD modeling and simulation to elucidate the underlying mechanisms of cerium under the ultra-precision diamond cutting. The EAM and Morse potentials are respectively employed to describe atomic interactions within cerium workpiece and the interactions between cerium workpiece and diamond cutting tool. The elastic constants, mechanical properties, and propensity of phase transformation of cerium phases are evaluated, which demonstrates the feasibility of predicting phase transformation of cerium by the current established MD model. Subsequent MD simulations of diamond cutting reveal that the plastic deformation of cerium is governed by dislocation nucleation and subsequent glide, which is similar with other fcc metals. In addition, there is γ ➔ δ phase transformation occurred within both machined surface and formed chip. It is found that high quality of machined surface and low machining force can be achieved in the diamond cutting of cerium with the optimal machining conditions, i.e., a rake angle of 30° for a crystal orientation of (010).

Absorvedor perfeito de banda larga com monocamada MoS2 e matriz hexagonal de nitreto de titânio nanodisco Estratégia de sinterização hidrotérmica para material de ânodo LiNb3O8 estruturado poroso e oco

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias