Efeito de superfície no transporte de petróleo em nanocanais:um estudo de dinâmica molecular

Resumo

Neste trabalho, investigamos o mecanismo de dinâmica do transporte de óleo em nanocanais usando simulações de dinâmica molecular. É demonstrado que a interação entre moléculas de óleo e nanocanal tem um grande efeito nas propriedades de transporte do óleo em nanocanal. Por causa das diferentes interações entre as moléculas de óleo e o canal, o deslocamento do centro de massa (COM) do óleo em um canal de 6 nm é 30 vezes maior do que em um canal de 2 nm, e o coeficiente de difusão das moléculas de óleo no centro de um canal de 6 nm é quase duas vezes mais do que perto da superfície do canal. Além disso, descobriu-se que a polaridade das moléculas de óleo tem o efeito de impedir o transporte de óleo, porque a interação eletrostática entre as moléculas de óleo polares e o canal é muito maior do que entre as moléculas de óleo não polar e o canal. Além disso, o componente do canal desempenha um papel importante no transporte de óleo em nanocanais, por exemplo, o deslocamento COM do óleo no canal de ouro é muito pequeno devido à grande interação entre o óleo e o substrato de ouro. Também foi descoberto que a rugosidade nanométrica da superfície do canal influencia muito a velocidade e o padrão de fluxo do óleo. Nossos resultados contribuiriam para revelar o mecanismo de transporte de óleo em nanocanais e, portanto, são muito importantes para o projeto de extração de óleo em nanocanais.

Histórico

Inspirado na crescente demanda mundial por energia e no consumo excessivo de energia convencional, o desenvolvimento do óleo de xisto não convencional tem ganhado grande atenção, devido às suas grandes reservas e potencial de produção [1]. O óleo de xisto é abreviação de óleo de xisto orgânico maduro e a energia mais representativa listada nas rubricas de energia não convencional. Embora o total de recursos mundiais conhecidos de óleo de xisto seja mais de três vezes maior do que o do petróleo bruto convencional restante [2], as reservas exploráveis ​​totais de óleo de xisto foram estimadas em muito menos do que as reservas. Além disso, o xisto betuminoso tem sido explorado há cerca de 200 anos, mas o desenvolvimento e a utilização do óleo de xisto são muito restritos até agora. Tudo isso sugere que o óleo de xisto, confinado em nanocanal, é difícil de ser extraído [3]. O tamanho do canal do xisto betuminoso varia de 2 a 100 nm de largura [4, 5], o que gera uma grande área de superfície específica e muitos tipos de efeito de superfície. Sob a influência da interação superficial entre fluido e substrato, muitos novos fenômenos físicos podem ser desencadeados, por exemplo, a água flui muito mais rápido dentro dos nanotubos do que em um tubo clássico em macroescala [6, 7], aumento anômalo é encontrado na capacitância de carbono no poro tamanhos menores que 1 nm [8], a afinidade da água no nanotubo de carbono muda de hidrofóbico para hidrofílico conforme a largura diminui [9]. Por estar localizado no xisto betuminoso, com forte interação superficial entre os fluidos e o substrato do xisto, o fluido exibe muitos caracteres diferentes daquele do canal macroscópico, como distribuição de densidade, molhabilidade e coeficiente de difusão [10,11,12], resultando em diferentes propriedades de transporte de fluidos através de tal nanocanal daqueles no canal de macroescala. Usando simulações de dinâmica molecular (MD), Chen et al. investigaram o comportamento de transporte da água dentro de um modelo de nanotubo de carbono e descobriram que a tensão de cisalhamento entre o fluido e o canal era sensível ao tamanho, e também verificaram as conclusões simuladas por experimento em um carbono nanoporoso em glicerina [13]. Xue et al. consideraram o fluxo de decano em nanocanais de sílica sob a força motriz da inundação de gás e descobriram que a pressão inicial e a energia de interação entre o óleo e o substrato desempenharam um papel importante no deslocamento das gotas de óleo [14]. Wang et al. simularam o fluxo de octano em fendas de quartzo por simulações de MD, e descobriram que a velocidade aumentou com o aumento da força externa, largura do canal e temperatura, e também descobriram que o efeito de superfície pode dominar o transporte de óleo no nanocanal com diminuindo a largura do canal [15]. Como mencionado acima, a forte interação de superfície entre os fluidos e o nanocanal tem um efeito crucial no fluxo do fluido no nanocanal. No entanto, há poucos estudos sistemáticos sobre o efeito das propriedades da superfície no mecanismo dinâmico de transporte de óleo em nanocanais. Compreender a influência do efeito de superfície no transporte do óleo de xisto em nanocanais é de grande importância para promover o desenvolvimento e a utilização do óleo de xisto.

Neste trabalho, investigamos o mecanismo de dinâmica do transporte de óleo em nanocanais usando simulações MD e demonstramos que a interação da superfície entre as moléculas de óleo e a superfície do canal, a rugosidade da superfície do canal e a interação entre as moléculas de óleo têm grandes efeitos no centro de massa. (COM) deslocamento de óleo em nanocanal. A conclusão não só fornecerá um futuro brilhante para o campo de energia, mas também lançará luz sobre uma ampla gama de ciências naturais, como meio ambiente, biomedicina, química, energia e aplicações industriais, incluindo translocação de proteínas, separação por membrana de misturas e bateria de canais [16,17,18,19,20].

Métodos

Todas as simulações de MD são realizadas pelo código Discover no software Material Studio (Accelrys Inc.). Um potencial molecular otimizado de fase condensada para estudos de simulação atomística (COMPASS) é usado para descrever as interações interatômicas. O campo de força COMPASS é um campo de força geral de todos os átomos baseado em ab initio e parametrizado usando dados extensos para moléculas na fase condensada. O potencial do campo de força pode ser expresso da seguinte forma:
$$ {E} _ {\ mathrm {total}} ={E} _ {\ mathrm {valência}} + {E} _ {\ mathrm {cross} - \ mathrm {termo}} + {E} _ {\ mathrm {nonbond}} $$ (1)
Na equação acima, E _valência refere-se à energia de valência (ou ligação), que geralmente é explicada por termos diagonais, como alongamento da ligação, curvatura do ângulo de valência, torção do ângulo diédrico e inversão. E _{termos cruzados} refere-se à energia de termos cruzados, que é responsável por fatores como distorções de ligações ou ângulos causadas por átomos próximos para reproduzir com precisão as propriedades dinâmicas das moléculas. E E _{não vinculado} refere-se à energia não ligada, que é responsável pelas interações entre átomos não ligados e resulta principalmente de interações de van der Waals (vdW) e interações eletrostáticas. Os três termos podem ser representados como
$$ \ begin {array} {c} {E} _ {\ mathrm {valence}} ={\ displaystyle \ sum_b \ left [{K} _2 {\ left (b- {b} _0 \ right)} ^ 2 + {K} _3 {\ left (b- {b} _0 \ right)} ^ 3+ {K} _4 {\ left (b- {b} _0 \ right)} ^ 4 \ right]} \\ {} \ kern2.5em + {\ displaystyle \ sum _ {\ theta} \ left [{H} _2 {\ left (\ theta - {\ theta} _0 \ right)} ^ 2+ {H} _3 {\ left (\ theta - {\ theta} _0 \ right)} ^ 3+ {H} _4 {\ left (\ theta - {\ theta} _0 \ right)} ^ 4 \ right]} \\ {} \ kern2.5em + {\ displaystyle \ sum _ {\ phi} \ left [{V} _1 \ left [1- \ cos \ left (\ phi - {\ phi} _1 ^ 0 \ right) \ right] + {V} _2 \ left [1- \ cos \ left (2 \ phi - {\ phi} _2 ^ 0 \ right) \ right] + {V} _3 \ left [1- \ cos \ left (3 \ phi - {\ phi} _3 ^ 0 \ right ) \ right] \ right]} \\ {} \ kern4.5em + {\ displaystyle \ sum _ {\ chi} {K} _ {\ chi} {\ chi} ^ 2 + {E} _ {\ mathrm {UB }}} \ end {array} $$ (2) $$ \ begin {array} {l} {E} _ {\ mathrm {cross} \ hbox {-} \ mathrm {term}} ={\ displaystyle \ sum_b {\ displaystyle \ sum_ {b ^ {\ prime}} {F} _ {b {b} ^ {\ prime}} \ left (b- {b} _0 \ right) \ left ({b} ^ {\ prime } - {b} _0 ^ {\ prime} \ right)}} \\ {} + {\ displaystyle \ sum _ {\ theta} {\ displaystyle \ sum _ {\ theta ^ {\ prime}} {F} _ {\ theta {\ theta} ^ {\ prime}} \ left (\ theta - {\ thet a} _0 \ right) \ left ({\ theta} ^ {\ prime} - {\ theta} _0 ^ {\ prime} \ right)}} + {\ displaystyle \ sum_b {\ displaystyle \ sum _ {\ theta} { F} _ {b \ theta} \ left (b- {b} _0 \ right) \ left (\ theta - {\ theta} _0 \ right)}} \\ {} + {\ displaystyle \ sum_b {\ displaystyle \ soma _ {\ phi} {F} _ {b \ phi} \ left (b- {b} _0 \ right) \ times}} \ left [{V} _1 \ cos \ phi + {V} _2 \ cos 2 \ phi + {V} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum_ {b ^ {\ prime}} {\ displaystyle \ sum _ {\ phi} {F} _ {b ^ {\ prime} \ phi} \ left ({b} ^ {\ prime} - {b} _0 ^ {\ prime} \ right) \ left ({b} ^ {\ prime} - {b} _0 ^ {\ prime} \ right) \ times}} \ left [{F} _1 \ cos \ phi + {F} _2 \ cos 2 \ phi + {F} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum _ {\ theta} {\ displaystyle \ sum _ {\ phi} {F} _ {\ theta \ phi} \ left (\ theta - {\ theta} _0 \ right) \ times}} \ left [{V} _1 \ cos \ phi + {V} _2 \ cos 2 \ phi + {V} _3 \ cos 3 \ phi \ right] \\ {} + {\ displaystyle \ sum _ {\ phi} {\ displaystyle \ sum _ {\ theta} { \ displaystyle \ sum _ {\ theta ^ {\ prime}} {K} _ {\ phi \ theta {\ theta} ^ {\ prime}} \ cos \ phi \ left (\ theta - {\ theta} _0 \ right) \ times \ left ({\ theta} ^ {\ prime} - {\ theta} _0 ^ {\ prime} \ right)}}} \ end {array} $$ (3) $$ {E} _ {\ mathrm {non} \ hbox {-} \ mathrm {bond}} ={\ displaystyle \ sum_ {i> j} \ left [\ frac { A_ {ij}} {r_ {ij} ^ 9} - \ frac {B_ {ij}} {r_ {ij} ^ 9} \ right]} + {\ displaystyle \ sum_ {i> j} \ frac {q_i { q} _j} {\ varepsilon {r} _ {ij}}} + {E} _ {\ mathrm {H} \ hbox {-} \ mathrm {bond}} $$ (4)
onde b e b ′ São os comprimentos de ligação de duas ligações adjacentes, e θ , ϕ e χ são o ângulo de duas ligações, o ângulo de torção diedro e o ângulo fora do plano, respectivamente. q é a carga atômica, ε é a constante dielétrica, r _ij é o i - j distância de separação atômica. b ₀ , K _i ( eu =2 - 4), θ ₀ , H _i ( eu =2 - 4), \ ({\ phi} _i ^ 0 \) ( i =1 - 3), V _i ( eu =1 - 3), \ ({F} _ {b {b} ^ {\ prime}} \), \ ({b} _0 ^ {\ prime} \), \ ({F} _ {\ theta { \ theta} ^ {\ prime}} \), \ ({\ theta} _0 ^ {\ prime} \), F _bθ , F _bϕ , \ ({F} _ {b ^ {\ prime} \ theta} \), F _i ( eu =1 - 3), F _θϕ , \ ({K} _ {\ phi \ theta {\ theta} ^ {\ prime}} \), A _ij e B _ij são ajustados a partir de cálculos da mecânica quântica e são implementados no módulo Discover do Materials Studio. O potencial de Lennard-Jones é empregado para descrever as interações intermoleculares entre moléculas de óleo, moléculas de óleo e nanocanais [14, 21, 22]. A distância de corte de 15,5 Å é selecionada para calcular as interações vdW, e o método de Ewald e o método baseado em átomos são aplicados para o cálculo das interações eletrostáticas e interações vdW, respectivamente. O sistema é calculado sob volume e temperatura constantes, ou seja, o conjunto NVT é empregado. A temperatura é de 298 K, e o método do termostato Andersen é escolhido para controlar o sistema em uma temperatura termodinâmica. A condição de limite periódica é imposta em todas as três dimensões. Os dados são coletados a cada 5 ps, e toda a trajetória precisa é registrada.

A principal composição de minerais de rocha é a sílica na maioria das formações de xisto [23,24,25]. Portanto, a superfície de sílica é selecionada como superfície de xisto betuminoso em nossa simulação. A estrutura inicial de sílica vem do banco de dados do software Material Studio. A superfície (0 0 1) é clivada e, em seguida, uma superfície retangular é refinada. As dimensões de cada superfície do substrato são 1,5 × 7 × 0,85 nm ³ . Um canal de separação ao longo do z - o eixo é criado entre as duas superfícies do substrato, conforme mostrado na Fig. 1a. As superfícies do canal são totalmente modificadas por hidroxila para representar as condições geológicas [26].

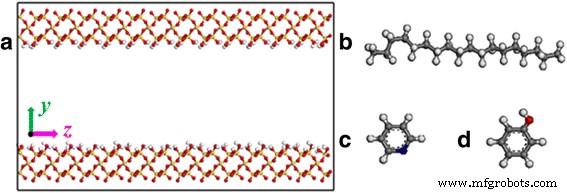
a Representação do modelo de nanocanal de sílica. Estruturas moleculares de b octadecano, c piridina e d fenol. Código de cores para átomos: vermelho , oxigênio; branco , hidrogênio; amarelo , silício; cinza , carbono; e azul , nitrogênio

A configuração inicial do sistema é construída por moléculas de octadecano que se acumulam dentro do canal de sílica. Quarenta moléculas de octadecano são inseridas no canal de fenda com uma largura de 2 nm, levando a uma densidade de 0,8 g / cm ³ . Também estudamos as propriedades de transporte das moléculas de piridina e fenol, outros dois componentes do óleo de xisto, para investigar o efeito das moléculas de óleo no transporte de óleo em nanocanais. As estruturas de octadecano, piridina e fenol são extraídas do banco de dados do software Material Studio, conforme mostrado na Fig. 1b – d. Para garantir uma densidade semelhante de óleo, o número de moléculas de piridina, moléculas de fenol e moléculas de octadecano em canais com larguras de 4 e 6 nm em nossas simulações são 407, 344, 80 e 120, respectivamente.

Usando o Discover Minimization, primeiro executamos a minimização de energia para otimizar o sistema para que ele fique bem equilibrado. As simulações de equilíbrio são realizadas usando uma pré-execução de 500 ps para garantir que o sistema atingiu um estado estacionário. Em seguida, simulações de não equilíbrio são realizadas aplicando uma força semelhante à gravidade paralela à superfície do canal (ao longo do z -eixo) para todas as moléculas de óleo, a fim de promover o transporte através de canais, que é comumente usado na simulação do transporte de fluidos [27,28,29]. Notamos aqui que uma limitação da simulação MD é que uma força comparável àquelas em configurações ambientais é impraticável, devido ao tempo necessário para cálculos MD; assim, aplicamos uma força que produz um valor médio de 3,1 × 10 ⁻¹⁴ N em cada átomo. A intenção da grande força é obter dados mais precisos para o transporte de petróleo em um tempo de simulação finito.

Resultados e discussão

Efeito da largura do canal

Primeiramente, prestamos atenção ao efeito da largura do canal nas propriedades de transporte do petróleo. Sob a ação da força externa, o número de átomos fluindo através da seção transversal do canal aumenta gradualmente com o tempo de simulação (Arquivo adicional 1:Figura S1, Informações de Apoio). As moléculas de óleo são puxadas por cerca de 2 ns. Conforme mostrado na Fig. 2d-f, com o incremento da largura do canal, a distância de deslocamento do óleo é maior após simulações de 2 ns MD. Para descrever quantitativamente o deslocamento do óleo ao longo do eixo do canal, calculamos o deslocamento COM do óleo entre sua localização inicial e a localização final após 2 ns. Simulações de MD e sua localização inicial ao longo do z -eixo e o centro de massa são definidos em termos de uma média ponderada de massa das coordenadas do átomo.

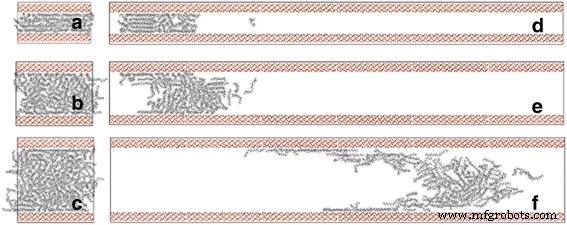
O modelo inicial do processo de transporte de moléculas de octadecano impulsionado por força em canais de sílica com larguras de a 2, b 4 e c 6 nm, e instantâneos de moléculas de octadecano em d 2, e 4, e f Canais de 6 nm a 2 ns
$$ {z} _ {\ mathrm {COM}} ={\ displaystyle \ sum_i \ frac {m_i} {M} {r} _i} $$ (5)
Na Fig. 3, apresentamos o deslocamento do óleo após simulações de 2 ns MD. Os resultados mostram que sob a condição de mesma força de tração em cada átomo, o deslocamento COM do óleo no canal de 2 nm é de apenas 0,85 nm, que é muito menor do que no canal de 6 nm. Isso sugere que o canal mais estreito fornece uma restrição de adsorção mais pronunciada nas moléculas de óleo.

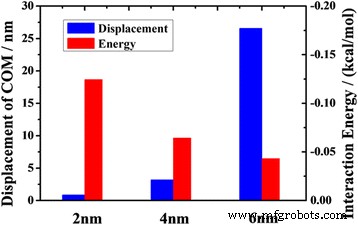
Os deslocamentos COM de óleo em 2 ns e energias de interação médias entre o óleo e o canal versus largura do canal

Para deixar claro o efeito da restrição de adsorção, calculamos a energia de interação média entre as moléculas de óleo e o substrato. A energia de interação média é calculada da seguinte forma:
$$ {E} _ {\ mathrm {média} \ \ mathrm {interação}} =\ frac {E _ {\ mathrm {total}} - \ left ({E} _ {\ mathrm {óleo}} + {E} _ {\ mathrm {substrato}} \ right)} {N} $$ (6)
onde E _{interação média} é a energia média de interação entre a molécula de óleo e o substrato; E _total representa a energia total de todo o sistema; E _óleo e E _substrato são a energia dos componentes do óleo e dos componentes do substrato, respectivamente; e N é o número total de átomos de moléculas de óleo [14, 30, 31]. A Figura 3 mostra que o deslocamento do óleo diminui com o aumento da energia média de interação. É óbvio que a adsorção entre as moléculas de óleo e o canal cresce com a energia de interação. A forte adsorção do canal inibe o transporte de óleo no canal estreito. A partir dos dados ilustrados na Fig. 3, descobrimos que quando a energia de interação é aumentada três vezes, o deslocamento do óleo diminui em mais de 30 vezes. Isso sugere que o transporte de óleo é muito influenciado pela interação entre a molécula de óleo e o substrato. No entanto, esse efeito diminui com o aumento da largura do canal. O efeito do tamanho no transporte de óleo é mais óbvio no nanocanal do que no microcanal (Arquivo adicional 1:Figura S2). Portanto, reduzir a energia de interação entre a molécula de óleo e o substrato é um fator chave para aumentar o transporte de óleo em nanocanais.

Pode ser visto na Fig. 2 que tem havido estruturas de estratificação óbvias perto da superfície do nanocanal, com uma espessura de aproximadamente 5 Å. Deve-se notar que a camada em contato com a superfície do canal e a camada no centro do canal são chamadas de camada de contato e camada central, respectivamente. Obviamente, camadas de moléculas de óleo bem ordenadas são encontradas na região próxima à superfície. A orientação das moléculas de octadecano é comumente caracterizada pelo ângulo θ entre o vetor normal para a superfície do canal e alguns vetores que são formados pela linha que conecta os dois átomos de carbono no final de uma molécula de octadecano [15, 29]. A distribuição de orientação para moléculas de octadecano em cada camada em 2 ns é apresentada na Fig. 4. Aqui, θ =80 ^o ∼ 90 ^o corresponde à orientação paralela da molécula, enquanto um valor de θ =0 ^o ∼ 10 ^o significa que a molécula é perpendicular à superfície do canal. Pode-se observar que as moléculas de octadecano são principalmente paralelas à superfície em camadas de canal de 2 nm e na camada de contato de canal de 4 nm e canal de 6 nm, devido à forte interação óleo-superfície (Fig. 5b). Para as camadas centrais do canal de 4 nm e do canal de 6 nm, não há orientação preferencial das moléculas de octadecano, o que significa que essas moléculas de octadecano tendem a se posicionar em vários ângulos em relação à superfície do canal. As moléculas de octadecano alinhadas na camada de contato podem ser importantes para as propriedades de transporte das moléculas de óleo em nanocanais.

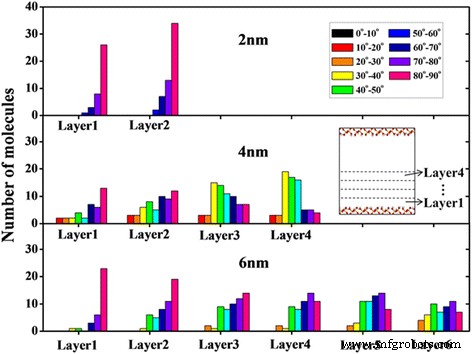
A distribuição do ângulo de orientação das moléculas de octadecano em cada camada para diferentes larguras de canal

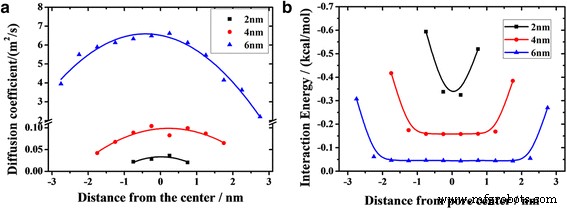
a Perfis de coeficiente de difusão de óleo em canais com larguras diferentes. b Dependência da distância da energia média de interação entre as moléculas de óleo e sílica (com símbolos). As linhas sólidas representam as funções de ajuste

A seguir, observamos que os tempos de inicialização (definidos como o tempo em que o deslocamento de uma camada é maior que 5 Å) para várias camadas são diferentes verificando as trajetórias. Os dados de tempo de inicialização listados nas informações de suporte (arquivo adicional 1:Tabela S1) mostram que o tempo de inicialização da camada de contato aumenta com a diminuição da largura do canal, o que significa que a força de tração necessária para iniciar o movimento de uma camada de contato em um canal mais estreito é maior do que o exigido em um canal mais amplo. Além disso, o tempo de inicialização da camada central é muito anterior ao da camada de contato.

Além disso, descobrimos que a taxa de fluxo de óleo diminui com o aumento da distância do eixo do canal, e a taxa de fluxo da camada de contato diminui com a diminuição da largura do canal (Fig. 2d-f). Para descrever quantitativamente esses caracteres, estudamos o coeficiente de difusão das moléculas de óleo em um local diferente do centro do canal, que é obtido a partir da evolução do tempo do deslocamento médio quadrático de acordo com
$$ D =\ frac {1} {4} \ underset {t \ to \ infty} {\ lim} \ frac {\ mathrm {d}} {\ mathrm {d} t} \ left \ langle {\ left | {r} _i (t) - {r} _i (0) \ right |} ^ 2 \ right \ rangle $$ (7)
onde r _i denota o vetor de posição de i a partícula e os colchetes angulares denotam uma média do conjunto. A Figura 5a mostra como os coeficientes de difusão das camadas dependem da posição no nanocanal. As curvas do canal de 4 nm e do canal de 6 nm apresentam um estilo parábola, ou seja, em direção à superfície do canal, os coeficientes de difusão das camadas diminuem gradualmente. O canal de 6 nm mostra a maior diferença entre o valor alto e o valor baixo de 4,4 m ² / s, enquanto o canal de 2 nm mantém a diferença mínima de 0,016 m ² / s. Os coeficientes de difusão das camadas no canal de 2 nm são ligeiramente diferentes, de modo que a superfície frontal do óleo se parece com um pistão. Além disso, descobrimos que os coeficientes de difusão das camadas na mesma distância da superfície do canal são bastante diferentes para vários canais (Fig. 5a). Por exemplo, o coeficiente de difusão da camada em contato com a superfície do canal inferior no canal de 6 nm é 3,9 m ² / s, enquanto que no canal de 2 nm é de apenas 0,02 m ² / s. Isso significa que a taxa de fluxo das camadas na mesma distância da superfície do canal aumenta com o aumento da largura do canal.

Na Fig. 5b, apresentamos a energia de interação média entre as moléculas de óleo em diferentes locais longe do centro do canal e do canal. As energias de interação são obviamente maiores em ambas as extremidades das curvas e diminuem rapidamente em 1 nm, pois o substrato tem forte adsorção em moléculas de óleo na faixa de 1 nm, e é uma das razões para o início lento das camadas de contato. No entanto, as energias de interação entre as moléculas de óleo e o canal não podem explicar adequadamente a forma da superfície frontal, pois seus valores para camadas fora da faixa de adsorção forte são quase os mesmos. A superfície frontal da parábola não está relacionada apenas à interação entre o óleo e o canal, mas também à interação entre as moléculas de óleo. A interação intermolecular contribui para a viscosidade do fluido, que desempenha um papel importante na transferência de momento no fluido viscoelástico. Como o intervalo de adsorção do canal no óleo é de cerca de 1 nm, algumas camadas estão localizadas na área, como estão marcadas por sombras na Fig. 6. As fortes interações superficiais entre o óleo e o substrato bloqueiam o transporte das camadas de óleo na sombra. O momentum é transferido das camadas da sombra para as camadas da sombra. O número de átomos fora da sombra diminui com a diminuição da largura do canal. Desse modo, menos momentum é transferido para as camadas de sombra no canal mais estreito. Assim, a velocidade de difusão da camada de contato diminui com a diminuição da largura do canal.

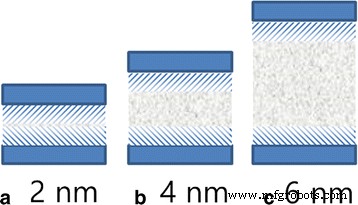
a , b , c Esquema da faixa de adsorção entre óleo e substrato

Efeito da Polaridade

O óleo de xisto sempre contém os componentes do óleo polar, e esses componentes do óleo polar desempenham um papel importante na adsorção da interface óleo / sílica [21, 32], portanto, entender seu impacto no transporte de óleo é crucialmente importante. Com fenol e piridina, por exemplo, realizamos simulações em um canal de 4 nm, e os números de átomos do fenol e da piridina são aproximadamente iguais ao número de átomos do octadecano no canal de 4 nm. Os instantâneos de piridina, fenol e octadecano no canal de sílica a 2 ns são mostrados na Fig. 7. Em comparação com as moléculas de octadecano, as moléculas de fenol e as moléculas de piridina quase não podem ser acionadas pela força de tração. A linha tracejada na Fig. 8 mostra os deslocamentos COM de diferentes moléculas de óleo após simulações de 2 ns MD. Embora as forças de tração em cada átomo sejam iguais, o deslocamento COM do octadecano é quase 16 vezes maior que o deslocamento COM do fenol e da piridina.

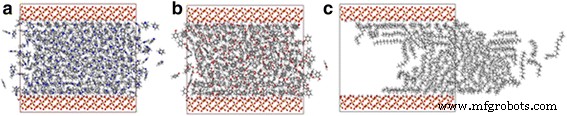
Instantâneos de a piridina, b fenol e c transporte de octadecano em canais de sílica de 4 nm a 2 ns

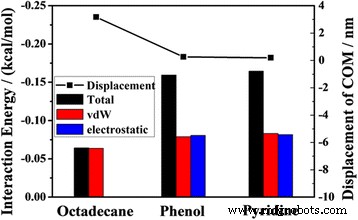
Os deslocamentos COM de óleo a 2 ns e energias de interação médias (total, vdW e eletrostática) entre os diferentes componentes e o canal

Para entender esses resultados, calculamos a energia da interação total, interação vdW e interação eletrostática entre os diferentes componentes e o canal. O histograma da Fig. 8 ilustra que a energia total de interação entre o fenol (piridina) e o substrato de sílica é maior do que entre o octadecano e o canal de sílica. Como a molécula de octadecano é uma molécula de cadeia não polar, a interação total entre as moléculas de octadecano e o canal resulta principalmente da interação vdW, e há pouca interação eletrostática, enquanto as contribuições da interação vdW e interação eletrostática entre fenol (piridina) e o canal para a interação total são quase iguais.

Para investigar a influência da polaridade no transporte de óleo, calculamos o momento de dipolo das três moléculas usando a simulação do primeiro princípio. Os detalhes de desempenho seguem nosso trabalho anterior [33,34,35,36]. Os resultados mostram que os momentos de dipolo de octadecano, fenol e piridina são 0,0322, 1,3059 e 2,2449 Debye, respectivamente. Isso indica que as moléculas de óleo polar são muito mais difíceis de serem acionadas do que as moléculas não polares em nanocanais. Mas o deslocamento COM do óleo nem sempre aumenta com a diminuição da polaridade. Para as duas moléculas de óleo polares, a polaridade do fenol é mais fraca do que a polaridade da piridina, mas os deslocamentos COM delas são quase iguais.

Efeito dos tipos de materiais

Os caracteres de transporte das moléculas de óleo também são comparados entre os nanocanais fabricados a partir de vários tipos de materiais, incluindo sílica, ouro e calcita. A Figura 9 mostra os instantâneos de moléculas de octadecano em canais de calcita e ouro em 2 ns. A Figura 9a mostra um transporte distinto de moléculas de óleo no canal de calcita, indicando que as moléculas de octadecano na calcita também podem ser impulsionadas pela força de tração, enquanto as moléculas no canal de ouro dificilmente podem se mover (Fig. 9b).

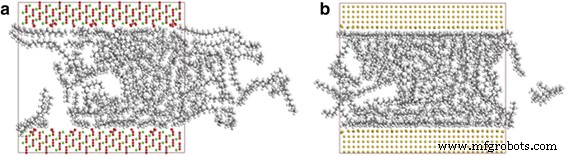
Instantâneos do transporte de octadecano em 4 nm a canal de calcita e b canal de ouro em 2 ns. Código de cores para átomos:verde, cálcio; ouro amarelo

A Figura 10 mostra os deslocamentos COM das moléculas de octadecano em canais de vários materiais e as energias de interação médias entre o óleo e os diferentes canais de materiais. O deslocamento COM do óleo no canal de sílica é muito maior do que no canal de ouro. O fenômeno pode ser explicado pelo efeito da interação entre as moléculas de óleo e o canal. A interação média é muito menor entre as moléculas de óleo e o canal de sílica do que entre as moléculas de óleo e o canal de ouro. Mas para o transporte das moléculas de óleo no canal de sílica e no canal de calcita, esse fator não pode explicar adequadamente a diferença. A energia média de interação entre as moléculas de óleo e o canal de sílica não parece ser muito diferente daquela entre as moléculas de óleo e o canal de calcita, mas os deslocamentos COM nos dois casos são bastante diferentes. A razão pode estar relacionada aos átomos da superfície e à textura da superfície. Esses resultados indicam que o transporte do óleo é muito influenciado pela interação entre as moléculas do óleo e o canal, mas quando os valores da energia de interação são semelhantes, o transporte do óleo em nanocanal é a competição entre esses fatores.

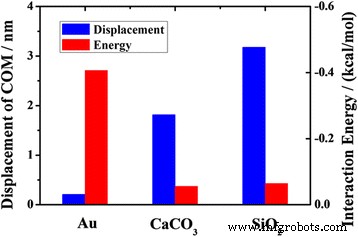
Os deslocamentos COM do óleo a 2 ns e as energias médias de interação entre o óleo e substratos de diferentes materiais

Efeito da rugosidade da superfície

Como é bem sabido, a rugosidade da superfície nanométrica tem pouca influência nos fluxos de fluidos dentro dos canais micrométricos. No entanto, foi demonstrado que a rugosidade da superfície nanométrica tem grande influência no transporte de fluidos em nanocanais [37,38,39]. Para investigar o efeito da rugosidade no transporte de octadecano, construímos superfícies rugosas cortando uma pequena quantidade de átomos da superfície do substrato, de modo que uma cavidade com uma profundidade de d =3 Å (ou 6 Å) e uma largura de 35 Å é formada na superfície do substrato. Os átomos nus de oxigênio foram modificados por átomos de hidrogênio. Cinco e dez moléculas de octadecano são adicionadas à cavidade de 3 Å e cavidade de 6 Å, respectivamente, e a força externa é aumentada correspondentemente. A Figura 11 mostra a comparação de instantâneos para octadecano fluindo através de um canal irregular com profundidades de cavidade de 3 e 6 Å a 2 ns. We observe that inside every cavity, there are some oil molecules, and their localizations are affected by the cavity, which results in a reduction of velocity values inside the cavity, as well as the velocity of oil molecules nearby. And this becomes more obvious when d  = 6 Å, as shown in Fig. 11b. To quantify the influence of roughness on transportation, we further calculate the COM displacement of oil in rough channels. The COM displacements of oil in channels with 3 and 6 Å depth cavity are 3.95 and 3.07 Å, respectively. When d  = 6 Å, the value of oil displacement is 3.07 Å, which is smaller than the value 3.17 Å of oil molecules in flat channel. Somewhat surprisingly, however, for d  = 3 Å, the displacement is even larger than that in flat channel. We expect that these characters are contributed by two parts:(1) the cavity increases the width of the nanochannel so that the oil molecules have a greater diffusion coefficient according to the above discussion, which facilitates the transportation of oil; (2) the oil molecules in cavity can suppress the transportation of oil molecules nearby and therefore decrease the oil transportation speed. For the oil molecules in channel with d  = 3 Å, the effect of suppression caused by the less oil molecules in cavity is less than the effect of facilitation caused by the width increment. When d  = 6 Å, the diffusion coefficient of oil molecules is further increased; however, more oil molecules are suppressed by the deeper cavity, and the effect of suppression on the transportation of oil molecules is more than that of facilitation, thereby reducing the oil displacement. Because of these complications, we cannot separate these parts and judge how much contribution of each part has on the displacement.

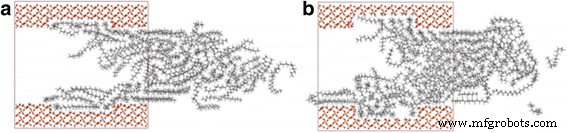
Snapshots of octadecane transportation in rough channel with the cavity depth of a 3 and b 6 Å at 2 ns

Conclusions

In this study, we investigate the mechanism of oil transportation in nanochannels using molecular dynamics simulations. It is demonstrated that the oil displacement in a 6 nm channel is over 30 times larger than that in a 2 nm channel, and the diffusion coefficient of oil molecules at the center of the 6 nm channel is almost two times more than that near the channel surface, due to interaction difference between the oil molecules and channels. Besides, we find that both the polarity of oil molecules and channel component have great effects on the interaction between oil molecules and channel in the channels with same width; the larger the interaction between oil molecules and channel is, the smaller the oil displacement is. Finally, we demonstrate that surface roughness can obviously affect oil transportation in nanochannels. The mechanism by which the cavity structure affects the transportation of oil is an intricate issue, which should be further studied. Our findings would contribute to revealing the mechanism of oil transportation in nanochannels and therefore are very important for design of oil extraction in nanochannels.

Abreviações

COM:

Center of mass

COMPASS:

Condensed-phase optimized molecular potential for atomistic simulation studies

MD:

Molecular dynamics

vdW:

van der Waals

Nanotécnicas Inativam células-tronco cancerosas NiCo2S4 @ NiMoO4 Core-Shell Heterostructure Nanotube Arrays cultivados em Ni Foam como um eletrodo livre de aglutinante exibiu alto desempenho eletroquímico com alta capacidade