Propriedades elétricas de materiais compostos com alinhamento assistido por campo elétrico de cargas de nanocarbono

Resumo

O artigo relata o alinhamento das nanopartículas de carbono induzidas por campo elétrico em matriz epóxi. A microscopia óptica foi realizada para considerar o efeito da magnitude e configuração do campo elétrico, morfologia do preenchimento e razão de aspecto no processo de alinhamento. O tempo característico de formação da rede alinhada foi comparado com as previsões de modelagem. O tempo de rotação de nanotubos de carbono e nanoplacas de grafite foi estimado usando um modelo analítico baseado na abordagem de meio efetivo. Diferentes fatores de despolarização foram aplicados de acordo com as geometrias da partícula e do campo elétrico.

Nanocompósitos sólidos foram fabricados usando campo elétrico AC. Nós investigamos a dependência da concentração da condutividade elétrica de nanoplacas de grafite / compósitos de epóxi usando a técnica de duas sondas. Foi estabelecido que as propriedades elétricas de compósitos com distribuição aleatória e alinhada de filler diferem pelo valor de condutividade em determinado conteúdo de filler e se distinguem por uma forma de dependência da concentração da condutividade para fillers com morfologia diferente. Essas diferenças foram explicadas em termos de percolação dinâmica e formação de várias redes condutoras:encadeadas no caso de nanoplacas de grafite e arcabouço cruzado no caso de nanotubos de carbono filler.

Histórico

Propriedades adaptáveis fornecem uma aplicação de materiais compósitos à base de carbono condutores em muitas indústrias como componentes eletrônicos e de construção:em microeletrônica, dissipação eletrostática, na fabricação de escudos eletromagnéticos, para estruturas de aeronaves, etc. [1,2,3,4]. Eles não corroem como os metais, mas possuem resistência, peso e ampla faixa de valores de condutividade apropriados devido a uma variedade de cargas empregadas.

Partículas não esféricas são mais favoráveis como cargas compostas do ponto de vista de melhorar a condutividade elétrica do composto [5,6,7]. Isso se deve aos menores valores do fator de empacotamento no aumento da razão de aspecto das partículas [8], que é um parâmetro do modelo estatístico de percolação. Portanto, o desenvolvimento de compósitos com nanotubos de carbono (CNTs) e nanoplacas de grafite (GNPs), que são caracterizados por altos valores de relação de aspecto (10 ¹ –10 ⁴ ) [9], como preenchedores, é uma direção muito promissora. Além da anisotropia geométrica, os CNTs e os GNPs se distinguem pela anisotropia de propriedades físicas. Mas, na distribuição aleatória do enchimento no composto, a anisotropia da partícula de enchimento individual é compensada. Além disso, na distribuição de preenchimento aleatório, muito dele está concentrado nas chamadas ramificações “em branco” de uma rede condutiva que são disjuntas da rede geral. Essas perdas são particularmente consideráveis com baixo teor de carga no compósito.

A recomposição do filler e sua distribuição espacial específica permitem a obtenção de compósitos com baixo limiar de percolação o que reduz o custo do material. Os métodos mais populares de preparação de compósitos com distribuição de carga anisotrópica são a exposição da mistura de compósitos líquidos ao campo eletromagnético e a aplicação de tensões mecânicas. Dentre as desvantagens do método de alinhamento do filler por laminação, a tensão de cisalhamento é a possível quebra e destruição das nanopartículas de carbono sob tal exposição [10]. O alinhamento induzido pelo campo magnético requer a adição de componentes magnéticos ao compósito [11]. Assim, o alinhamento assistido por campo elétrico do enchimento em compósito é o método mais promissor de formação de compósito anisotrópico do ponto de vista de muitos grupos de pesquisa [12, 13].

Mas a grande maioria dos trabalhos apresentados sobre alinhamento assistido por campo elétrico é dedicada a nanotubos de carbono embutidos em matriz polimérica [14,15,16,17,18]. O efeito da morfologia das partículas de carga sobre o processo de alinhamento é muito pouco desenvolvido tanto em estudos teóricos quanto experimentais [19,20,21]. O objetivo deste estudo foi investigar a influência da morfologia do filler no processo de formação de compósitos alinhados e identificar e explicar as diferenças de dependência da concentração da condutividade elétrica dos compósitos com distribuição aleatória e alinhada do PNB.

Métodos

Materiais

Com base na resina epóxi Larit 285 (Lange Ritter GmbH, Alemanha), materiais compósitos foram fabricados e investigados neste estudo. No estado inicial, este polímero é de dois componentes e consiste em epóxi líquido e endurecedor H 285 apropriado. Baixa viscosidade da resina usada (600 ÷ 900 mPa × s a 25 ° С) e endurecedor (50 ÷ 100 mPa × s em 25 ° С) permite usar o impacto de um campo elétrico externo para a fabricação de materiais compostos em sua base.

Os seguintes materiais foram usados como enchimentos para os sistemas compostos fabricados:

Nanotubos de carbono de parede múltipla (MWCNTs) (Cheap Tubes Ins, EUA);
Nanoplacas de grafite (GNPs).

Os GNPs foram obtidos por dispersão ultrassônica (em meio de acetona por 3 h) de grafite esfoliada termicamente, que é um produto resultante do tratamento termoquímico profundo da grafita dispersa. O processo de fabricação do GNP é descrito em detalhes em [22].

A Tabela 1 contém os parâmetros dos enchimentos usados. Suas dimensões e forma foram estimadas usando AFM, SEM e microscopia óptica em artigos de nosso grupo de pesquisa [23, 24]. Partículas GNP e MWCNT distinguem-se pela forma, tamanho e, portanto, uma razão de aspecto. A Tabela 1 contém parâmetros característicos para as partículas maiores, menores e médias. As partículas são marcadas como “max”, “min” e “aver” pelos valores de sua proporção de aspecto. A avaliação da massa das partículas sugeriu que a densidade ρ (MWCNT) =1,8 g / cm ³ [25], ρ (GNPs) =2,23 g / cm ³ , como a densidade da grafite monocristalina.

Fabricação composta

As amostras compostas que foram preparadas continham diferentes concentrações de GNPs como enchimento (0,05, 0,5, 0,7, 1, 2, 3, 4, 5% em peso). Um tipo de amostra teve distribuição aleatória do preenchedor e, em outro, os PNB foram alinhados por campo elétrico externo.

O método de preparação de sistemas compostos foi o seguinte. No início, a quantidade necessária de enchimento de carbono foi vertida na matriz de polímero pré-dissolvido e misturada mecanicamente. Em seguida, a mistura foi exposta à dispersão ultrassônica para melhor distribuição do filler em matriz epóxi. A dispersão foi realizada em banho ultrassônico Вaku-9050 com frequência de 40 kHz e potência elétrica de saída máxima de 50 W. A mistura composta foi exposta à ação ultrassônica por 30 min a 50 W, após o endurecedor Í 285 ter sido adicionado ao composto resultante mistura na proporção de 100/40 em massa para o peso de Larit 285.

Eventualmente, para compósitos com fabricação de distribuição de enchimento alinhada, uma parte da mistura de compósitos obtida foi despejada em um molde de plástico que foi colocado entre as placas do capacitor. Tensão AC com frequência de 15 kHz e magnitude de 2.000 V foi aplicada às placas. Fonte de alta tensão com a capacidade de gerar tensão CA na freqüência de 15 kHz e magnitude na faixa de até 2.000 V ou tensão CC com magnitude na faixa de até 2.000 V foi utilizada como fonte de campo elétrico. O valor da magnitude do campo elétrico foi controlado por voltímetro universal В7-16А.

Ao escolher a frequência do campo elétrico CA, tivemos em mente dois pontos:(1) a frequência deve ser alta o suficiente para que o tempo de alinhamento das nanopartículas de carbono seja o tempo de endurecimento do epóxi; (2) a frequência deve ser baixa o suficiente para observar a dinâmica do alinhamento das nanopartículas no campo elétrico. Tendo em vista essas considerações, realizamos a formação dos compósitos na freqüência de 15 kHz.

A outra parte da mistura composta foi deixada sem a influência de um campo elétrico externo.

Depois de mantidos em temperatura ambiente, os moldes com amostras compostas foram submetidos a tratamento térmico em temperatura crescente de 40 a 80 ° C, que aumentou em 10 ° C de hora em hora. Isso foi feito para completar o processo de polimerização dos compósitos.

Microscopia óptica

A investigação do caráter da distribuição de cargas de carbono em matriz epóxi sob tratamento de campo elétrico foi realizada para compósitos com teor de carga de carbono de 0,05% em peso. Isso foi feito com um microscópio óptico estereoscópico МBS-1 equipado com câmera digital Etrek DCM-510. Esta configuração proporcionou a oportunidade de observação online do epóxi líquido com nanopartículas de carbono dispersas sob a influência do campo elétrico. A configuração do experimento é descrita em detalhes em [26, 27]. Uma série de observações ópticas dos compósitos MWCNTs / - e GNPs / Larit 285 foi conduzida em tempo real fornecendo eletrodos com tensão CA de 15 kHz ou tensão CC e alterando o valor da magnitude do campo elétrico.

Medição de propriedades elétricas

A condutividade elétrica dos compósitos investigados foi medida pelo método padrão de duas sondas no modo DC à temperatura ambiente com um limite de medição da resistência elétrica de 10 ¹⁰ ohm. Mais de 10 ¹⁰ ohm, as resistências foram medidas usando teraommetr Е6–13. As amostras para as medições foram preparadas na forma de paralelepípedos regulares com as dimensões 5,0 × 4,0 × 4,0 mm ³ .

Modelagem

Equações pelas quais o tempo característico de rotação das partículas de carbono sob a ação do campo elétrico foi estimado foram resolvidas usando um pacote matemático Maple 13.

Resultados e discussão

Observações ópticas

As figuras a seguir mostram fotos ópticas da superfície de materiais compósitos GNPs / Larit 285 (Figs. 1 e 2) e MWCNTs / Larit 285 (Figs. 3 e 4) [26] de baixo teor de enchimento (0,05% em peso) na ação de campo elétrico AC.

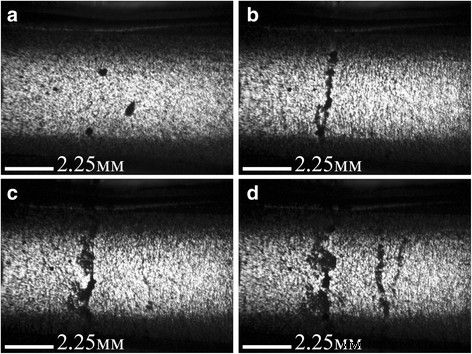
Imagens ópticas de formação de "colapso elétrico" em 0,05% em peso de GNPs / composto Larit 285 sob ação de campo elétrico CA de força de 36 kV / m, frequência de 15 kHz (eletrodos embutidos): a —Antes da ação do campo elétrico; b —Após 100 s; c —Após 140 s; d —Após 160 s de ação do campo elétrico. Tamanho da imagem 10,8 × 8,0 mm ²

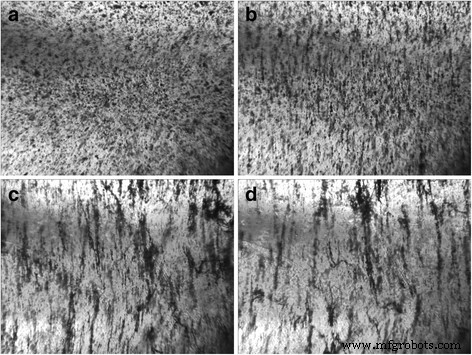
Imagens ópticas de 0,05% em peso de GNPs / composto Larit 285 sob a ação do campo elétrico CA (frequência de 15 kHz, força de 167 kV / m) (no capacitor): а— antes da ação do campo elétrico; b —Após 12 min; c —Após 26 min; d —Após 60 min de ação do campo elétrico. Tamanho da imagem 10,8 × 8,0 mm ²

Imagens ópticas de 0,05% em peso do composto MWCNTs / Larit 285 sob a ação do campo elétrico CA (frequência de 15 kHz, força de 83,3 kV / m) (eletrodos embutidos): a - antes da ação do campo elétrico; b - após 12 min; c - após 26 min; d - após 60 min de ação do campo elétrico. Tamanho da imagem 10,8 × 8,0 mm ² [26]

Imagens ópticas de 0,05% em peso do composto MWCNTs / Larit 285 sob a ação do campo elétrico CA (frequência de 15 kHz, força de 50 kV / m) (eletrodos embutidos): а —Antes da ação do campo elétrico; b —Após 12 min; c —Após 26 min; d —Após 60 min de ação do campo elétrico. Tamanho da imagem 10,8 × 8,0 mm ² [26]

Processados com campo elétrico CA, os compostos tornam-se mais transparentes com o aumento do tempo de ação do campo elétrico devido ao movimento do preenchedor na direção das linhas de força de um campo elétrico externo. Observou-se também que com o aumento do tempo de ação do campo elétrico, as estruturas alinhadas da carga de carbono se alargam e surgem algumas folgas entre elas. Isso pode ser devido às interações de Van der Waals de nanopartículas de carbono. Desta forma, cadeias de carga de nanocarbono de distribuição especificada estão se formando em compósito.

Como visto na Fig. 1, para compósitos GNPs / Larit 285 na configuração de eletrodos embutidos, a ação do campo elétrico CA se manifesta na criação do caminho condutor principal, que fecha o fornecimento com eletrodos de tensão externos e leva a um fluxo de corrente de alta amplitude através do amostra composta. Portanto, o alinhamento dos GNPs no Larit 285 foi realizado pelo conjunto experimental quando o compósito é colocado entre as placas do capacitor. A Figura 2 mostra que tal configuração de arranjo experimental em que o fluxo de corrente através da amostra é impossível permite a obtenção de cadeias consistentemente alinhadas de GNPs em matriz polimérica.

No caso do tratamento dos compósitos MWCNTs / Larit 285 com campo elétrico CA, também foi observada uma formação de alongamento na direção das cadeias do campo elétrico. Cadeias distintas tornam-se mais espessas quando o tempo de exposição ao campo CA aumenta. Mas o tempo característico de formação de cadeia alinhada em MWCNTs / compósito epóxi é de minutos, enquanto em GNPs / compósito epóxi é de segundos na configuração de eletrodos embutidos. Além disso, devido à forma e ao tamanho do GNP, a distribuição alinhada do enchimento em GNPs / compósitos epóxi pode ser formada em menores magnitudes de campo elétrico CA do que em MWCNTs / compósitos epóxi. Mas, por outro lado, devido à mobilidade dos GNPs por causa de sua forma e tamanho em comparação com MWCNTs, a formação de compósitos a granel com enchimento de GNP é complicada. A rede alinhada de GNPs tende a se destruir logo após desligar o campo elétrico se o composto não tiver polimerizado completamente.

Ao considerar todas as imagens ópticas da rede alinhada sob a formação do campo elétrico AC em GNPs / - e MWCNTs / compósitos epóxi, podemos concluir que em igualdade de condições ao mudar apenas o tipo de carga de carbono, a rede alinhada é formada mais rapidamente nos GNPs / epóxi composto. No caso dos MWCNTs, sua tendência à aglomeração impede o alinhamento efetivo na direção do campo elétrico aplicado. Deve-se notar que o campo DC não é eficaz para a formação de redes alinhadas em composto [26].

Para explicar a observação por microscopia óptica das peculiaridades do alinhamento assistido por campo elétrico do enchimento de diferentes morfologias, um tempo característico de rotação de nanopartículas de carbono em matriz epóxi sob ação de campo elétrico AC foi estimado teoricamente.

Modelagem do alinhamento de partículas de carbono em meio viscoso

O mecanismo do compósito com uma distribuição espacial especificada do método de formação de preenchimento é que cada nanopartícula de carbono que está embutida na matriz dielétrica sofre polarização sob a ação do campo elétrico AC devido à polarização da interface entre o polímero e a partícula. Geralmente, o momento de polarização e o vetor do campo elétrico são não colineares devido à anisotropia das nanopartículas. Portanto, quando o campo elétrico é ativado, ocorre um torque que leva à rotação das nanopartículas de carbono na direção do campo. Sabe-se que o movimento de rotação de uma partícula, neste caso, é descrito pela seguinte equação [16]:
$$ I \ frac {d ^ 2 \ varTheta} {dt ^ 2} + {T} _ {\ eta} + {T} _ {\ mathrm {align}} =0 $$ (1)
onde eu é o momento de inércia da nanopartícula de carbono; Θ é o ângulo entre a direção da partícula e do campo elétrico; T _η é um torque de amortecimento; \ ({T} _ {\ mathrm {align}} \ approx \ left [\ overrightarrow {\ mu} \ times \ overrightarrow {E} \ right] \) é o torque induzido pelo campo; \ (\ overrightarrow {\ mu} =f \ left (\ varepsilon, {\ sigma} _1, {\ sigma} _2, v \ right) \) é o momento de polarização que depende dos valores da constante dielétrica ( ε ) e condutividade ( σ ₁ , σ ₂ ) de nanopartículas e matriz; v = f ( m , l , d ) é o volume da nanopartícula de carbono que depende do seu peso ( m ) e dimensões ( l , d )

Geralmente, o momento de polarização \ (\ overrightarrow {\ mu} \) é proporcional ao campo externo \ (\ overrightarrow {E} \) e ao volume da partícula ν e é determinado pela fórmula [28]:
$$ \ overrightarrow {\ mu} ={\ varepsilon} _0 {\ varepsilon} _m \ beta \ nu \ overrightarrow {E} $$
onde ε ₀ é a permissividade do espaço livre, ε _m é uma constante dielétrica da matriz, β é um parâmetro adimensional que, em particular, depende da forma de inclusão. Em [28], fórmulas de β para um disco condutivo ideal e cilindro são dados:
$$ {\ beta} _ {\ perp} ^ {\ mathrm {disco}} =\ frac {\ sigma_p - {\ sigma} _m} {\ sigma_p}, \ kern1em {\ beta} _ {II} ^ {\ mathrm {disco}} =\ frac {\ sigma_p - {\ sigma} _m} {\ sigma_m}; $$ $$ {\ beta} _ {\ perp} ^ {\ mathrm {cilindro}} =\ frac {2 \ left ({\ sigma} _p - {\ sigma} _m \ right)} {\ sigma_p + {\ sigma } _m}, \ kern1em {\ beta} _ {II} ^ {\ mathrm {cilindro}} =\ frac {\ sigma_p - {\ sigma} _m} {\ sigma_m}. $$
Conclui-se dessas dependências que \ ({\ overrightarrow {\ mu}} _ {II} \ ne {\ overrightarrow {\ mu}} _ {\ perp} \) ( II significa co-direção do eixo longo da partícula e da direção do campo, ⊥ - perpendicularidade). Assim, para GNPs e MWCNTs, \ ({\ overrightarrow {\ mu}} _ {II}> {\ overrightarrow {\ mu}} _ {\ perp} \) por causa de sua forma e propriedades.

Para avaliar o tempo característico de rotação das partículas de carbono sob a ação do campo elétrico e seu alinhamento pela direção do campo Eq. (1) com as condições iniciais Θ ( t =0) = Θ ₀ , \ (\ frac {d \ varTheta} {dt} \ left (t =0 \ right) =0 \) foram resolvidos. De acordo com [16], os termos na equação principal do movimento são os seguintes:
$$ {T} _ {\ eta} =8 \ pi \ eta \ nu \ frac {d \ varTheta} {dt}, $$ $$ {T} _ {\ mathrm {align}} =\ frac {1} {4} {\ nu \ varepsilon} _m \ operatorname {Re} \ left [{\ alpha} ^ {\ ast} \ right] {E} ^ 2 Sin2 \ varTheta, \ pm $$
onde \ ({\ alpha} ^ {\ ast} =\ left ({\ left ({\ varepsilon} _p ^ {\ ast} - {\ varejpsilon} _m ^ {\ ast} \ right)} ^ 2 \ right) / \ left (\ left [{\ varepsilon} _m ^ {\ ast} + \ left ({\ varepsilon} _p ^ {\ ast} - {\ varepsilon} _m ^ {\ ast} \ right) {L} _x \ direita] \ left ({\ varepsilon} _p ^ {\ ast} + {\ varepsilon} _m ^ {\ ast} \ right) \ right) \) é uma polarizabilidade, \ ({\ varepsilon} _ {m, p} ^ {\ ast} ={\ varepsilon} _ {m, p} -j \ frac {\ sigma_ {m, p}} {\ omega} \), e ε _{m , p} , σ _{m , p} são a constante dielétrica e a condutividade do meio e da partícula, ω =2 πf , f —Frequência do campo elétrico.

Para determinar o fator de despolarização do nanotubo de carbono e da nanoplaca de grafite, eles devem ser considerados como as partículas de determinada forma (Fig. 5). MWCNT pode ser considerado apenas como elipsóide. A elipticidade do MWCNT na aproximação do elipsóide é \ (e =\ sqrt {1 - {\ left (2 {r} _0 / l \ right)} ^ 2} \). O PNB pode ser considerado esferóide ou elipsóide. A elipticidade do GNP na aproximação elipsóide é \ (e =\ sqrt {1 - {\ left (h / 2R \ right)} ^ 2} \) e na aproximação esferóide é \ (e =\ left (2R / h \ direita) \ sqrt {1 - {\ left (h / 2R \ right)} ^ 2} \). Então as expressões do fator de despolarização assumem a seguinte forma [28].

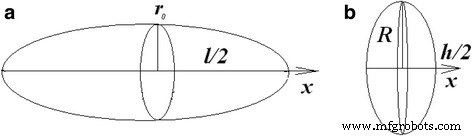
Imagens esquemáticas de nanotubo de carbono ( a ) e nanoplaqueta de grafite ( b )

Para o elipsóide:
$$ {L} _x =\ frac {1- {e} ^ 2} {e ^ 3} \ left (Arth \ kern0.5em e-e \ right). $$
Para o esferóide:
$$ {L} _x =\ frac {1+ {e} ^ 2} {e ^ 3} \ left (e- \ arctan \ kern0.5em e \ right), \ kern2.5em {L} _x + 2 { L} _R =1. $$
Nas equações acima, L _x é um fator de despolarização se o campo externo for aplicado ao longo do x -eixo (como na Fig. 5), L _R é um fator de despolarização se o campo externo for aplicado ao longo do raio do PNB.

Gastando os fatores de despolarização em série, as expressões acima assumem a seguinte forma.

Para o elipsoidal MWCNT:
$$ {L} _x =\ frac {4 {r} _0 ^ 2} {l ^ 2} \ left [\ ln \ left (\ frac {l} {r_0} \ right) -1 \ right] $$ ( 2)
Para o PNB elipsoidal:
$$ {L} _x =\ frac {h ^ 2} {4 {R} ^ 2} \ left [\ ln \ left (\ frac {4R} {h} \ right) -1 \ right] $$ (3 )
Para PNB esférico:
$$ {L} _x \ approx 1- \ frac {h \ left (8 \ pi {R} ^ 2-16hR + 3 \ pi {h} ^ 2 \ right)} {32 {R} ^ 3} $$ (4) $$ {L} _R \ approx \ frac {h \ left (8 \ pi {R} ^ 2-16hR + 3 \ pi {h} ^ 2 \ right)} {64 {R} ^ 3} $ $ (5)
Além disso, para destacar as peculiaridades da morfologia das partículas, o volume do CNT foi solicitado como o volume de um cilindro oco \ (\ nu =\ pi l \ left ({r} _0 ^ 2- {r} _i ^ 2 \ right) \ ), enquanto o volume GNP foi perguntado como o volume de um disco ν = πR ² h .

O momento de inércia do nanotubo de carbono foi tomado como \ (I =\ frac {ml ^ 2} {12} \) - o momento de inércia da haste reta fina com o comprimento de l e massa de m , o eixo de rotação é perpendicular à haste e passa por seu centro de massa. O momento de inércia da nanoplaca de grafite foi tomado como \ (I =\ frac {mR ^ 2} {2} \) - o momento de inércia do disco, o raio do qual é R , e massa de m , o disco está girando em torno da perpendicular ao seu eixo plano.

Em seguida, usando toda a abordagem anterior e definindo parâmetros numéricos, cálculos da mudança do ângulo de inclinação de partículas de morfologia diferente em relação à direção do campo com o tempo de tratamento do campo elétrico AC foram realizados.

Baseando-se em papel [29] onde as dependências experimentais da concentração de partes reais e complexas da permissividade dielétrica dos compósitos com grafite fina e nanotubos de carbono foram descritas pela fórmula e equações de Nielsen.
$$ {\ varejpsilon} _ {CNT} ^ {\ ast} =62,2 \ hbox {-} 12,4 \ vezes i, \ kern1em {\ varepsilon} _c ^ {\ ast} =34,3 \ hbox {-} 13,4 \ vezes eu $$
são dados, em nossos cálculos para o PNB ε _{p ( PNB )} =34,3, e para MWCNT, ε _{p ( CNT )} =62,2 foi obtido.

Os parâmetros geométricos das partículas foram retirados da Tabela 1. Em relação aos outros parâmetros numéricos usados, foi colocado que ε ₀ =8,85 × 10 ⁻¹² F / m, η =0,75 Pa × s, f =15 kHz, ε _m =2.8 ε ₀ [30], σ _m =10 ⁻⁶ Sm / m [16]. A condutividade de partículas individuais de carbono foi considerada como σ _{p ( CNT )} =10 ⁵ Sm / m [31], σ _{p ( PNB )} =10 ⁵ Sm / m [32, 33] _.

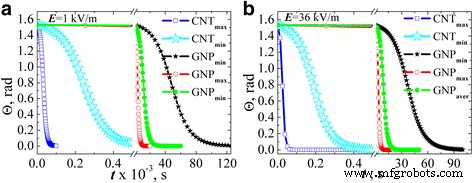
A Figura 6 mostra o ângulo de inclinação da partícula em relação à direção da dependência do campo aplicado do tempo de ação do campo quando L _x foi avaliada pelas Eqs. (2) e (3). Os resultados foram encontrados para dois valores de intensidade de campo:1 kV / m (Fig. 6а) e 36 kV / m (Fig. 6b) supondo que a partícula esteja quase completamente desordenada no momento inicial ( Θ ( t =0) = π / 2.05).

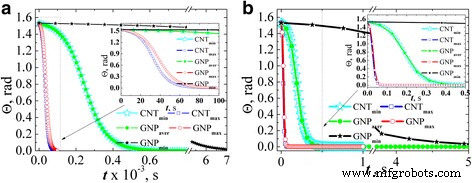
A evolução do ângulo de inclinação das partículas de enchimento de carbono em relação à direção do campo estimada em elipsóides aproximados para a intensidade do campo elétrico AC 1 kV / m ( a ) e 36 kV / m ( b )

Houve uma correlação clara entre a relação de aspecto das partículas e o tempo de alinhamento pelo campo elétrico. Ou seja, o tempo máximo para o alinhamento é para partículas com a razão de aspecto mais baixa (GNP _min ) Para GNP _max e CNT _max , o tempo de alinhamento é quase igual, e o tempo igual de alinhamento é para GNP _aver e CNT _min .

A Figura 7 mostra os valores do fator de despolarização que foram estimados pelas Eqs. (2) e (3) para GNPs e MWCNTs. L _x é um fator geométrico e não depende dos valores absolutos dos semi-eixos dos elipsóides simulados, mas de sua proporção. Assim, L _x é uma função direta da proporção de aspecto da partícula.

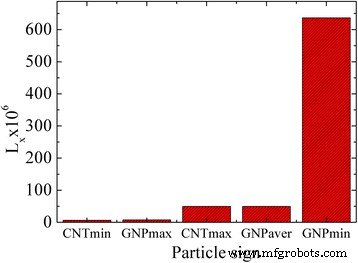
Fator de despolarização para GNPs e MWCNTs avaliados pelas Eqs. (2) e (3)

Ou seja, o fator de despolarização é o principal parâmetro do problema. Uma vez que sua expressão depende da morfologia e do tamanho da partícula, um tempo característico de rotação de GNPs e MWCNTs difere.

Conteúdo da Figura 8 análogo ao da Figura 6 dependências do ângulo de inclinação dos GNPs em relação à direção do campo aplicado no tempo de ação do campo quando L _R foi avaliada pela Eq. (5). Os resultados foram encontrados para dois valores de intensidade de campo:1 kV / m (Fig. 8а) e 36 kV / m (Fig. 8b) supondo que as partículas estão quase completamente desordenadas no momento inicial ( Θ ( t =0) = π / 2.05). Para efeito de comparação, os resultados dos cálculos da dependência do ângulo para MWCNTs ( L _x foi avaliada pela Eq. (2)) são introduzidos nos mesmos gráficos.

A evolução do ângulo de inclinação das partículas de enchimento de carbono em relação à direção do campo estimada na aproximação de elipsóides para MWCNTs e em aproximação de esferóides para GNPs na intensidade do campo elétrico AC 1 kV / m ( a ) e 36 kV / m ( b )

A Figura 9 mostra as dependências do ângulo de inclinação dos GNPs em relação à direção do campo aplicado no tempo de ação do campo em uma aproximação de que o GNP é um esferóide com fator de despolarização (4). A avaliação foi realizada para a intensidade do campo elétrico AC de 1 kV / m (Fig. 9а) e 36 kV / m (Fig. 9b), supondo que no momento inicial a partícula está aproximadamente desordenada ( Θ ( t =0) = π / 2.05).

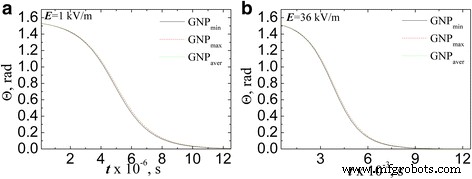
A evolução do ângulo de inclinação do GNPs em relação à direção do campo estimado na aproximação esferóide ( L _x foi levado pela Eq. (4)) na intensidade do campo elétrico AC 1 kV / m ( a ) e 36 kV / m ( b )

A partir da análise apresentada nos dados da Fig. 9, as seguintes conclusões foram feitas:em primeiro lugar, se assumirmos que o eixo do campo elétrico é codirigido com o x -eixo do GNP, o tempo de rotação aumenta significativamente em comparação com o cálculo no caso do eixo do campo e da codirecção do raio do GNP. E esse comportamento independe da proporção do PNB. Em segundo lugar, o curso da dependência é minimamente diferente para as partículas com diferentes proporções de aspecto e, em um determinado ponto do tempo do processo, a partícula mais alinhada é a partícula com proporção de aspecto mínima GNP _min enquanto GNP _aver e GNP _max ângulos coincidem. Esse comportamento se deve ao valor do fator despolarizante próximo a 1 para os casos acima.

Assim, as estimativas mostraram que o tempo de rotação das partículas de carbono sob a ação do campo elétrico AC depende de sua morfologia e razão de aspecto. Observe que o modelo considera uma partícula embutida na matriz polimérica enquanto no compósito, temos um conjunto de partículas com diferentes ângulos iniciais de inclinação. Essa é uma das razões pelas quais o tempo real característico de toda a formação da rede pode ser muito diferente do tempo estimado.

Além disso, é complicado conseguir tal distribuição de MWCNTs na mistura composta onde cada tubo individual está emaranhado. Sabe-se que os nanotubos de carbono tendem a se enredar devido à interação de suas superfícies. Portanto, o tempo real de MWCNTs no alinhamento da mistura composta é significativamente maior do que foi estimado teoricamente. Além disso, a viscosidade da mistura composta com o mesmo conteúdo de MWCNTs é maior do que a viscosidade da mistura composta com GNPs. Todos esses fatores impedem um alinhamento tão rápido de MWCNTs no composto como foi estimado.

Propriedades elétricas de compostos sólidos

No estudo, foram encontrados experimentalmente valores de resistividade dos compósitos GNPs / Larit 285 preparados com distribuição alinhada e com distribuição aleatória de filler em matriz epóxi. A Figura 10 apresenta as dependências da concentração da condutividade elétrica dos compósitos GNPs / Larit 285 com distribuição alinhada e aleatória de preenchimento. As propriedades elétricas das amostras compostas foram investigadas longitudinalmente e perpendicularmente às aplicadas na direção do campo elétrico de fabricação dos compósitos. A Figura 11 apresenta as dependências da concentração da condutividade para compósitos MWCNTs / Larit 285 (а) [27] e GNPs / Larit 285 (b) em escala log-log.

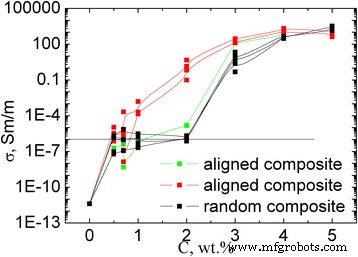
Dependência da concentração da condutividade elétrica de compósitos GNPs / Larit 285 com distribuição de preenchimento alinhado e com distribuição aleatória em escala logarítmica

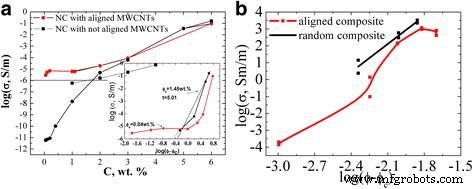
Dependência da concentração da condutividade de MWCNTs / Larit 285 ( а ) [27] e GNPs / Larit 285 ( b ) em escala log-log

Os valores mais baixos da condutividade σ correspondem às amostras de resina epóxi sem enchimento (condutividade de 10 ⁻¹¹ Sm / m). Com a adição de GNPs ao composto, sua condutividade aumenta e atinge o valor de σ =10 ⁻⁶ Sm / m (este valor é considerado como nível de percolação) no conteúdo GNPs с em composto de φ _с =2% em peso para os compósitos com distribuição aleatória de enchimento. Para os compósitos GNPs / Larit 285 com distribuição de enchimento alinhada, a concentração de percolação é de φ _с =0,84% em peso. Thus, materials of the identical composition are characterized by different values of percolation threshold depending on the method of preparation and filler distribution in the polymer matrix (aligned or random).

Conductivity of GNPs/Larit 285 composites smoothly increases with the increment of GNPs content for both types of the samples while the shape of the dependence is completely different for the MWCNTs/Larit 285 composites obtained by the same method [27] (see Fig. 11). Concentration dependence of conductivity of MWCNTs/Larit 285 composites increases with the increment of MWCNTs content at low filler content until it reaches a plateau, then conductivity increases again. Such a difference of conductivity concentration dependence can be explained by another process of conductive network formation if the fillers are of different morphology. MWCNTs/epoxy composites are characterized by crossed framework structure formation while in GNPs/epoxy composites chained structure appears. GNPs addition to the polymer matrix smoothly increases the number of conductive links in composite. In case of entangled by themselves frame MWCNTs, there is an area where nanotubes addition to the matrix has little effect on its conductivity.

Statistical percolation model operates with probabilities of particles in composite to create a conductive chain at their certain content. As it was shown in our paper, manufactured with electric field treatment, composites become conductive at lower content of carbon filler due to activation of dynamic percolation which is a phenomenon when conductive chain formation is stimulated by external influences at such a content of conductive particles in composite which is not enough for statistical percolation.

It should be noted that the existence of two types of percolation transitions is a characteristic feature of composite materials which are in low-viscosity state during the manufacture [34]. The higher value of percolation concentration cannot be changed by varying the manufacturing conditions of the composite since it is defined by statistical percolation theory. Statistical percolation threshold is defined by the filler type, its aspect ratio, surface state of polymer and filler, wettability, uniformity of filler distribution, and its content in polymer matrix. As we have shown, dynamical percolation threshold can be shifted by activating of filler particle movement in polymer matrix, by electric field action, and, thus, promoting a conductive network formation. The value of dynamic percolation threshold can be changed with method of composite manufacture change. We have established that in case of filler alignment under electric field action, dynamical percolation threshold is defined not only by the above parameters but also by parameters of the applied field and polymer matrix viscosity, filler morphology.

Conclusions

1.
Nanocarbon-polymer composite material with aligned distribution of graphite nanoparticles in epoxy matrix has been produced by exposing to a high-voltage AC electric field. The influence of electric field treatment time, strength, and configuration of electric field on formation of aligned GNPs network in liquid polymer medium was investigated by optical microscopy.
2.
It was shown that the influence of AC electric field at composite fabrication process leads to the manifestation of two types of percolation transitions:statistical and dynamic ones. In addition, the aspect ratio of the filler particles and the character of the formation of the conducting cluster, depending on the shape of the particles, determine the shape of the σ =f(c) dependence and the critical concentration of both dynamic and statistical percolation thresholds.
3.
The effects of the morphology of the filler particles on the process of nanocarbon alignment in polymer matrix under AC electric field have been investigated by estimating of carbon nanotube and graphite nanoplatelet rotation time using an analytical model based on effective medium approach. The theoretical evaluation of characteristic time of carbon nanoparticle of different morphology rotation under AC electric field action have shown that rotation time of carbon nanoparticle is determined by its depolarization factor which in turn depends directly on the aspect ratio of particle.
4.
The investigation of concentration dependences of conductivity of composites GNPs/Larit 285 with aligned by AC electric field action filler distribution and random filler distribution in epoxy matrix have shown that under AC electric field action composites, percolation threshold decreases essentially from ϕ _c =2 wt% for composites with random filler distribution of GNPs to ϕ _c =0.84 wt% for the obtained under AC electric field action GNPs/Larit 285 composites.

Abreviações

AC:: Alternative current
AFM:: Força atômica microscópica
CNTs:: Nanotubos de carbono
DC:: Direct current
GNPs:: Graphite nanoplatelets
MWCNTs:: Multiwall carbon nanotubes
SEM:: Microscopia eletrônica de varredura

Investigação teórica de nanofios de germânio deformados biaxialmente por tração Fabricação de alto rendimento de nanofibras de qualidade usando eletrofiação de superfície livre modificada

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias