As propriedades elétricas de compostos híbridos baseados em nanotubos de carbono multifoliados com nanoplacas de grafite

Resumo

No presente trabalho, investigamos as dependências da concentração da condutividade elétrica de compósitos de monopolímero com nanoplacas de grafite ou nanotubos de carbono multipolar e compósitos híbridos com nanotubos de carbono multipolar e nanoplacas de grafite. O último enchimento foi adicionado a determinados sistemas em um teor de 0,24% em volume. O conteúdo de nanotubos de carbono multifoliados é variado de 0,03 a 4% em volume. Antes da incorporação na resina epóxi, as nanoplacas de grafite foram submetidas a tratamento com ozônio ultravioleta por 20 min. Verificou-se que a adição de nanocarbono à suspensão de baixa viscosidade (polímero, acetona, endurecedor) resulta na formação de duas transições de percolação. A transição de percolação dos compósitos à base de nanotubos de carbono é a mais baixa (0,13 vol%).

Foi determinado que a combinação de duas cargas eletrocondutoras no polímero de baixa viscosidade resulta em um efeito sinérgico acima do limite de percolação, que é revelado no aumento da condutividade em até 20 vezes. O cálculo do número de cadeias condutoras no compósito e da resistência elétrica de contato no âmbito do modelo de resistividade elétrica efetiva nos permitiu explicar a natureza do efeito sinérgico. A redução da resistência de contato elétrico em compósitos híbridos pode estar relacionada a uma camada mais fina de polímero entre as partículas de carga e o número crescente de partículas que participam do circuito eletrocondutor.

Histórico

Usar vários enchimentos simultaneamente (principalmente misturas) é a tendência dos últimos anos, pois pode melhorar significativamente as propriedades dos materiais compostos produzidos (CMs), como condutividade elétrica e térmica, propriedades elásticas - resistência, módulo de Young, temperatura de transição vítrea e mecânica perdas em comparação com CM com um único enchimento. A adição de uma carga multicomponente a uma matriz polimérica promove a interação entre essas cargas. Assim, a condutividade melhorada como resultado do efeito sinérgico foi observada em CMs à base de polietileno com partículas de grafite e fibras de carbono (CFs) [1], bem como em CMs contendo negro de fumo e CFs [2, 3]. O mecanismo de aumento da condutividade consiste em dupla percolação e representa a função dos CFs no aumento da conectividade de caminhos condutores. A coexistência de duas redes condutoras formadas por partículas de negro de fumo e fibras de carbono se reforçando, leva a uma melhora significativa nas características elétricas do CM, uma vez que o filler fibroso interage com partículas esféricas de negro de fumo que estimula a formação de rede condutiva em um matriz polimérica.

A percolação clássica com uma transição abrupta de um estado não condutivo para um estado condutor é comumente esperada para compósitos preenchidos com partículas altamente condutoras. Até agora, vários modelos e equações diferentes foram propostos para uma descrição do comportamento da condutividade [4, 5].

No entanto, em muitas observações experimentais, a percolação em compósitos é mais complicada. A presença de transições de percolação de duas etapas (percolação dupla), várias etapas (percolações múltiplas) e até difusas (manchadas) foi relatada [6,7,8,9,10,11,12]. O caráter do limiar de percolação é determinado pela distribuição de partículas, seus tipos e tipos de contatos elétricos, efeitos geométricos e distribuição seletiva de partículas condutoras em meios de múltiplos componentes (por exemplo, em misturas de polímeros). A existência de processos de formação de rede estática e cinética, bem como a estrutura núcleo-casca das partículas, podem ser responsáveis ​​pelos múltiplos limiares de percolação.

O efeito sinérgico pode aparecer na melhoria das propriedades elétricas ou térmicas dos CMs, mesmo quando um dos enchimentos não é altamente eletricamente ou termicamente condutivo. Em [13], Kim et al. investigou CMs com base em poliéter éter cetona (PEEK) com enchimentos híbridos de SiC e CF. Foi observada melhora significativa na condutividade térmica do CM, que é o resultado da formação de caminhos térmicos efetivos no CM.

Existem trabalhos recentes que apresentam os resultados de pesquisas dos compósitos com cargas em nanoescala [14, 15] e suas misturas. Assim, foi mostrado em [16] que a adição de nanotubos de carbono (CNT) no CM com negro de fumo aumenta a condutividade do CM. Além disso, as partículas de negro de fumo também aumentam a viscosidade e a resistência a rachaduras dos nanocompósitos, confirmando assim um efeito sinérgico do negro de fumo como um enchimento multifuncional. Em [17, 18], Zhao et al. investigou compósitos com nanotubos de carbono e nanoplacas de grafite (GNPs). A transição de baixa percolação foi observada devido à melhor interação entre diferentes cargas de carbono como resultado de um processo modificado de fabricação das amostras. Não são adicionadas partículas individuais de cargas de carbono ao polímero e nanoplacas de grafite nas quais os nanotubos de carbono são cultivados e alinhados. Essas estruturas são consideradas como uma partícula híbrida inteira, que possui uma morfologia complexa.

Nós investigamos os materiais compostos de polímero híbrido consistindo de componentes condutores e dielétricos [19, 20]. Os resultados mostraram que o filler dielétrico esfolia nanoplacas de grafite e desembaraça nanotubos de carbono em solução de resina em solvente de acetona durante a fabricação de compósitos. Isso levou a melhores propriedades elétricas e térmicas das amostras.

Compósitos de polímero híbrido são muito tópicos agora. Mas todas as combinações de vários enchimentos e vários polímeros levam a resultados positivos? Claro que não! Em primeiro lugar, poucas pesquisas foram realizadas nesta área; em segundo lugar, simulações teóricas de vários sistemas híbridos e suas propriedades apresentam excelentes resultados, mas nem sempre são confirmados experimentalmente [21].

A novidade deste trabalho é que para obtenção do efeito sinérgico, são utilizados dois fillers condutores com a forma geométrica única e diferentes relações de aspecto, bem como as diferentes características de dispersão.

Métodos

Materiais

A Figura 1a apresenta a imagem SEM de nanotubos de carbono multi-parede usados ​​(MWCNTs) com pureza ≥90% (Cheap Tubes Ins.). A imagem de microscopia óptica de GNPs que foi usada como o segundo preenchimento é mostrada na Fig. 1b.

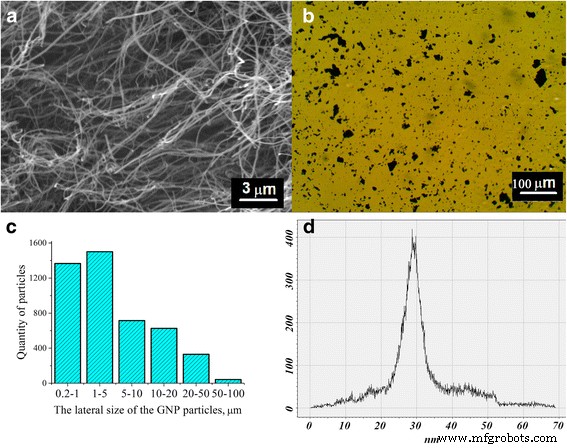
Imagens SEM para o MWCNT ( a ) Imagem ótica para o PNB ( b ) As distribuições de partículas (diagrama) no tamanho lateral do TEG após 30 h de dispersão ultrassônica em água (GNPs) ( c ) Histogramas de distribuição de espessura de GNPs obtidos em meios dispersivos - em água ( d )

Grafite expandida termicamente (TEG) é um produto de grafite dispersa natural ( d =50–300 μm, h =5–30 μm) intercalação com H ₂ SO ₄ e posterior tratamento térmico em um forno com fluxo ascendente de acordo com o método desenvolvido e relatado em artigo publicado anteriormente [22]. A peculiaridade do processo de ultra-som TEG no meio aquoso é que as partículas de TEG não afundam, mas flutuam na superfície. Por esta razão, a esfoliação TEG em GNPs é complicada. Após 30 h de ultrassom TEG em meio aquoso, a maior parte dos PNBs tem 0,2–5 µm de diâmetro; no entanto, grandes partículas de 10–100 µm de diâmetro também ocorrem (Fig. 1c).

Com base em imagens AFM convertidas em 3D de GNPs obtidas em diferentes meios dispersivos, realizamos uma análise comparativa das espessuras de GNP. Os histogramas de distribuição de espessura são apresentados na Fig. 1d. Com base nos resultados do AFM, a variação da distribuição da espessura para GNPs (obtida em meio de água) foi de 5–55 nm com o máximo de distribuição a 28 nm. A estimativa das dimensões laterais permitiu o cálculo da razão de aspecto dos PNBs que é de ~ 40–900 para os PNB. Portanto, pode-se concluir que os PNB obtidos em meio dispersivo em água possuem ampla distribuição de espessuras e dimensões laterais. Isso é certamente favorável para maior condutividade elétrica do composto com o enchimento deste tipo.

As características estruturais e morfológicas das cargas investigadas são apresentadas na Tabela 1. Como pode ser visto na Tabela 1 e na Fig. 1, a forma de uma carga de nanocarbono difere consideravelmente. Assim, GNPs podem ser considerados como discos e MWCNTs como cilindros.

Preparação de Compósitos

Este artigo apresenta os resultados da investigação das mudanças de resistividade elétrica e condutividade térmica de compósitos poliméricos híbridos com nanotubos de carbono de parede múltipla (MWCNTs) mediante a adição de uma quantidade constante do segundo enchimento em forma de disco eletricamente condutor - nanoplacas de grafite.

Para o estudo das propriedades elétricas de compósitos poliméricos de carbono-resina epóxi, dois sistemas foram preparados:

• 
  ➢ Sistema de dois componentes, onde GNPs ou MWCNTs de paredes múltiplas foram usados ​​como enchimentos— materiais mono compostos (MCMs)
  
• 
  ➢ Sistema de três componentes, onde GNPs de enchimento eletricamente condutivo foi usado como o segundo enchimento para CMs com MWCNTs— materiais compostos híbridos (HCMs)
  

Materiais mono compostos

Durante nosso trabalho, sintetizamos e investigamos os sistemas compostos à base de epóxi Larit 285 (Lange Ritter GmbH, Alemanha). Esta resina tem as seguintes características:equivalente de epóxi =165-170, número de epóxi — 0,59 ÷ 0,65.

A fim de preparar MCMs de nanocarbono / epóxi, os preenchimentos de nanocarbono foram incorporados à resina epóxi Larit 285 (viscosidade de 600-900 mPa s) com H285 (viscosidade - 50 ÷ 100 mPa s, número de amina - 480 ÷ 550 mg KOH / g) como um agente de endurecimento. O conteúdo da carga de nanocarbono em MCMs variou de 0,03 a 4% em volume.

O pó de GNP foi submetido a tratamento UV / ozônio (para CMs mono e híbridos). O tratamento UV / ozônio foi realizado com a utilização da lâmpada DRT-1000. Os pós GNP iniciais foram submetidos a tratamento com UV / ozônio por 20 min [22, 23].

Três gramas do epóxi Larit 285 foram colocados no tubo de ensaio para posterior dissolução no solvente de acetona. O nanocarbono em pó foi pesado para a concentração selecionada e adicionado à solução de epóxi-acetona. A carga de nanocarbono (GNPs ou MWCNTs) foi mecanicamente misturada com resina epóxi e acetona. Uma mistura desses componentes foi agitada durante 30 min (para GNPs) ou 60 min (para MWCNT) em um banho ultrassônico para uma distribuição mais uniforme do enchimento no polímero, então o agente de cura H285 foi adicionado e uma mistura foi vertida em moldes e curados em temperatura ambiente por 48–72 h para completar a polimerização.

Materiais compostos híbridos

MWCNTs foram usados ​​para a preparação de HCMs, como um enchimento eletrocondutor principal com concentrações variando de 0,03 a 4 vol%. Para estudar as propriedades sinérgicas do enchimento elétrico disperso adicional, GNPs foram adicionados aos sistemas dados em um teor de 0,24 vol%.

MWCNTs foram misturados com resina epóxi e acetona. Uma mistura desses componentes foi agitada durante 60 min em banho ultrassônico para uma distribuição mais uniforme do filler no polímero. Em seguida, o pó de GNP foi adicionado e completamente misturado mecanicamente, e todos foram agitados durante 30 min em banho ultrassônico. Em seguida, o agente de cura H285 foi adicionado e uma mistura foi derramada em moldes e curada em temperatura ambiente por 48-72 h para completar a polimerização.

Para as medidas de condutividade elétrica, as amostras com formato de paralelepípedo retangular com tamanho de 3,5 × 3,5 × 10 mm ³ estavam preparados. A faixa de condutividade de medição foi de 10 ⁻¹² a 10 S / m.

Métodos de teste

A dispersão ultrassônica do pó de TEG foi realizada em banho ultrassônico “BAKU” BK-9050, frequência US - 40 kHz, com potência elétrica máxima de 30 e 50 W. As dimensões laterais dos GNPs preparados foram investigadas usando um microscópio óptico MIKMED-1 com a câmera digital ETREK DCM-510 e sonda NanoLaboratory INTEGRA. Para estimar a espessura e o diâmetro médios dos GNPs, suas imagens de microscópio óptico e de força atômica (AFM) foram convertidas em imagens 3D pelo programa Nova, que criou os histogramas de distribuição da densidade do GNP.

O tratamento de UV / ozônio foi realizado utilizando DRT-1000 (lâmpada ultravioleta) equipada com lâmpada de arco de descarga elétrica de alta pressão inflada com composto de mercúrio e argônio que poderia liberar radiação ultravioleta de 50 W no comprimento de onda de 240–320 nm. A distância entre a lâmpada ultravioleta e a amostra foi fixada em 11 cm.

A resistência elétrica das amostras foi medida por duas sondas ( R =10 ⁴ –10 ⁹ Ω) e quatro sondas ( R ≤ 10 ⁴ Ω) método ou por teraohmímetro E6-13 ( R =10 ⁹ –10 ¹³ Ω). Uma instalação automatizada foi usada para a investigação da resistência elétrica na faixa de temperatura de 6–300 K. Os principais componentes da instalação automatizada foram uma haste para uma amostra, uma direção de corrente de comutação de energia e uma fonte estável de tensão, um analógico –Conversor digital ADC 16-32F (SDI), um computador pessoal e os cabos de interface. A temperatura foi medida por um termopar de cobre-constantan localizado próximo à amostra. A faixa de medição da resistência elétrica (0,01–10 ¹⁴ Ω) foi dividido em várias regiões:0,01–2,5 Ω, onde o erro não excede 0,5%; 2,5–10 ⁷ Ω (o erro foi <1%); R =10 ⁸ Ω (<5%); R =10 ⁹ Ω (<10%); R =10 ¹⁰ –10 ¹³ Ω (<20%). Ao medir a resistência elétrica dos CMs, três amostras para cada concentração foram testadas.

Resultados e discussão

Condutividade elétrica dos compostos de polímero com enchimentos mono e híbridos

O limite de percolação ϕ _cr foi investigado usando medições de condutividade de volume. A dependência da condutividade elétrica volumétrica dos compósitos preparados com o teor de carga é mostrada na Fig. 2. Os valores para as concentrações mais baixas correspondem à condutividade da resina epóxi pura de 7,9 × 10 ⁻¹² ° S / m.

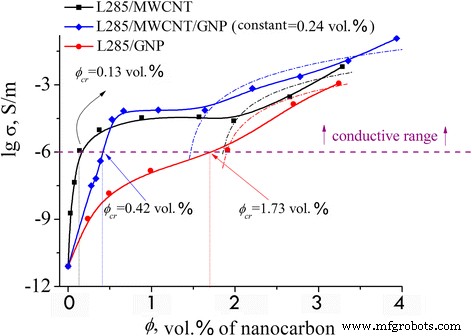
Condutividade elétrica de compósitos em função do teor de nanocarbono. Linha sólida as curvas experimentais; linha pontilhada as curvas calculadas de acordo com a Eq. (1)

Como pode ser visto na Fig. 2, as dependências da condutividade da concentração para ambos os MCMs e HCMs têm duas transições de percolação. O mais baixo (em 0,13 vol%.) Foi encontrado para amostras com MWCNTs. Começando em 0,137 vol% de MWCNTs, os valores de condutividade são maiores que 10 ⁻⁶ S / m representando a faixa condutiva. Para amostras baseadas em PNB, a concentração crítica mais alta ϕ _cr igual a 1,7% em volume é observado, e há apenas uma transição de percolação acima do valor de condutividade de 10 ⁻⁶ S / m. Para amostras com os enchimentos mistos com concentração constante de GNPs ( ϕ =0,24 vol%.), A concentração crítica de MWCNT / GNP foi considerada igual ϕ _cr =0,42 vol% e situado entre os valores dos compósitos com fillers puros.

Comportamento semelhante de σ ( ϕ ), a saber, a presença de duas transições de percolação na curva de concentração foi observada para uma série de compósitos [24,25,26,27].

Josef Z. Kovacs e outros [24] consideram que tais limiares de percolação induzidos por processos cinéticos e, portanto, não podem ser determinados usando a lei de escalonamento de percolação comum da teoria estatística de percolação.

Além disso, a transição de dupla percolação foi obtida por Mamunya e outros em [25]. Os autores também usaram os compósitos polímero-nanotubos de carbono, mas combinaram dois polímeros (copoliamida e polipropileno) como uma matriz polimérica, que misturaram com o filler em altas temperaturas (125, 167 ° C) e prensaram a 180 ° C.

Supomos que a existência de dois limiares de percolação em nosso trabalho é uma característica dos materiais compósitos que apresentam baixa viscosidade na fase de fabricação da amostra (Fig. 2 e Tabela 2).

Acreditamos que a primeira transição de percolação pode ser considerada como uma transição de percolação quase dinâmica por analogia com a transição de percolação dinâmica observada em compósitos polímero-carbono, onde a transição de percolação é formada sob a ação de forças externas (campo elétrico ou magnético, pressão , etc.) [24, 27].

Na região de baixa concentração, após a adição do endurecedor, o polímero líquido com nanocarbono apresenta baixa viscosidade. As partículas do enchimento de carbono na matriz polimérica podem ser representadas como aglomerados suficientemente grandes de nanopartículas (mesmo apesar da dispersão ultrassônica de longa duração) e nanopartículas separadas (nanotubos ou GNPs) com mobilidade suficientemente alta em uma matriz polimérica de baixa viscosidade. Sob a ação de van der Waals ou forças eletrostáticas, essas nanopartículas separadas (nanotubos) podem se mover conectando-se entre si, bem como com grandes aglomerados de nanopartículas. Assim, devido a esse deslocamento, até que a matriz polimérica endureça, essas nanopartículas móveis separadamente podem formar cadeias condutoras que fornecem a condutividade de toda a amostra.

A formação da "plataforma" ou platô após o limiar de percolação quase dinâmica na dependência da concentração da condutividade elétrica para CMs com MWCNTs e enchimento híbrido (onde a concentração de CNT domina) depende de vários fatores. Está principalmente relacionado ao aumento da concentração de enchimento, o que leva a um aumento da viscosidade da amostra não curada e movimento restrito das partículas separadas para formar novas cadeias condutoras. Secundariamente, o número de partículas móveis separadas também aumenta. Além disso, o aumento simultâneo da viscosidade e do número de nanopartículas individuais capazes de movimentar com eficiência desacelera o processo de formação das cadeias condutoras e, conseqüentemente, o crescimento da condutividade com o aumento da concentração de filler. É visto na Fig. 2 que, para atingir a segunda concentração crítica, é necessário adicionar uma quantidade significativa de enchimento ao CM. Então, partículas únicas começam a interação umas com as outras, bem como aglomerados de partículas e aglomerados de partículas com um único CNT.

A transição de percolação quase dinâmica não pode ser descrita na estrutura da teoria de percolação clássica (Fig. 3a). A segunda transição de percolação é definida e descrita pela teoria estatística de percolação (Fig. 3b-d) [28, 29]:

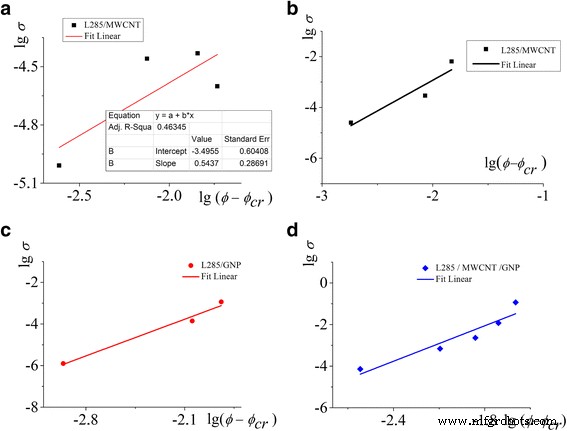
a - d Dependência de escala (lg σ como uma função de lg (ϕ - ϕ _cr )) para determinar os parâmetros da Eq. (1). a A transição de percolação quase dinâmica, b , c , d A teoria estatística da percolação
$$ \ sigma \ left (\ phi \ right) \ sim B {\ left (\ phi - {\ phi} _ {\ mathrm {cr}} \ right)} ^ t $$ (1)
onde ϕ _cr é a concentração crítica (limiar de percolação), t é o índice crítico e B é a constante de proporcionalidade no modelo clássico de percolação. As constantes B , ϕ _cr , e t foram ajustados usando o método de minimização do erro quadrático médio (Fig. 3, Tabela 2). Os valores ajustados de ϕ _cr estão incluídos na Fig. 2.

Na Fig. 4, apresentamos a condutividade elétrica versus a concentração para MCM – L285 / MWCNT e HCM – L285 / MWCNT / GNP. Como se pode ver na foto, a transição de percolação é a mesma para os dois compósitos. Um efeito sinérgico é observado como aumento da condutividade elétrica de HCM acima da concentração crítica (Fig. 4). O maior efeito sinérgico foi observado em CM com a combinação de dois enchimentos eletricamente condutores - nanotubos de carbono e nanoplacas de grafite - e na concentração de 2 vol%, a condutividade elétrica é 20 vezes maior e a 4 vol%, 10 vezes maior em comparação com MCM .

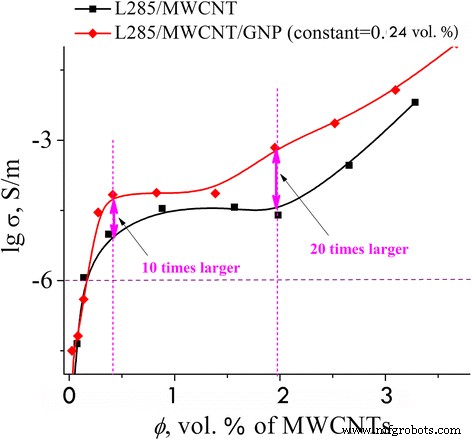
Condutividade elétrica de compósitos em função do conteúdo de MWCNTs

Para entender o mecanismo de formação de cadeias condutoras no híbrido CM onde o efeito sinérgico é observado, ilustramos o possível esquema na Fig. 5. Para desembaraçar os feixes de CNTs, eles são submetidos à dispersão ultrassônica. Como resultado, nem todos os CNTs são desvendados, além de se fragmentarem reduzindo sua relação de aspecto; assim, o número de CNTs necessários para a formação das cadeias condutoras aumenta.

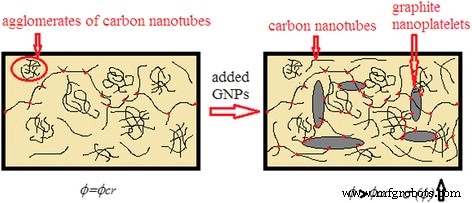
Princípios de formação da via condutiva no híbrido CM – L285 / MWCNT / GNP

A fim de obter um efeito sinérgico, concebemos adicionar uma pequena quantidade de partículas de GNP em um composto com CNT para a conexão de aglomerados não totalmente desvendados de CNTs. Devido ao meio líquido (ou seja, uma resina de baixa viscosidade) e uma percolação quase dinâmica, não conseguimos atingir um limiar de percolação inferior ao de mono CM com CNTs. Podemos explicá-lo apenas pelo fato de que no caso de transição de percolação ultrabaixa (0,13 vol%), as cadeias condutivas contínuas não são formadas em grande número (é visto na Fig. 4, uma vez que os valores de condutividade são baixos em a primeira transição de percolação) principalmente de partículas separadas de CNT, que não são agrupadas e ainda não têm contato com as partículas de GNP. Após o limiar de percolação, um aumento significativo da condutividade do híbrido CM é observado devido às cadeias adicionais de aglomerados de CNTs e GNPs (Fig. 5).

As características morfológicas do componente condutor de nanocarbono do enchimento são criticamente importantes durante a formação de cadeias condutoras. A quantidade total de cadeias (portanto, a resistência de contato entre as partículas e as características de percolação) no CM é afetada principalmente pela forma do enchimento (forma de esqueleto de CNT e forma semelhante a uma cadeia de GNP). Para investigar o número de cadeias e a resistência de contato entre as partículas no CM, utilizamos um modelo de resistência elétrica efetiva.

Nos termos do modelo proposto, a resistência elétrica da cadeia consistia em partículas de nanocarbono que são as seguintes [30]:
$$ {R} _ {\ mathrm {CM} \ _ \ mathrm {G} \ mathrm {N} \ mathrm {P} \ left (\ mathrm {MWCNT} \ right)} =\ frac {N _ {\ mathrm { GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {em} \ _ \ mathrm {cadeia}}} {N _ {\ mathrm {cadeia} \ _ \ mathrm {em} \ _ \ mathrm {C } \ mathrm {M}} ^ {*}} \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) $$ ( 2)
onde \ ({N} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {in} \ _ \ mathrm {cadeia}} =\ frac {b \ left (1 \ kern0 .5em \ mathrm {cm} \ right) \ cdot \ gamma} {l} =\ frac {\ gamma} {l} \) é a quantidade de partículas de nanocarbono em uma cadeia, b é o comprimento da amostra (1 cm), γ é o fator constante com valor de 1 a 2, l é o comprimento da partícula de nanocarbono (GNP ou CNT), r _{GNP (MWCNT)} é a resistência elétrica da partícula de enchimento (para as partículas semelhantes a disco - \ ({r} _ {GNP (disco)} ={\ rho} _ {GNP} \ cdot \ frac {d} {d \ cdot h} =\ frac {\ rho_ {GNP}} {\ mathrm {h}} \), para o cilíndrico - \ ({r} _ {\ mathrm {MWCNT} \ left (\ mathrm {cilindro} \ right)} ={\ rho} _ {\ mathrm {MWCNT}} \ cdot \ frac {4 l} {\ pi {d} ^ 2} \)), h é a espessura da partícula de nanocarbono, d é o diâmetro, e R _к é a resistência elétrica do contato único entre as partículas da carga (CNT ou GNP).

Resumindo, a resistência elétrica do CM de polímero / nanocarbono pode ser avaliada como [30]:
$$ {R} _ {\ mathrm {CM} \ _ \ mathrm {G} \ mathrm {N} \ mathrm {P} \ left (\ mathrm {MWCNT} \ right)} =\ frac {N _ {\ mathrm { GNP} \ left (\ mathrm {MWCNT} \ right) \ _ \ mathrm {em} \ _ \ mathrm {cadeia}}} {N _ {\ mathrm {cadeia} \ _ \ mathrm {em} \ _ \ mathrm {C } \ mathrm {M}} ^ {*}} \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) =\ frac {\ gamma ^ 2 \ pi \ cdot z} {4 F} {\ left (\ frac {F - {\ phi} _ {\ mathrm {cr}}} {\ phi - {\ phi} _ {\ mathrm { cr}}} \ right)} ^ t \ cdot \ left ({r} _ {\ mathrm {GNP} \ left (\ mathrm {MWCNT} \ right)} + {R} _K \ right) $$ (3)
onde N ^* _{chain_in_CM} é o número de cadeias de nanocarbono conectadas em paralelo. Esse número é proporcional à quantidade total de partículas, participando da eletrocondução. F é o fator de embalagem ( F =0,05 para GNP e F =0,06 para CNT), z = h é para GNP e \ (z =\ frac {d ^ 2} {l} \) é para CNT. Este modelo leva em consideração não apenas a concentração crítica ϕ _cr , fator de embalagem F , e resistividade elétrica do enchimento r _{GNP (MWCNT)} mas também a morfologia das partículas (razão de aspecto).

Em termos do modelo proposto, foram calculados os valores seguidos:dependência da concentração da condutividade elétrica σ _dc ( ϕ ), contate a resistência elétrica R _к , e número de cadeias ininterruptas N ^* _{chain_in_CM} (ver Fig. 6, Tabela 3).

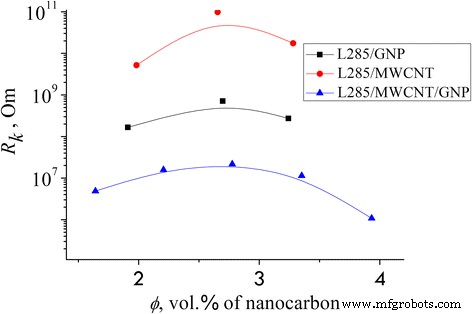
Resistência de contato R _k dos MCs estudados, que foi calculado usando a Eq. (3)

Como podemos ver na Tabela 3, o valor da resistência elétrica de contato R _к exibe no mínimo 10 ⁺⁶ –10 ⁺⁷ Ω para preenchimento híbrido e máximo próximo a 10 ⁺⁹ –10 ⁺¹⁰ Ω para o CM com base no CNT. Os CMs baseados em CNT têm 300 (600) vezes maior quantidade total de cadeias ininterruptas N ^* _{chain_in_CM} do que os CMs com base no GNP (filler híbrido) com concentração de 2,70 vol%. A condutividade elétrica de L285 / MWCNT / GNP é maior do que a condutividade elétrica de um CM binário (Fig. 2).

Por outro lado, a formação da rede condutora de partículas de nanocarbono não causaria necessariamente alta condutividade elétrica. Segundo [31], simulações numéricas mostraram que a resistência de contato entre diferentes nanotubos varia de 100 kOhm a 3,4 MOhm e depende fortemente da estrutura atômica da superfície de contato e do relaxamento estrutural das partículas. A resistência de contato pode aparecer durante a formação da camada dielétrica entre os pontos de contato dos componentes de enchimento (devido ao umedecimento). Esta camada dielétrica causa degradação da condutividade e estimula o tunelamento dos portadores de carga [32].

Resistência elétrica R _к entre duas partículas em contato pode ser avaliada da seguinte forma [33]:
$$ {R} _ {k \ left (\ mathrm {tunel} \ right)} =\ frac {V} {w \ cdot j} =\ frac {h ^ 2 \ delta} {w {e} ^ 2 \ sqrt {2 m \ lambda}} \ exp \ left (\ frac {4 \ pi \ delta} {h} \ sqrt {2 m \ lambda} \ right) $$ (4)
onde δ é a espessura da camada de polímero; j é a densidade da corrente do túnel; V é a diferença de potencial; e e m são a carga e a massa de um elétron, respectivamente; h é a constante de Planck; λ é a altura da barreira [34,35,36] (no caso do epóxi λ ≈ 1 eV [33]); e w é o valor de tunelamento transversal.

A Figura 7 mostra que os valores da resistência de contato elétrico no caso do mecanismo de tunelamento da condutividade dependem da distância (espessura da camada de polímero) entre as partículas de enchimento para uma variedade de valores de tunelamento transversal (calculado usando a expressão 4) .

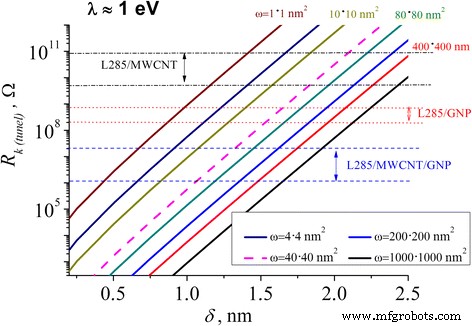
As dependências da resistência de contato na espessura da camada de polímero entre as partículas de enchimento para vários valores do tunelamento em seção transversal w

A Figura 7 demonstra a forte dependência do R _{k (túnel)} em δ . Assim, com o aumento de δ valores de 0,5 a 2,5 nm, R _{k (túnel)} o valor cresceu nove ordens de magnitude, independentemente da seção transversal do túnel w .

Simulações numéricas mostraram que a distância entre as partículas do GNP se degrada lentamente de 1,63 a 1,53 nm para o w =40 × 40 nm ² , que testemunha sobre a ausência de tunelamento e destruição da corrente condutiva para δ ≤ 1,63 nm.

No caso de CMs baseados em CNT, diminuição do δ de 1,83 a 1,57 nm com w =10 × 10 nm ² é causado pelos tamanhos menores do CNT em comparação com os tamanhos do PNB. Assumimos que δ de CM baseado em GNP é menor devido ao tratamento ultravioleta (limpeza da superfície dos grupos funcionais das partículas) e melhor contato entre o polímero e as partículas de carga [22, 23].

CMs com um enchimento híbrido demonstram diminuição de δ de 1,07 a 0,82 nm (de 1,32 a 1,05 nm) para w =10 × 10 nm ² ( w =40 × 40 nm ² )

Como podemos ver na Fig. 7 e na Tabela 3, a espessura da camada de polímero δ para CMs com um enchimento híbrido é o menor, independentemente da magnitude da seção transversal de tunelamento, apesar da maior quantidade de cadeias condutoras em CMs baseados em CNT.

Conclusions

It has been found that two percolation thresholds are formed in polymer solution with nanocarbon with low viscosity. The first is a quasi-dynamic percolation transition which nature is associated with the movement of light separate nanocarbon particles until the mixture is cured. The second percolation transition is static, described by the classical theory of percolation and allowed us to calculate the number of conductive chains and the contact resistance between the filler particles in terms of the model of effective electrical resistivity. It has been found that there is a synergistic effect above the percolation threshold for CMs with a hybrid filler (namely, with the carbon nanotubes and graphite nanoplatelets). It has been shown that a synergistic effect for the CMs with a hybrid filler is possible due to reducing contact resistance between the particles of both fillers, which may be associated with a decrease of the polymer layer thickness between the particles and appearance of moderate amount of the conductive chains with increase of the number of particles involved in a single chain.

Modelo de retenção de TaO / HfO x e TaO / AlO x RRAM com características de chave auto-retificadora Promoção na detecção de acetona de nanobelt SnO2 único pela Eu Doping