Investigação teórica de nanofios de germânio deformados biaxialmente por tração

Resumo

Teoricamente, investigamos nanofios de Ge altamente tensionados lateralmente em GaSb. O método dos elementos finitos foi usado para simular a deformação elástica residual no nanofio de Ge. O incremento de energia total, incluindo energia de deformação, energia de superfície e energia de borda antes e depois da deposição de Ge é calculado em diferentes situações. O resultado indica que o nanofio Ge em GaSb tende a crescer ao longo de 〈100〉 em vez de 〈110〉 nas duas situações e prefere ser exposto por {105} facetas quando depositado uma pequena quantidade de Ge, mas ser exposto por {110 } quando a quantidade de Ge excede um valor crítico. Além disso, os mínimos da banda de condução em Γ -valley em qualquer posição em ambas as situações exibe valores mais baixos do que aqueles em L-valley, levando a uma transição direta de bandgap no nanofio Ge. Para a banda de valência, o máximo da banda do buraco leve em Γ - o ponto é mais alto do que os máximos da banda do orifício pesado em qualquer posição e ainda mais alto do que os mínimos da banda de condução para a deformação hidrostática mais do que ∼5,0%, levando a um bandgap negativo. Além disso, a mobilidade do elétron e do buraco pode ser aumentada devido à diminuição da massa efetiva sob alta tensão de tração. Os resultados sugerem que os nanofios de Ge deformados por tração biaxial possuem propriedades promissoras em aplicações de dispositivos.

Histórico

Como elemento do grupo IV, o germânio (Ge) detém a superioridade tanto em optoeletrônica quanto em eletrônica e tem grande compatibilidade com fotônica de silício (Si). Uma característica essencial do Ge é que seu bandgap direto é de cerca de 0,8 eV (1,55 μ m) a 300 K. A mobilidade do elétron e do buraco no Ge é muito maior do que no Si. Assim, Ge tem sido utilizado em dispositivos de alta velocidade no atual circuito integrado baseado em Si [1, 2]. O mais interessante é que o Ge tensionado por tração oferece otimização nos aspectos acima. Ge é um semicondutor bandgap indireto com uma ligeira diferença de 136 meV entre o vale L e Γ -valley [3]. É teoricamente previsto que mais de ∼4,0% uniaxial ao longo de 〈111〉 [4] ou ∼1,6-2,0% biaxial [5, 6] de deformação de tração pode diminuir a Γ -valley abaixo do vale L, convertendo assim Ge em um material bandgap direto, que abre uma nova rota para a emissão de luz de materiais do grupo IV. Outro ponto importante é que o Ge deformado por tração fornece um aprimoramento significativo na mobilidade da portadora [7, 8] para a realização de dispositivos semicondutores de óxido de metal complementar de alta velocidade.

Nanofios (NWs) exibem propriedades eletrônicas e ópticas atraentes devido à grande relação superfície / volume e confinamento de ambos os portadores e fótons em duas dimensões (2D) [9]. Nos últimos anos, Ge NWs (GeNWs) em Si [10] ou Ge / Si core / shell NWs [11] têm estado sob extenso estudo devido aos seus potenciais em transistores de efeito de campo semicondutores de óxido metálico (MOSFETs) para microeletrônica de Si. Tanto a transcondutância escalonada quanto a corrente foram aumentadas de três a quatro vezes em comparação com o Si convencional p -MOSFET [12]. Assim, espera-se que o crescimento epitaxial de GeNWs laterais diretamente no Si produza MOSFETs de alto desempenho. Zhang et al. abordou que GeNWs ultrafinos em Si (001) são expostos com facetas de {105} [13], que têm a menor energia de superfície prevista [14]. Além disso, o Ge MOSFET deformado em substrato virtual SiGe foi mostrado para melhorar a mobilidade do buraco [1]. Embora GeNW lateral em Si com deformação compressiva possa exibir uma melhora significativa no transporte de portadores, como assumido, eles não podem ser convertidos em um bandgap direto. Para a introdução de deformações de tração em GeNWs, a liga GeSn [15] e os compostos III-Sb [16], que têm uma constante de rede maior do que a do Ge, são necessários. Apesar desse método mecânico ter sido aplicado para a fabricação de GeNWs deformados uniaxialmente [17, 18], o complexo dessa técnica de fabricação dificilmente pode ser adequado para integração monolítica em fotônica e eletrônica baseada em Si. Além disso, a deformação será liberada facilmente em NWs independentes, enquanto GeNWs laterais podem acomodar grande deformação em si mesmos. Assim, GeNWs laterais crescidos epitaxialmente com alta tensão biaxial de tração são necessários para alcançar a transição de bandgap direta, bem como o aumento da mobilidade do portador.

Até o momento, pontos quânticos de Ge livres de deslocamento e altamente biaxiais sob tensão de tração em InP (001) têm mostrado potenciais para emissão direta de bandgap simulada pelo método de elementos finitos (FEM) [19]. Semelhante a isso, neste trabalho, nós teoricamente predizemos a morfologia das superfícies expostas e direção de crescimento de GeNWs biaxialmente tensionados em um modelo de GaSb relaxado que pode ser cultivado diretamente em Si com uma camada tampão de AlSb [16, 20]. Escolhemos {110}, {105} e {111} como superfícies expostas de GeNWs laterais e comparamos a mudança total de energia no sistema de estado estacionário. Ignoramos a influência do deslocamento e da fratura [21] neste sistema altamente tenso para simplificar. A simulação baseada em FEM revela que existe uma quantidade crítica de Ge. Abaixo do valor crítico, GeNWs são expostos por {105}, enquanto acima do valor crítico, eles são expostos por {110}. Quase toda a região GeNW pode ser convertida em bandgap direto, que é a diferença entre os mínimos da banda de condução e os máximos da banda do orifício de luz no Γ -ponto. Além disso, também analisamos qualitativamente a mudança da massa efetiva do portador dependente da deformação no Γ -ponto para prever indiretamente o aumento na mobilidade do elétron e do buraco.

Métodos

Lateral NWs normalmente revelam uma forma de triângulo de seção transversal [22, 23]. Graças à propriedade 1D de NW mostrada na Fig. 1a, um modelo NW finito semelhante a Zhang et al. no material suplementar da Ref. [13] pode ser usado adequadamente para simulação em que as superfícies inicial e final são fixas, mostradas na Fig. 1b. Por causa do efeito de contorno, discutimos apenas a parte central do NW e consideramos que a seção transversal dessa parte representa a situação em um NW infinitamente longo. O FEM é usado para simular a distribuição da deformação de tração em GeNW com incompatibilidade de rede de 7,7% para GaSb. Calculamos o incremento total de energia do sistema após depositar a mesma quantidade de Ge em estado estacionário em três situações:(i) [100] direção de crescimento com {110} facetas expostas (situação A), (ii) [100] direção de crescimento, mas com {105} facetas expostas (situação B), e (iii) [110] direção de crescimento com {111} facetas expostas (situação C). As seções transversais dessas três situações são mostradas na Fig. 1c. As áreas da seção transversal são mantidas as mesmas, representando quantidades iguais de Ge.

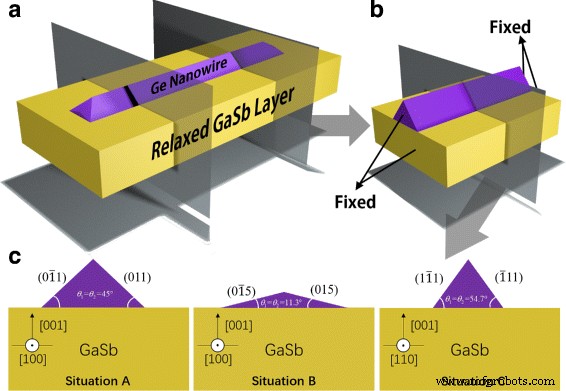
Esquemas de GeNW em GaSb: a Modelo 3D, b modelo finito simplificado e c seções transversais de GeNW com diferentes facetas

A mudança total de energia do sistema por unidade de comprimento (J / nm) inclui a diferença geral na energia de deformação, energia de superfície e energia de borda [24] e pode ser dada por:
$$ \ Delta {{E} _ {\ text {total}}} =\ Delta {{E} _ {\ text {estirpe}}} + \ Delta {{E} _ {\ text {surface}}} + \ Delta {{E} _ {\ text {edge}}}. $$ (1)
O primeiro termo Δ E _{s t r a eu n} representa a diferença de energia de deformação do sistema estável antes e depois da deposição de Ge e é expressa em volume unitário,
$$ \ Delta {u} =\ frac {1} {2 {Y}} \ sum \ limits_ {i =j} ^ {{}} {\ tau_ {ij} ^ {2}} - \ frac {\ nu } {Y} \ sum \ limits_ {i onde τ _ij = C _ij ε _ij ( i, j =1, 2, 3) denotam o tensor de tensão, C _ij e ε _ij são as constantes elásticas e tensor de deformação, respectivamente, Y e G são o módulo de Young equivalente e o módulo de cisalhamento equivalente, respectivamente, e ν é o coeficiente de Poisson equivalente. Na seção transversal 2D considerada, a mudança de energia de deformação total pode ser obtida integrando a área com o valor de Δ u em cada ponto. O segundo termo Δ E _{s u r f a c e} está relacionado à diferença de energia superficial antes e depois da deposição de Ge. A energia de superfície na seção transversal de nossas situações pode ser reescrita como [23]
$$ {{\ gamma} _ {i}} =\ frac {2h} {\ sin {{\ theta} _ {i}}} ({{\ sigma} _ {i}} - {{\ sigma} _ {{(001)}}} \ cos {{\ theta} _ {i}}) $$ (3)
onde h é a altura da seção transversal GeNW, σ _i ( eu =A, B e C) é a energia superficial média das facetas expostas sob a área da unidade, e o anjo correspondente entre as facetas NW e a interface é rotulado por θ _i como mostrado esquematicamente na Fig. 1c. A tensão na energia de superfície pode ser desprezada devido ao seu leve impacto, pois o tratamento na Ref. [25]. A Tabela 1 mostra os valores de energia de superfície da literatura. O último termo chamado mudança de energia de borda significa a mudança de custo de energia para formar bordas afiadas e é dado por
$$ \ Delta {{E} _ {\ text {edge}}} =3 \ varGamma $$ (4)
onde 3Γ é a energia total da borda contendo as interseções das facetas superior e basal. O valor estimado de 3Γ é 3,7 eV / nm pelo ajuste experimental [26] e a influência da energia da borda pode ser ignorada devido ao valor dificilmente variado [25]. Portanto, é válido calcular o incremento de energia de Δ E _total −3Γ.

Depois de conhecer a distribuição da deformação, a banda de condução dependente da deformação diminui no Γ - e o vale L pode ser calculado negligenciando o efeito quântico. A banda de condução do Γ -valley é reduzido apenas com a deformação hidrostática por
$$ \ Delta E_ {c} ^ {\ Gamma} ={{a} _ {c}} ({{varejpsilon} _ {xx}} + {{\ varejpsilon} _ {yy}} + {{\ varejpsilon } _ {zz}}) $$ (5)
onde a _c denota potencial de deformação hidrostática com o valor de -8,24 eV no Γ -ponto [27], ε _xx , ε _yy e ε _zz são a tensão em x , y, e z direção no sistema de coordenadas do material, respectivamente. No entanto, o deslocamento da banda de condução no ponto L está sujeito à deformação hidrostática e de cisalhamento [19], dada por
$$ {{} \ begin {alinhados} \ Delta {E_ {c} ^ {\ mathrm {L}}} =&\ left ({{\ Xi} _ {d}} + \ frac {1} {3} {{\ Xi} _ {u}} \ right) ({{\ varepsilon} _ {xx}} + {{\ varejpsilon} _ {yy}} + {{\ varejpsilon} _ {zz}}) \\ &- \ frac {2} {3} {{\ Xi} _ {u}} \ left (| {{\ varejpsilon} _ {xy}} | + | {{\ varepsilon} _ {yz}} | + | { {\ varejpsilon} _ {xz}} | \ right) \ end {alinhado}} $$ (6)
onde Ξ _d e Ξ _u são o potencial de deformação de dilatação com o valor de -6,97 eV e o potencial de deformação uniaxial com o valor de 16,3 eV no vale L, respectivamente. Para converter Ge em um material bandgap direto, o Γ -valley tem que ser menor que o vale L, o que significa \ (\ Delta {E_ {c} ^ {\ Gamma, \ text {L}}} =\ Delta E_ {c} ^ {\ Gamma} - \ Delta {E_ {c} ^ {\ mathrm {L}}} <- 0,136 \) eV. Aqui, usamos \ (\ Delta {E _ {\ text {DT}}} =\ Delta E_ {c} ^ {\ Gamma, \ text {L}} + 0,136 \) para apresentar a diferença no Γ - e o ponto L. Assim que o Γ -ponto desce abaixo do ponto L, Δ E _DT será negativo. Uma série de GeNWs tensionados por tração com tamanhos variados são simulados para mostrar a transição direta do bandgap.

Além disso, devido à alta tensão de tração no GeNW, o Γ -valley está abaixo do vale L enquanto os máximos da banda do buraco de luz tornam-se os máximos de valência [28]. O bandgap em tal GeNW de alta tensão será a diferença entre o Γ -valley e os máximos da banda do orifício de luz no Γ -ponto. Assim, o bandgap espacialmente distribuído, bem como as energias da borda da banda no Γ -ponto que é k =0 incluindo banda de condução, banda de orifício pesado e banda de orifício leve são calculados por k.p de oito bandas teoria [29]. Ignoramos o efeito quântico, pois é muito fraco em nosso modelo GeNW com largura basal de 40 nm. O resultado pode ser aplicado para estudar a recombinação elétron-buraco no GeNW tensionado, bem como o mecanismo de aumento da mobilidade. Geralmente, a mobilidade do elétron ou buraco pode ser dada por μ = e τ / m ^∗ , onde m ^∗ é a massa efetiva do portador e τ é o tempo de espalhamento elétron-fônon. No modelo de uma aproximação parabólica para o Γ - e vales L com espalhamento isotrópico, o tempo de espalhamento é proporcional a \ (m_ {DOS} ^ {* - 3/2} \), levando à conclusão de que a razão de mobilidade atinge μ _Γ / μ _L =182 se o Γ -valley move-se abaixo do vale L e tanto o tempo de espalhamento elétron-fônon quanto a massa efetiva dos elétrons são invariáveis ​​com a deformação [30]. No entanto, com a consideração da complexidade no cálculo de espalhamento anisotrópico e massa efetiva dependente de deformação em nosso modelo NW, nós apenas analisamos qualitativamente a melhoria na mobilidade de elétron e buraco em um GeNW altamente tensionado por tração através da diminuição de ambos os elétrons e a massa efetiva do furo no Γ -ponto.

Resultados e discussões

Consideramos que o sistema está inicialmente sob tensão de tração total devido à grande incompatibilidade de rede de 7,7% entre Ge e GaSb. A Figura 2 mostra a distribuição da deformação residual 2D incluindo a deformação no plano ε _xx , tensão de cisalhamento ε _xy , e deformação vertical ε _zz da situação A com a largura de base de w =40 nm, por exemplo, no estado estacionário após o relaxamento. A definição da deformação aqui é ( a _Ges - a _Ge ) / a _Ge , onde a _Ges e a _Ge são constantes de rede de Ge tenso e relaxado, respectivamente. Conforme visto na Fig. 2a, ε _xx tem o valor máximo de cerca de 15,4% nas duas bordas basais que é muito maior do que a deformação inicial, mas diminui drasticamente da borda para o centro com o valor mínimo de cerca de 3,3%. Em z -direcção da parte inferior para a parte superior do GeNW, ε _xx também cai devido ao relaxamento de GeNW. A distribuição de ε _zz tem características semelhantes com ε _xx na Fig. 2b. Ao contrário da deformação biaxial em filme fino de Ge, a Fig. 2c mostra que o componente de deformação de cisalhamento distribuído assimetricamente de GeNW desempenha um papel significativo na transição direta do bandgap. A distribuição da deformação é bastante semelhante em três situações. No entanto, os valores dos componentes de deformação são diferentes em três situações por causa da relação largura-altura diversa ( W / H ) induzida por sua forma. Situação B com GeNW exposto por {105} superfícies tem o maior W / H de 10, exibindo alta tensão semelhante à do filme fino de Ge. Situação C com {111} superfícies expostas também mostra alta deformação, uma vez que a orientação de crescimento NW ao longo de [110] permanece um valor invariável de deformação, aumentando o valor de ε _xx e ε _yy simultaneamente. Assim, a deformação no plano dificilmente pode ser relaxada.

Distribuição da deformação residual de um GeNW na situação A com a largura basal de 40 nm: a deformação do componente x ε _xx , b deformação do componente z ε _zz , e c deformação de cisalhamento no plano x-y ε _xy . A forma em ziguezague na parte inferior denota a camada de substrato parcial (o seguinte tem o mesmo significado)

De acordo com a distribuição de deformações, o incremento de energia de deformações pode ser obtido. Conforme discutido anteriormente, a situação B mantém o maior incremento de energia de deformação, enquanto a situação A possui o menor. No entanto, para a mudança de energia superficial, a situação B fornece valores negativos decrescentes com o aumento da área da seção transversal e as outras duas situações revelam valores positivos muito próximos na mesma área. O incremento de energia total excluindo a mudança de energia de borda é mostrado na Fig. 3a. O resultado mostra que é menos provável formar GeNWs apenas na situação C devido ao incremento de energia nunca ser o menor. Existem duas consequências diferentes do incremento de energia com o aumento da área, e a linha tracejada vertical é marcada para apresentar o valor crítico da área, A _c =136,2 nm ² , o que significa as quantidades de Ge. Quando a área for inferior a 136,2 nm ² , GeNWs tendem a formar a forma na situação B, mas na situação A depois de depositar mais Ge. O resultado do cálculo prevê que GeNWs deformados por tração em GaSb podem preferir formar alto W / H forma de triângulo na seção transversal quando uma pequena quantidade de Ge é depositada, enquanto formando baixo W / H um após exceder o valor crítico. A Figura 3b-e mostra as distribuições da deformação hidrostática e a soma do valor absoluto dos componentes da deformação de cisalhamento na situação A e B sob a área crítica. Comparando a situação A com B, apesar de a situação A possuir o maior valor máximo de deformação hidrostática e | ε _xy | + | ε _yz | + | ε _xz |, a situação B tem maior deformação hidrostática média, mas menor valor médio de | ε _xy | + | ε _yz | + | ε _xz | Enquanto isso, a situação B demonstra uma pequena diferença na distribuição espacial da deformação hidrostática e | ε _xy | + | ε _yz | + | ε _xz | Essas propriedades são muito semelhantes às do filme fino de Ge e são atribuídas ao seu alto W / H valor. Como resultado, referindo-se às Eqs. (5) e (6), a situação B apresenta menor valor de Δ E _DT do que a situação A, levando a uma grande possibilidade de converter Ge em um material bandgap direto.

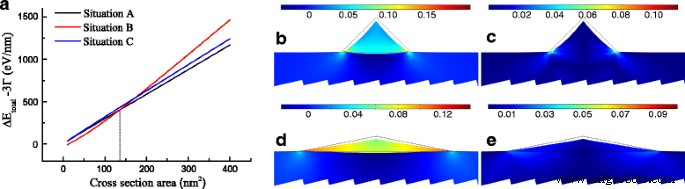
a A mudança de energia total excluindo a mudança de energia de borda 3 Γ vs. a área da seção transversal (a linha tracejada é o valor crítico de mínimos cerca de 136,2 nm ² em diferentes situações). b - e deformação hidrostática e | ε _xy | + | ε _yz | + | ε _xz | em b , c situação A e d , e situação B no valor crítico

Por causa da alta tensão de tração em GeNW, quase toda a região de GeNW pode ser convertida em bandgap direto. A Figura 4a mostra a distribuição de Δ E _DT com o aumento do tamanho do GeNW. O valor de Δ E _DT cai de cima para baixo em GeNWs. Curiosamente, o mínimo de Δ E _DT está localizado na aresta inferior da seção transversal na situação B, mas no centro inferior na situação A. A razão dessa distribuição diferente é que a deformação de cisalhamento significativa na aresta inferior na situação A contribui mais para \ (\ Delta E_ {c} ^ {\ mathrm {L}} \) do que na situação B. Para GeNW na situação B abaixo da área crítica, a média Δ E _DT é muito menor do que na situação A acima da área crítica, conforme mostrado na Fig. 4b. No ponto crítico, a média de Δ E _DT aumenta repentinamente do valor de -0,308 para -0,137 eV. Além disso, para a mesma forma, a distribuição e a média de Δ E _DT são basicamente semelhantes, sem relação óbvia com o tamanho. A fim de descobrir a relação inerente à deformação em GeNW, plotamos o componente de deformação hidrostática na base GeNW com largura basal na Fig. 5. As curvas do componente de deformação hidrostática com tamanhos diferentes versus a posição relativa da base em um GeNW quase se sobrepõem, exceto pela diferença na região periférica. As consequências consistentes são encontradas em ε _xx e a soma dos componentes absolutos de cisalhamento. Assim, o valor induzido por deformação de Δ E _DT possui a distribuição idêntica em GeNW com a mesma forma.

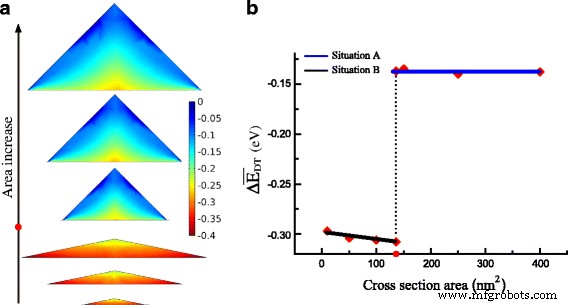
a A distribuição de Δ E _DT com aumento da área (a barra de cores denota o valor de Δ E _DT ) b A média de Δ E _DT vs. a área. O valor crítico é marcado com ponto vermelho no eixo da área

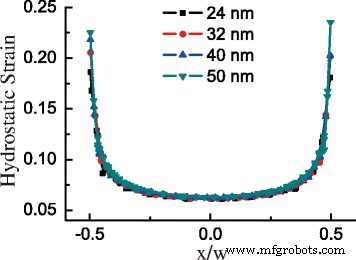
Componente de deformação hidrostática na base de GeNW vs. x / w com diferentes larguras basais

Além disso, simulamos o mapeamento de bandgap induzido por deformação na seção transversal do GeNW de 40 nm mostrado na Fig. 6a. A distribuição espacial de bandgap é derivada do valor variável das bordas de banda dependentes de deformação no Γ -ponto. A Figura 6b exibe a energia da borda da banda em Γ -ponto ao longo do z -direcção do GeNW. Descobrimos que tanto a banda de condução quanto as bordas da banda de valência, incluindo a banda do orifício leve e a banda do orifício pesado, mudam significativamente nos primeiros 15 nm e depois ligeiramente. Os topos da faixa do orifício leve e pesado se separam e tendem a se deslocar em direções opostas com o aumento da tensão de tração. Da Fig. 6a, b, o bandgap aumenta significativamente nos primeiros 15 nm para atingir cerca de 0,30 eV, então muda ligeiramente em torno de um valor de 0,24 eV, que é o bandgap na maioria das regiões GeNW. Uma vez que o máximo da banda do orifício leve é ​​maior do que o da banda do orifício pesado no Γ - ponto no GeNW, os furos na banda de valência preferem situar-se nos máximos da banda do furo leve. Assim, a recombinação elétron-buraco ocorrerá entre a banda de condução mínima e a banda de buraco de luz máxima no Γ -ponto se negligenciarmos a sobreposição do elétron dependente do espaço e funções de onda de buraco. Curiosamente, os máximos da banda do orifício de luz se movem mesmo acima dos mínimos da banda de condução na região do fundo NW marcada como uma curva preta na Fig. 6a com deformação hidrostática superior a ∼5,0%. O bandgap negativo que calculamos sob alta tensão de tração pode causar consequências complicadas, como estrutura de banda semimetálica [31] ou invertida [32].

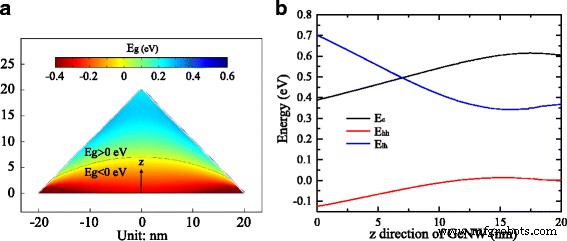
a O bandgap dependente da deformação no GeNW distribuído por posições. b As energias da borda da banda dependentes de deformação ao longo de z direção no GeNW

Finalmente, a mobilidade dos elétrons e buracos será aumentada sob tal tensão altamente tênsil no GeNW. Para o Ge relaxado, o transporte de elétrons é principalmente fornecido por elétrons domiciliados no vale-L. Quando Ge está sob tensão de tração para que o Γ -valley está abaixo do vale L, como mostrado na Fig. 3a, a contribuição primária do transporte de elétrons é do Γ -vale. Por outro lado, a participação dominante dos furos no transporte é da faixa do furo leve no Γ -ponto sob alta tensão de tração, enquanto a banda de orifício pesado ocupa os máximos da banda de valência no caso relaxado. Devido à massa efetiva do elétron muito menor no Γ -ponto do que no ponto L, bem como a massa efetiva diminuída dos máximos da banda do buraco pesado para os máximos da banda do buraco leve, a mobilidade não apenas dos elétrons, mas também dos buracos pode ser aumentada. A deformação de tração pode ser prevista teoricamente para reduzir a massa efetiva de elétrons e buracos no Γ -ponto em um modelo de ponto quântico por Califano e Harrison [29]. Embora o método de cálculo quantitativo seja inadequado para nosso modelo NW, assumimos qualitativamente que a deformação de tração pode modificar a massa efetiva em k =0 aumentando a curvatura da relação de dispersão para pequenos k nas proximidades do Γ -ponto. Assim, a mobilidade de elétrons e lacunas pode ser aumentada em GeNWs tensionados por tração. As bandas de valência de divisão também induzem forte acoplamento elétron-fônon e espalhamento intrabanda [33], o que limita a mobilidade do buraco a ser menor do que a mobilidade do elétron.

Conclusões

Em resumo, propusemos GeNWs deformados por tração em GaSb, comparando três situações diferentes por meio da mudança total de energia antes e depois da deposição de Ge. O resultado mostra que o GeNW é inclinado a formar {105} superfícies ao longo da direção de crescimento de 〈100〉 antes da quantidade crítica, enquanto exposto por {110} superfícies após a quantidade crítica. O campo de deformação residual e a análise de bandgap mostraram que a mesma forma tem uma distribuição semelhante tanto na deformação quanto Δ E _DT independentemente do tamanho. Além disso, a deformação no plano e a deformação hidrostática reduzem não apenas das bordas para o centro, mas também de baixo para cima em todas as situações. Devido à alta tensão de tração, quase todo o GeNW em GaSb pode ser convertido em um material bandgap direto nas duas situações possíveis. Além disso, os buracos de luz participam principalmente da recombinação elétron-buraco e do transporte elétrico no Γ -ponto porque os máximos da banda do orifício leve tornam-se os máximos da banda de valência em deformação altamente tênsil. A mobilidade não apenas de elétrons, mas também de lacunas pode ser aumentada devido à diminuição da massa efetiva do portador no Γ -ponto determinado pela deformação de tração. O desempenho atrativo previsto teoricamente implica que GeNWs tensionados por tração são promissores para aplicação em optoeletrônica para fonte de luz e microeletrônica para dispositivos de alta velocidade em fotônica de Si e eletrônica, respectivamente.

Propriedades das oscilações eletromagnéticas longitudinais em metais e sua excitação em superfícies planas e esféricas Propriedades elétricas de materiais compostos com alinhamento assistido por campo elétrico de cargas de nanocarbono