Uma bomba d'água nanométrica induzida pelo movimento browniano e não browniano de uma folha de grafeno em uma superfície de membrana

Resumo

Bomba de água com economia de energia e membranas semipermeáveis eficientes são os núcleos da tecnologia de osmose reversa. Aplicar nanotecnologia para melhorar o desempenho está na moda nos últimos anos. Com base no efeito competitivo da infiltração espontânea da água de dois lados de um nanotubo de carbono, projetamos uma bomba de água que faz uso da permeabilidade natural, enfraquecendo a competitividade de um lado com base em uma pequena folha de grafite colocada na membrana. De acordo com as simulações de dinâmica molecular, o fluxo líquido contínuo é observado. O modo de movimento da folha é a chave para a performance. Para o movimento browniano puro sem nenhuma carga dinâmica, encontramos duas moléculas de água por fluxo de nanossegundo, enquanto o fluxo induzido pelo movimento unidirecional pode ser várias vezes aumentado, dependendo da força externa. O movimento browniano é semelhante ao mecanismo físico de pressão osmótica, e o movimento unidirecional apresenta ótimo desempenho que possui enormes aplicações para osmose reversa. Nosso trabalho propõe de forma criativa uma nova estratégia para bombear moléculas de água cruzando um nanocanal, inspirando para designers de dispositivos nanofluídicos.

Histórico

A dessalinização da água do mar é um sinalizador para resolver a escassez global de água, pois pode oferecer água limpa infinita em teoria. No entanto, a tecnologia atual não é perfeita. Existem dois métodos diferentes para a dessalinização da água do mar. A primeira é a destilação, obtendo água pura por meio do aquecimento da água do mar e, em seguida, resfriando os vapores. A mudança de fase pode remover totalmente as impurezas, mas com uso intensivo de energia e caro. O outro é a osmose reversa (RO), conduzindo a água do mar através de uma membrana semipermeável que é permeável à água, mas impermeável aos íons. Benefícios do aprimoramento de membranas semipermeáveis e bombas de água de pressão, o RO é maduro e amplamente utilizado [1]. No entanto, RO ainda consome muita energia [2,3,4]. Isso ocorre porque o sistema RO precisa manter uma alta queda de pressão para compensar a pressão permeável e conduzir a água do mar através das membranas semipermeáveis. Muitos cientistas acreditam que “para que a dessalinização corresponda aos desafios da água do século 21, é necessária uma mudança radical na tecnologia de membrana RO” [5]. Eles propõem que os nanotubos de carbono (CNTs) são um canal de água ideal com as vantagens de seletividade, alta eficiência e baixo custo de energia [6] e têm grande potencial para aplicações como canais nanofluídicos [7,8,9,10]. No entanto, apenas melhorar a propriedade da membrana RO é útil para a eficácia do RO, mas inútil para economizar energia, pois a dessalinização RO atual já está perto da limitação termodinâmica [4]. Métodos de acionamento mais eficientes são necessários como alternativas à bomba de alta pressão [11].

Para um canal de CNT conectando dois reservatórios de água, as moléculas de água sempre podem entrar no canal espontaneamente devido ao movimento browniano. No entanto, os efeitos de infiltração de dois lados do canal CNT compensam um ao outro, uma vez que não existe fluxo líquido de água. Como o fluxo líquido é considerado pelo resultado da competição do movimento browniano de dois lados do canal CNT, aumentar ou enfraquecer a competitividade de um lado deve ser um método eficaz para bombear água. Em trabalhos anteriores, a queda de pressão [12, 13], a diferença de temperatura [14, 15] e o campo elétrico [16] são estratégias comuns para aumentar a competitividade de um lado para criar fluxo líquido de água. No entanto, enfraquecer a competitividade parece ser uma escolha mais acertada à medida que utilizamos a permeabilidade natural.

Na verdade, controlar o transporte nanofluídico é relevante para aplicações generalizadas, que vão desde armazenamento de energia até biossensores [17,18,19,20,21,22,23], o que ainda é um desafio. Aqui, projetamos uma nova bomba d'água com uma pequena folha de grafite em um lado da membrana com o objetivo de quebrar o equilíbrio do movimento browniano dos dois reservatórios, assemelhando-se a um sistema de quebra simétrico. A folha possui dois modos de movimento:movimento térmico e movimento unidirecional, correspondendo a movimentos brownianos e não brownianos, respectivamente. Por meio de cálculos de simulação, o enfraquecimento da competitividade da parte superior é alcançado e um fluxo de água descendente é induzido. Além disso, para o movimento browniano, a quantidade de fluxo de água é de quase dois por nanosegundo que se aproxima da aquaporina [24, 25], sugerindo possíveis aplicações em membranas biológicas. A pequena lâmina conduz a água de baixo para cima através do CNT, o que pode ser uma analogia ao mecanismo físico de pressão osmótica. Além disso, no movimento unidirecional, a quantidade de fluxo pode ser significativamente aumentada várias vezes, dependendo da velocidade de movimento da folha ou da força externa. Conforme a tecnologia entra em operação em escala molecular, como a manipulação de nanopartículas de superfície por pinças ópticas [26] e microscopia de força atômica [27], nosso trabalho apresenta uma probabilidade de ajustar a simetria de permeação de água, o que abre um novo método para bomba d'água.

Método de modelo e simulação

Um instantâneo do sistema de simulação é mostrado na Fig. 1. Usamos um (6, 6) CNT (comprimento de 2,56 nm e diâmetro de 0,81 nm) e duas folhas de grafite paralelas (5,1 × 5,1 nm ² ) para compor uma membrana permeável. Em tal canal estreito, as moléculas de água exibem um arranjo de arquivo único [6]. Uma pequena folha de grafite composta de 272 átomos de carbono é colocada próxima à membrana. A forte interação carbono-carbono leva à adsorção de uma pequena folha na membrana. Na verdade, durante o processo de nossas simulações, a distância média da folha e da membrana é de cerca de 0,34 nm. No movimento browniano, definimos a temperatura da pequena folha de grafite variando de 100 a 500 K. Ela oscilará na membrana perto da entrada do CNT, colidindo com as moléculas de água próximas. Três mil trezentos e vinte e oito moléculas de água enchem o canal e dois reservatórios. A temperatura da água é fixada em 300 K. Para o modo de movimento unidirecional, aplicamos uma aceleração adicional em cada átomo de carbono da pequena folha para atingir a força adicional, onde 0,1 nm / ps ² corresponde a 2 pN. A força adicional está ao longo de x direção. O fluxo de água é induzido pela assimetria do sistema. Devido à condição de contorno periódica em todas as três dimensões, a folha estará passando continuamente nas proximidades da entrada do CNT e induz fluxo e fluxo de água estáveis.

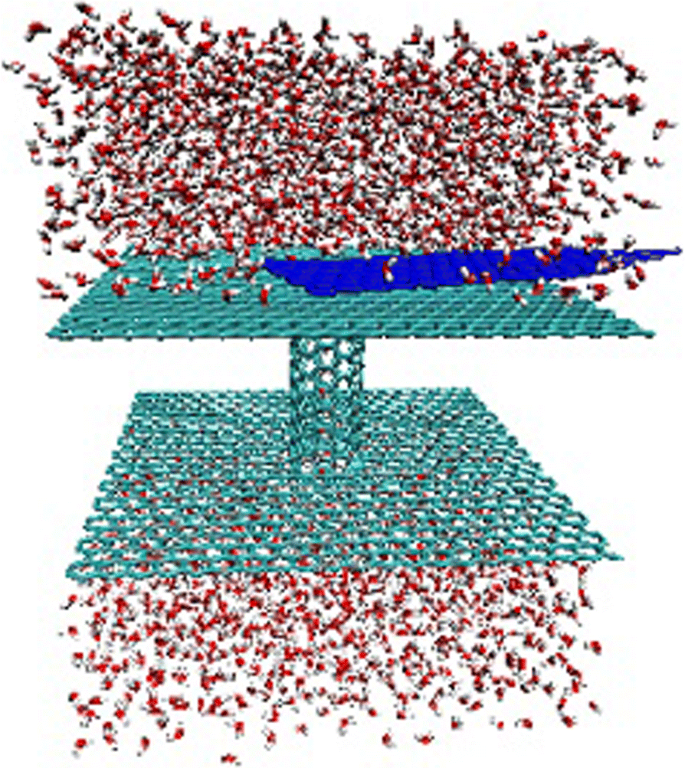
Instantâneo do sistema de simulação. Um CNT com comprimento de 2,56 nm e diâmetro de 0,81 nm, conectando dois reservatórios de água, separados por duas folhas de grafite (verde sálvia, 5,1 × 5,1 nm ² ) Uma pequena folha de grafite (azul) colocada na grande de perto. O sistema foi embutido em uma caixa d'água periódica com 3328 moléculas de água, representando uma bomba d'água nanométrica

Durante nossas simulações, o sistema estava em um volume e temperatura constantes com caixa periódica, e as moléculas de água eram modelos clássicos TIP3P [28]. Os átomos de carbono eram partículas de Lennard-Jones (LJ) sem carga com parâmetros de σ _cc =0,34 nm, ε _cc =0,3612 kJ / mol; σ _co =0,3275 nm, ε _co =0,4802 kJ / mol [6]. O método PME foi empregado para lidar com as interações eletrostáticas de longo alcance [29]. As simulações rodam 125 ns no software Gromacs 4.6.5 [30] com um intervalo de tempo de 2 fs (dados coletados a cada 1 ps), e os últimos 120 ns foram coletados. Duas simulações independentes foram feitas para reduzir o erro.

Resultados e discussão

O movimento browniano de uma folha de grafite

Primeiramente, estudamos o modo de movimento browniano da folha em diferentes temperaturas. Para medir a capacidade de induzir o fluxo de água através dos CNTs, seguindo o trabalho anterior [31, 32], definimos o fluxo ascendente e o fluxo descendente como a quantidade de moléculas de água conduzindo através do tubo ao longo do + z e - z direção, respectivamente. Fluxo =fluxo ascendente + fluxo descendente, fluxo =fluxo ascendente - fluxo descendente e eficiência de transporte unidirecional η pode ser calculado por η =Fluxo / fluxo. O fluxo e o fluxo de água em função da temperatura da folha são mostrados na Fig. 2. Em nossa hipótese original, a folha quente aquece a água ao redor e então cria uma diferença de temperatura ao longo do CNT para conduzir a água através do canal. No entanto, o fluxo de água nas simulações é de baixo para cima, o que se opõe ao que esperávamos. Além disso, o fluxo de água é insensível à temperatura da folha. Além disso, a flutuação de temperatura de uma pequena folha está dentro do escopo de 10 K durante nosso processo de simulação. Na verdade, devido ao controle de temperatura das simulações NVT, a troca de calor entre a folha e a solução circundante é fraca e pode ser ignorada. Como mostra a Fig. 2, podemos sempre obter fluxo líquido contínuo em cerca de duas moléculas de água por nanossegundo, independentemente da temperatura da folha, que está perto do valor experimental de 1,8 em canais de aquaporina [24, 25], sugerindo aplicações potenciais em sistemas biológicos. Enquanto isso, o fluxo total de água é quase independente da temperatura da folha e deve ser semelhante ao caso sem folha.

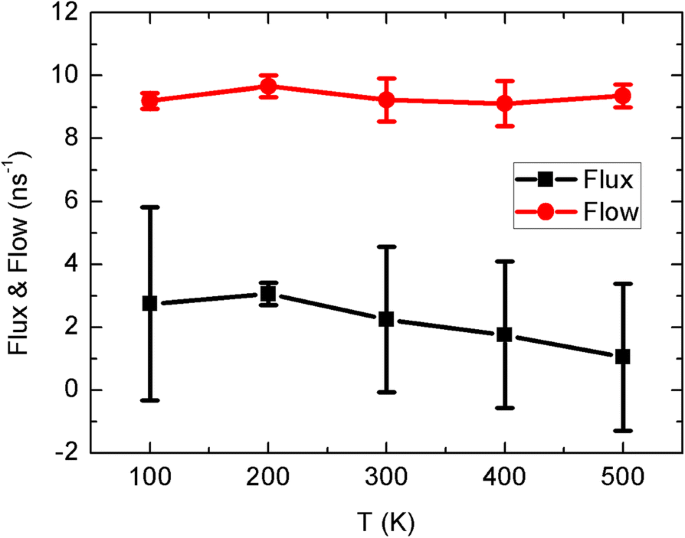
Fluxo e vazão da água em função da temperatura da folha. Barras de erro são mostradas para dois pontos de dados

A polarização do transporte de água pelo movimento browniano de uma nanofolha assemelha-se ao processo osmótico. Do ponto de vista da dinâmica molecular, o fluxo líquido de água deve ser causado pela competição do movimento browniano das moléculas de água perto das duas entradas do canal CNT. O pequeno lençol influencia a velocidade das moléculas de água por colisões frequentes e, em seguida, altera a competitividade. Curiosamente, a folha é colocada na parte superior, mas induz o fluxo de água ascendente, sugerindo que o efeito da folha está enfraquecendo a competitividade. No entanto, o movimento browniano da folha é irregular e o fluxo líquido é insensível à temperatura com grande flutuação. Conseqüentemente, discutiremos mais detalhadamente o modo de movimento unidirecional da folha na próxima parte, e fenômenos mais interessantes serão descobertos.

Em seguida, reunimos o tempo de translocação da água e a ocupação, conforme mostrado na Fig. 3. Aqui, o tempo de translocação é o tempo médio de trânsito para as moléculas de água através do canal de CNT. Semelhante ao fluxo de água, o tempo de translocação flutua com a temperatura da folha. Na verdade, o tempo de translocação deve corresponder ao fluxo de água, pois quanto mais rapidamente as moléculas de água passam pelo canal, maior deve ser o fluxo de água. No entanto, tal anti-relação é coberta pela flutuação termodinâmica aqui. Em teoria, a ocupação é determinada pela estrutura do canal CNT. Como a cadeia de água em fila única é mantida, sempre há quase dez moléculas de água dentro do canal CNT com pequenas flutuações. Conseqüentemente, as flutuações termodinâmicas são inevitáveis, mas não notáveis.

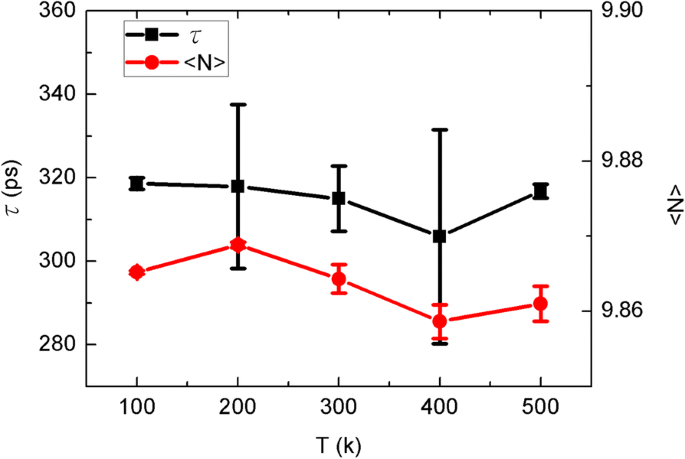
O tempo de translocação da água τ e ocupação < N > em função da temperatura da folha

Como as propriedades de dinâmica térmica das moléculas de água dentro do CNT estreito é outra questão importante que nos preocupa, as distribuições de densidade e o número de ligações de hidrogênio (ligação H) são contados como uma função de z posição exibida na Fig. 4. Aqui, as duas moléculas de água formam uma ligação H quando sua distância de oxigênio é menor que 0,35 nm e o ângulo entre a ligação O – H e O – O é menor que 30 °. A parte 2–4 nm de z A posição corresponde ao canal CNT, onde o comportamento da densidade e do número de ligação H é diferente das áreas a granel. A densidade no CNT é quase quatro vezes maior que no volume, implicando no potencial de armazenamento em massa. O padrão ondulatório de densidade com dez picos está alinhado com a ocupação na Fig. 3, devido à estrutura única do CNT. A alteração do número da ligação H também exibe o processo de uma molécula de água entrando no CNT para formar uma cadeia de arquivo único com ligações H reduzidas.

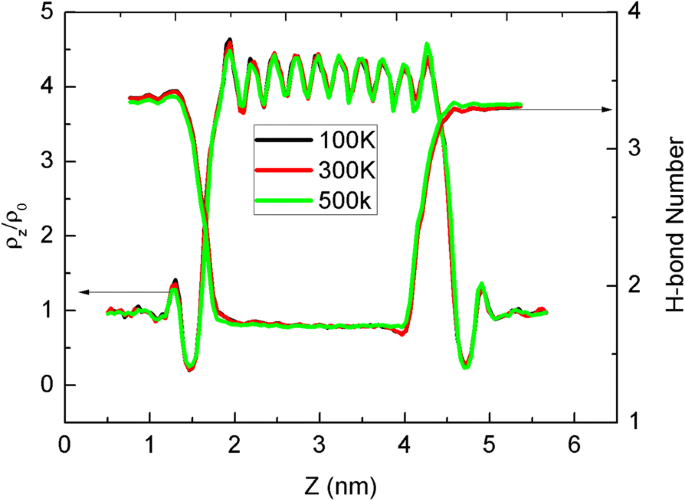
Distribuição do número da densidade e da ligação de hidrogênio ao longo de z eixos e cores de linha diferentes são para temperaturas de folha diferentes. Aqui, ρ ₀ é 1,0 g / cm ³ da densidade da água

Moléculas de água dentro do CNT com orientações únicas foram reveladas anteriormente [16]. Aqui, calculamos a distribuição de probabilidade das orientações água-dipolo, conforme mostrado na Fig. 5. Para reduzir o erro, calculamos a média dos dados das duas simulações independentes. <θ> é o ângulo médio entre o dipolo da água e o z eixo, e há quase dois estados (20 ° –40 ° e 140 ° –160 °) para as orientações da água. O padrão é quase simétrico em relação a <θ> =90 °, indicando a orientação única do dipolo. Como um todo, o transporte de água é insensível à temperatura da folha. Isso ocorre porque o movimento browniano da folha está sempre na membrana de grafeno devido à forte interação hidrofóbica folha-membrana, e o impacto da folha é muito limitado. A seguir, discutiremos mais detalhadamente o modo de movimento unidirecional da lâmina, onde o transporte de água pode ser afetado de forma mais significativa.

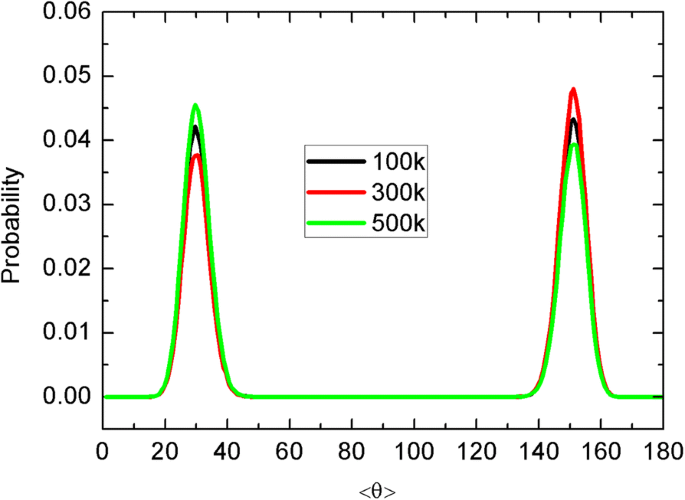
A distribuição de probabilidade da orientação dipolar média das moléculas de água dentro do CNT e as diferentes temperaturas da folha são marcadas por linhas de cores

O movimento unidirecional de uma folha de grafite

Como o movimento da folha deve ser importante para o desempenho, investigamos ainda um modo de movimento não browniano típico, ou seja, o movimento unidirecional. A folha é impulsionada por uma força adicional e se move na membrana de grafeno com velocidade estável. Curiosamente, o fluxo de água, fluxo e eficiência de transporte unidirecional η aumenta rapidamente com o aumento da força, conforme visto na Fig. 6a. Em seguida, para descrever a dinâmica da folha, apresentamos a equação de Langevin unidimensional:
$$ m \ frac {d ^ 2x} {\ mathrm {d} {\ mathrm {t}} ^ 2} =F- m \ xi \ frac {\ mathrm {d} \ mathrm {x}} {\ mathrm { d} \ mathrm {t}} + R (t) $$
onde, m é a massa da folha, F é a força motriz, R ( t ) é a força causada pelas colisões aleatórias de moléculas de água, e ξ é o coeficiente de atrito. As colisões aleatórias são complicadas, e aqui, nós apenas contamos R ( t ) como as colisões mutuamente compensadas e < R ( t )> =0. No estado estacionário, a folha mantém uma velocidade uniforme e a força de atrito é igual à força motriz. Por isso,
$$ F =m \ xi \ frac {\ mathrm {dx}} {\ mathrm {dt}} =m \ xi v $$

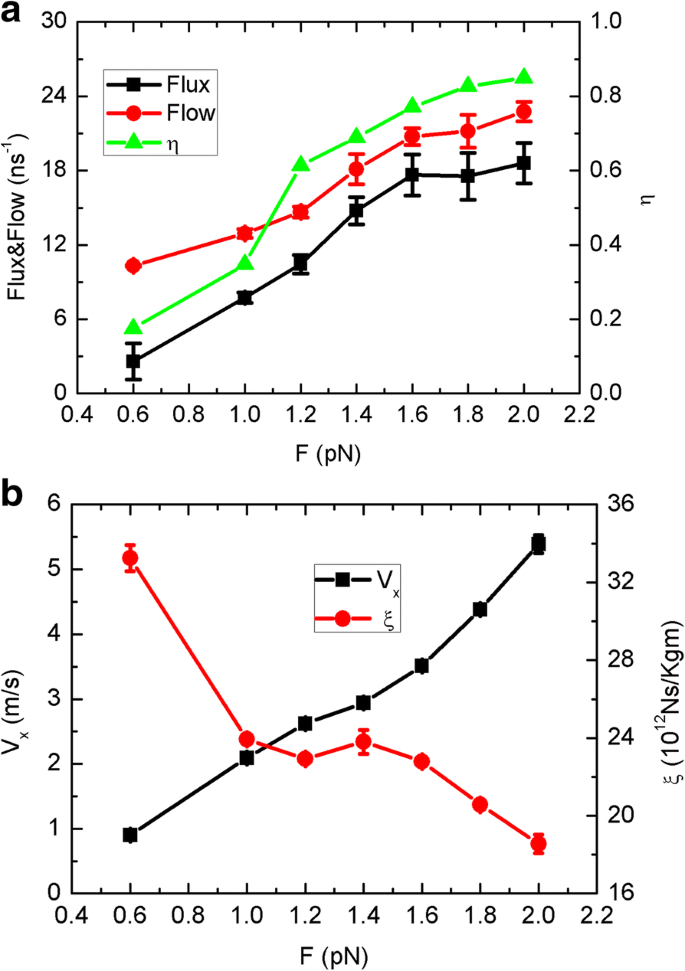
a O fluxo de água, fluxo e eficiência unidirecional η e b a velocidade da folha V _x e coeficiente de atrito ξ em função da força motriz F

Exibimos a velocidade (da trajetória MD) e o coeficiente de atrito ξ em função da força motriz na Fig. 6b. A velocidade aumenta quase linearmente com a força motriz, correspondendo aos comportamentos de fluxo e fluxo, enquanto o coeficiente de atrito diminui como um todo. Assim, a vazão e o fluxo de água devem estar diretamente relacionados à velocidade da folha. Na visão da dinâmica molecular, como o efeito competitivo existe, a lâmina arrasta as moléculas de água circundantes e enfraquece a competitividade do lado superior. Quanto mais rápido a folha se move, mais fraca deve ser a competitividade. Como a força excede 1,6 pN, o fluxo tende a ser suave, próximo a 16 por nanossegundo, que é quase 8 vezes o modo browniano. Obviamente, esse movimento unidirecional é mais eficiente do que o movimento browniano aleatório. Portanto, a lâmina controlada artificialmente é outra estratégia alternativa para osmose reversa, onde a lâmina poderia ser manipulada por algumas tecnologias experimentais avançadas, como pinças ópticas [26] e microscopia de força atômica [27].

Notavelmente, o aumento da velocidade da folha e da força motriz levou ao enfraquecimento da competição do lado superior muito mais do que o modo browniano. Em um esforço para elucidar ainda mais como o deslocamento da água é afetado, exibimos o tempo médio de translocação e a ocupação como uma função da força motriz na Fig. 7. Ambos mostram relações quase lineares com a força motriz, diferindo dos resultados de Fig. 3. A diminuição do tempo de translocação corresponde ao comportamento crescente do fluxo de água na Fig. 6a, que deve ser causado pelo arrasto da folha. De outro ponto de vista, quando a lâmina se arrasta ao redor das moléculas de água, a competitividade térmica do lado superior deve ser reduzida, facilitando a penetração de água de baixo para cima pelo canal de CNT.

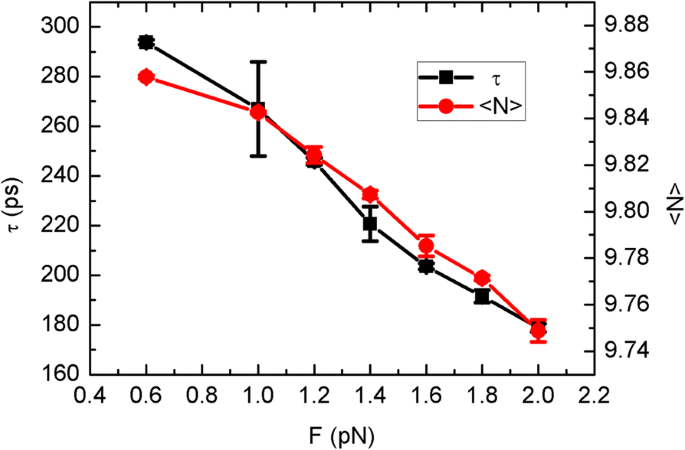
O tempo de translocação τ e ocupação < N > em função da força motriz

Apresentamos ainda os perfis de densidade de água, ligação H e distribuições de dipolo de água na Fig. 8. Como pode ser visto na Fig. 8a, os perfis de densidade e ligação H são apenas ligeiramente afetados pelo movimento da folha. Por exemplo, sob a grande força de 1,8 pN, os picos de densidade semelhantes a ondas tornam-se reduzidos e a distribuição da ligação H torna-se ligeiramente assimétrica. Mudança semelhante pode ser encontrada para a orientação do dipolo de água na Fig. 8b. Sob a condição de equilíbrio, por exemplo, para o movimento browniano acima, os dois eventos de orientação acontecem com probabilidade semelhante, levando à altura de pico semelhante, como visto na Fig. 5. No entanto, como discutimos, o movimento unidirecional da folha deve têm mais influência na cadeia de água do que o movimento browniano. Isso ocorre porque a lâmina que flui arrastará a água circundante para se mover devido à interação lâmina-água de Lennard-Jones e, portanto, afetará o movimento ou a orientação da água perto da entrada do CNT. Portanto, as orientações dipolo na Fig. 8b tornam-se assimétricas. Embora a dinâmica e a termodinâmica da água confinada possam ser perturbadas mais profundamente para o movimento unidirecional, devido à preservação da cadeia de água em fila única, tal perturbação ainda é muito limitada, especialmente para a termodinâmica e as principais características de densidade, ligação H , e dipolo estão próximos ao caso do movimento browniano. Consequentemente, diferentes modos de movimento da folha podem ter um impacto maior na dinâmica da água do que na termodinâmica.

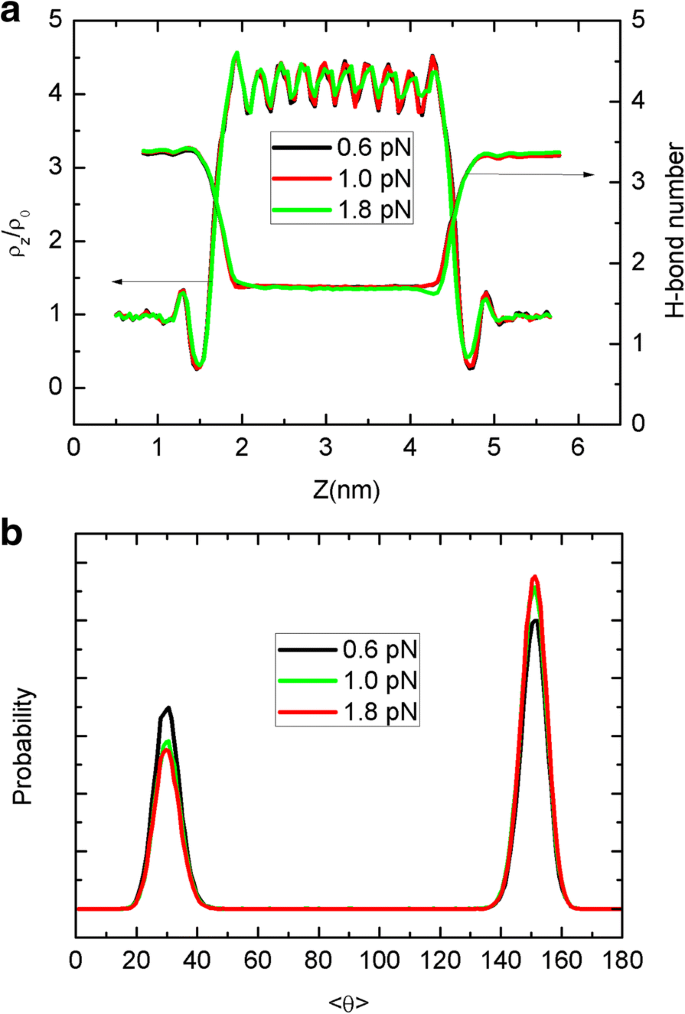
a Os perfis de densidade axial da água e o número da ligação de hidrogênio em função de z posição ao longo do CNT para forças diferentes. b Distribuição de probabilidade da orientação dipolar média das moléculas de água dentro do CNT para diferentes forças

Discussão adicional

Acredita-se que a distância inicial entre a folha de grafeno e a entrada do CNT deva ter um efeito trivial no fluxo de água e no fluxo através do CNT. Na verdade, colocamos aleatoriamente a folha na membrana de grafeno superior, onde a folha é diretamente adsorvida na superfície sem qualquer água no meio, como visto na Fig. 1 acima. Desta forma, a folha sempre se moverá na superfície por causa da forte interação hidrofóbica folha-membrana, proporcionando um sistema nanofluídico assimétrico. Conforme mostrado na Fig. 9, calculamos a distância média folha-membrana e folha-CNT para os movimentos browniano e unidirecional. É surpreendente que a distância média folha-membrana seja fixada em 0,34 nm para ambos os casos, correspondendo estritamente ao diâmetro potencial de Lennard-Jones carbono-carbono. Assim, a folha estará sempre adsorvida na superfície da membrana. Para o movimento browniano na Fig. 9a, a distância da folha-CNT também é uma constante que é independente da temperatura da folha. Isto é claramente devido à interação hidrofóbica folha-CNT que leva ao círculo da folha em relação ao CNT. Devemos também notar que em nossa configuração de simulação, a entrada do CNT excede a localização da membrana de grafeno 0,2 nm, e isso pode evitar que a entrada seja bloqueada pela folha. Acredita-se que se a folha não for colocada inicialmente na membrana, ela pode se mover no reservatório de forma aleatória e deve ter alguma probabilidade de bloquear a entrada do CNT. Além disso, para o movimento unidirecional na Fig. 9b, a distância da folha-CNT exibe comportamentos crescentes com o aumento da força, correspondendo aos comportamentos de fluxo e fluxo. Com pouca força, a folha pode ficar realmente presa perto do CNT por um tempo, enquanto a força maior pode acelerar a passagem da folha, levando a uma distância maior. Excessivamente, a distância inicial da folha-CNT não deve ter efeito apreciável no fluxo e fluxo de água, enquanto a folha-membrana poderia ter. No entanto, se a folha estiver inicialmente em água bruta em vez de na membrana, o sistema deve se tornar simétrico, o que difere de nosso objetivo inicial, e o fenômeno de transporte de polarização deve desaparecer.

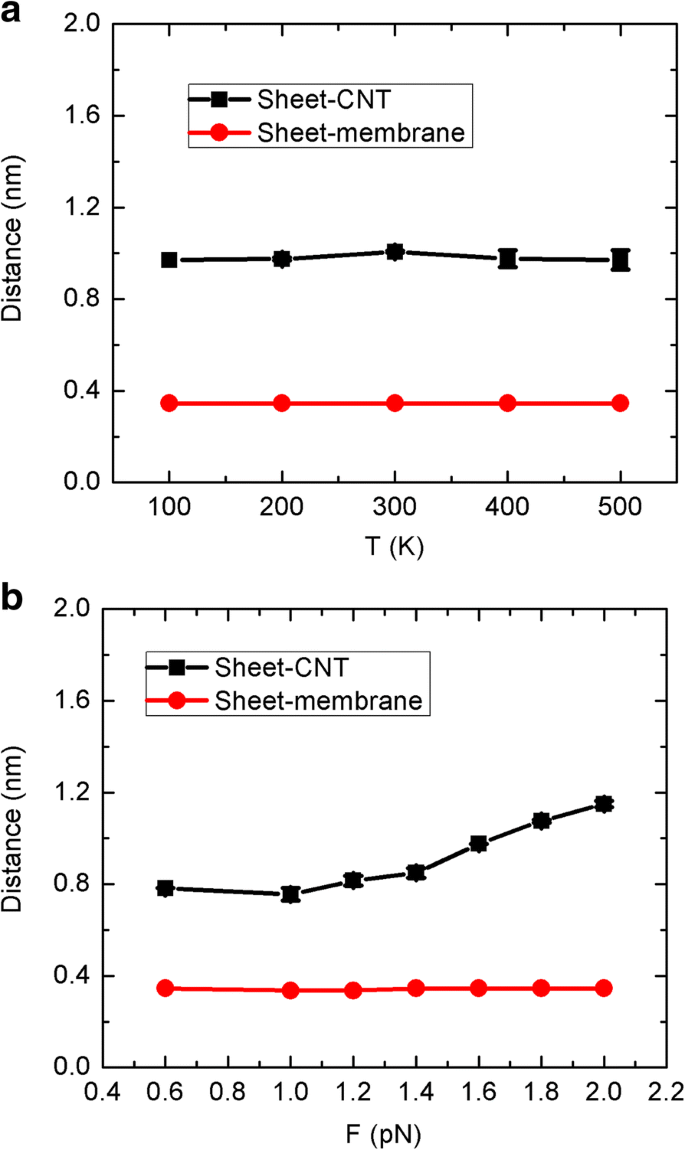
A distância média de folha-membrana e folha-CNT para diferentes condições de simulação: a Movimento browniano e b movimento unidirecional

Para o movimento browniano, as temperaturas médias da água e da folha durante o processo de simulação são mostradas na Fig. 10 como uma função da temperatura alvo da folha. Podemos ver que a temperatura média da folha pode ser estritamente controlada em seus valores alvo e, da mesma forma, o valor médio da água também é mantido em T =300 K. Na verdade, usamos o método Nose-Hoover para controlar as temperaturas da lâmina e da água. Geralmente, nos conjuntos NVT (ou NPT) de simulações de MD, a troca de calor entre diferentes moléculas não pode acontecer por causa do termostato. No entanto, as colisões intermoleculares entre a lâmina e a água circundante devem sair, mesmo que sejam finalmente ajustadas pelo termostato. As colisões da folha em movimento podem afetar a velocidade instantânea ou a direção das moléculas de água circundantes e, assim, em última análise, alterar a probabilidade de a água entrar no CNT. No entanto, ainda é muito difícil captar tal influência instantânea do lençol sobre a água, já que deve acontecer em um tempo muito curto, possivelmente menos do que o tempo de coleta de dados de 1 ps. Assim, podemos hipotetizar que a vibração da chapa pode afetar a flutuação térmica da água circundante e enfraquecer a competitividade do reservatório superior, levando ao fenômeno de transporte de polarização.

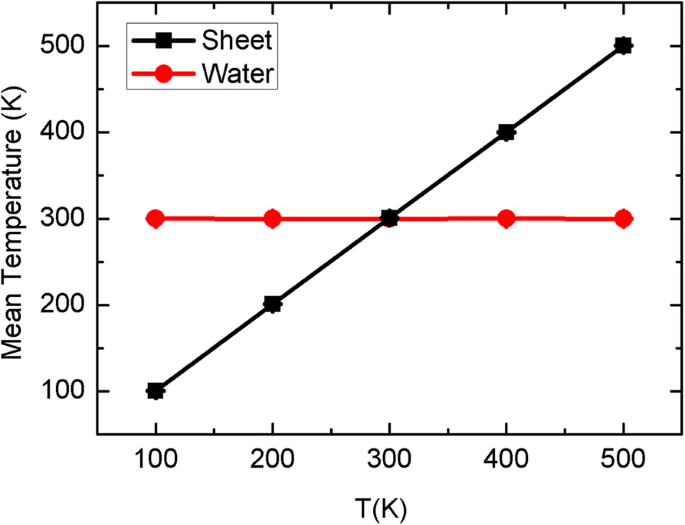
As temperaturas médias da folha e da água em função da temperatura alvo da folha

Conclusões

Em resumo, propusemos uma nova estratégia para simulações dinâmicas de bomba de água por molécula e obtivemos um fluxo líquido de água considerável com base na permeabilidade espontânea da água. As moléculas de água entram no canal CNT de forma inicial devido ao movimento browniano, enquanto dois lados do CNT competem entre si e se deslocam. Em nossa pesquisa, uma pequena folha se movendo na membrana enfraquece a competitividade de um lado e induz fluxo líquido contínuo. Durante as simulações, descobrimos que o modo de movimento da folha é a chave para o desempenho. O movimento browniano puro induz um pequeno fluxo líquido estável de água em torno de 2 ns ⁻¹ isto é independente da temperatura da folha, enquanto o movimento unidirecional pode criar um fluxo significativamente maior, dependendo da força motriz na folha. Além disso, com o aumento da força motriz, o tempo de translocação da água reduz linearmente, correspondendo ao fluxo de água ou comportamento do fluxo. Excessivamente, o movimento unidirecional tem um impacto maior na dinâmica e na termodinâmica da água. Consequentemente, apresentamos de forma criativa o uso da permeabilidade da água da natureza, obtida por uma pequena folha de grafite colocada na membrana, o que seria útil para a tecnologia de RO.

Abreviações

CNT:: Nanotubo de carbono
MD:: Dinâmica Molecular
RO:: Osmose Inversa

Desempenho fotovoltaico de células solares de nanocone de junção de pinos com absorção ótica efetiva aprimorada O efeito da apoptose nas células cancerosas do fígado de nanopartículas de ouro modificadas com ácido litocólico

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias