Máquinas de estado finito

Até agora, todo circuito apresentado era um combinatório o circuito. Isso significa que sua saída depende apenas de suas entradas atuais. As entradas anteriores para esse tipo de circuito não têm efeito na saída.

No entanto, existem muitas aplicações em que é necessário que nossos circuitos tenham “memória”; para lembrar entradas anteriores e calcular suas saídas de acordo com elas. Um circuito cuja saída depende não apenas da entrada atual, mas também do histórico da entrada é chamado de circuito sequencial .

Nesta seção, aprenderemos como projetar e construir tais circuitos sequenciais. Para ver como funciona esse procedimento, usaremos um exemplo, no qual estudaremos nosso tema.

Então, vamos supor que temos um jogo de teste digital que funciona em um relógio e lê uma entrada de um botão manual. No entanto, queremos que o switch transmita apenas um pulso HIGH para o circuito. Se prendermos o botão diretamente no circuito de jogo, ele transmitirá ALTO pelo menor número de ciclos de clock que nosso dedo conseguir. Em uma frequência de relógio comum, nosso dedo nunca pode ser rápido o suficiente.

O procedimento de design tem etapas específicas que devem ser seguidas a fim de realizar o trabalho:

Etapa 1

A primeira etapa do procedimento de design é definir com palavras simples, mas claras, o que queremos que nosso circuito faça:

“Nossa missão é projetar um circuito secundário que transmitirá um pulso ALTO com duração de apenas um ciclo quando o botão manual for pressionado, e não transmitirá outro pulso até que o botão seja pressionado e pressionado novamente.”

Etapa 2

A próxima etapa é projetar um diagrama de estado.

Este é um diagrama feito de círculos e setas e descreve visualmente o funcionamento do nosso circuito. Em termos matemáticos, este diagrama que descreve a operação de nosso circuito sequencial é uma Máquina de Estados Finitos. Observe que esta é uma máquina de estados finitos Moore.

Sua saída é uma função apenas de seu estado atual, não de sua entrada. Isso está em contraste com a Mealy Finite State Machine, onde a entrada afeta a saída. Neste tutorial, apenas a Máquina de Estados Finitos Moore será examinada.

O diagrama de estado do nosso circuito é o seguinte:(Figura abaixo)

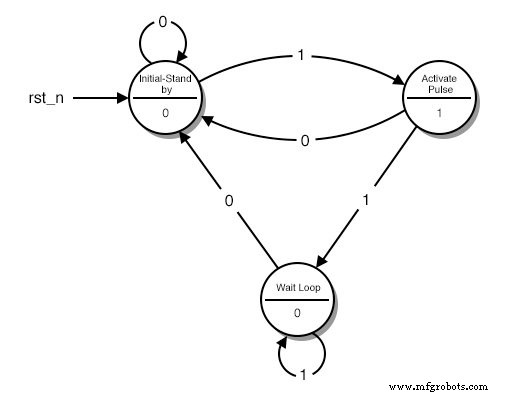
Um diagrama de estado



Cada círculo representa um “estado”, uma condição bem definida em que nossa máquina pode ser encontrada. Na metade superior do círculo, descrevemos essa condição. A descrição nos ajuda a lembrar o que nosso circuito deve fazer nessa condição.

• O primeiro círculo é a condição “stand-by”. É aqui que o nosso circuito começa e onde aguarda que outro botão seja pressionado.
• O segundo círculo é a condição em que o botão acabou de ser pressionado e nosso circuito precisa transmitir um pulso ALTO.
• O terceiro círculo é a condição em que nosso circuito espera que o botão seja liberado antes de retornar à condição “stand-by”.

Na parte inferior do círculo está a saída do nosso circuito. Se quisermos que nosso circuito transmita um HIGH em um estado específico, colocamos 1 nesse estado. Caso contrário, colocamos um 0.

Cada seta representa uma “transição” de um estado para outro. Uma transição acontece uma vez a cada ciclo de clock. Dependendo da entrada atual, podemos ir para um estado diferente a cada vez. Observe o número no meio de cada seta. Esta é a entrada atual.

Por exemplo, quando estamos no estado “Em espera inicial” e “lemos” um 1, o diagrama nos diz que devemos ir para o estado “Ativar pulso”. Se lermos 0, devemos permanecer no estado “Em espera inicial”.

Então, o que nossa “Máquina” faz exatamente? Ele começa no estado “Inicial - Em espera” e espera até que 1 seja lido na entrada. Em seguida, ele vai para o estado “Ativar pulso” e transmite um pulso HIGH em sua saída. Se o botão continuar pressionado, o circuito vai para o terceiro estado, o “Wait Loop”.

Lá, ele espera até que o botão seja liberado (a entrada vai para 0) enquanto transmite um LOW na saída. Então está tudo de novo!

Esta é possivelmente a parte mais difícil do procedimento de design, porque não pode ser descrita por etapas simples. É preciso experiência e um pouco de raciocínio aguçado para configurar um Diagrama de Estados, mas o resto é apenas um conjunto de etapas predeterminadas.

Etapa 3

Em seguida, substituímos as palavras que descrevem os diferentes estados do diagrama por binário números. Começamos a enumeração de 0, que é atribuído no estado inicial. Em seguida, continuamos a enumeração com qualquer estado que quisermos, até que todos os estados tenham seus números. O resultado é mais ou menos assim:(Figura abaixo)

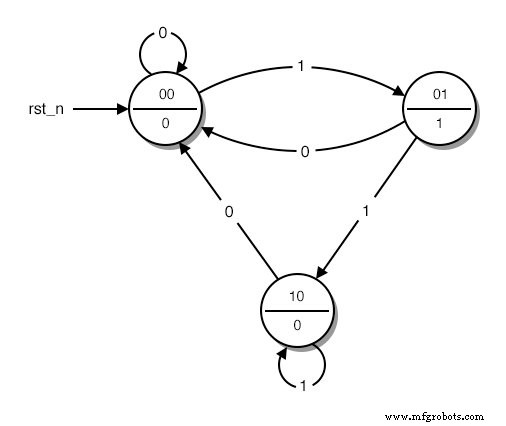
Um diagrama de estado com estados codificados

Etapa 4

Depois, preenchemos a Tabela de estado . Essa tabela tem um formato bem específico. Vou dar a tabela do nosso exemplo e usá-la para explicar como preenchê-la. (Figura abaixo)

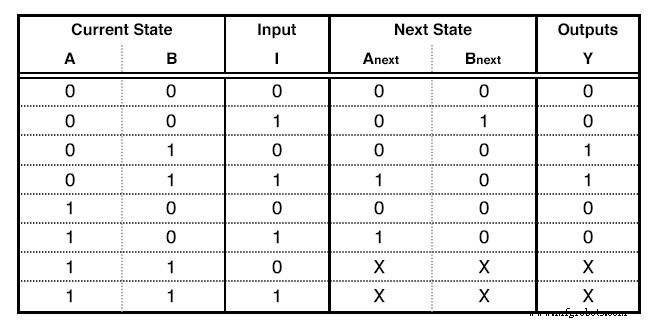
Uma tabela de estado

As primeiras colunas são tantos quanto os bits do número mais alto que atribuímos ao Diagrama de Estado. Se tivéssemos 5 estados, teríamos usado até o número 100, o que significa que usaríamos 3 colunas. Para nosso exemplo, usamos até o número 10, portanto, apenas 2 colunas serão necessárias. Estas colunas descrevem o Estado Atual do nosso circuito.

À direita das colunas do estado atual, escrevemos as Colunas de entrada . Elas serão tantas quanto nossas variáveis ​​de entrada. Nosso exemplo possui apenas uma entrada.

Em seguida, escrevemos as Colunas do próximo estado . São tantos quanto as colunas Estado Atual.

Finalmente, escrevemos as Colunas de Saídas . Estes são tantos quanto nossos resultados. Nosso exemplo tem apenas uma saída. Como construímos uma Máquina de Estados Mais Finitos, a saída depende apenas dos estados de entrada atuais. Esta é a razão pela qual a coluna de saídas tem dois 1:para resultar em uma função booleana de saída que é independente da entrada I. Continue lendo para mais detalhes. As colunas Estado Atual e Entrada são as Entradas de nossa tabela. Nós os preenchemos com todos os números binários de 0 a:

2 ^{(número de colunas do estado atual + número de colunas de entrada)} -1

É mais simples do que parece felizmente. Normalmente, haverá mais linhas do que os estados reais que criamos no Diagrama de estado, mas tudo bem.

Cada linha das colunas do próximo estado é preenchida da seguinte forma:Nós a preenchemos com o estado que alcançamos quando, no Diagrama de estados, do estado atual da mesma linha seguimos a entrada da mesma linha. Se tiver que preencher uma linha cujo número de estado atual não corresponda a nenhum estado real no Diagrama de estado, nós o preencheremos com os termos Não me importo (X). Afinal, não nos importamos para onde podemos ir de um estado que não existe. Em primeiro lugar, não estaríamos lá! Novamente, é mais simples do que parece.

A coluna de saídas é preenchida pela saída do estado atual correspondente no diagrama de estados.

A Tabela de estado está completa! Ele descreve o comportamento de nosso circuito de forma tão completa quanto o diagrama de estados.

Etapa 5a

O próximo passo é pegar essa “Máquina” teórica e implementá-la em um circuito. Na maioria das vezes, essa implementação envolve flip-flops. Este guia é dedicado a este tipo de implementação e irá descrever o procedimento tanto para D - Flip Flops quanto JK - Flip Flops. T - Flip-flops não serão incluídos porque são muito semelhantes aos dois casos anteriores. A seleção do flip-flop a ser usado é arbitrária e geralmente é determinada por fatores de custo. A melhor escolha é realizar a análise e decidir qual tipo de Flip Flop resulta em um número mínimo de portas lógicas e menor custo.

Primeiro, examinaremos como implementamos nossa “Máquina” com D-flip-flops.

Precisaremos de tantos D-flip-flops quantas colunas de estado, 2 em nosso exemplo. Para cada flip-flop, adicionaremos mais uma coluna em nossa tabela de estados (Figura abaixo) com o nome da entrada do flip-flop, “D” para este caso. A coluna que corresponde a cada flip-flop descreve que entrada devemos dar ao flip-flop para ir do estado atual para o próximo estado . Para o D-Flip Flop, isso é fácil:a entrada necessária é igual ao próximo estado. Nas linhas que contêm Xs, também preenchemos Xs nesta coluna.

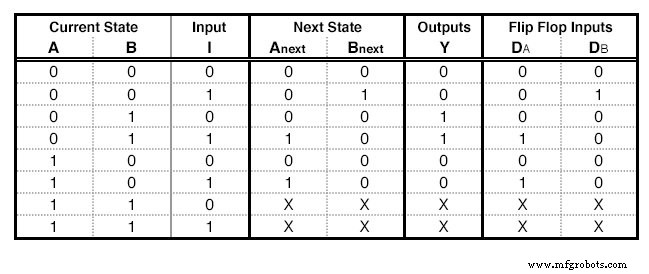
Uma tabela de estado com D - Excitações de flip-flop

Etapa 5b

Podemos fazer os mesmos passos com JK - Flip Flops. No entanto, existem algumas diferenças. Um JK - Flip Flop possui duas entradas, portanto, precisamos adicionar duas colunas para cada Flip Flop. O conteúdo de cada célula é ditado pela tabela de excitação de JK:



Esta tabela diz que se quisermos ir do Estado Q para o Estado Q _próximo , precisamos usar a entrada específica para cada terminal. Por exemplo, para ir de 0 a 1, precisamos alimentar J com 1 e não nos importamos qual entrada alimentamos ao terminal K.

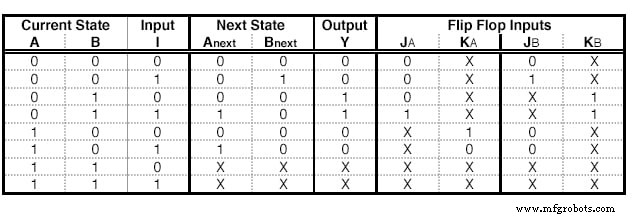
Uma tabela de estado com JK - excitações de flip-flop



Etapa 6

Estamos na fase final do nosso procedimento. O que resta é determinar as funções booleanas que produzem as entradas de nossos flip-flops e a saída. Extrairemos uma função booleana para cada entrada do Flip Flop que tivermos. Isso pode ser feito com um mapa de Karnaugh. As variáveis ​​de entrada deste mapa são as variáveis ​​do estado atual e também as entradas.

Dito isso, as funções de entrada para nossos D - Flip Flops são as seguintes:(Figura abaixo)

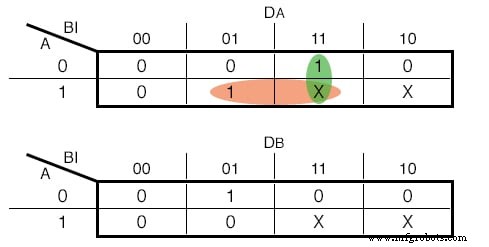
Mapas de Karnaugh para D - entradas de flip-flop



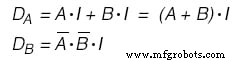
Se optássemos por usar JK - Flip Flops nossas funções seriam as seguintes:(Figura abaixo)

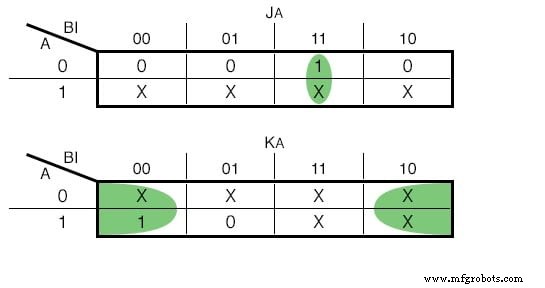
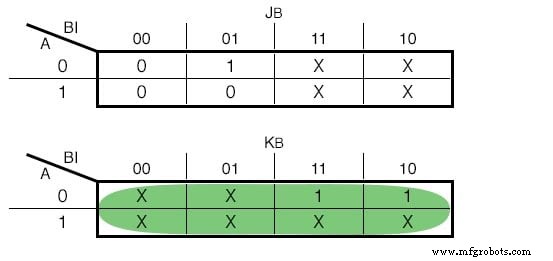
Mapa de Karnaugh para o JK - Entrada Flip Flop



Um mapa de Karnaugh também será usado para determinar a função da saída:(Figura abaixo)

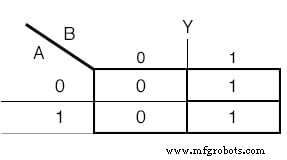
Mapa de Karnaugh para a variável de saída Y



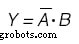
Etapa 7

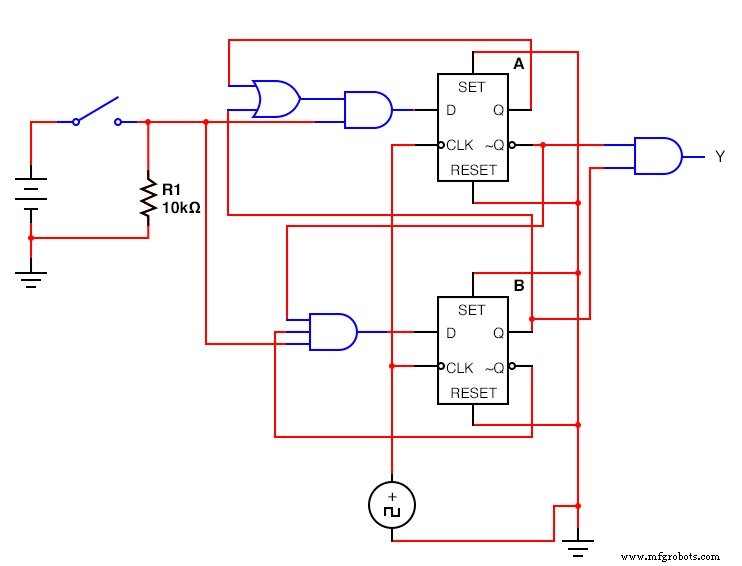
Nós projetamos nosso circuito. Colocamos os flip-flops e usamos portas lógicas para formar as funções booleanas que calculamos. As portas recebem dados da saída dos flip-flops e da entrada do circuito. Não se esqueça de conectar o relógio aos flip-flops!

A versão D - Flip Flop:(Figura abaixo)

O D - Circuito Sequencial Flip Flop concluído



A versão JK - Flip Flop:(Figura abaixo)

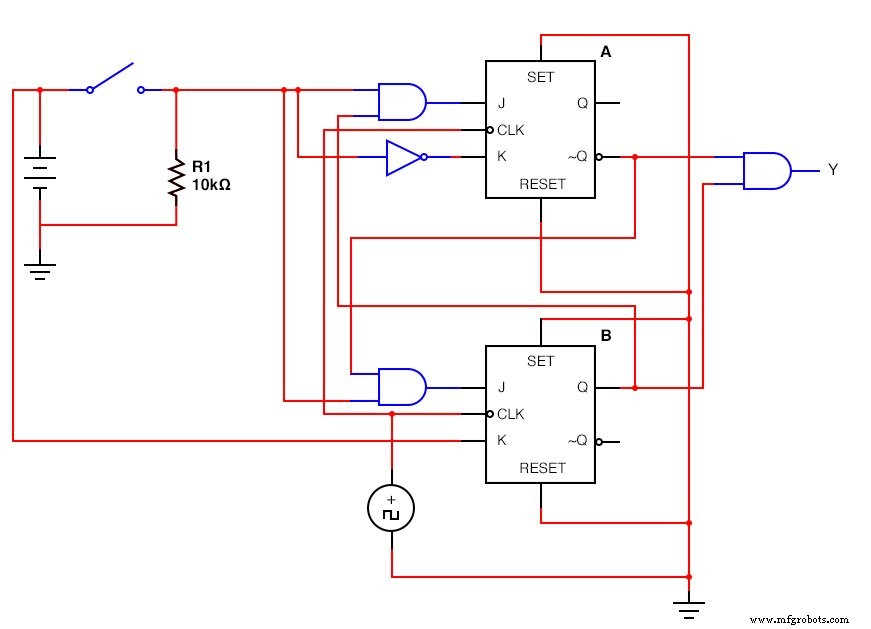
O JK - Circuito Sequencial Flip Flop concluído



É isso! Projetamos e construímos com sucesso um circuito sequencial. A princípio pode parecer uma tarefa difícil, mas depois de prática e repetição, o procedimento se tornará trivial. Os circuitos sequenciais podem ser úteis como partes de controle de circuitos maiores e podem executar qualquer tarefa lógica sequencial que possamos imaginar. O céu é o limite! (ou a placa de circuito, pelo menos)

REVER:

• Uma função de lógica sequencial tem um recurso de “memória” e leva em consideração entradas anteriores para decidir sobre a saída.
• A máquina de estados finitos é um modelo matemático abstrato de uma função lógica sequencial. Possui entradas, saídas e número de estados finitos.
• FSMs são implementados em circuitos da vida real por meio do uso de flip-flops
• O procedimento de implementação precisa de uma ordem específica de etapas (algoritmo) para ser executado.