Teorema de Norton. Procedimento passo a passo fácil com exemplo

Teorema de Norton na análise de circuitos CC

O teorema de Norton é outra técnica útil para analisar circuitos elétricos, como usar o Teorema de Thevenin, que reduz circuitos lineares ativos e redes complexas em um circuito equivalente simples. A principal diferença entre o teorema de Thevenin e o teorema de Norton é que, o teorema de Thevenin fornece uma fonte de tensão equivalente e uma resistência em série equivalente, enquanto o teorema de Norton fornece uma fonte de corrente equivalente e uma resistência paralela equivalente.

Teorema de Norton afirma que:

Em outras palavras, qualquer circuito linear é equivalente a uma fonte de corrente real e independente em terminais específicos.

Post relacionado:Teorema de Thévenin. Procedimento passo a passo fácil com exemplo (visualizações pictóricas)

Etapas para analisar um circuito elétrico usando o teorema de Norton

1. Encurte o resistor de carga.
2. Calcule/meça a Corrente de Curto-Circuito. Esta é a corrente de Norton (I_N ).
3. Fontes de Corrente Aberta, Fontes de Curta Tensão e Resistor de Carga Aberta.
4. Calcule/meça a resistência de circuito aberto. Esta é a resistência do Norton (R_N ).
5. Agora, redesenhe o circuito com corrente de curto-circuito medida (I_N ) na Etapa (2) como Fonte de Corrente e resistência de circuito aberto medida (R_N ) na etapa (4) como uma resistência paralela e conecte o resistor de carga que removemos na etapa (3). Este é o Circuito Norton Equivalente daquela Rede Elétrica Linear ou Circuito Complexo que teve que ser simplificado e analisado. Você fez isso.
6. Agora, encontre a corrente de carga que flui e a tensão de carga no resistor de carga usando a regra do divisor de corrente. Eu_E =I_N / (R_N / (R_N + R_L ))  ((Para uma explicação clara... verifique o exemplo resolvido abaixo).

Exemplo resolvido por Norton Teorema:

Exemplo:

Encontre R_N , I_N , a corrente que flui através e a tensão de carga através do resistor de carga na fig (1) usando o Teorema de Norton.

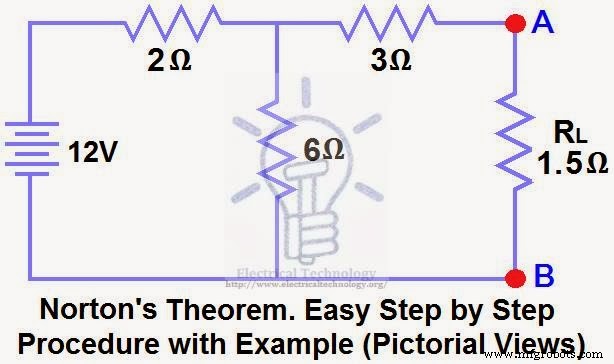
  Solução:-

ETAPA 1.

Encurte o resistor de carga de 1,5Ω como mostrado na (Fig 2).

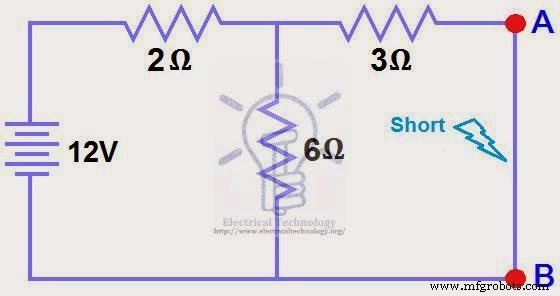
ETAPA 2.

Calcule/meça a Corrente de Curto-Circuito. Esta é a corrente de Norton (I_N ).

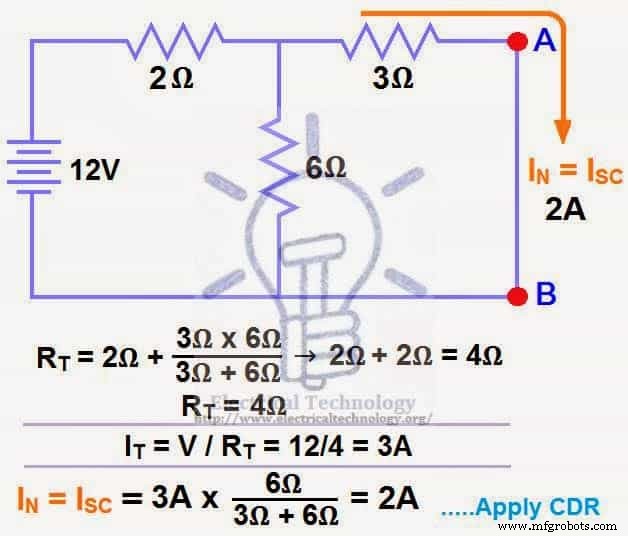
Nós encurtamos os terminais AB para determinar a corrente do Norton, I_N. Os 6Ω e 3Ω estão então em paralelo e esta combinação paralela de 6Ω e 3Ω estão então em série com 2Ω.

Então a resistência total do circuito para a Fonte é:-

2Ω + (6Ω || 3Ω) ….. (|| =em paralelo com).

R_T =2Ω + [(3Ω x 6Ω) / (3Ω + 6Ω)] → I_T =2Ω + 2Ω =4Ω.

R_T =4Ω

Eu_T =V ÷ R_T

Eu_T =12V ÷ 4Ω

Eu_T =3A..

Agora temos que encontrar I_SC =I_N   … Aplicar CDR… (Regra do Divisor Atual)…

Eu_SC =I_N =3A x [(6Ω ÷ (3Ω + 6Ω)] =2A.

Eu_SC =I_N =2A.

ETAPA 3.

Fontes de Corrente Abertas, Fontes de Curta Tensão e Resistor de Carga Aberta. Figura (4)

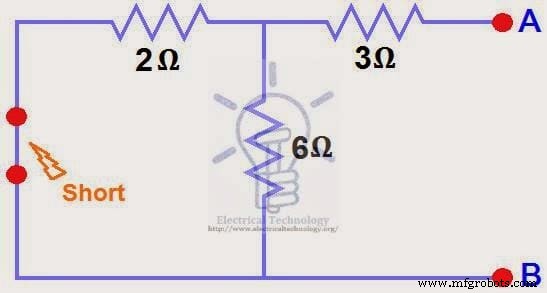
ETAPA 4.

Calcule/meça a Resistência de Circuito Aberto. Esta é a resistência do Norton (R_N )

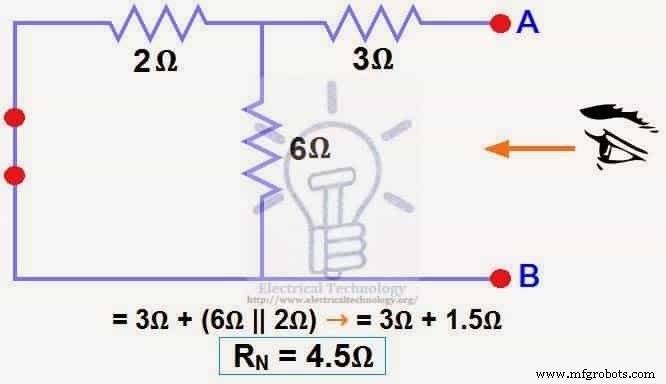
Reduzimos a fonte de 12V DC para zero é equivalente a substituí-la por um curto na etapa (3), conforme mostrado na figura (4)  Podemos ver que o resistor de 3Ω é em série com uma combinação paralela de resistor de 6Ω e resistor de 2Ω. ou seja:

3Ω + (6Ω || 2Ω) ….. (|| =em paralelo com)

R_N =3Ω + [(6Ω x 2Ω) ÷ (6Ω + 2Ω)]

R_N =3Ω + 1,5Ω

R_N =4,5Ω



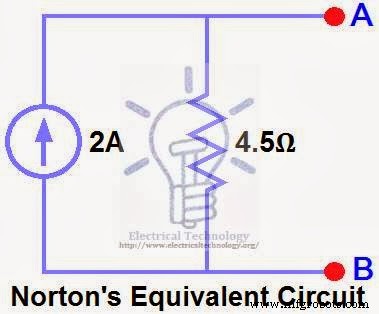
ETAPA 5.

Conecte o R_N em paralelo com a fonte atual I_N  e reconecte o resistor de carga. Isso é mostrado na fig (6), ou seja, circuito equivalente de Norton com resistor de carga.

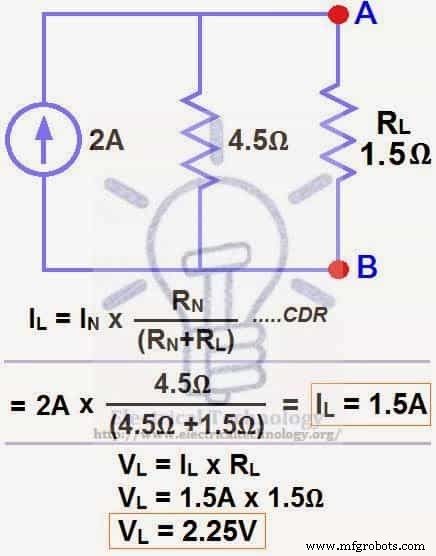
ETAPA 6.

Agora aplique a última etapa, ou seja, calcule a corrente de carga e a tensão de carga no resistor de carga pela Lei de Ohm, conforme mostrado na fig 7.

Carregar corrente através do resistor de carga…

E_L =I_N x [R_N ÷ (R_N + R_L )]

=2A x (4,5Ω ÷ 4,5Ω + 1,5Ω) → =1,5A

I_L =1. 5A

E

Tensão de carga no resistor de carga…

V_L =E_E x R_L

V_L =1,5A x 1,5Ω

V_L =2,25V

Agora compare este circuito simples com o circuito original fornecido na figura 1. Você pode ver como será mais fácil medir/calcular a corrente de carga e a tensão de carga para diferentes resistores de carga através do Teorema de Norton mesmo em circuitos muito mais complexos? Somente e somente sim.

É bom saber: Os teoremas de Norton e Thevenin podem ser aplicados a circuitos CA e CC contendo componentes de diferença, como resistores, indutores e capacitores, etc. Lembre-se de que a corrente do Norton "I_N ” no circuito AC é expresso em número complexo (forma polar), enquanto a resistência de Norton “R_N ” é indicado em forma retangular.

Postagens relacionadas:

• Teorema de transferência de potência máxima para circuitos CA e CC
• Lei de Corrente e Tensão de Kirchhoff (KCL e KVL) | Exemplo resolvido
• Teorema da Compensação - Demonstração, Explicação e Exemplos Resolvidos
• Teorema da Substituição – Guia Passo a Passo com Exemplo Resolvido
• Teorema de Millman – Análise de circuitos CA e CC – Exemplos
• Teorema da Superposição - Análise de Circuito com Exemplo Resolvido
• Teorema de Tellegen - Exemplos Resolvidos e Simulação MATLAB
• Análise de circuitos SUPERNODE | Passo a passo com exemplo resolvido
• SUPERMESH Análise de Circuitos | Passo a passo com exemplo resolvido
• Regra do divisor de tensão (VDR) - Exemplos resolvidos para circuitos R, L e C
• Regra do divisor de corrente (CDR) – Exemplos resolvidos para circuitos CA e CC
• Conversão de Estrela para Delta e Delta para Estrela. Transformação Y-Δ