Ressonâncias Fano de banda dupla de fator de alta qualidade induzidas por estados de ligação dupla no continuum usando uma laje de nanofuro planar
Resumo
Na fotônica, é essencial alcançar ressonâncias de fator (Q) de alta qualidade para melhorar o desempenho dos dispositivos ópticos. Aqui, demonstramos que as ressonâncias Fano de banda dupla de fator Q alto podem ser alcançadas usando uma placa de nanohole planar (PNS) com base na excitação de estados de ligação dupla no continuum (BICs). Ao encolher ou expandir os orifícios tetramerizados da superrede do PNS, dois BICs protegidos por simetria podem ser induzidos a ressonâncias Fano de banda dupla e suas localizações, bem como seus fatores Q podem ser ajustados de forma flexível. Os mecanismos físicos para as ressonâncias Fano de banda dupla podem ser interpretados como os acoplamentos ressonantes entre os dipolos toroidais elétricos ou os dipolos toroidais magnéticos com base nas decomposições múltiplas de campo distante e nas distribuições de campo próximo da superrede. As ressonâncias Fano de banda dupla do PNS possuem característica independente de polarização e podem sobreviver mesmo quando os parâmetros geométricos do PNS são significativamente alterados, tornando-os mais adequados para aplicações potenciais.
Introdução
O aumento da interação entre luz e matéria, o que é significativo para melhorar o desempenho de dispositivos ópticos, pode ser realizado usando respostas de fator (Q) de alta qualidade [1]. A ressonância de Fano, caracterizada pela forma de linha assimétrica e perfil espectral nítido, fornece uma abordagem eficaz para atingir o alto fator Q em metamateriais ópticos e tem recebido grande atenção [2]. Na última década, a ressonância Fano foi relatada em muitos sistemas osciladores em nanoescala habilitados por nanoestruturas plasmônicas [3, 4], onde a ressonância Fano é excitada pela ressonância do plasma de superfície na interface metal-dielétrica. Embora os metamateriais metálicos sejam candidatos promissores para manipulação de luz, a ressonância Fano em metamateriais plasmônicos normalmente sofre de fator Q baixo nas regiões espectrais do visível ao infravermelho próximo (NIR) devido às perdas óhmicas inerentes no metal.
Por outro lado, os metamateriais totalmente dielétricos fornecem fortes ressonâncias do tipo Mie com correntes de deslocamento induzidas semelhantes às dos metamateriais plasmônicos, mas apresentam menos perdas dissipativas na faixa do visível ao NIR [5]. A energia da luz incidente pode ser altamente localizada nas nanoestruturas dielétricas devido à excitação das ressonâncias dipolares elétricas e / ou magnéticas, o que reduz as perdas dissipativas e atinge grande aumento ressonante de campos elétricos e magnéticos. Nos últimos anos, os estados ligados no continuum (BICs) surgiram como o esquema mais promissor para alcançar respostas de fator Q alto em metamateriais totalmente dielétricos [6, 7]. BICs residem dentro do espectro contínuo de estados estendidos, mas contra-intuitivamente permanecem perfeitamente localizados no espaço com vida teoricamente infinita [8, 9]. Embora os BICs não sejam observáveis a partir do espectro contínuo devido à propriedade não radiativa, as ressonâncias de Fano com alto fator Q podem ser alcançadas conforme os BICs são transformados em quase-BICs (QBICs) [10, 11], as aplicações potenciais incluem, como direcional lasing [12], filtros ópticos [13], conversão de frequência não linear [14], sensores ultra-sensíveis [15, 16] e feixes de vórtices ópticos [17].
Geralmente, a formação de BICs está fortemente relacionada às simetrias (no plano e simetria vertical) da estrutura fotônica devido à sua natureza interferencial. Mais especialmente, os BICs podem ser perturbados por meio de incidência oblíqua ou nanoestruturas com quebra de simetria, e os QBICs podem ser realizados quando o canal de radiação entre os estados próprios e o espaço livre é aberto [18, 19]. No entanto, a maioria das nanoestruturas dielétricas usadas para excitar QBICs com alto fator Q são complicadas, como nanocrosses assimétricos [20], nanorings assimétricos [21], nanobares assimétricos [22,23,24] e nanobastões assimétricos [25,26, 27,28], que são desafiadores na fabricação devido à necessidade de inserir as fendas profundas do comprimento de onda [20,21,22,23,24] ou nanoholes [25,26,27,28] nas estruturas fotônicas. Outras nanoestruturas, como as barras retangulares remodeladas [29, 30], têm bordas afiadas aumentadas, tornando-as mais difíceis de serem fabricadas com precisão por meio de técnicas litográficas convencionais, o que reduz o fator Q e a vida de ressonância dos dispositivos devido à abertura de canais com vazamento adicionais [31, 32]. Além disso, os nanobares inclinados [33, 34], outro tipo de estrutura, apresentam dificuldades no controle preciso da orientação dos nanobares com os espaços de comprimento de onda profundo entre os ressonadores mantidos no processo de nanofabricação. Em aplicações, é significativo realizar BICs e ressonâncias Fano de alto fator Q usando metamateriais totalmente dielétricos com arquiteturas mais simples, como as lajes planas nanoestruturadas [35,36,37,38]. Além disso, múltiplas ressonâncias Fano são muito úteis em aplicações como aumento da geração de harmônicos multibanda [39], sensoriamento multicanal [40] e emissão de luz [41]. Portanto, há um benefício significativo para alcançar múltiplas ressonâncias Fano de alto fator Q usando uma arquitetura comparativamente simples baseada na excitação de QBICs.
Neste trabalho, uma nova placa de nanohole planar (PNS) consistindo de furos tetramerizados é proposta para alcançar ressonâncias Fano de banda dupla de fator Q alto. Ao reduzir ou expandir os orifícios tetramerizados do PNS ao longo das diagonais da superrede, dois QBICs são excitados e as localizações das duas ressonâncias de Fano, bem como seus fatores Q, podem ser ajustados de forma flexível. Decomposições múltiplas de campo distante e distribuições de campo próximo da superrede são realizadas para revelar as características ressonantes do PNS, indicando que as ressonâncias Fano de banda dupla são resultantes dos acoplamentos ressonantes entre os dipolos toroidais elétricos ou os dipolos toroidais magnéticos. As ressonâncias Fano de banda dupla do PNS possuem característica independente de polarização, e podem sobreviver até mesmo os parâmetros geométricos do PNS são significativamente alterados, tornando-o mais adequado para aplicações potenciais.
Métodos
Estrutura e design da rede
A Figura 1 mostra a geometria esquemática do PNS proposto e seus espectros de transmissão. O PNS consiste em quatro nanofuros que podem ser encolhidos (Δ <0) ou expandidos (Δ> 0) com uma distância de deslocamento de Δ ao longo das diagonais da superrede, e Δ =0 corresponde a uma rede simples com período reduzido à metade, onde cada nanofuro está localizado no centro de um quarto da área da superrede. O período e a altura do PNS são Λ e H, respectivamente; o raio do nanofuro é r . O índice de refração do PNS é n s =3.2, e o fundo é ar com o índice de refração de n a =1. A Figura 1c mostra os espectros do PNS como uma função da distância de deslocamento de Δ, onde o PNS é iluminado por um incidente normal x -luz polarizada. Os espectros, bem como as distribuições do campo eletromagnético do PNS apresentadas neste artigo, são calculados usando o software comercial do método dos elementos finitos da COMSOL Multiphysics. Conforme mostrado na Fig. 1c, não há ressonância Fano para o PNS não encolhido com Δ =0. No entanto, duas ressonâncias Fano com profundidades de modulação de 100% (definidas como as diferenças de transmissão entre picos Fano e depressões Fano) podem ser obtidas por encolhendo ligeiramente ou expandindo os nanoholes. Comparando com a resposta de transmissão do PNS não encolhido, a resposta de transmissão do PNS encolhido varia abruptamente enquanto as bandas laterais são mantidas quase as mesmas.
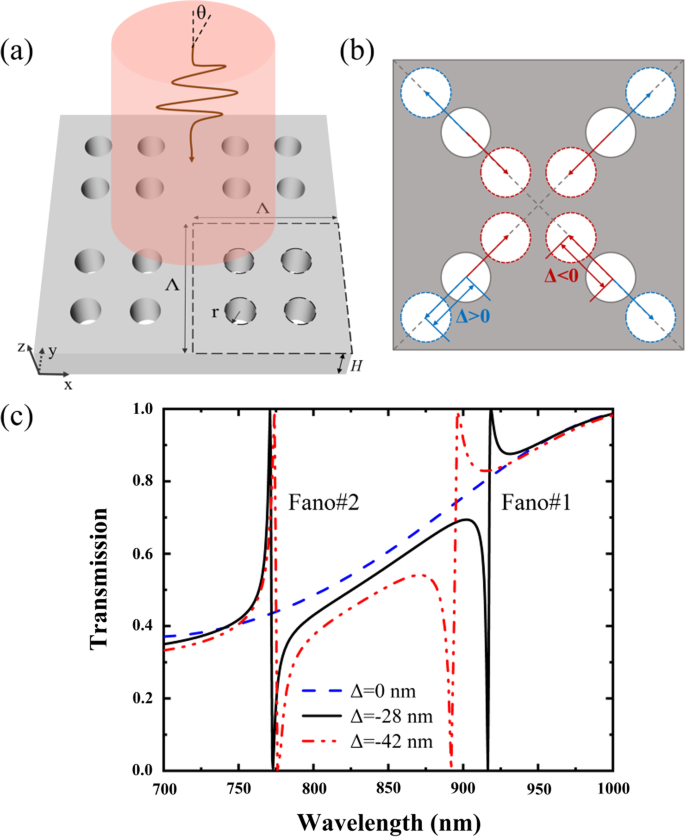
a Vista em perspectiva do PNS. b Visão vertical do PNS como quatro nanofuros encolhem (Δ <0) ou expandem (Δ> 0) ao longo das diagonais da superrede. c Espectros de transmissão do PNS em função da distância de deslocamento de Δ. O PNS está sob a iluminação do x - onda incidente polarizada com o ângulo de incidência de θ =0. Os parâmetros do PNS são:Λ =350 nm, r =35 nm e H =175 nm
Para mostrar claramente a evolução das ressonâncias Fano de banda dupla decorrentes do encolhimento ou expansão dos orifícios tetramerizados, o mapa 2D de transmissão do PNS como uma função da distância de deslocamento de Δ é mostrado na Fig. 2a. Conforme mostrado na Fig. 2a, dois BICs ocorrem na região de comprimento de onda de interesse como Δ =0, e fenômeno semelhante de BICs duplos foi relatado anteriormente nas estruturas de metamembranas de grade dupla [13] e ressonador de anel dividido [21]. No caso de Δ ≠ 0, ressonâncias Fano de banda dupla são realizadas como BICs são induzidos a QBICs devido à quebra de simetria do PNS, ou seja, da centrossimetria da rede simples para a rotacional quádrupla (C 4 ) simetria da superrede. Além disso, porque o C 4 a simetria do PNS pode ser mantida conforme os orifícios tetramerizados são encolhidos ou expandidos ao longo das diagonais da superrede, os espectros de transmissão do PNS são os mesmos para o mesmo valor absoluto de | Δ |. Em princípio, o encolhimento ou expansão dos orifícios tetramerizados reduz a área da primeira zona de Brillouin do PNS conforme a célula unitária do PNS muda de rede simples para superrede, e BIC protegido por simetria pode ser excitado na incidência normal devido ao introdução de perturbação de superfície, bem como dobramento da zona de Brillouin do PNS [42, 43]. Geralmente, o fator Q de um BIC protegido por simetria mostra uma dependência quadrada inversa no grau de assimetria δ com base na teoria de perturbação [21]:
$$ Q_ {fit} =\ kappa \ cdot \ frac {cS} {{\ omega \ cdot \ delta ^ {2}}}, $$ (1)
onde ĸ é uma constante de proporcionalidade, S é a área de uma superrede, ω é a frequência angular e o parâmetro de assimetria é \ (\ delta {=} \ sqrt 2 \ Delta / \ Lambda \).
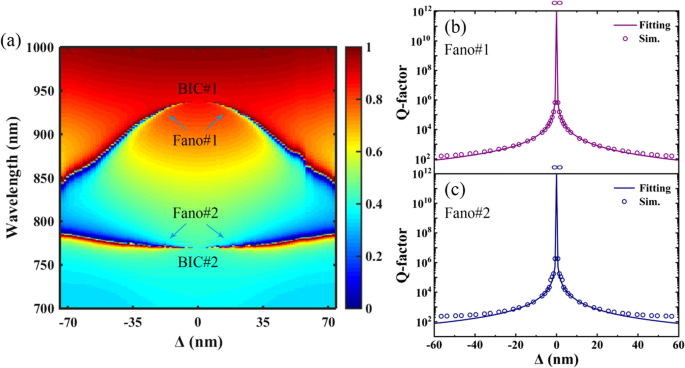
a Mapa 2D de transmissão do PNS em função da distância de deslocamento de Δ ao longo das diagonais da superrede. b e c Fator Q e o resultado de ajuste de Fano # 1 e Fano # 2, respectivamente. Outros parâmetros são iguais aos da Fig. 1c
A Figura 2b, c mostra o fator Q e o resultado do ajuste de Fano # 1 e Fano # 2, respectivamente. O fator Q do PNS é calculado como uma razão entre o comprimento de onda de ressonância λ r e sua largura total na metade do máximo (FWHM) Δλ, onde Δλ é a região do comprimento de onda entre o pico e o mergulho da ressonância de Fano. Os resultados de ajuste do PNS são calculados usando a Eq. (1). Como mostrado na Fig. 2b, c, trajetórias divergentes do PNS onde os fatores Q divergem para o infinito em Δ =0 são validadas usando a relação quadrada inversa para ajustar os dados. Excelentes resultados de ajuste podem ser obtidos e a ligeira discordância na assimetria maior é devido ao desvio da suposição de pequena perturbação na Eq. (1). A vantagem significativa do PNS é que a localização e o fator Q das ressonâncias Fano de banda dupla podem ser ajustados reduzindo ou expandindo os orifícios tetramerizados, o que facilita o controle dinâmico dos desempenhos ressonantes do múltiplo de alto fator Q Ressonâncias de Fano.
Mecanismos físicos e interpretação
Para obter um insight sobre a origem das ressonâncias Fano de banda dupla por meio da redução ou expansão dos orifícios tetramerizados do PNS, decompomos a radiação de campo distante da ressonância BIC e Fano em contribuições de diferentes componentes multipolares para discutir melhor suas características. Os momentos multipolares podem ser calculados com base na densidade de corrente de deslocamento j na superrede do PNS [26, 44, 45]:
$$ {\ varvec {P}} =\ frac {1} {i \ omega} \ int {{\ varvec {j}} d ^ {3} r}, $$ (2) $$ {\ varvec {M }} =\ frac {1} {2c} \ int {\ left ({{\ varvec {r}} \ times {\ varvec {j}}} \ right) d ^ {3} r}, $$ (3 ) $$ {\ varvec {T}} =\ frac {1} {10c} \ int {\ left [{\ left ({{\ varvec {r}} \ cdot {\ varvec {j}}} \ right) {\ varvec {r}} - 2r ^ {2} {\ varvec {j}}} \ right]} d ^ {3} r, $$ (4) $$ {\ varvec {Q}} _ {\ alpha , \ beta} ^ {\ left (e \ right)} =\ frac {1} {i2 \ omega} \ int {\ left [{r _ {\ alpha} j _ {\ beta} + r _ {\ beta} j_ { \ alpha} - \ frac {2} {3} \ left ({{\ varvec {r}} \ cdot {\ varvec {j}}} \ right)} \ delta _ {\ alpha, \ beta} \ right] } d ^ {3} r $$ (5) $$ {\ varvec {Q}} _ {\ alpha, \ beta} ^ {\ left (m \ right)} =\ frac {1} {3c} \ int {\ left [{\ left ({{\ varvec {r}} \ times {\ varvec {j}}} \ right) _ {\ alpha} r _ {\ beta} + \ left ({{\ varvec {r} } \ times {\ varvec {j}}} \ right) _ {\ beta} r _ {\ alpha}} \ right] d ^ {3} r}, $$ (6)
onde P , M , T , Q ( e ) e Q ( m ) são os momentos de dipolo elétrico (ED), dipolo magnético (MD), dipolo toroidal (TD), quadrupolo elétrico (EQ) e quadrupolo magnético (MQ), respectivamente; c é a velocidade da luz no vácuo, e α , β = x , y , z . Aqui, a densidade de carga ρ , que geralmente aparece na definição de ED e MQ, foi substituído por densidade de corrente de deslocamento j via relação de conservação de carga de \ (i \ omega \ rho + \ nabla \ cdot {\ varvec {j}} =0 \). No caso de excitação harmônica ~ exp ( iωt ), o poder de espalhamento dos momentos multipolares induzidos que contribuem para a resposta de campo distante pode ser escrito como:
$$ \ begin {align} I &=\ frac {{2 \ omega ^ {4}}} {{3c ^ {3}}} \ left | {\ varvec {P}} \ right | ^ {2} + \ frac {{2 \ omega ^ {4}}} {{3c ^ {3}}} \ left | {\ varvec {M}} \ right | ^ {2} + \ frac {{2 \ omega ^ {6}}} {{3c ^ {5}}} \ left | {\ varvec {T}} \ right | ^ {2} + \ frac {{\ omega ^ {6}}} {{5c ^ {5}}} \ sum \ limits _ {\ alpha, \ beta} {\ left | {{\ varvec {Q}} _ {\ alpha, \ beta} ^ {\ left (e \ right)}} \ right |} ^ {2} \\ &\ quad + \ frac {{\ omega ^ {6} }} {{20c ^ {5}}} \ sum \ limits _ {\ alpha, \ beta} {\ left | {{\ varvec {Q}} _ {\ alpha, \ beta} ^ {\ left (m \ right)}} \ right |} ^ {2} + {\ text {o}} (\ omega), \ end {alinhado} $$ (7)
onde os primeiros dois termos correspondem ao ED convencional (carga) e espalhamento MD. O terceiro termo corresponde ao espalhamento TD. O quarto e o quinto termos vêm de EQ e MQ. O último termo é o termo de ordem superior que contém o espalhamento multipolar de alta ordem e o acoplamento entre eles e pode ser geralmente ignorado. Usando as Eqs. (2) - (7), as contribuições de diferentes multipolos para o poder de espalhamento do campo distante podem ser obtidas.
A Figura 3 mostra o poder de espalhamento de diferentes multipolares do PNS para diferentes distâncias de deslocamento de Δ, outros parâmetros são os mesmos da Fig. 1c. Conforme mostrado na Fig. 3a-d, para o PNS com Δ =0, ED e MD são os dipolos dominantes e não são ressonantes na região do comprimento de onda de interesse. No entanto, ao encolher ou expandir os nanoholes do PNS com | Δ | ≠ 0, ressonâncias Fano de banda dupla podem ser realizadas devido às excitações dos modos de dipolo ressonante. Para ver claramente os papéis importantes dos modos de dipolo ressonante na formação das ressonâncias Fano de banda dupla observadas, Fig. 3e, f mostra o poder de espalhamento normalizado de diferentes multipolos com Δ =- 28 nm em torno de Fano # 1 e Fano # 2, respectivamente . Como mostrado na Fig. 3e, os modos ressonantes dominantes são ED e TD em torno de Fano # 1, e Fano # 1 é a consequência direta do acoplamento ressonante dos dipolos toroidais elétricos. Em particular, ED e TD são fortemente aumentados para uma magnitude comparável na ponta ressonante (918,5 nm) de Fano # 1; assim, 100% de transmissão pode ser obtida devido à interferência destrutiva entre ED e TD. Já para o mergulho ressonante (916,5 nm) de Fano # 1, a reflexão é maximizada e a transmissão vai para zero devido ao espalhamento aprimorado de ED e TD. Da mesma forma, como mostrado na Fig. 3f, Fano # 2 está surgindo do acoplamento ressonante dos dipolos toroidais magnéticos, sua ponta (771,1 nm) indica a interferência destrutiva entre MD e TD, enquanto seu mergulho (772,9 nm) está associado ao espalhamento aprimorado de MD e TD. Observe que, devido ao forte acoplamento de dipolos toroidais elétricos ou dipolos toroidais magnéticos, os modos ressonantes são robustos para Fano # 1 e Fano # 2, mesmo se Δ for variado.
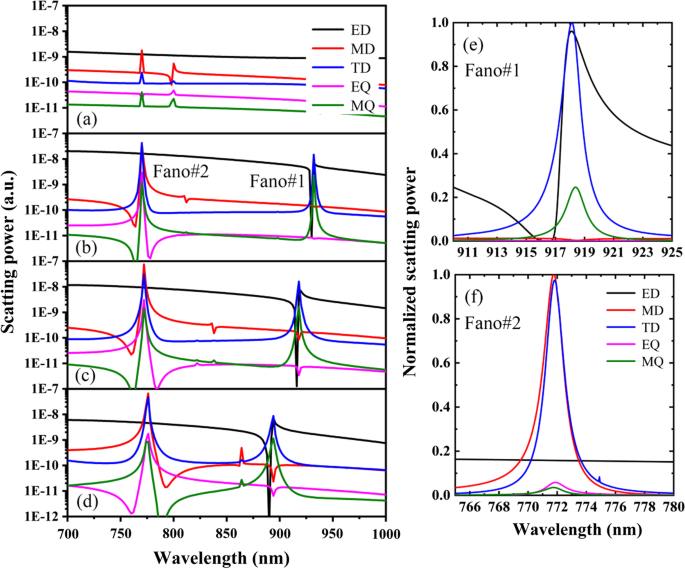
Poder de dispersão do ED cartesiano, MD, TD, EQ e MQ quando a Δ =0, b Δ =- 14 nm, c Δ =- 28 nm e d Δ =- 42 nm. e e f Poder de espalhamento normalizado de diferentes multipolares com Δ =- 28 nm em torno de Fano # 1 e Fano # 2, respectivamente. Outros parâmetros são iguais aos da Fig. 1c
Para vincular a resposta de transmissão de ressonâncias Fano de banda dupla no campo distante com as excitações de momentos multipolares induzidos, as distribuições de campo eletromagnético e corrente de deslocamento de ressonâncias de Fano da superrede do PNS são mostradas na Fig. 4. Como mostrado em Fig. 4a, b, o campo elétrico de Fano # 1 está bem confinado na superrede do PNS com a corrente de deslocamento ao longo do x eixo, indicando um modo ressonante ED. Além disso, a corrente de deslocamento do Fano # 1 forma dois loops reversos entre o centro e as bordas da superrede, e o campo magnético forma um loop no yz plano, correspondendo a um modo de ressonância TD ao longo do x eixo [44, 46]. Portanto, Fano # 1 surge do acoplamento ressonante entre os modos ED e TD, que estão em linha com os resultados previstos das decomposições multipolares conforme mencionado acima. Na verdade, devido às características ressonantes dos dipolos toroidais elétricos de Fano # 1, as distribuições de campo eletromagnético e corrente de deslocamento no pico ressonante (918,5 nm), comprimento de onda central (917,5 nm) e mergulho ressonante (916,5 nm) de Fano # 1 são quase iguais, exceto uma ligeira diferença na amplitude do campo (arquivo adicional 1:Fig. S1). No caso de Fano # 2, como mostrado na Fig. 4c, o campo elétrico é fortemente aumentado e a corrente de deslocamento forma dois loops reversos entre o centro da superrede e a superrede vizinha do PNS, indicando um modo de ressonância TD ao longo do z eixo. Além disso, o campo magnético de Fano # 2 é altamente localizado na superrede com a direção ao longo do y eixo, como mostrado na Fig. 4d, apresentando um modo ressonante MD. Como resultado, o Fano # 2 é a consequência direta do acoplamento ressonante dos dipolos toroidais magnéticos, o que está de acordo com a previsão das decomposições multipolares do campo distante do PNS. Além disso, devido ao acoplamento dos dipolos toroidais magnéticos de Fano # 2, o campo eletromagnético e a corrente de deslocamento no pico ressonante (771,1 nm), comprimento de onda central (772,0 nm) e mergulho ressonante (722,9 nm) de Fano # 2 mostram-se semelhantes distribuições (arquivo adicional 1:Figura S2).
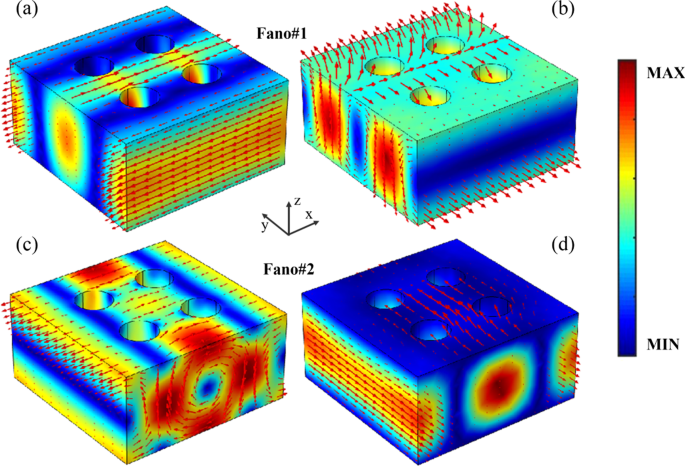
Distribuições de campo eletromagnético e corrente de deslocamento de ressonâncias de Fano da superrede do PNS, a barra colorida representa a amplitude do campo e as setas vermelhas indicam vetor de campo ou vetor de corrente de deslocamento. Outros parâmetros são iguais aos da Fig. 1c com Δ =- 28 nm. a e c Distribuições de amplitude de campo elétrico e vetor de corrente de deslocamento de Fano # 1 e Fano # 2, respectivamente. b e d Distribuições de amplitude de campo magnético e vetor de campo magnético de Fano # 1 e Fano # 2, respectivamente
Resultados e discussão
A Figura 5 mostra os espectros de transmissão do PNS em função do raio r do nanofuro, e outros parâmetros são os mesmos da Fig. 1c com Δ =- 28 nm. Conforme mostrado na Fig. 5a, as ressonâncias Fano de banda dupla podem ser mantidas como r varia de 0 ao valor máximo de 67,5 nm, i.e. , os orifícios tetramerizados são tangentes uns aos outros na superrede. O aumento do raio do nanofuro r aumenta as perturbações de superfície do PNS e reduz seu índice de refração efetivo (ERI) também, resultando no aumento do fator Q e no blueshift das ressonâncias de Fano. Especificamente, a localização ressonante de Fano # 1 é mais sensível à variação de r , e as ressonâncias Fano de banda dupla tendem a se fundir em um modo ressonante conforme os orifícios tetramerizados se aproximam. Conforme mostrado na Fig. 5b, o aumento de r não apenas altera a localização ressonante das ressonâncias de Fano, mas também aumenta seus FWHMs. Como r é aumentado de 25 para 45 nm, os picos ressonantes de Fano # 1 e Fano # 2 são desviados para o azul de 936,7 nm e 793,2 nm para 887,6 nm e 743,8 nm, respectivamente; e seus FWHMs são aumentados de 0,8 nm e 0,6 nm para 6,8 nm e 3,1 nm, respectivamente. Observe o aumento de r também melhora as profundidades de modulação das ressonâncias Fano, e profundidades de modulação de 100% podem ser realizadas como r é maior que 30 nm. Além disso, avaliando o deslocamento do pico de comprimento de onda de Fano afetado pelos parâmetros estruturais do PNS, é mostrado que o raio do nanofuro r são os parâmetros estruturais mais sensíveis para Fano # 1 e Fano # 2 (arquivo adicional 1:Figura S3). Portanto, a variação de r fornece uma abordagem eficaz para controlar dinamicamente as performances ressonantes das ressonâncias Fano de banda dupla do PNS.
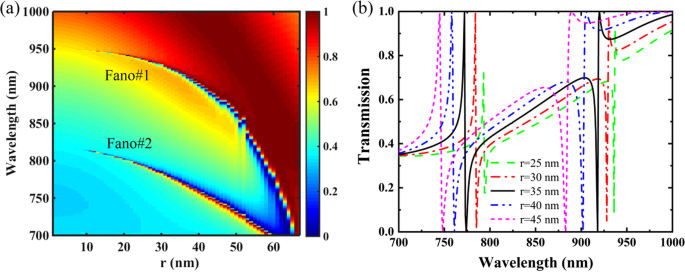
a Mapa de transmissão 2D do PNS em função do raio r do nanofuro. b Espectros de transmissão do PNS para diferentes raios de nanohol r . Outros parâmetros são iguais aos da Fig. 1c com Δ =- 28 nm
A Figura 6 mostra as influências da simetria da estrutura nas respostas de transmissão do PNS, onde o raio r ' de dois nanoholes varia de zero a tangente um ao outro, e outros parâmetros são os mesmos da Fig. 1c com Δ =- 28 nm. Como mostrado na Fig. 6a, para a superrede com simetria de espelho ao longo do x eixo (direção do campo elétrico da luz incidente), como o raio r ′ Dos dois nanoholes é aumentado, as localizações ressonantes das ressonâncias Fano de banda dupla são alteradas para o azul devido à diminuição no ERI do PNS, e suas larguras de banda são ampliadas devido ao aumento das perturbações da superfície. No entanto, como mostrado na Fig. 6b, embora as duas ressonâncias de Fano possam ser mantidas com o aumento de r ′, Duas ressonâncias Fano adicionais ocorrerão como a simetria espelhada da superrede ao longo do x eixo está quebrado. Em geral, quebrando a simetria estrutural ao longo do x ( y ) eixo também irá quebrar a simetria do modo ao longo do x ( y ) eixo de uma rede periódica, e o modo não degenerado não radiativo é capaz de acoplar à radiação externa devido ao seu componente degenerado [47]. Portanto, o fato de que as duas ressonâncias de Fano adicionais estão presentes apenas para a estrutura de simetria de espelho quebrada ao longo de x eixo indica que eles são devidos aos modos não degenerados perturbados.
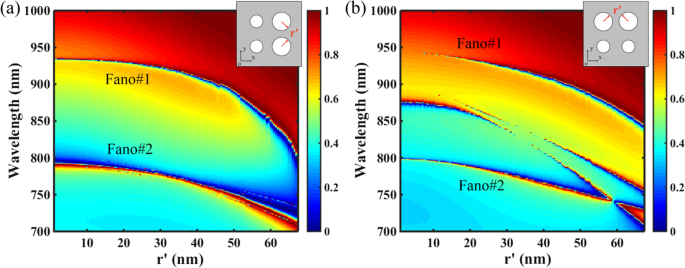
Influências da simetria da estrutura nas respostas de transmissão do PNS. Outros parâmetros são iguais aos da Fig. 1c com Δ =- 28 nm. As figuras inseridas indicam o diagrama esquemático da superrede do PNS. a Mapa de transmissão 2D do PNS em função do raio r ′ De dois nanoholes, onde a simetria estrutural da superrede ao longo do x eixo é mantido. b Mapa de transmissão 2D do PNS em função do raio r ′ De dois nanoholes, onde a simetria estrutural da superrede ao longo do x eixo está quebrado
Nós ainda caracterizamos os desempenhos ressonantes do PNS sob as influências do ângulo de incidência e do ângulo de polarização. Como mostrado na Fig. 7a, ressonâncias Fano de banda dupla do PNS são imunes à variação do ângulo de polarização devido ao C 4 topologia simétrica. Como o ângulo de polarização é alterado de 0 a 90 °, ou seja, de x -polarização para y -polarização, Fano # 1 e Fano # 2 são mantidos os mesmos. No entanto, no caso de ângulo incidente, como mostrado na Fig. 7b, embora Fano # 1 também seja insensível à variação do ângulo de incidente, Fano # 2 é desviado para o vermelho conforme o ângulo de incidência se desvia da incidência normal, e uma ressonância Fano adicional (Fano # 3) ocorre devido à supressão do decaimento da radiação do BIC protegido por simetria ser cancelada na incidência fora do normal. Em geral, este tipo de supressão de decaimento de radiação de BIC está intimamente relacionado à interferência destrutiva entre os campos de radiação emitidos de dois modos de vazamento de contra-propagação em qualquer uma das duas bordas da banda de parada das redes periódicas [48]. Observe que, devido ao forte acoplamento entre Fano # 2 e Fano # 3, uma janela de transparência induzida estreita pode ser excitada na região vizinha entre eles.
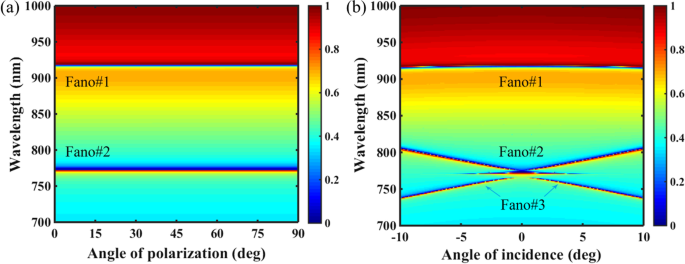
a Mapa de transmissão 2D do PNS em função do ângulo de polarização. b Mapa de transmissão 2D do PNS em função do ângulo de incidência. Outros parâmetros são iguais aos da Fig. 1c com Δ =- 28 nm
Finalmente, mostramos que múltiplas ressonâncias de Fano podem ser obtidas aumentando a altura H da laje do PNS. A Figura 8 mostra o mapa 2D de transmissão do PNS como funções de H para as estruturas não encolhidas (Δ =0 nm) e encolhidas (Δ =- 28 nm). Conforme mostrado na Fig. 8a, não há ressonância Fano, exceto as ressonâncias Fabry – Pérot (F – P) para o PNS não encolhido, pois H é variado. De acordo com a teoria F – P, a condição de ressonância da cavidade F – P do PNS não encolhido pode ser escrita como:
$$ \ delta =(2 \ pi / \ lambda) \ cdot H \ cdot n_ {ef} + \ varphi =m \ pi, $$ (8)
onde δ é a mudança de fase, λ é o comprimento de onda no espaço livre, n eff é o ERI da laje homogênea equivalente do PNS, φ é a fase adicional e m é um número inteiro que indica a ordem de ressonância. Usando a teoria do meio efetivo [49], o ERI do PNS pode ser estimado como:
$$ n_ {eff} =\ sqrt {\ frac {{\ left [{\ left ({1 - f} \ right) n_ {a} ^ {2} + fn_ {s} ^ {2}} \ right] \ left [{fn_ {a} ^ {2} + \ left ({1 - f} \ right) n_ {s} ^ {2}} \ right] + n_ {s} ^ {2}}} {{2 \ left [{fn_ {a} ^ {2} + \ left ({1 - f} \ right) n_ {s} ^ {2}} \ right]}}}, $$ (9)
onde f é o fator de preenchimento do PNS, e f =1 - 4π ( r / Λ) 2 .
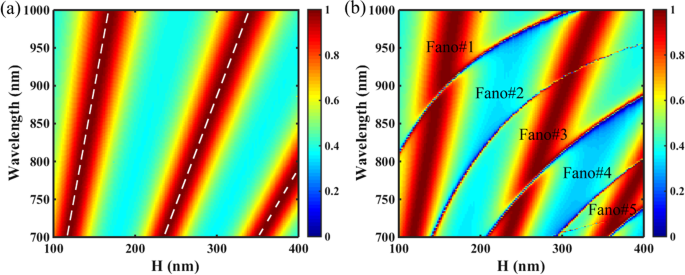
a Mapa de transmissão 2D do PNS em função da altura da laje H com Δ =0 nm, as linhas tracejadas brancas são os resultados do modelo de cavidade F – P. b Mapa 2D de transmissão do PNS em função da altura da laje H com Δ =- 28 nm. Outros parâmetros são iguais aos da Fig. 1c
Usando as Eqs. (8) e (9), as localizações da ressonância F – P do PNS não encolhido podem ser calculadas como λ F – P =2 π · H · n eff / ( mπ - φ ) No cálculo, embora a fase adicional φ não pode ser tratada como uma constante porque evidentemente afeta a mudança de fase δ , seus valores podem ser calculados usando o método de ajuste linear [50, 51]. A Figura 8a mostra o mapa 2D de transmissão do PNS com Δ =0 nm, e os resultados da teoria F – P são indicados pelas linhas tracejadas brancas. Conforme mostrado na Fig. 8a, as linhas tracejadas brancas do modelo de cavidade F – P coincidem com as dos picos de transmissão do PNS, confirmando que é a ressonância F – P que aumenta a transmissão do PNS não encolhido no região espectral de interesse. No entanto, como mostrado na Fig. 8b, para o PNS encolhido com Δ =- 24 nm, cinco ressonâncias Fano com alto fator Q são excitadas e coexistiram com as ressonâncias F – P conforme H varia na faixa de 100-400 nm , as ressonâncias Fano são tão fortes que dividem as ressonâncias F – P na região de cruzamento entre as ressonâncias Fano e F – P. De acordo com a teoria do guia de onda da placa, o aumento na espessura da placa de cristal fotônico garante mais modos de vazamento limitados na estrutura [32, 52]; assim, o número de ressonâncias de Fano pode ser aumentado simplesmente aumentando a espessura do PNS. Observe que a mudança dos orifícios tetramerizados não mudará o ERI do PNS, portanto, as localizações das ressonâncias F – P são mantidas quase as mesmas para as estruturas não reduzidas e reduzidas.
Conclusões
Ressonâncias Fano de banda dupla de fator Q alto podem ser realizadas usando uma arquitetura comparativamente simples de PNS com base na excitação de QBICs duplos. Reduzindo ou expandindo quatro nanoholes do PNS ao longo das diagonais da superrede, dois BICs protegidos por simetria podem ser transformados em ressonâncias Fano de banda dupla e suas localizações, bem como seus fatores Q podem ser ajustados de forma flexível. The dual-band Fano resonances of the PNS are resulted from the resonant couplings between the electric toroidal dipoles or the magnetic toroidal dipoles, and their correlations between the far-field multiple decompositions and the near-field distributions of the superlattice are verified. The dual-band Fano resonances of the PNS possess polarization-independent feature, and their high-Q-factor features are robust to the variations of the geometric parameters. By increasing the height of the PNS, the number of high-Q-factor Fano resonances can be improved as more leaky modes can be supported by the structure. Our results give more tuning freedoms for the realization of high-Q-factor resonators with better performances, which may provide a further step in the development of lasing, sensing and nonlinear photonics.
Disponibilidade de dados e materiais
Os conjuntos de dados usados e / ou analisados durante o estudo atual estão disponíveis junto ao autor correspondente, mediante solicitação razoável.
Abreviações
- Q-factor:
-
Quality factor
- PNS:
-
Planar nanohole slab
- BICs:
-
Bound states in the continuum
- NIR:
-
Near-infrared
- QBICs:
-
Quasi-BICs
- FWHM:
-
Full width at half maximum
- ED:
-
Electric dipole
- MD:
-
Magnetic dipole
- TD:
-
Toroidal dipole
- EQ:
-
Electric quadrupole
- MQ:
-
Magnetic quadrupole
- ERI:
-
Effective refractive index
- F–P:
-
Fabry–Pérot
Nanomateriais
- Os benefícios de usar pés niveladores em máquinas
- Sensores analógicos no Raspberry Pi usando um MCP3008
- Análise da causa raiz usando o método dos 5 porquês
- Usando ângulos para melhorar o futuro da eletrônica
- Markforged in the Classroom:Usando a impressão 3D na educação
- Como a IoT está perturbando o mundo ao nosso redor
- Os benefícios do uso de máquinas CNC
- Os benefícios de usar máquinas de nivelamento
- Os benefícios de usar um Sumitomo Inline Drive
- 74LS74:um guia completo do flip-flop duplo



