Estratégia de superfocagem de campo quase distante dependente da polarização de lentes plasmônicas baseadas em nanorregulação

Resumo

A superfocagem bidimensional de lentes plasmônicas baseadas em nanoreração (NRPLs) além do limite de difração na região de campo distante permanece um grande desafio em comprimentos de onda ópticos. Neste artigo, além da modulação de parâmetros estruturais, investigamos o desempenho de focalização dependente de polarização de um NRPL empregando o método de domínio de tempo de diferenças finitas (FDTD). Ao utilizar o estado de polarização (SOP) da luz incidente, percebemos com sucesso os focos de formato elíptico, de rosca e circular. As larguras totais mínimas na metade do máximo (FWHMs) desses focos são ~ 0,32, ~ 0,34 e ~ 0,42 λ ₀ no campo elétrico total, respectivamente, e a profundidade de foco (DOF) encontra-se em 1,41 ~ 1,77 λ ₀ . Esses focos de limite de sub-difração são bem controlados na região de campo quase distante. O mecanismo físico subjacente no deslocamento focal e uma forma eficaz de controlar a posição de foco são propostos. Além disso, no caso de uma abertura numérica alta, a componente longitudinal, que ocupa mais de 80% da energia do campo elétrico, decide os padrões de focalização dos focos. O foco de sub-limite de difração alcançado pode ser amplamente usado para muitas aplicações de engenharia, incluindo imagem de super-resolução, aceleração de partículas, processamento de informações ópticas quânticas e armazenamento óptico de dados.

Histórico

Junto com o desenvolvimento de imagens de super-resolução [1], aceleração de partículas [2], processamento de informações ópticas quânticas [3] e armazenamento de dados ópticos dependente de polarização [4], os dispositivos plasmônicos de superfície são amplamente aplicados nessas regiões modulando o ressonância de plasmon em uma magnitude de comprimento de onda. A lente plasmônica (PL), como um dispositivo típico, possui a capacidade de imagem perfeita que foi proposta pela primeira vez por J. B. Pendry em 2000 [5], e a imagem óptica sub-difração-limite foi experimentalmente demonstrada por X. Zhang et al. 5 anos depois [6]. No entanto, o plano de imagem foi confinado ao campo extremamente próximo à medida que as ondas evanescentes diminuem exponencialmente, indicando um campo óptico divergente. Esta limitação o torna impraticável para microscópios ópticos padrão [7].

Nos últimos anos, vários PLs baseados em nanoestrutura foram investigados [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Esses PLs podem não apenas realizar a focagem plasmônica no plano [8] ou no campo próximo [9], mas também podem possuir a capacidade de focagem no campo distante [10,11,12,13], que geralmente foram visualizados pela óptica de varredura microscópio [14]. No entanto, esses PLs mostraram uma grande dificuldade em realizar a focalização além do limite de difração, até que a relação de dispersão do guia de onda metal-isolante-metal (MIM) foi empregada para os PLs baseados em nanoslit para modular a fase na escala de sub comprimento de onda [11 , 15,16,17]. A modulação de fase precisa contribui para a linha focal do limite de sub-difração, e a luz polarizada linearmente é geralmente aplicada como a luz incidente para essas lentes. Mas, simplesmente estendendo o método de design semelhante de lentes nanoslit unidimensionais em duas dimensões, o foco de forma circular não pode ser realizado quando o PL rotacionalmente simétrico foi iluminado pela luz polarizada linearmente [18, 19], indicando a forte dependência de polarização do desempenho de foco. Além disso, o comprimento focal foi seriamente desviado do cálculo numérico de acordo com a teoria de reconstrução da frente de onda, especialmente para os PLs baseados em nanoring [18].

Os PLs baseados em nanoração com a simetria rotacional, que são denominados como lentes plasmônicas baseadas em nanoração (NRPLs) para simplificar na discussão a seguir, são reconhecidos como a substituição para as lentes refrativas conversacionais nos sistemas de focagem de sub comprimento de onda. Mas da perspectiva da excitação de polaritons de plasmon de superfície (SPPs), a luz polarizada linearmente é inadequada para os NRPLs, pois a eficiência de excitação é proporcional ao componente de campo elétrico radial da luz incidente. Comparativamente, a luz radialmente polarizada com a simetria cilíndrica em polarização se adapta à propriedade estrutural dos NRPLs [25]. Além disso, utilizando um batente de abertura em forma de donut [26, 27] ou placa de zona de Fresnel [28], esta luz polarizada foi aplicada para realizar o foco de forma circular de sub comprimento de onda. Assim, a luz radialmente polarizada foi geralmente aplicada como a luz incidente de NRPLs [20,21,22,23]. Comparado com a focagem de sub-comprimento de onda com o filtro espacial, esses PLs possuem a capacidade de modular a fase da luz incidente no guia de onda de sub-comprimento de onda. A excitação de ondas plasmônicas de superfície (SP) pode melhorar a transmissão de ondas eletromagnéticas. No entanto, a capacidade de superfocagem das lentes plasmônicas no campo distante não foi demonstrada. Além disso, embora o NRPL composto tenha sido proposto para modular o comprimento focal [24], o comprimento focal não foi efetivamente controlado e a energia do campo elétrico ainda está concentrada no centro da superfície final da lente.

Neste artigo, apresentamos o projeto teórico e o estudo numérico de um NRPL, com ênfase na realização da superfocagem utilizando a propriedade de polarização da luz incidente. Descrevemos o projeto teórico de NRPLs em nossa pesquisa e fornecemos o desempenho de foco na região de saída com base na simulação numérica no domínio do tempo de diferenças finitas (FDTD). Para investigar a dependência de polarização do desempenho de foco, as luzes polarizadas linearmente, circularmente, azimutalmente e radialmente são consideradas para iluminação. Discutimos os recursos de distribuição do campo elétrico na região de saída, incluindo a focagem do limite de sub-difração, as formas dos focos e a modulação do comprimento focal, e apontamos a importância da condição coaxial no desempenho da superfocagem.

Métodos

Os NRPLs investigados neste trabalho foram projetados usando a teoria de reconstrução da frente de onda, que foi amplamente aplicada aos PLs baseados em nanoslit [11, 15]. Para atingir o foco na posição desejada, o atraso de fase relativo causado quando a luz passa pelo i - o nanooreamento individual precisa satisfazer a seguinte condição com base na ótica geométrica:
$$ - \ varDelta \ phi \ left ({r} _i \ right) =\ frac {2 \ pi \ sqrt {f_0 ^ 2 + {r} _i ^ 2}} {\ lambda_0} - \ frac {2 \ pi \ sqrt {f_0 ^ 2 + {r} _1 ^ 2}} {\ lambda_0} +2 n \ pi $$ (1)
onde −Δ ϕ ( r _i ) é a diferença de fase relativa entre o primeiro nanoramento no centro interno e o i -th nanoring, r é o raio, λ ₀ é o comprimento de onda do espaço livre da luz incidente, n é um número inteiro arbitrário e f ₀ é a distância focal projetada.

O elemento básico que compreende os NRPLs pesquisados ​​são os nanorings padronizados no filme metálico. De acordo com a Ref. [29], quando o diâmetro é maior do que o comprimento de onda da luz incidente, o nanoreamento de ar cercado por paredes metálicas pode ser aproximado ao modelo de guia de onda MIM como o inset ilustra na Fig. 1. O atraso de fase é definido principalmente pela parte real da constante de propagação β , expresso como Re ( β ) • t , onde t é a espessura do nanoring. Com base na relação de dispersão, a constante de propagação complexa β pode ser calculado como:

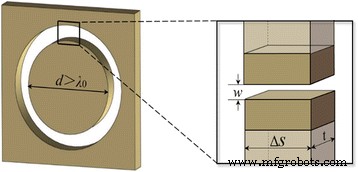
O modelo de guia de onda MIM de um nanoring individual embutido no filme de ouro. A inserção dá uma visão ampliada de uma pequena porção arbitrária do nanoring
$$ \ tanh \ left (\ frac {w \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _d}} {2} \ right) =- \ frac {\ varepsilon_d \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _m}} {\ varepsilon_m \ sqrt {\ beta ^ 2- {k} _0 ^ 2 {\ varepsilon} _d}} $$ (2)
onde k ₀ representa o vetor de onda no vácuo e ε _d e ε _m são a permissividade do dielétrico e do metal, respectivamente. Baseie-se na Eq. (2), podemos ver que a constante de propagação β depende da largura de um nanoring. Assim, para a lente plana com uma dada espessura t , o atraso de fase causado é simplesmente determinado pela largura w do nanoramento individual quando a luz passa por ele. Em nossa pesquisa, o dielétrico é definido para ser o ar com a permissividade ε _d =1, e o filme de ouro com uma espessura t de 400 nm, cuja permissividade no comprimento de onda incidente de 650 nm é ε _m =−12,8915 + 1,2044i [15]. Além disso, como relatamos anteriormente [16], o efeito de acoplamento das luzes de propagação nos dois guias de onda MIM adjacentes também desempenha um papel importante no atraso de fase, especialmente quando o espaçamento da parede metálica é menor que o dobro da profundidade da pele δ _m , que pode ser estimado por [30]:
$$ {\ delta} _m =\ frac {1} {k_0} {\ left | \ frac {\ mathrm {Re} \ left ({\ varepsilon} _m \ right) + {\ varepsilon} _d} {\ mathrm { Re} {\ left ({\ varepsilon} _m \ right)} ^ 2} \ right |} ^ {\ frac {1} {2}} $$ (3)
Consequentemente, a profundidade de pele calculada δ _m é cerca de 28 nm. Ao considerar o efeito de acoplamento, um PL baseado em nanoslit com a capacidade de superfocagem de 0,38 λ ₀ na resolução foi relatado em nossa pesquisa anterior [16]. Aqui, para analisar de forma proeminente a influência do estado de polarização (SOP) no desempenho de focagem, as paredes de espaçamento entre dois nanorings adjacentes são projetadas para ter 100 nm, muito maior do que 2 δ _m para eliminar o efeito de acoplamento.

O esquema do NRPL projetado é mostrado na Fig. 2, e um número total de 32 nanorings concêntricos são incluídos para reconstruir a frente de onda. A largura do nanoring para a faixa de modulação de fase desejada de 10 a 100 nm. A distância focal desejada f ₀ é 1300 nm (2 λ ₀ ) Para utilizar de forma eficiente o modelo de guia de onda MIM, o diâmetro mínimo do nanorimento interno é definido como 800 nm. Além disso, para evitar o deslocamento focal como discutido em nosso trabalho anterior [15], a diferença de fase total é tão grande quanto 10π, com uma abertura numérica prevista (NA) de 0,96. Como resultado, o limite de difração de Rayleigh teórico, calculado por 0,61 λ ₀ / NA [31], é 413 nm (~ 0,64 λ ₀ )

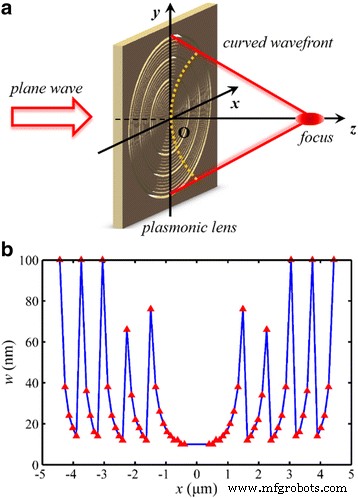
Esquema do NRPL. a A luz incidente normalmente ilumina as lentes. b Parâmetros estruturais da lente. Os valores das coordenadas dos triângulos vermelhos representam o raio r e largura w do nanoramento correspondente

Para investigar as influências SOP da luz incidente nas distribuições de intensidade espacial, especialmente o desempenho de foco, o NRPL projetado foi iluminado pela luz polarizada linearmente, circularmente, azimutalmente e radialmente, respectivamente. Todos os casos foram calculados pelas simulações numéricas do FDTD. De acordo com a ótica da matriz, as diferentes luzes polarizadas podem ser descritas pelos formalismos da matriz de Jones, e a expressão da matriz correspondente foi aplicada para definir a luz incidente. O limite do modelo era a camada perfeitamente combinada (PML) com um número de camada 12. Para equilibrar a precisão computacional e o consumo de memória nas simulações, o tamanho da malha foi definido como 10 nm na região de saída e 5 nm em torno do região focal.

Resultados

I Polarização Linear

Para a luz linearmente polarizada, o SOP é espacialmente homogêneo e, neste caso, a direção do vetor elétrico é paralela ao x eixo. Quando a luz ilumina o NRPL, existem dois focos, distribuindo 400 nm de distância um do outro no campo elétrico total | E | ² conforme apresentado na Fig. 3. Embora as larguras totais na metade do máximo (FWHMs) de ambos sejam de 210 nm (~ 0,32 λ ₀ ) no plano focal, o resultado da simulação indica que a distribuição de intensidade é aparentemente diferente do projeto baseado na teoria de reconstrução da frente de onda, onde deve haver um foco do tipo circular exatamente no z eixo (também chamado de eixo óptico).

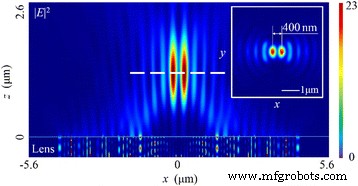
Padrão de distribuição de intensidade do campo elétrico total | E | ² no caso de luz incidente linearmente polarizada. A inserção mostra o padrão de intensidade no plano focal. A distância focal é de 1215 nm (um desvio de 6,54%). Os FWHMs de ambos os focos são ~ 0,32 λ ₀ , com 400 nm de distância um do outro, e a profundidade de foco (DOF) é de ~ 1,68 λ ₀

Para analisar as diferenças entre a simulação e o projeto teórico, as distribuições de intensidade dos componentes do campo elétrico são investigadas. Conforme apresentado na Fig. 4, aparece um foco de forma elíptica e o FWHM em x- e y- direção é 220 nm (~ 0,34 λ ₀ ) e 457 nm (~ 0,70 λ ₀ ), respectivamente. Este padrão concorda bem com os resultados experimentais da Ref. [18] onde a mesma luz polarizada foi aplicada. No entanto, a simulação mostra que o padrão de distribuição de | E | ² é semelhante ao padrão do componente longitudinal | E _z | ² que ocupa 79,8% da energia elétrica total. Portanto, a diferença é atribuída principalmente à distribuição extraordinária de | E _z | ² .

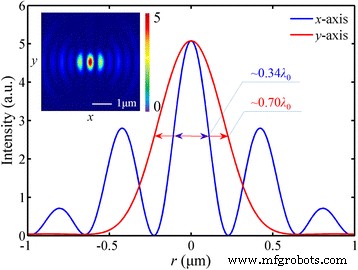
Distribuição de intensidade da componente transversal | E _r | ² no plano focal. A inserção mostra o foco de forma elíptica. O comprimento focal é 1425 nm (um desvio de 9,62%). | E _r | ² ocupa 20,2% da energia elétrica total. O DOF é ~ 1,41 λ ₀

Em última análise, este fenômeno pode ser explicado pela propriedade de transmissão do NRPL. Por outro lado, a excitação de SPPs nas interfaces de metal e dielétrico geralmente depende da direção de polarização local da luz incidente. As ondas elétricas transversais (TE) não podem contribuir para a excitação. Por outro lado, devido à estrutura de comprimento de onda do guia de onda MIM, apenas as ondas SP podem se propagar através desta lente [32]. Com a simetria rotacional da lente, o componente magnético transversal local (TM) muda com o ângulo azimutal θ na forma cosinoidal. Portanto, como mostrado na Fig. 5a, a distribuição de intensidade de | E | ² , que está logo acima da superfície final da lente, está concentrada próximo a y =Região 0 (−π / 4 < θ <Π / 4). Correspondentemente, os vetores de Poynting se propagam ao longo da direção radial na superfície da extremidade, conforme apresentado na Fig. 5b. Assim, a direção do vetor de E é basicamente paralelo ao eixo óptico, que forma o conteúdo principal de E _z . Devido à interferência simetricamente construtiva, aparecem dois focos no plano focal em vez de um foco do tipo circular.

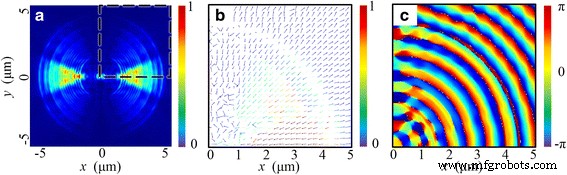
As propriedades de distribuição do campo elétrico na seção transversal apenas 50 nm acima da superfície final da lente. a Distribuição de intensidade normalizada de | E | ² . b A distribuição do vetor de Poynting dentro da linha tracejada região em a. c A distribuição de fase correspondente de E _z

II Polarização Circular

Como o estado da luz polarizada circularmente muda com o tempo periodicamente, os resultados simulados são a distribuição de campo com média de tempo. Quando a lente é iluminada por esta luz polarizada, forma um foco em formato de rosca em | E _z | ² . Conforme mostrado na Fig. 6a, o comprimento focal neste campo é 1185 nm, mostrando um desvio de 8,85% em relação ao valor projetado. A largura do donut é de 210 nm (~ 0,32 λ ₀ ) e o raio é de 400 nm. A profundidade de foco (DOF) é de ~ 1,65 λ ₀ . O peso de | E _z | ² é 80,6% da energia elétrica total. Além disso, em | E _r | ² , a superposição no domínio espacial gera um foco circular com o comprimento focal de 1405 nm (um desvio de 8,08%). O FWHM é 295 nm (~ 0,45 λ ₀ ) neste campo, e o DOF é ~ 1,68 λ ₀ . Além disso, ambos os padrões de distribuição em r-z plano assemelham-se aos do x - z plano no caso de luz incidente linearmente polarizada. Levando em consideração o componente de campo elétrico radial, o FWHM pode ser reduzido para 222 nm (~ 0,34 λ ₀ )

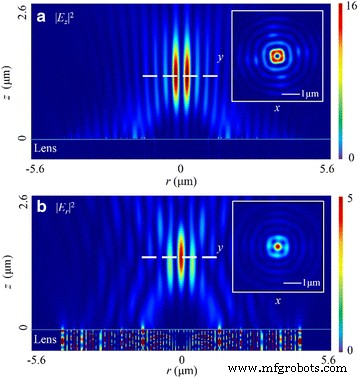
Padrões de distribuição de intensidade de | E _z | ² e | E _r | ² em r-z plano no caso de luz polarizada circularmente. a Em | E _z | ² , o FWHM, DOF e o comprimento focal é ~ 0,32 λ ₀ , ~ 1,65 λ ₀ e 1185 nm, respectivamente. b Em | E _r | ² , o FWHM, DOF e o comprimento focal é ~ 0,45 λ ₀ , ~ 1,68 λ ₀ e 1405 nm, respectivamente

III Polarização azimutal

Para a luz incidente azimutalmente polarizada, os vetores elétricos são perpendiculares à direção radial, que são paralelos à interface ouro / vácuo do NRPL. À medida que a luz polarizada azimutalmente ilumina a lente, as ondas TE locais falham em excitar os SPPs na interface. Assim, a distância de transmissão em nanorings é proporcional às suas larguras, conforme apresentado na Fig. 7. Como a estrutura e a iluminação são de simetria rotacional, apenas metade do padrão de distribuição de intensidade e a estrutura do NRPL são mostradas. A luz transmitida pode ser desprezada e não há um foco distinto na região de saída.

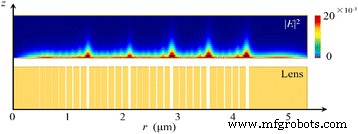
Padrão de distribuição de intensidade na região da lente e sua vista em corte transversal. A distância de transmissão das ondas não SP em nanorings é proporcional à largura da fenda

Polarização radial IV

Correspondendo à luz polarizada azimutalmente, a luz polarizada radialmente pode ser considerada como a onda TM local, e esta propriedade de polarização corresponde à condição de excitação de SPPs, o que contribui para uma maior intensidade máxima no foco. No campo elétrico total E , a intensidade máxima é cinco vezes maior do que para a luz incidente linearmente polarizada. Além disso, há um foco de forma circular com 276 nm (~ 0,42 λ ₀ ) FWHM em | E | ² , como mostrado na Fig. 8. A distribuição de intensidade simulada é muito semelhante à capacidade de foco das lentes refrativas de alto NA [33]. Além disso, esse desempenho de foco ainda depende de | E _z | ² , que ocupa 82,0% da energia elétrica total.

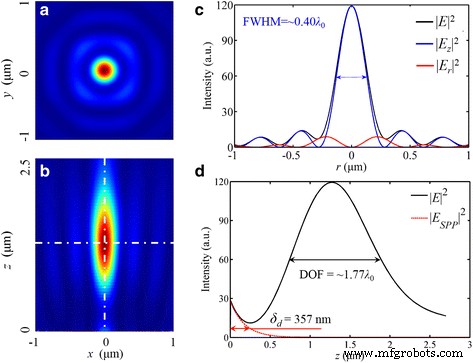
Distribuição de intensidade de | E | ² no caso de luz incidente radialmente polarizada. a , b A distribuição no plano focal e em x - z corte transversal. c O perfil de intensidade na direção radial. d O perfil de intensidade ao longo do eixo óptico onde a linha sólida preta é a distribuição total da intensidade do campo elétrico na simulação e a linha tracejada vermelha é a curva calculada de SPP. A distância focal é de 1275 nm (um desvio de 1,92%). O FWHM de | E | ² e | E _z | ² é 272 nm (~ 0,42 λ ₀ ) e 260 nm (~ 0,40 λ ₀ ), respectivamente. O DOF é ~ 1,77 λ ₀

Diferente dos casos anteriores, há um foco de forma circular em | E _z | ² . Além disso, este componente também determina o padrão de distribuição em | E | ² . Conforme apresentado na Fig. 9a, o FWHM em | E _z | ² é 260 nm (~ 0,40 λ ₀ ), que é próximo ao da linha focal no caso de PL baseado em nanoslit [16]. Particularmente, o comprimento focal é de 1275 nm. Comparado com o valor projetado, o erro relativo diminui para 1,9%. No entanto, a distância focal é 1455 nm (um desvio de 11,2%) em | E _r | ² . Conforme apresentado na Fig. 9b, há um foco em forma de donut com largura de 227 nm (~ 0,35 λ ₀ ) nesta área. O DOF é ~ 1,60 λ ₀ .

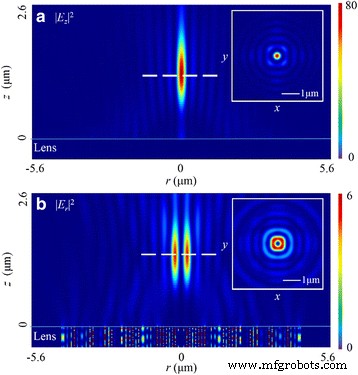
Padrões de distribuição de intensidade de | E _z | ² e | E _r | ² em r-z plano no caso de luz radialmente polarizada. a | E _z | ² padrão no r-z avião. A inserção mostra um foco de forma circular no plano focal. b O transversal | E _r | ² padrão no r-z avião. A inserção mostra um foco em formato de rosquinha no plano focal

O atraso de fase das ondas SP em nanorings é investigado, conforme apresentado na Fig. 10. A simulação indica que a modulação de fase é dramaticamente influenciada pelos parâmetros estruturais do NRPL e os atrasos de fase simulados entre a superfície incidente e a superfície de saída são basicamente idênticos aos valores calculados com base na Eq. (2) Na superfície final da lente, as ondas SP ainda se propagam ao longo da direção radial e existe um ponto quente no centro da superfície, cuja intensidade é um quinto da intensidade do foco. A interferência construtiva das ondas SP, com a distribuição simétrica rotacional, constrói as ondas propagadas e realiza o foco de forma circular no campo quase distante.

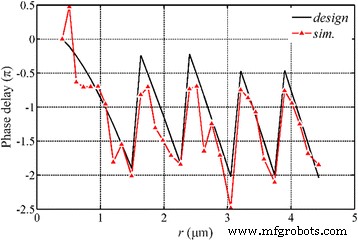
Análise de fase do NRPL sob a luz incidente radialmente polarizada

Discussões

I Capacidade de superfocagem de NRPLs

Conforme as luzes incidentes com diferentes SOPs são aplicadas, incluindo as polarizações linear, circular e radial, os focos de limite de sub-difração podem ser realizados. Embora a forma do foco seja influenciada pelo SOP, os tamanhos característicos desses focos superam o limite de difração de Rayleigh (413 nm). Os resultados da simulação demonstram com sucesso a capacidade de superfocagem do NRPL, e a distribuição de intensidade no plano focal é semelhante à função de Bessel que é usada para descrever o feixe de não difração.

Para o caso da luz incidente radialmente polarizada, como um exemplo mostrado na Fig. 11, a distribuição de intensidade em | E _z | ² é idêntico à função de Bessel de ordem zero J ₀ ( K _spp ⋅ n ⋅ r ), onde n e r é o índice de refração do meio ambiental e a distância radial ao eixo óptico, respectivamente. O FWHM do foco é ligeiramente maior do que o tamanho do lobo principal calculado com J ₀ . Particularmente, as simulações indicam que o feixe de não difração pode ser realizado no campo quase distante. As ondas SP, como uma espécie de onda evanescente, diminuem exponencialmente quando se propagam para longe da superfície de saída, e a distância de propagação no vácuo pode ser calculada por [30]:

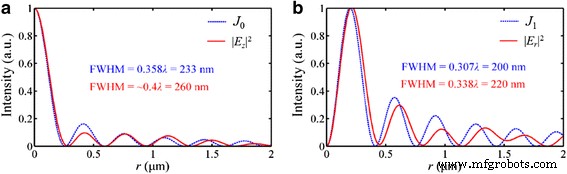
Perfis de intensidade do NRPL no plano focal sob a luz incidente radialmente polarizada. a A distribuição de | E _z | ² assemelha-se à função de Bessel de ordem zero J ₀ . b A distribuição de | E _r | ² assemelha-se à função de Bessel de primeira ordem J ₁
$$ {\ delta} _d =\ frac {1} {k_0} {\ left | \ frac {\ mathrm {Re} \ left ({\ varepsilon} _m \ right) + {\ varepsilon} _d} {{\ varepsilon_d } ^ 2} \ right |} ^ {\ frac {1} {2}} $$ (4)
onde ε _d e ε _m são a permissividade do dielétrico e do metal, respectivamente. Assim, δ _d é 357 nm, o que é consistente com a simulação mostrada na Fig. 8d. Portanto, a intensidade das ondas SP no foco pode ser desprezada na região de campo quase distante.

II Forma de foco

Ao modular o SOP, os focos em formato elíptico, circular e donut podem ser realizados no plano focal, conforme apresentado na Fig. 12. O fenômeno é atribuído ao tamanho focal do sub comprimento de onda, e não podemos perceber o tipo circular concentre-se em campos elétricos e magnéticos ao mesmo tempo. Assim, um foco do tipo donut é realizado nos campos magnéticos (ou elétricos), enquanto um foco do tipo circular é obtido no campo correspondentemente elétrico (ou magnético). Particularmente, porque não há campo magnético longitudinal, a distribuição de intensidade de | H | ² é o mesmo que o padrão de | E _r | ² . Além disso, | E _z | ² ocupa cerca de 80,0% da energia elétrica total e a escala não é afetada pelos POPs da luz incidente.

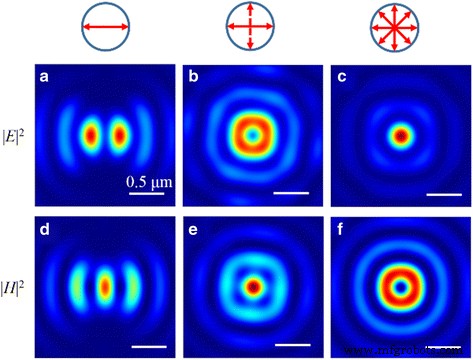
Os padrões de intensidade normalizados do campo elétrico | E | ² e campo magnético | H | ² no plano focal quando o NRPL é iluminado pela luz polarizada. a | E | ² e d | H | ² distribuição com luz incidente linearmente polarizada. b | E | ² e e | H | ² distribuição com luz incidente circularmente polarizada. c | E | ² e f | H | ² distribuição com luz incidente radialmente polarizada

III Modulação do comprimento focal

A distância focal simulada em diferentes casos é basicamente próxima à posição desejada f ₀ (1300 nm), conforme mostrado na Tabela 1. Mas, percebemos que o comprimento focal no campo transversal | E _r | ² é cerca de 200 nm mais longo do que no campo longitudinal | E _z | ² , independentemente do SOP da luz incidente e o desvio normalmente existe.

Em teoria, a teoria de reconstrução da frente de onda é adequada para projetar o NRPL com uma distância focal arbitrária do campo próximo à região do campo distante. No entanto, se a distância focal real de uma lente plasmônica projetada concorda bem com a distância focal projetada depende da diferença de fase total da lente. O desvio pode ser atribuído à distinção entre o foco do tipo amplitude e o foco do tipo fase [34]. Como a modulação de fase no guia de onda MIM visa o componente radial, o comprimento focal em | E _r | ² pode ser modulada pela teoria de reconstrução da frente de onda, quando a diferença de fase total de pelo menos 2π é satisfeita [15]. Para o componente longitudinal, uma diferença de fase total maior (> 10π) é vantajosa para a consistência. Conforme mostrado na Fig. 13, quando a diferença de fase aumenta de 2π para 16π, correspondentemente o NA de 0,75 a 0,96, o foco do tipo amplitude em | E _z | ² move-se da superfície de saída da lente para a posição desejada. Como a distribuição de intensidade de | E | ² é decidido por | E _z | ² , o NA pode influenciar dramaticamente o comprimento focal no campo elétrico total. No entanto, a alteração do comprimento focal em | E _z | ² diminui gradualmente, junto com o aumento da diferença de fase total. Por outro lado, a posição do foco do tipo de fase em | E _r | ² é relativamente estável. Quando o NRPL com um NA alto é aplicado, ainda há um desvio na distância focal derivada com base na distribuição de intensidade de | E _x | ² e | E _z | ² , e o desvio quase se mantém invariável. Portanto, o comprimento focal dos NRPLs pode ser efetivamente controlado pela modulação de fase e otimização estrutural, embora o mesmo comprimento focal não possa ser alcançado nos campos de componente transversal e longitudinal.

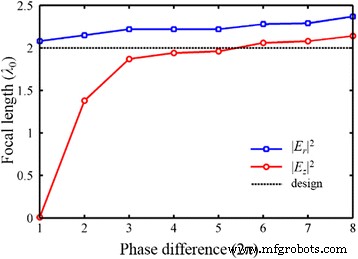
A distância focal do NRPL com o aumento da diferença de fase total de 2π para 16π

IV Focusing Performace in the Non-Coaxial Situation

The non-coaxial situation is a common problem in the experiment, and its effect on the focusing performance should be considered. As shown in Fig. 14, the center of the radially polarized light deviates 3 μm from the optical axis of the NRPL along the x eixo. Compared with Figs. 8 and 9, the intensity distributions both in x-z cross section and in focal plane are apparently changed. In the longitudinal electric field, an elliptical focus is located at 1340 nm away from the exit surface of the lens. The FWHMs in x-z and y-z planes are 0.51 and 0.38 λ ₀ , respectivamente. On the other hand, the distribution in transverse field is also distorted, where the intensity of one side lobe is higher than the other one. Furthermore, compared with the coaxial condition, the decrease of the maximum intensity in the total electric field is more than 85%.

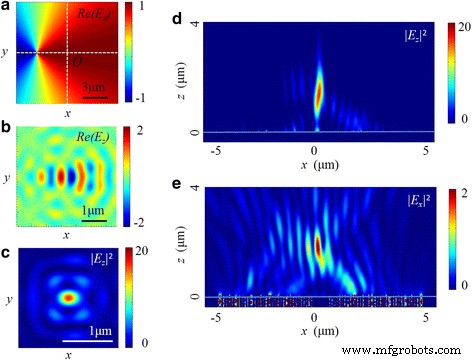
The intensity distribution of the NRPL in the non-coaxial situation. a The real part of E _x of radially polarized incident light. b , c The distribution of Re(E _z ) and |E _z | ² in the focal plane. d , e The distribution of |E _z | ² and |E _x | ² in the x-z avião

The preliminary simulation indicates that the non-coaxial situation indeed influences the intensity distribution and the desired focusing performance of lens. Therefore, it is essential to guarantee the coaxiality between the incident light and the lens center during the experiment.

Conclusions

In summary, we build a NRPL with a high NA utilizing the wavefront reconstruction theory and the dispersion relation of the MIM waveguide. We also investigate the polarization-dependent focusing performance in the quasi-far field, including the focal length, FWHM, DOF, and the maximum intensity. The conventional polarized light, such as the linearly, circularly, radially, and azimuthally polarized light, are all considered. The simulations demonstrate the superfocusing capability of the designed NRPL. Utilizing the polarization-dependent property, the sub-diffraction-limit elliptical-, circular-, and donut-shape foci can be realized. However, one limitation of this work is that the proposed design strategy to realize the superfocusing performance of NRPLs is aimed for the quasi-far-field region, although to the best of our knowledge, the similar focusing capability in this region is rarely reported. In addition, we discover the underlying physical phenomenon on the focal shift and propose a more effective way to control the focusing position by employing both the transverse and longitudinal fields. There are considerable engineering applications for the nanoring-based superfocusing lenses, ranging from the super-resolution imaging, particle acceleration, quantum optical information processing to the optical data storage.

Abreviações

DOF:

Depth of focus

FDTD:

Domínio do tempo de diferença finita

FWHM:

Full-width at half maximum

MIM:

Metal-insulator-metal

NRPL:

Nanoring-based plasmonic lenses

PML:

Perfectly matched layer

SOP:

State of polarization

SPPs:

Surface plasmon polaritons

TE:

Transverse electric

TM:

Magnético transversal

Compostos de grafeno e polímero para aplicações de supercapacitor:uma revisão Desvendando a evolução morfológica e cinética de corrosão de nanofios de silício poroso durante a corrosão química assistida por metal