Propriedades da fase geométrica em oscilações eletromecânicas de ressonadores nanofios baseados em nanotubos de carbono

Resumo

A fase geométrica é uma evolução de fase extra na função de onda das vibrações que é potencialmente aplicável em uma ampla gama de ciência e tecnologia. As características da fase geométrica no estado comprimido para um ressonador nanofio baseado em nanotubos de carbono foram investigadas por meio do método do operador invariante. A introdução de um operador invariante linear, que é útil para tratar um sistema hamiltoniano dependente do tempo complicado, nos permitiu derivar a fórmula analítica da fase geométrica. Fazendo uso disso, analisamos o comportamento temporal da fase geométrica com base em ilustrações relevantes. A influência dos parâmetros de compressão na evolução da fase geométrica foi investigada. A fase geométrica, em geral, oscila, e o envelope de tal oscilação aumenta com o tempo. A taxa de aumento da fase geométrica é grande quando os parâmetros, como a amplitude clássica da oscilação, o fator de amortecimento e a amplitude da força motriz, são grandes. Confirmamos um aumento muito acentuado da fase geométrica ao longo do tempo no caso em que a frequência angular do sistema chega perto da frequência angular de ressonância. Nosso desenvolvimento em relação às características da fase geométrica é crucial para o entendimento das características topológicas nas oscilações dos nanofios.

Introdução

Vibrações mecânicas dos menores ressonadores, como nanofios baseados em nanotubos de carbono (baseados em CNT) [1-3], nanofios semicondutores [4], grafenos [5] e partículas levitadas [6], têm sido um assunto principal de pesquisa na comunidade da nanociência há mais de uma década. Pesquisas ativas relacionadas às oscilações eletromecânicas de ressonadores de nanofios impulsionadas por uma força periódica externa foram realizadas nas esferas teórica e experimental. Em particular, ressonadores nanofios baseados em CNT têm atraído considerável interesse como dispositivos mecânicos em nanoescala devido às suas sensibilidades extraordinárias com fatores de alta qualidade a uma pequena perturbação dos arredores. Ressonadores de nanofios baseados em CNT suspensos são candidatos promissores para aparelhos que medem uma ampla gama de grandezas físicas, como ondas EM [2], pequenas forças [7], massas [8], temperaturas [9] e ruídos [10].

As análises da evolução da fase quântica em oscilações de nanofios são necessárias para elucidar as características subjacentes do sistema teoricamente. Em relação aos estados vibracionais quânticos dos ressonadores nanofios baseados em CNT [11], a fase geométrica [12], bem como a fase dinâmica usual, surgem como uma evolução suplementar da fase. A fase geométrica [12] é uma anholonômica de um estado quântico que pode ser aplicável em diversos campos da física. Análises da fase geométrica podem ser potencialmente adotadas na caracterização de nano propriedades de nanofios, como os perfis de ressonância [13, 14], fortes vibrações quânticas [15, 16], mecanismos de relaxação de deformação [17, 18], o surgimento de magnetoplasmons de Dirac [19], e a topologia das oscilações de Aharonov-Bohm [20].

O estudo da fase geométrica associada à dinâmica não-adiabática pode fornecer uma visão para sistemas nanomecânicos, que é necessária para o avanço de técnicas de simulação precisas [21]. A preparação, manipulação e detecção de estados quânticos são fatores importantes nas tecnologias quânticas. O objetivo da presente pesquisa é lançar luz sobre os comportamentos temporais da fase geométrica que ocorre em estados quânticos de oscilações de nanofios. Para entender o mecanismo de vibrações de nanofios baseados em CNT, investigaremos a evolução temporal da fase geométrica no estado comprimido, que é um estado quântico clássico, como o estado coerente. O mérito do estado comprimido é que a incerteza de uma quadratura nesse estado pode ser reduzida substancialmente às custas do aumento da incerteza da outra quadratura, enquanto tal modulação de incerteza é impossível no estado coerente. Em particular, iremos analisar os efeitos da ressonância na fase geométrica. Como a energia ressonante é significativamente diferente da energia do estado não ressonante [22, 23], o comportamento topológico da função de onda não é trivial e pode ser consideravelmente desviado daquele em situações normais. A influência da mudança dos parâmetros físicos e dos parâmetros de compressão na evolução da fase geométrica também será rigorosamente analisada. As fases geométricas são ubíquas em sistemas dinâmicos [24] e podem ser aplicadas a várias tecnologias modernas, como computação quântica [25], interferometria de intensidade [26], multitarefa fotônica [27], protocolos de detecção quântica [28] e onda -medidas de estabilidade [29].

O hamiltoniano do sistema envolve funções de tempo associadas ao amortecimento do sistema e à força motriz externa. Conseqüentemente, o sistema é um tipo de sistema hamiltoniano dependente do tempo (TDHSs), dos quais problemas de mecânica quântica são extensivamente estudados até recentemente. A função de tempo no hamiltoniano de um TDHS não pode ser separada da função de variáveis canônicas na maioria dos casos, fazendo com que o método convencional de separação de variáveis para resolver a equação de Schrödinger não esteja disponível. Um método alternativo poderoso desenvolvido para superar esta dificuldade é o método do operador invariante que foi introduzido por Lewis e Riesenfeld [30, 31]. Este método é uma ferramenta matemática muito útil quando derivamos soluções quânticas de um TDHS. Muitos problemas de mecânica quântica descritos por TDHSs são investigados com base neste método. Por exemplo, eles incluem espalhamento caótico de partículas [32], propagação de luz em meios que variam no tempo [33], controle de elétrons conduzidos presos [34] e não-clássica de circuitos nanoeletrônicos quânticos [35]. Há uma variedade de outros métodos para tratamentos de mecânica quântica de TDHSs, que incluem o método de transformação unitária [36], o método algébrico de Lie [37] e o método de estimativa hamiltoniano [38].

Considerando que o sistema é um TDHS, usamos o método do operador invariante para obter soluções quânticas do sistema. Um operador linear invariante que é representado em termos do operador de aniquilação será introduzido. Enquanto os operadores de aniquilação e criação são representados em termos de tempo devido à dependência de tempo do sistema, os estados coerente e comprimido podem ser obtidos usando esses operadores de escada. A fase geométrica do sistema será avaliada analiticamente utilizando a função de onda no estado comprimido. A evolução temporal da fase geométrica será analisada em detalhe com base nas suas ilustrações representadas com diversas escolhas de parâmetros.

Métodos

Para investigar a fase geométrica, primeiro precisamos configurar a equação clássica de movimento da ponta do nanofio. Como a fase geométrica aparece na evolução da onda quântica de um TDHS, é necessário derivar funções de onda em um estado quântico específico que gerenciamos. Iremos considerar o estado comprimido conforme mencionado na parte introdutória. As funções de onda nos diversos estados quânticos de um TDHS, incluindo o estado comprimido, podem ser obtidas a partir do método do operador invariável.

A equação do movimento para a amplitude dependente do tempo x para um modo de dobra de um nanotubo de carbono suspenso com uma massa efetiva m é dado por [1]
$$ \ ddot {x} + \ left (\ frac {\ omega_ {0}} {Q} + \ eta x ^ {2} \ right) \ ponto {x} + \ left (\ omega_ {0} ^ { 2} + \ beta x ^ {2} \ right) x =f _ {\ mathrm {d}} \ cos (\ omega t), $$ (1)
onde ω ₀ é a frequência angular ressonante, Q o fator de qualidade, f _d a força motriz eletrostática dividida por m , η o coeficiente de amortecimento não linear, e β o parâmetro Duffing. Vamos supor, por conveniência, que o deslocamento da ponta seja suficientemente pequeno em relação ao comprimento do fio CNT. Então, podemos negligenciar os termos não lineares na Eq. (1), levando a [2]
$$ \ ddot {x} + \ frac {\ omega_ {0}} {Q} \ ponto {x} + \ omega_ {0} ^ {2} x =f _ {\ mathrm {d}} \ cos (\ omega t). $$ (2)
O hamiltoniano do sistema que produz a Eq. (2) é dado por
$$ \ hat {H} =e ^ {- \ gamma t} \ frac {\ hat {p} ^ {2}} {2m} + \ frac {1} {2} me ^ {\ gamma t} \ left [\ omega_ {0} ^ {2} \ hat {x} ^ {2} - 2f _ {\ mathrm {d}} \ cos (\ omega t) \ hat {x} \ right], $$ (3)
onde γ = ω ₀ / Q . A solução clássica da Eq. (2) é composto por uma função complementar X _c ( t ) e uma solução particular X _p ( t ), que são fornecidos por
$$ \ begin {array} {@ {} rcl @ {}} &&X_ {c} (t) =X_ {c, 0} e ^ {- \ gamma t / 2} \ cos (\ Omega t + \ varphi) , \ end {array} $$ (4) $$ \ begin {array} {@ {} rcl @ {}} &&X_ {p} (t) =X_ {p, 0} \ cos (\ omega t - \ delta), \ end {array} $$ (5)
onde X _{c , 0} é uma constante, \ (\ Omega =\ sqrt {\ omega _ {0} ^ {2} - \ gamma ^ {2} / 4} \), φ é uma fase arbitrária, e
$$ \ begin {array} {@ {} rcl @ {}} X_ {p, 0} &=&\ frac {f _ {\ mathrm {d}}} {\ sqrt {\ left (\ omega_ {0} ^ {2} - \ omega ^ {2} \ right) ^ {2} + \ gamma ^ {2} \ omega ^ {2}}}, \ end {array} $$ (6) $$ \ begin {array} {@ {} rcl @ {}} \ delta &=&\ tan ^ {- 1} \ frac {\ gamma \ omega} {\ omega_ {0} ^ {2} - \ omega ^ {2}}. \ end {array} $$ (7)
A solução clássica no espaço momentum é dada de forma semelhante, onde a função complementar é \ (P_ {c} (t) =me ^ {\ gamma t} \ dot {X} _ {c} (t) \) e a solução particular é \ (P_ {p} (t) =me ^ {\ gamma t} \ dot {X} _ {p} (t) \). Para investigar a fase geométrica do sistema, primeiro precisamos derivar soluções quânticas. Observe que o hamiltoniano do sistema dado na Eq. (3) é explicitamente dependente do tempo. Para derivar soluções quânticas do sistema, usamos o método do operador invariante [30, 31], que é um método útil quando tratamos tal sistema variável no tempo. Um operador invariante \ (\ hat {I} \) do sistema pode ser derivado da equação de Liouville-von Neumann, que é dada por \ ({d \ hat {I}} / {dt} ={\ partial \ hat {I}} / {\ partial t} + \ left [\ hat {I}, \ hat {H} \ right] / \ left (i \ hbar \ right) =0 \). Portanto, a partir de uma avaliação rigorosa após inserir a Eq. (3) nesta equação, temos um operador invariante linear [34] da forma
$$ \ hat {I} =\ hat {A} e ^ {i \ Omega t}, $$ (8)
onde \ (\ hat {A} \) é o operador de aniquilação que é dado por
$$ \ begin {alinhados} \ hat {A} =&\ left (2 \ hbar m \ Omega \ right) ^ {- 1/2} \ left [m \ left (\ Omega + i \ frac {\ gamma} { 2} \ right) e ^ {\ gamma t / 2} \ left [\ hat {x} -X_ {p} (t) \ right] \ right. \\ &\ left. + Ie ^ {- \ gamma t / 2} \ left [\ hat {p} -P_ {p} (t) \ right] \! {\ vphantom {\ left (\ Omega + i \ frac {\ gamma} {2} \ right)}} \ right]. \ end {alinhado} $$ (9)
O adjunto hermitiano da Eq. (9), \ (\ hat {A} ^ {\ dagger} \), é o operador de criação.

Podemos expressar a equação de autovalor de \ (\ hat {A} \) como
$$ \ hat {A} | A \ rangle =A | A \ rangle. $$ (10)
Ao avaliar a equação acima, temos a expressão do autovalor tal que
$$ A (t) =A (0) e ^ {- i \ Omega t}, $$ (11)
onde A (0) = A ₀ e ^{- i φ} com
$$ A_ {0} =\ left [m \ Omega / (2 \ hbar) \ right] ^ {1/2} X_ {c, 0}. $$ (12)
Enquanto o estado coerente | A 〉 É o estado próprio de \ (\ hat {A} \), o estado comprimido é o estado próprio de um operador \ (\ hat {B} \) que é dado por
$$ \ hat {B} =\ mu \ hat {A} + \ nu \ hat {A} ^ {\ dagger}, $$ (13)
onde μ e ν são variáveis complexas que geram a equação
$$ | \ mu | ^ {2} - | \ nu | ^ {2} =1. $$ (14)
Se escrevermos a equação de autovalor de \ (\ hat {B} \) na forma
$$ \ hat {B} | B \ rangle =B | B \ rangle, $$ (15)
| B 〉 É o estado comprimido. Ao resolver esta equação no espaço de configuração, temos
$$ {\ begin {align} \ langle {x} | B \ rangle =&^ {4} \! \! \! \ sqrt {\ frac {m \ Omega e ^ {\ gamma t}} {\ hbar \ pi (\ mu- \ nu) (\ mu ^ {*} - \ nu ^ {*})}} \ exp \ left \ {- \ frac {1} {\ hbar (\ mu- \ nu)} \ left [\ frac {1} {2} me ^ {\ gamma t} \ left ({\ vphantom {\ frac {1} {2}}} (\ mu + \ nu) \ Omega \ right. \ right. \ right. \\ &\ left. + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right) \ left [x-X_ {p} (t) \ right] ^ {2} - [iP_ { p} (t) (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \\ &\ left. \ left. \ times (\ mu A + \ nu A ^ {*})] \ left [x-X_ {p} (t) \ right] {\ vphantom {\ frac {1} {2} me ^ {\ gamma t}}} \ right] - \ frac {| A | ^ {2} + A ^ {2}} {2 (\ mu- \ nu) (\ mu ^ {*} - \ nu ^ {*})} \direito\}. \ end {alinhado}} $$ (16)
Assim, a função de onda no estado compactado foi derivada conforme fornecido na Eq. (16). As características quânticas do sistema podem ser esclarecidas com base nessa descrição analítica da função de onda. Para μ =1 e ν =0, Eq. (16) se reduz à função de onda no estado coerente, que é o autoestado da Eq. (10) no espaço de configuração. A função de onda, Eq. (16), será usado na próxima seção a fim de derivar a fase geométrica no estado comprimido.

Resultados e discussão

É bem sabido que a fase na evolução da onda quântica envolve tanto a fase geométrica quanto a fase dinâmica. A fase geométrica foi descoberta por Berry em 1984 [12] para um sistema que evolui ciclicamente com uma mudança adiabática. De acordo com o teorema adiabático da mecânica quântica, um autoestado instantâneo de um estado quântico em uma evolução cíclica no espaço de parâmetros permanecerá no mesmo estado mais tarde, enquanto há um acúmulo adicional da fase quântica que é a fase de Berry. Uma generalização da fase de Berry de uma forma que inclua a evolução não-adiabática, não cíclica e / ou não unitária do sistema quântico é a fase geométrica.

A fase geométrica no estado comprimido é dada por
$$ \ gamma_ {G} (t) =\ int_ {0} ^ {t} \ langle B (t ') | i \ frac {\ partial} {\ partial t'} | B (t ') \ rangle dt' + \ gamma_ {G} (0). $$ (17)
A diferenciação da função de onda em relação ao tempo no espaço de configuração torna-se
$$ \ frac {\ partial \ langle {x} | B \ rangle} {\ partial t} \, =\, \ left \ {f_ {1} (t) \! \ left [x-X_ {p} ( t) \ direita] ^ {2} \, + \, f_ {2} (t) \ esquerda [x \, - \, X_ {p} (t) \ direita] \, + \, f_ {3} ( t) \ right \} \! \! \ langle {x} | B \ rangle, $$ (18)
Onde
$$ f_ {1} (t) =- \ frac {m \ gamma e ^ {\ gamma t}} {2 \ hbar (\ mu- \ nu)} \ left ((\ mu + \ nu) \ Omega + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right), $$ (19) $$ {\ begin {alinhados} f_ {2} (t) &=\ frac {1} {\ hbar (\ mu- \ nu)} \ left [\ left ((\ mu + \ nu) \ Omega + \ frac {i \ gamma} {2} (\ mu- \ nu) \ right) P_ {p} (t) -ime ^ {\ gamma t} \ right. \\ &\ quad \ times \ left [\ omega_ {0} ^ {2} X_ {p} (t) - f _ {\ mathrm {d}} \ cos (\ omega t) \ right] (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \\ &\ quad \ left. \ times \ esquerda (\ frac {\ gamma} {2} \ esquerda (\ mu A + \ nu A ^ {*} \ direita) -i \ Omega \ esquerda (\ mu A - \ nu A ^ {*} \ direita) \ direita) \ direita], \\ \ end {alinhados}} $$ (20) $$ {\ begin {alinhados} f_ {3} (t) &\! =\ frac {\ gamma} {4} - \ frac {1} {\ hbar me ^ {\ gamma t} (\ mu- \ nu)} \ left [iP_ {p} (t) (\ mu- \ nu) + \ left (2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2} \ right. \\ &\ quad \ left. \ times \ left (\ mu A + \ nu A ^ {*} \ right) {\ vphantom {\ left ( 2 \ hbar m \ Omega e ^ {\ gamma t} \ right) ^ {1/2}}} \ right] P_ {p} (t) + \ frac {i \ Omega A ^ {2}} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}. \ end {alinhado}} $$ (21)
Avaliação adicional após inserir a Eq. (18) na Eq. (17) dá
$$ {\ begin {alinhados} \ gamma_ {G} (t) =&\ int_ {0} ^ {t} dt '\ left [A_ {0} ^ {2} \ left (\ frac {\ gamma ^ { 2}} {4 \ Omega} + \ Omega + g_ {1} \ sin \ left [2 \ left (\ Omega t '+ \ varphi \ right) \ right] + g_ {2} \ cos \ left [2 \ esquerda (\ Omega t '+ \ varphi \ direita) \ direita] \ direita) \ direita. \\ &\ esquerda.-A_ {0} \ esquerda [g_ {3} (t') \ sin \ esquerda (\ Omega t '+ \ varphi \ right) + g_ {4} (t') \ cos \ left (\ Omega t '+ \ varphi \ right) \ right] + g_ {5} (t') {\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] + \ gamma_ {G} (0), \ end {alinhado}} $$ (22)
Onde
$$ \ begin {array} {* {20} l} g_ {1} ~ &=\ frac {\ gamma} {2} + \ frac {i \ Omega \ left (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ right)} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}, \ end {array} $$ (23) $$ \ begin {array} {* {20} l} g_ {2} ~ &=\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ frac {2 | \ nu | ^ {2 } - \ left (\ mu \ nu ^ {*} + \ mu ^ {*} \ nu \ right)} {(\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)}, \ end {array} $$ (24) $$ \ begin {array} {* {20} l} g_ {3} (t) &=\ left (\ frac {2 \ Omega} {m \ hbar e ^ {\ gamma t}} \ right) ^ {1/2} P_ {p} (t), \ end {array} $$ (25) $$ {\ begin {alinhados} g_ {4} ( t) =\ frac {1} {\ sqrt {2 \ hbar \ Omega}} \ left (\ frac {\ gamma} {\ sqrt {me ^ {\ gamma t}}} P_ {p} (t) - 2 \ sqrt {me ^ {\ gamma t}} \ left [\ omega_ {0} ^ {2} X_ {p} (t) - f _ {\ mathrm {d}} \ cos (\ omega t) \ right] \ direita), \ end {alinhados}} $$ (26) $$ {\ begin {alinhados} g_ {5} (t) &=\ frac {P_ {p} ^ {2} (t)} {\ hbar mim ^ {\ gamma t}} + \ frac {\ gamma ^ {2}} {8 \ Omega} \ left [2 | \ nu | ^ {2} - \ left (\ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right) +1 \ right] \\ &\ quad + \ frac {i \ gamma} {4 (\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {* } \ right)} \ left [| \ mu | ^ {2} \ left (\ nu ^ {2} - \ nu ^ {* 2} \ right) - | \ nu | ^ {2} \ lef t (\ mu ^ {2} - \ mu ^ {* 2} \ direita) \ direita. \\ &\ quad \ esquerda. + (2 | \ nu | ^ {2} +1) \ esquerda (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ direita) + (\ mu- \ mu ^ {*}) (\ nu- \ nu ^ {*}) \ direita]. \ end {alinhado}} $$ (27)
O último termo em g ₅ que contém ( μ - μ ^∗ ) ( ν - ν ^∗ ) é uma fase inadequada porque é um número puramente imaginário. Portanto, agora removemos esse termo escolhendo pelo menos um de μ e ν como um valor real. Este remédio sempre pode ser feito sem perda de generalidade, pois apenas a fase relativa entre μ e ν tem significado físico em vez de suas fases absolutas.

A partir da execução da integração na Eq. (22), temos
$$ {\ begin {alinhados} \ gamma_ {G} (t) &=A_ {0} ^ {2} \ left [\ left (\ frac {\ gamma ^ {2}} {4 \ Omega} + \ Omega \ right) t + \ frac {g_ {1}} {\ Omega} \ sin (\ Omega t + 2 \ varphi) \ sin (\ Omega t) + \ frac {g_ {2}} {\ Omega} \ cos (\ Omega t + 2 \ varphi) \ right. \\ &\ quad \ left. \ Times \ sin (\ Omega t) {\ vphantom {\ frac {\ gamma ^ {2}} {4 \ Omega}}} \ right] \! - A_ {0} \ left [\ left (\ frac {2m \ Omega} {\ hbar} \ right) ^ {1/2} \ omega X_ {p, 0} \ bar {g} _ {3} (t) + \ sqrt {\ frac {2m} {\ hbar \ Omega}} \ frac {1} {4 \ omega ^ {2} + \ gamma ^ {2}} \ bar {g} _ { 4} (t) \ direita] \\ &\ quad + \ bar {g} _ {5} (t) + \ gamma_ {G} (0), \ end {alinhado}} $$ (28)
onde \ (\ bar {g} _ {i} (t) ~ (i =3,4,5) \) são dados por
$$ \ bar {g} _ {i} (t) =G_ {i} (t) -G_ {i} (0), $$ (29)
com
$$ {\ begin {alinhados} G_ {3} (\ tau) &=e ^ {\ gamma \ tau / 2} \ left (\ frac {1} {4 (\ Omega + \ omega) ^ {2} + \ gama ^ {2}} \ left \ {2 (\ Omega + \ omega) \ sin [(\ Omega + \ omega) \ tau + \ varphi- \ delta] \ right. \ right. \\ &\ quad \ left. + \ gamma \ cos [(\ Omega + \ omega) \ tau + \ varphi- \ delta] \ right \} - \ frac {1} {4 (\ Omega- \ omega) ^ {2} + \ gamma ^ {2}} \ {2 (\ Omega- \ omega) \\ &\ quad \ left. \ Left. \ Times \ sin [(\ Omega- \ omega) \ tau \, + \, \ varphi \, + \, \ delta] \ ! + \ gamma \ cos [(\ Omega- \ omega) \ tau \, + \, \ varphi \, + \, \ delta] \ right \} {\ vphantom {\ frac {1} {4 (\ Omega + \ ômega) ^ {2} + \ gamma ^ {2}}}} \ direita), \\ \ end {alinhado}} $$ (30) $$ {\ begin {alinhado} G_ {4} (\ tau) &=e ^ {\ gamma \ tau / 2} \ left \ {X_ {p, 0} \ left \ {\ gamma \ omega [2 \ omega \ cos (\ omega \ tau- \ delta) - \ gamma \ sin ( \ omega \ tau- \ delta)] -2 \ omega_ {0} ^ {2} \ right. \ right. \\ &\ quad \ left. \ times [2 \ omega \ sin (\ omega \ tau- \ delta ) + \ gamma \ cos (\ omega \ tau- \ delta)] {\ vphantom {X_ {p, 0}}} \ right \} + 2f _ {\ mathrm {d}} [2 \ omega \ sin (\ omega \ tau) \\ &\ left. \ left. \ quad + \ gamma \ cos (\ omega \ tau) \ right] {\ vphantom {X_ {p, 0}}} \ right \}, \\ \ end {alinhado }} $$ ( 31) $$ {\ begin {alinhados} G_ {5} (\ tau) &=\ frac {m \ omega ^ {2}} {2 \ hbar} X_ {p, 0} ^ {2} \ frac {e ^ {\ gamma \ tau}} {\ gamma \ left (4 \ omega ^ {2} + \ gamma ^ {2} \ right)} \ left \ {\ gamma ^ {2} +4 \ omega ^ {2} - \ gamma ^ {2} \ cos [2 (\ omega \ tau - \ delta)] \ right. \\ &\ quad \ left.-2 \ gamma \ omega \ sin [2 (\ omega \ tau - \ delta )] {\ vphantom {\ gamma ^ {2} +4 \ omega ^ {2} - \ gamma ^ {2}}} \ right \} + \ frac {\ gamma ^ {2} \ tau} {8 \ Omega } \ left [2 | \ nu | ^ {2} - \ left (\ mu \ nu + \ mu ^ {*} \ nu ^ {*} \ right) +1 \ right] \\ &\ quad + \ frac {i \ gamma \ tau} {4 (\ mu- \ nu) \ left (\ mu ^ {*} - \ nu ^ {*} \ right)} \ left [| \ mu | ^ {2} \ left (\ nu ^ {2} - \ nu ^ {* 2} \ right) - | \ nu | ^ {2} \ left (\ mu ^ {2} - \ mu ^ {* 2} \ right) \ right. \\ &\ quad \ left. + \ left (2 | \ nu | ^ {2} +1 \ right) \ left (\ mu \ nu ^ {*} - \ mu ^ {*} \ nu \ right) \ right]. \ end {alinhado}} $$ (32)
Assim, avaliamos a fase geométrica completa no estado comprimido, que é dado pela Eq. (28) com Eqs. (23), (24) e (29) - (32).

A evolução temporal da fase geométrica foi ilustrada nas Figs. 1, 2, 3 e 4. Na Fig. 1, vemos que a fase geométrica oscila e o envelope de tal oscilação aumenta com o tempo. O aumento do envelope é maior quando A ₀ é grande. O padrão de oscilação torna-se gradualmente irregular conforme os valores de μ e ν aumentar. Além disso, a amplitude da oscilação torna-se grande com o passar do tempo.

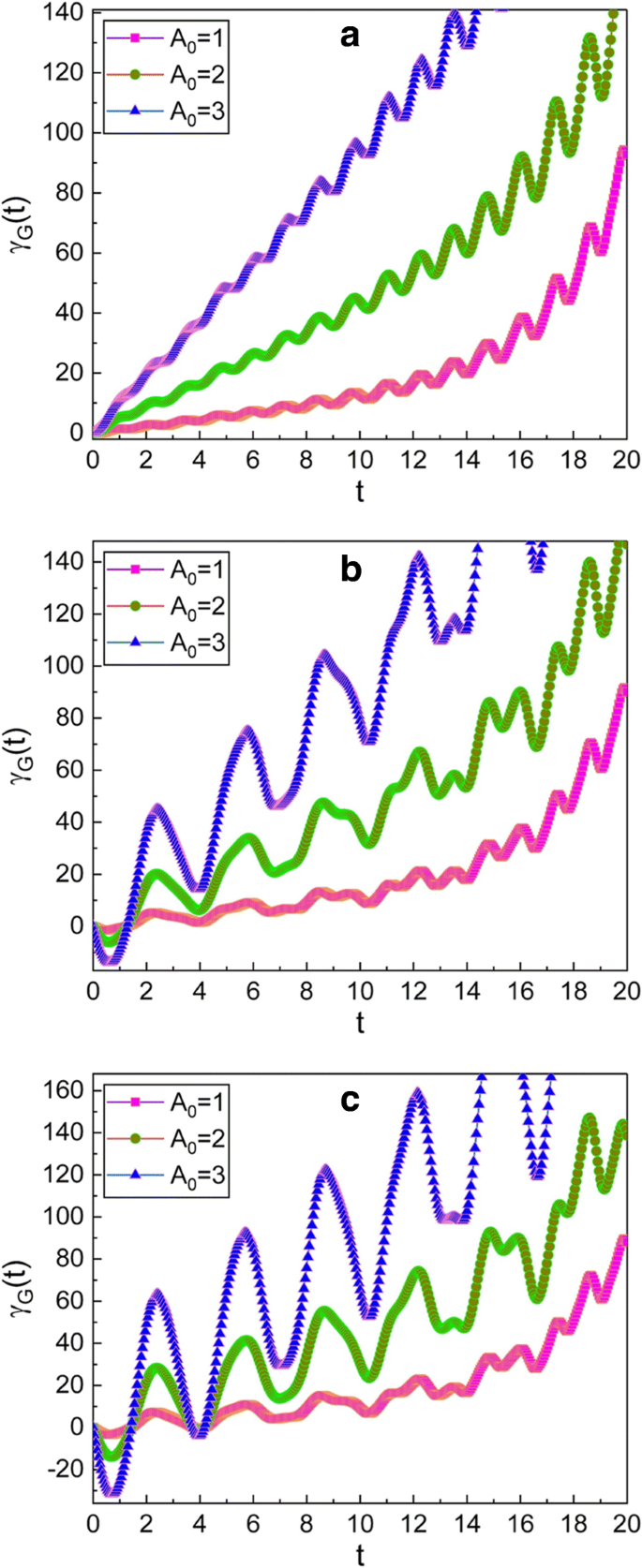
Evolução temporal da fase geométrica para vários valores diferentes de A ₀ . Os valores de ( μ , ν ) usados nos gráficos são (1, 0) para a , (\ (\ sqrt {2} \), 1) para b , e (\ (\ sqrt {3} \), \ (\ sqrt {2} \)) para c . Usamos m =1, ω ₀ =1, ω =5, γ =0,35, f _d =1, \ (\ hbar =1 \), φ =0, e γ _G (0) =0. A fase e todos os parâmetros são considerados adimensionais por conveniência, e essa convenção também será aplicada às figuras subsequentes. Porque A ₀ é dado em termos da amplitude clássica X _{c , 0} da função complementar [ver Eq. (12)], podemos confirmar pelos gráficos que a fase geométrica é grande quando a amplitude de oscilação é alta. Também vemos que a flutuação de γ _G ( t ) torna-se grande à medida que os valores μ e ν aumentar sob a condição dada na Eq. (14)

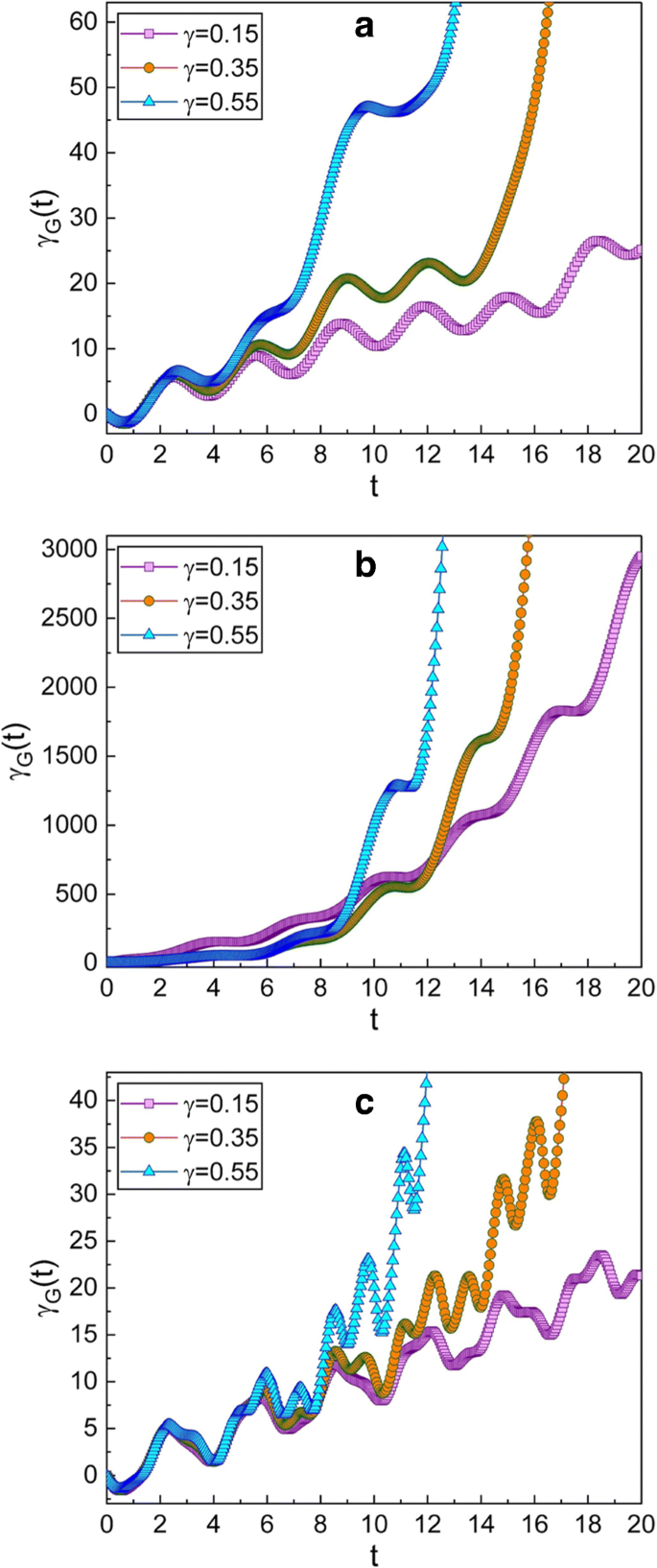
Evolução temporal da fase geométrica para vários valores diferentes de γ . O valor de ω usado nos gráficos é 0,3 para a , 0,99 para b e 5 para c . Os parâmetros de compressão escolhidos aqui são \ (\ mu =\ sqrt {2} \) e ν =1; esta escolha dá q - estado pressionado no momento inicial. Outras quantidades que usamos são m =1, ω ₀ =1, A ₀ =1, f _d =1, \ (\ hbar =1 \), φ =0, e γ _G (0) =0. Confirmamos que a fase geométrica é grande quando o fator de amortecimento γ é grande na maioria dos casos, mas não em todos. A frequência do caso b está perto da frequência de ressonância, enquanto os de a e c estão longe de ser ressonantes. A fase geométrica para o caso ressonante ( b ) aumenta muito rapidamente com o tempo

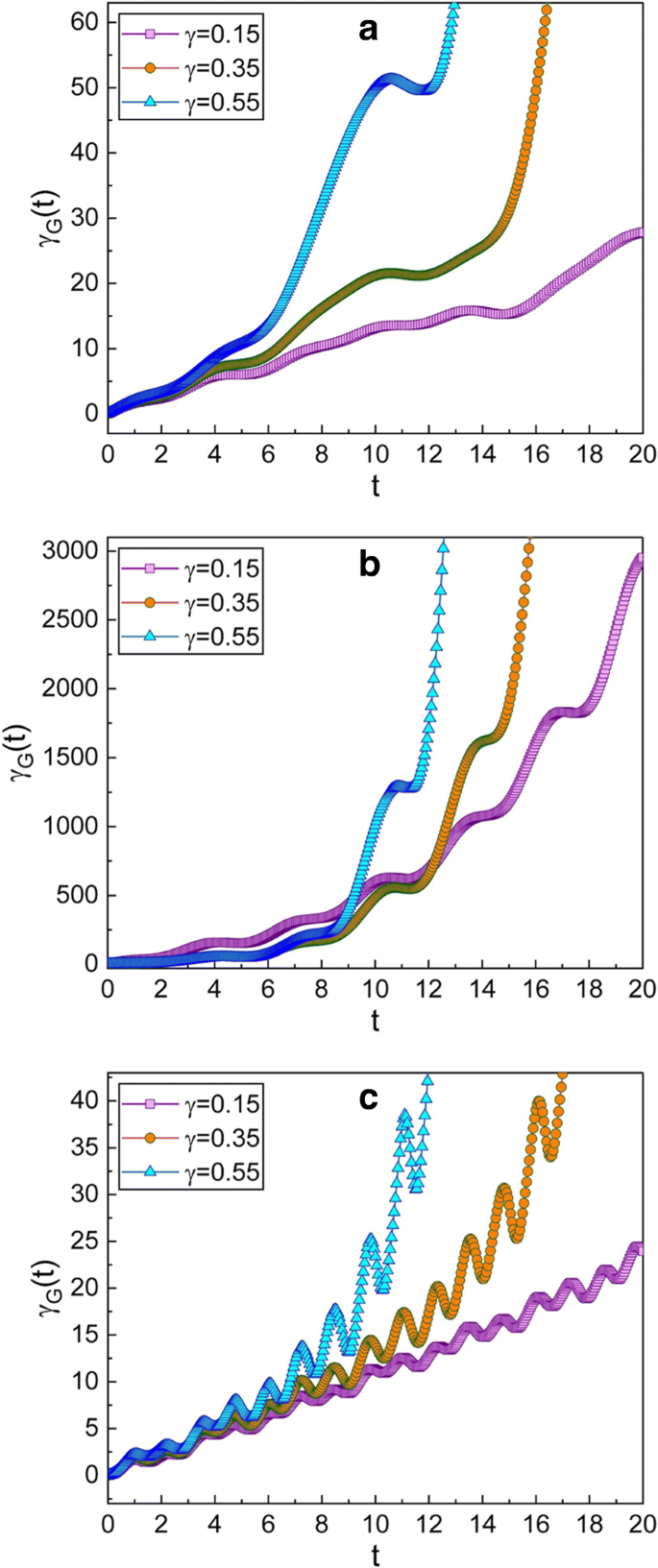
a - c Este gráfico é igual ao da Fig. 2, mas para o caso em que os parâmetros de compressão escolhidos são \ (\ mu =\ sqrt {2} \) e ν =−1 que dá um p - estado pressionado no momento inicial. Pelo fato de que os gráficos gerais neste caso não são muito diferentes dos correspondentes da Fig. 2, podemos confirmar que a evolução de γ _G ( t ) é quase irrelevante para os tipos de compressão, desde que os valores absolutos de μ e ν não mude

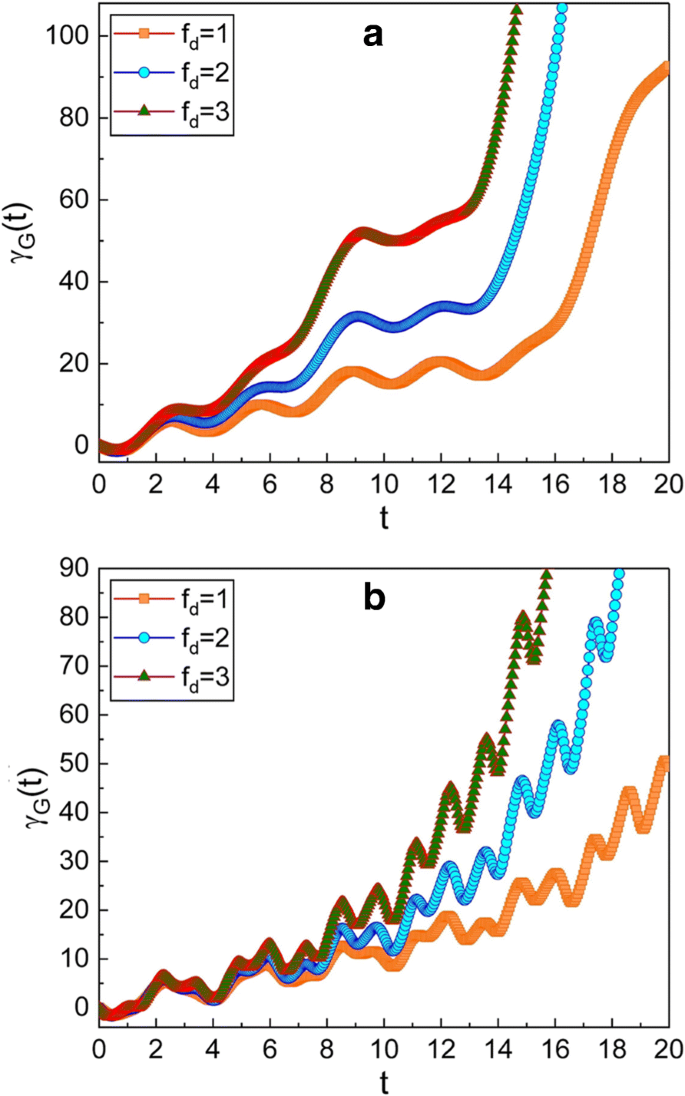
Evolução temporal da fase geométrica para vários valores diferentes de f _d . O valor de ω usado nos gráficos é 0,3 para a e 5 para b . Usamos \ (\ mu =\ sqrt {2} \), ν =1, m =1, ω ₀ =1, γ =0,3, A ₀ =1, \ (\ hbar =1 \), φ =0, e γ _G (0) =0. Como a amplitude ( f _d ) do aumento da força motriz, a fase geométrica torna-se grande

Os efeitos de compressão no estado comprimido dependendo do parâmetro de compressão c onde c = μ / ν foi investigado na ref. [39]. De acordo com a análise dada na ref. [39] (ver Fig. 1 (a) na ref. [39]), o estado comprimido ilustrado na Fig. 2, que corresponde a \ (c =\ sqrt {2} \), é o q -estado pressionado no momento inicial, enquanto o da Fig. 3, que corresponde a \ (c =- \ sqrt {2} \), é o p -estado pressionado na mesma situação. Ao comparar as Figs. 2 e 3 entre si, podemos concluir que a fase geométrica no q -estado pressionado é quase o mesmo que no p -estado pressionado.

Os efeitos de γ sobre a evolução da fase geométrica pode ser confirmada pelas Figs. 2 e 3. A fase geométrica aumenta mais rapidamente quando γ é grande. Ao comparar as Figs. 2a e 3a com as Figs. 2c e 3c, podemos confirmar que a fase geométrica varia um tanto rapidamente quando ω é maior do que a frequência angular de ressonância.

O comportamento temporal da fase geométrica no ou próximo ao estado ressonante do sistema pode ser de grande interesse [22, 23]. As Figuras 2b e 3b mostram que a fase geométrica aumenta muito rapidamente quando ω está perto da frequência angular de ressonância. Isso significa que a função de onda nesta situação varia significativamente ao longo do tempo, pois a magnitude da fase geométrica está relacionada à variação do tempo da função de onda. Na verdade, a amplitude da oscilação do fio é notavelmente aumentada no estado de ressonância. A propósito, as frequências angulares de ressonância de ressonadores de nanofios baseados em CNT em suspensão não são apenas altas, mas também amplamente sintonizáveis com fatores de qualidade muito alta [3]. Por este motivo, os modos vibracionais do sistema serão mantidos por um longo tempo até que sejam totalmente amortecidos [11].

A Figura 4 mostra que a fase geométrica também é afetada pela amplitude da força motriz f _d . Como f _d aumenta, o incremento da fase geométrica no tempo é rápido.

Conclusão

Investigamos a fase geométrica no estado comprimido para o sistema com base na dinâmica quântica com a equação de Schrödinger. Em relação à dependência temporal do hamiltoniano que descreve o sistema, foi introduzido o método do operador invariante, que é uma ferramenta potencial para derivar soluções quânticas no caso em que o hamiltoniano é descrito em termos de tempo. Por meio deste método, a fórmula analítica da fase geométrica para a oscilação do nanofio à base de CNT foi obtida.

Foi realizada uma análise detalhada dos efeitos de fase, necessária para uma compreensão teórica das vibrações mecânicas. Nosso desenvolvimento da fase geométrica é totalmente baseado em quantum, com avaliações matemáticas rigorosas. A fase geométrica é sensível à mudança dos parâmetros mecânicos e apresenta oscilação em um grande número de casos. A influência dos parâmetros de compressão na evolução da fase geométrica também foi analisada. Confirmamos um forte aumento da acumulação de fase geométrica ao longo do tempo perto da frequência angular ressonante.

Nossos resultados ilustram o comportamento temporal da fase geométrica que aparece na vibração de um nanofio à base de CNT. A análise da fase geométrica dada neste trabalho é importante para a compreensão não apenas das características topológicas do sistema, mas também das vibrações dinâmicas de outros osciladores mecânicos baseados em nanofios. Em particular, desenvolvemos propriedades de fase do estado ressonante, cujo esclarecimento é necessário na aplicação do sistema em tecnologias de informação quântica e outras indústrias de base quântica [40]. O método e estrutura semelhantes usados nesta pesquisa também podem ser estendidos a outros nano sistemas, como ressonadores supercondutores Fabry-Perot [41], nano cantiléveres [42] e sistemas híbridos qubit-ressonador-átomo [43].

Abreviações

CNT:: Nanotubo de carbono
Ondas EM:: Ondas eletromagnéticas
TDHS:: Sistema hamiltoniano dependente do tempo

Crescimento direto de nanofios de GaN cristalino único em sílica revestida com óxido de estanho de índio FETs de canal U de porta retangular de alto desempenho com distância de apenas 2 nm entre os contatos de origem e drenagem

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias