Absorção perfeita induzida por plasma no sistema de grafeno / metal

Resumo

A interferência construtiva dos modos plasmônico claro e escuro resulta no efeito de absorção induzida pelo plasmon (PIA). Aqui, investigamos teoricamente o efeito PIA, que é realizado pela interferência construtiva entre um modo de ressonância Fabry-Perot (F-P) e um modo quase guiado de grafeno. A simulação numérica revela pelo menos três vantagens de nossa estrutura em relação às anteriores. Primeiro, a taxa de extinção pode chegar a ~ 99,999%, resultando em uma figura de mérito ultra-alta * (FOM *) tão alta quanto 10 ⁶ . Em segundo lugar, a intensidade desse efeito PIA pronunciado pode ser otimizada ajustando a distância de acoplamento. Terceiro, a frequência de ressonância pode ser facilmente sintonizada ajustando o nível de Fermi do grafeno. Este sistema pode ter aplicações potenciais em comutação óptica dinâmica e detecção bioquímica.

Histórico

A plasmônica tem atraído grande atenção devido às suas propriedades extraordinárias [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] e enorme potencial em muitos campos, incluindo o integrado fotônica, bio-sensoriamento, captura de energia, fotodetecção. Recentemente, um novo fenômeno plasmônico, conhecido como spoof surface plasmons (SSPs), foi observado, o qual pode se propagar através de metais perfurados e superar o limite de difração [16]. SSPs foram então explorados no THz, micro-ondas e faixa de frequência inferior [17,18,19], e uma série de dispositivos de sub-onda profundo baseados em SSPs foram demonstrados [20, 21]. No entanto, a aplicação de tais dispositivos é seriamente prejudicada pela alta taxa de amortecimento dos SPPs. Uma solução para esse problema é o meio de transparência induzida por plasmon artificial (PIT) [22], que apresenta uma janela de transparência nítida dentro de um amplo espectro de absorção. O efeito PIT depende principalmente do acoplamento de um elemento radiativo e um elemento sub-radiante, que tem sido amplamente estudado [23,24,25]. Um fenômeno semelhante, absorção induzida por plasmon (PIA), também foi demonstrado recentemente, que resulta da interferência construtiva de modos plasmônicos claros e escuros [26]. A ressonância PIA [27, 28] pode exibir um notável efeito de luz rápida, que tem aplicações potenciais em comutação e processamento óptico.

Porém, os dispositivos tradicionais baseados no efeito PIA da estrutura metálica são difíceis ou impossíveis de obter sintonia, o que restringe seriamente suas aplicações. O grafeno [29, 30], conhecido por sua semimetalicidade, alta mobilidade e alta capacidade de ajuste, pode ser um excelente material candidato para dispositivos plasmônicos infravermelhos sintonizáveis. Neste artigo, investigamos um efeito PIA ajustável, que é obtido pela interferência construtiva de um modo de ressonância F-P e um modo quase-guiado suportado por um sulco de prata periódico e grafeno monocamada, respectivamente. Verificou-se que a força da ressonância e a largura da linha são fortemente dependentes da distância de acoplamento. Também é mostrado que a taxa de extinção pode chegar a ~ 99,999%. A taxa de extinção é definida como 1- R - T , onde R e T são a refletância e a transmitância, respectivamente. É simplesmente 1- R em nosso sistema, uma vez que a transmitância aqui é 0. Como resultado, um FOM * ultra-alto tão alto quanto 10 ⁶ no sistema de grafeno / metal pode ser alcançado e a frequência de ressonância pode ser dinamicamente sintonizável ajustando a tensão de porta do grafeno. Essas propriedades proeminentes podem ser aplicadas em detecção bioquímica e comutação óptica dinamicamente.

Métodos

O esquema de nossa estrutura é mostrado na Fig. 1, consistindo em uma monocamada de grafeno e um Al ₂ O ₃ camada isolada no topo de uma prata ranhurada. A espessura do Al ₂ O ₃ é g . O sistema é iluminado por uma onda plana incidente normal de polarização magnética transversal (TM). Os outros parâmetros estruturais são expressos da seguinte forma: d é a profundidade da ranhura de prata; w é a largura da ranhura de prata; P é o período da célula unitária. Na região do infravermelho médio, o espalhamento intrabanda domina no grafeno altamente dopado e sua condutividade assume a forma de Drude σ _g = ie ² E _F / [ πħ ² ( ω + iτ ^-1 )]. O tempo de relaxamento do elétron é expresso como τ = μE _F / eυ _F ² , onde υ _F = c / 300 é a velocidade de Fermi, E _F é a energia Fermi e μ =10 m ² / Vs é a mobilidade DC do grafeno [25, 31, 32]. Nas simulações de domínio de tempo de diferença finita (FDTD), as constantes ópticas para prata e Al ₂ O ₃ são da ref. [33] e ref. [34]. As condições de contorno periódicas são usadas para simular estruturas celulares periódicas infinitas. Para simplificar, assumimos que o material da região acima da camada de grafeno é o vácuo ( ε ₀ =1).

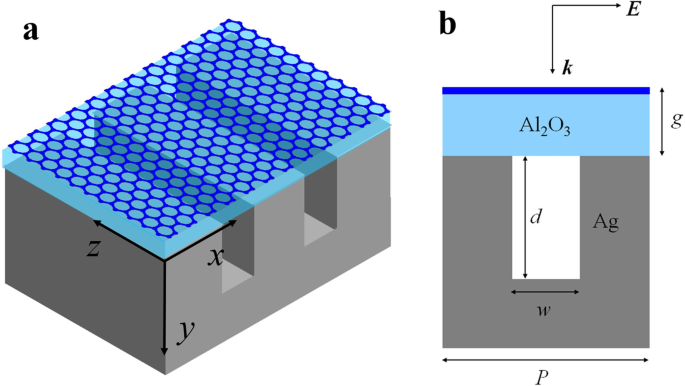
Diagrama esquemático da estrutura do sulco de grafeno-prata. a Visão oblíqua. b O diagrama de seção transversal de uma célula unitária

Resultados e discussão

Simulamos o espectro de reflexão da ranhura de prata com w =100 nm, P =250 nm, d =2000 nm, e o resultado é mostrado na Fig. 2a (curva vermelha). Uma grande queda pode ser observada em ~ 28 THz, com uma taxa de extinção de ~ 44% e Q fator ~ 0,8, que é devido a uma ressonância F-P induzida pelo SSP excitado pela luz incidente [19]. Esta ressonância tem uma ampla gama de bandas de ressonância e, portanto, o modo de ressonância pode servir como o modo superradiante em nosso sistema PIA. Em seguida, calculamos o espectro de reflexão da folha de grafeno com condições de contorno de metal na parte inferior da área de simulação, com um nível de Fermi E _F =0,3 eV, conforme mostrado na Fig. 2a (curva azul). O espectro de reflexão mostra que a ressonância do plasmão grafeno não pode ser excitada diretamente pela incidência nesta frequência. Para visualizar e otimizar o modo plasmon suportado pelo grafeno, primeiro simulamos os modos de ressonância suportados pelo grafeno. Para eliminar o impacto potencial da ressonância F-P da ranhura de prata, assumimos que a ranhura é feita de silício em vez de prata. Os espectros de refletância da estrutura foram calculados para E _F =0,3 eV e célula unitária diferente P e é mostrado na Fig. 2b. Uma queda de refletância na frequência de ressonância f =32,84 THz pode ser observado para P =250 nm com um Q fator ~ 304. O alto Q a ressonância com uma banda de ressonância estreita pode servir como o modo sub-radiante (escuro) em nosso sistema PIA. O mergulho de refletância é devido à ressonância do modo quase-guiado plasmônico no grafeno com a incidência normal [35], uma vez que a ranhura pode compensar a incompatibilidade do vetor de onda com base no m condição de combinação de fase de ordem [36, 37]

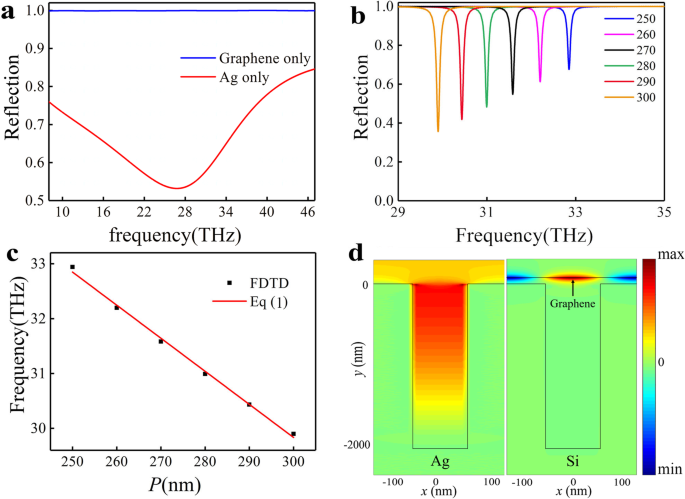
Resposta óptica dos modos individuais. a Os espectros de refletância da estrutura do sulco de prata apenas (linha vermelha) e apenas do grafeno (linha azul) em incidência normal, respectivamente. b Os espectros de refletância da estrutura do sulco de grafeno-Si para diferentes períodos P de célula unitária. c A modelagem numérica e os resultados analíticos da frequência de ressonância f , respectivamente. d O campo elétrico E _x distribuições de modo F-P (esquerda) e modo de ressonância quase guiada de grafeno (direita).
$$ {k} _0 \ operatorname {Re} \ left ({n} _ {\ mathrm {eff}} \ right) =\ left | {k} _x + {mG} _x \ right | ,, $$ (1)
onde k _x = k ₀ sin θ , k ₀ =2 π / λ é o vetor de onda no espaço livre, θ é o ângulo entre a luz incidente e y -direcção, n _eff é o índice de refração efetivo do modo de guia de onda TM no grafeno, e G _x é o vetor de rede recíproco da grade ( G _x =2 π / P ) Na discussão a seguir, o ângulo de luz incidente de y -direcção é zero ( θ =0 °). A situação para outros ângulos incidentes é discutida no arquivo adicional 1. As posições dessas quedas de refletância correspondem à frequência de ressonância do modo quase-guiado no grafeno, conforme mostrado na Fig. 2b. Os resultados da simulação concordam bem com a Eq. (1), onde m =1 e o índice de refração efetivo, ~ 33, é obtido por soluções de FDTD, como mostrado na Fig. 2c. O campo elétrico E _x distribuições de modo F-P e modo quase guiado de grafeno foram mostradas na Fig. 2d. Observa-se que o confinamento de energia dos modos SSP sustentado pela superfície ranhurada de Si pode ser insignificante em comparação com o modo quase guiado de grafeno.

Na situação de acoplamento, os dois modos próprios serão fortemente acoplados quando se aproximarem e, portanto, o espectro de reflexão será dramaticamente alterado. Um estreito mergulho de largura de sub-linha de absorvância aprimorada com uma razão de extinção de ~ 99,97% é observado no topo do mergulho de refletância mais amplo, como mostrado na Fig. 3a. Ao aumentar a distância vertical g , o acoplamento de campo próximo e o modo quase guiado se tornam mais fracos, conforme a modulação do mergulho de refletância se torna menor. Existem duas maneiras possíveis de fazer com que o mergulho da refletância seja menor, quais são o acoplamento mais fraco e a excitação do modo quase guiado mais fraco. Portanto, usamos o modelo de oscilador acoplado para entender quantitativamente o sistema PIA [38].
$$ \ left (\ begin {array} {c} {\ tilde {a}} _ 1 \\ {} {\ tilde {a}} _ 2 \ end {array} \ right) =- {\ left (\ begin { array} {cc} \ left (\ omega - {\ omega} _1 + \ frac {i {\ gamma} _1} {2} \ right) &\ tilde {\ kappa} \\ {} \ tilde {\ kappa} &\ left (\ omega - {\ omega} _2 + \ frac {i {\ gamma} _2} {2} \ right) \ end {array} \ right)} ^ {- 1} \ left (\ begin {array} { c} b {\ tilde {E}} _ 0 \\ {} 0 \ end {array} \ right) $$ (2)

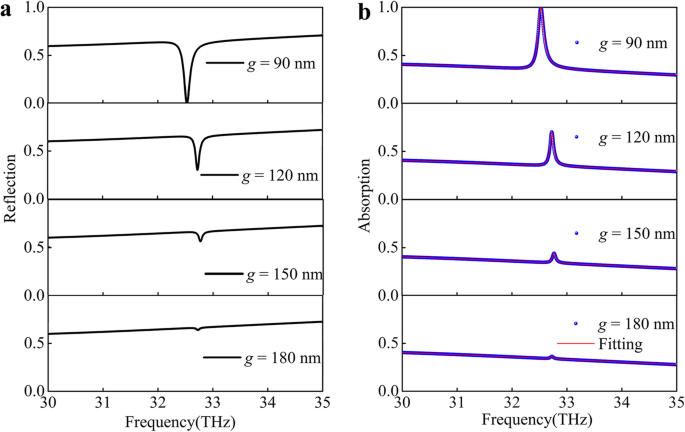
A resposta óptica varia com a distância de acoplamento. a A reflexão. b Espectros de absorção da estrutura do sulco de grafeno-prata em incidência normal para distâncias diferentes g entre o grafeno e o sulco de prata. A curva preta / as bolas azuis são calculadas pelo método FDTD e a curva vermelha é um ajuste analítico pela Eq. (3) do dispositivo PIA

Onde \ ({\ tilde {a}} _ {1,2} ={a} _ {1,2} \ left (\ omega \ right) {\ mathrm {e}} ^ {i \ omega t} \) , ω _1,2 e γ _1,2 são as amplitudes harmônicas de tempo, frequências ressonantes e constantes de amortecimento do modo claro e escuro, respectivamente. b é o coeficiente de acoplamento que mede o quão forte o modo brilhante se acopla ao campo elétrico incidente. \ (\ tilde {\ kappa} =\ kappa {e} ^ {i \ varphi} \) é um parâmetro de acoplamento complexo, que é introduzido para expressar o efeito de retardo de fase. φ é uma mudança de fase, que é um coeficiente chave para determinar a forma de interferência entre as duas vias coerentes. Quando φ =0 é um parâmetro real e o comportamento típico do efeito PIT pode ser observado, e a interferência entre as duas vias coerentes é destrutiva. Para φ =π / 2 é um parâmetro imaginário puro e a interferência entre as duas vias coerentes é convertida de destrutiva em construtiva [26]. A absorção do sistema pode ser calculada como a energia dissipada com base na fórmula (2), que é
$$ A \ left (\ omega \ right) =\ Im \ left (\ frac {b \ left (\ omega - {\ omega} _2 + \ frac {i {\ gamma} _2} {2} \ right)} { \ kappa ^ 2 {e} ^ {i2 \ varphi} - \ left (\ omega - {\ omega} _1 + \ frac {i {\ gamma} _1} {2} \ right) \ left (\ omega - {\ omega } _2 + \ frac {i {\ gamma} _2} {2} \ right)} \ right) $$ (3)
Em seguida, ajustamos os espectros de absorção numéricos com a Eq. (3) para g diferente , que foram mostrados na Fig. 3b (curvas vermelhas). Os resultados da simulação estão de acordo com os resultados da modelagem analítica baseada no modelo do oscilador acoplado, o que confirma fortemente o princípio de design do nosso dispositivo PIA. Os parâmetros de ajuste κ , φ , γ ₁ , e γ ₂ foram mostrados na Fig. 4a-c. O crescente g produz uma diminuição no parâmetro de acoplamento κ , como mostrado na Fig. 4a. Ao diminuir gradualmente o acoplamento (aumentando g ), a fase φ permanece inalterado, e γ ₂ diminui gradualmente enquanto γ ₁ mudanças ligeiramente mostradas na Fig. 4b, c. O parâmetro de acoplamento κ exceder as constantes de amortecimento do modo escuro γ ₂ para a distância mínima de lacuna, que confirma que o acoplamento do modo claro para o modo escuro é mais forte do que os processos de dissipação na folha de grafeno.

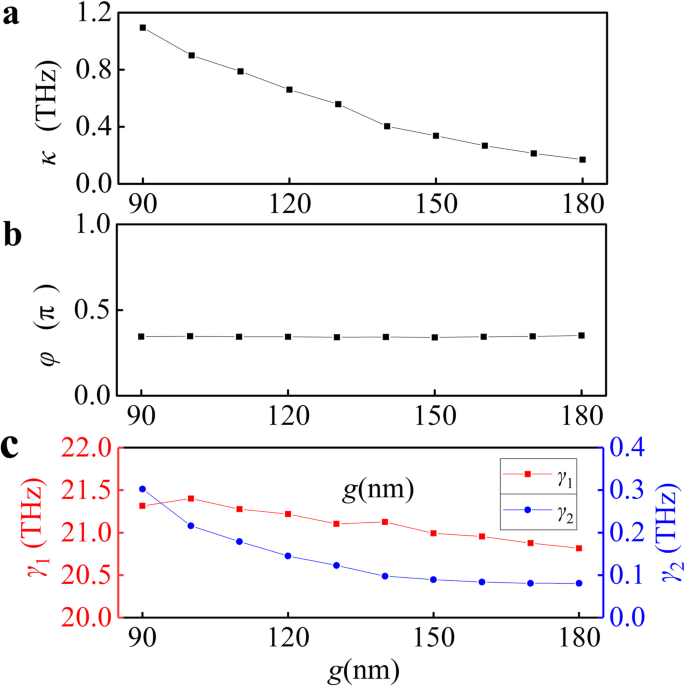
Análise quantitativa de respostas ópticas em sistemas acoplados. Numérico extraído ( a ) acoplamento, ( b ) fase, e ( c ) coeficientes de amortecimento em função da lacuna g . Valores de κ , φ , e γ ₁ , γ ₂ foram extraídos ajustando os espectros de absorção numéricos

Para visualizar a interferência construtiva entre os modos claro e escuro, investigamos a evolução do campo magnético da estrutura com o tempo, e dois H _z os monitores foram colocados a 3 nm de distância do centro do grafeno e a 1000 nm da parte inferior da ranhura de prata, respectivamente. A diferença de fase oscilante entre os dois modos é de 0,5π, conforme indicado na Fig. 5a. A distribuição do campo magnético em um tempo diferente foi calculada na frequência de ressonância PIA f _q =32,5 THz, onde ω _q t ₁ ~ 2,00 π e ω _q t ₂ ~ 2,50π, conforme indicado na Fig. 5b, c. O máximo do campo magnético no sulco de prata pode ser observado para 2,00π enquanto o campo magnético do grafeno atinge seu máximo para 2,50π, indicando o acoplamento fora de fase entre as duas estruturas. Portanto, a evolução e formação da ressonância são determinadas por interferência construtiva [39].

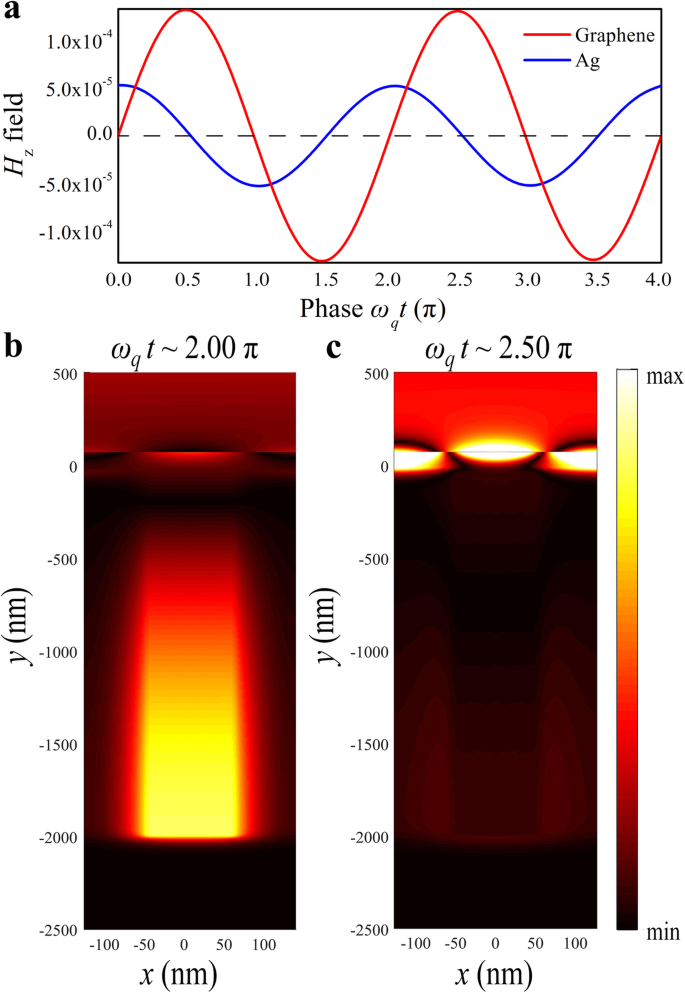
Evolução de modos acoplados no domínio do tempo. a Evolução do tempo calculada da força do campo magnético no grafeno (linha vermelha) e no sulco de prata (linha azul). Calculado z componente das distribuições do campo magnético para g =90 nm. A força máxima de campo no sulco de prata e grafeno são observados em tempos diferentes b ω _q t ₁ ~ 2,00π e c ω _q t ₂ ~ 2,50π, respectivamente

Na aplicação prática, uma faixa de reflexão estreita e uma alta taxa de extinção são altamente desejadas. Para atingir essas duas condições, podemos ajustar o período da unidade P e profundidade do sulco de prata d para otimizar nossos parâmetros estruturais. Depois de calcular o espectro de reflexão de diferentes parâmetros de estrutura P de 1900 a 2100 nm e d de 245 a 265 nm por FDTD, ganhamos uma taxa de extinção muito alta ~ 99,999% em P =254 nm e d =1980 nm. O espectro de refletância do dispositivo PIA sob diferentes ambientes de índice de refração é mostrado na Fig. 6a. As capacidades de detecção são definidas como [39]:
$$ {\ displaystyle \ begin {array} {c} S =\ Delta f (THz) / \ Delta n, FOM =S / FWHM \ (THz), \\ {} S \ ast =\ Delta I / \ Delta n, FOM \ ast =S \ ast / I, \ end {array}} $$ (4)

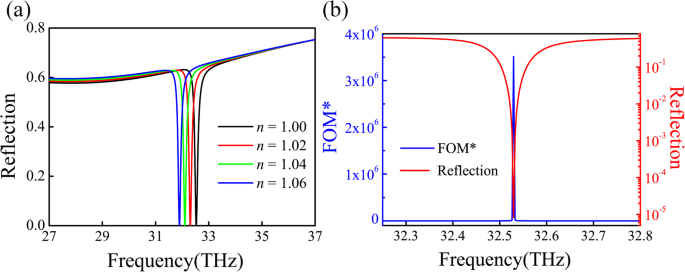
O desempenho de detecção do sistema. a A resposta de detecção do sensor PIA para ambiente dielétrico variado. b A curva FOM * relacionada e os espectros de refletância

onde f e eu são a frequência de ressonância e a intensidade espectral, respectivamente. Ao medir a intensidade de reflexão de um sensor, a capacidade de sensibilidade do sensor pode ser quantificada pelo valor FOM *. Quanto mais alto for o valor, maior será a sensibilidade do sensor. Da Fig. 6 a, podemos obter S =11,2 THz / RIU e o FOM associado ~ 94,1, com a largura total na metade do máximo (FWHM) ~ 30 nm (0,12 THz). Este FOM é maior do que o valor em absorvedores de metamateriais com base na ressonância da rede de superfície. Além disso, nosso sensor PIA pode levar a um valor FOM * ultra-alto 3,5 × 10 ⁶ , conforme indicado na Fig. 6b. Comparamos o desempenho dos sensores recentemente estudados no arquivo Adicional 1:Tabela S1.

No sistema PIA, o grafeno desempenha outro papel fundamental. A modulação da frequência ressonante pode ser alcançada ajustando a tensão de disparo para ajustar o nível de Fermi do grafeno. Os espectros simulados são mostrados nos arquivos adicionais 2:Figura S1 e 3:Figura S2. O controle ativo de mudança de frequência da ressonância PIA é significativo para o sensor ou absorvedor.

Conclusões

Em resumo, demonstramos numericamente a absorção perfeita induzida pela interferência construtiva entre o modo de ressonância F-P e o modo quase guiado de grafeno plasmônico. Através da introdução do modo quase guiado de grafeno plasmônico, obtemos a linha espectral com uma largura de linha mais estreita do modo de ressonância F-P do sulco de prata. Quando a distância g for aumentada gradualmente, a força da ressonância e a largura da linha diminuirão. Para o aplicativo, o FOM * em nosso sistema pode atingir 10 ⁶ . Além disso, a janela de absorção pode ser ajustada variando o parâmetro geométrico e o nível de Fermi do grafeno. Esses resultados podem fornecer um novo caminho para a realização do controle espectral dinâmico do infravermelho médio em nanoescala e sensores ópticos ultrassensíveis.

Disponibilidade de dados e materiais

Todos os dados gerados ou analisados durante este estudo estão incluídos neste artigo publicado [e seus arquivos de informações complementares].

Abreviações

FDTD:: Domínio do tempo de diferença finita
FOM *:: Figura de mérito*
F-P:: Fabry-Perot
FWHM:: Largura total pela metade no máximo
PIA:: Absorção induzida por plasma
PIT:: Transparência induzida por plasma
Q fator:: Fator de qualidade
SSPs:: Plasmões de superfície spoof
TM:: Magnético transversal

Produção de hidrogênio solar a partir de óxido estânico econômico sob irradiação de luz visível Propriedades eletrônicas e de transporte resolvidas por spin de nanojunções baseadas em Graphyne com diferentes posições de substituição de N

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias