Transformação de fase anisotrópica na liga de CuZr cristalino B2
Resumo
Partículas de cobre-zircônio de fase B2 (CuZr) são freqüentemente usadas como um agente de intensificação para melhorar a tenacidade do vidro metálico; no entanto, a dependência da orientação de seus comportamentos de transformação de fase sob carregamento permanece obscura. Neste trabalho, simulações por dinâmica molecular de tensão uniaxial e compressão da fase B2 CuZr ao longo de diferentes orientações cristalográficas são realizadas para investigar a resposta mecânica relacionada à orientação e os mecanismos de transformação de fase. Verificou-se que o comportamento mecânico do CuZr exibe uma assimetria de tensão / compressão óbvia, mas seu modo de falha é principalmente a amorfização local. Três diferentes comportamentos de transformação de fase, B2 → FCC, B2 → BCT e B2 → HCP, foram observados em tração e compressão ao longo de [001], e tensão ao longo de [110], respectivamente. As transformações são realizadas por rotação da rede (~ 5 °), deformação uniforme e separação entre as camadas atômicas de Cu e Zr, respectivamente. Antes da falha por amorfização local, a região de transformação de fase pode ser recuperada após o descarregamento, mostrando a superelasticidade.
Introdução
Os vidros metálicos a granel (BMGs) têm atraído considerável atenção devido às suas excelentes propriedades mecânicas e físicas, como alta resistência, elasticidade, alta dureza combinada com excelente resistência à corrosão, etc. [1,2,3,4]. No entanto, eles geralmente falham por fratura frágil catastrófica através de bandas de cisalhamento localizadas [5, 6]. Esta lacuna foi superada até certo ponto em alguns compósitos de vidro metálico a granel à base de CuZr (BMGCs) aprimorados por partículas de CuZr de fase B2 dúctil [3, 7,8,9,10,11]. Além disso, algumas precipitações de CuZr cristalino B2 seriam inerentemente formadas através da cristalização em vidro CuZr sob carregamento, e então sofreriam geminação e deslocamento de deslocamento, induzindo a mudança nas propriedades mecânicas dos BMGs, como foi encontrado no experimento [12]. Para endurecer BMGs com precipitações CuZr de fase B2 e projetar BMGs de alto desempenho, os comportamentos de deformação de CuZr de fase B2 devem ser esclarecidos em primeiro lugar.
O CuZr da fase B2 é um tipo de liga com memória de forma que tem a capacidade de recuperar sua forma original sob condições termo-mecânicas específicas [13, 14], o que é diferente dos materiais cristalinos tradicionais que têm deslizamento de deslocamento ou geminação como o principal mecanismo de deformação [15,16,17]. O cálculo do primeiro princípio baseado na teoria da densidade funcional pode ser usado para estudar o processo de adsorção [18,19,20] e a propriedade interfacial [21, 22], mas não pode ser aplicado para estudar a evolução dinâmica dos comportamentos de transição de fase devido à limitação da escala de cálculo. A simulação de dinâmica molecular (DM) é um método eficaz para estudar as propriedades mecânicas e comportamentos de deformação de materiais [23,24,25,26,27,28,29,30,31]. Sutrakar e Mahapatra investigaram os efeitos das dimensões transversais e da temperatura na transformação de fase em nanofios de Cu-Zr, bem como a assimetria tensão-compressão por simulação MD [32,33,34], e obtiveram alguns resultados valiosos. Por exemplo, a fase B2 inicial é transformada em uma fase tetragonal centrada no corpo (BCT) pela nucleação e propagação de um plano de geminação {100}. Amigo et al. usaram dois tipos de potenciais [35, 36] em suas simulações de MD para investigar os comportamentos de transformação de fase e descobriram que um produz a transformação martensítica de B2 para a estrutura BCT, enquanto o outro não [13].
Sabe-se que a anisotropia dos cristais desempenha um papel importante na deformação dos materiais. Diferentes mecanismos de deformação podem desempenhar papéis dominantes durante a deformação quando a carga é aplicada ao longo de diferentes orientações de cristal [37]. Por exemplo, deslizamento de deslocamento perfeito e geminação são os principais mecanismos de deformação para a nanoindentação em (001) e (111) superfícies de nitreto de vanádio (VN) com um indentador cilíndrico [38, 39], respectivamente, mostrando plasticidade anisotrópica óbvia. Para o nanofio de ferro BCC, a transformação de fase mostra uma dependência intrincada da orientação cristalográfica, ao longo da qual a carga é aplicada, o fio orientado <001> exibe uma transformação BCC → FCC, mas o fio orientado <011> e <111> segue um BCC → Transformação HCP [40]. A matriz de distribuição atômica na estrutura B2 é análoga àquela em uma estrutura BCC, mas há dois tipos de elementos na estrutura B2. A orientação do cristal das partículas de reforço em BMGs é geralmente dispersa, portanto, a direção de carregamento deve ter diferentes influências no efeito de tenacificação das diferentes partículas. Assim, é necessário estudar o comportamento de deformação das partículas de realce com carregamento em diferentes orientações.
Tensão e compressão uniaxial, como dois modos básicos de carregamento geralmente usados para avaliar as propriedades mecânicas fundamentais dos materiais. Neste trabalho, uma série de simulações de MD de tensão uniaxial e testes de compressão de CuZr cristalino B2 ao longo das orientações [001], [110] e [111] são conduzidas para explorar a dependência da transformação de fase na orientação de carregamento e na tensão e compressão (T / C) assimetria.
Métodos
O conhecido método de átomo incorporado (EAM) [41] é selecionado para descrever a força interatômica do sistema Cu-Zr. O potencial EAM tem sido amplamente utilizado para investigar o comportamento mecânico de metais e suas ligas [42,43,44,45,46]. Com base no quadro do EAM, Mendelev e seus colegas identificaram e otimizaram os parâmetros potenciais três vezes em 2007 [35], 2009 [36] e 2016 [47]. Neste trabalho, são utilizados os parâmetros da última versão do potencial interatômico para Cu-Zr [47] desenvolvido em 2016. Esses parâmetros podem produzir energia de falha de empilhamento estável e instável mais realista em comparação com o desenvolvido em 2009 [36], e podem descrever melhor as propriedades do CuZr cristalino.
Três amostras com o carregamento axial z ao longo de [001], [110] e [111] são preparados, respectivamente, como mostrado na Fig. 1. Antes de carregar, um algoritmo de gradiente conjugado (CG) é usado para minimizar a energia do sistema para alcançar um estábulo otimizado configuração. Os testes mecânicos são simulados em temperatura ambiente de 300 K. Em seguida, o sistema é relaxado com o conjunto NPT isotérmico-isobárico em T =300 K por 20 ps para atingir um estado de equilíbrio com condição livre de pressão. Verificou-se que o efeito da taxa de deformação do material nano-policristalino se torna insignificante, pois a taxa de deformação varia na faixa entre 5 × 10 8 e 1 × 10 9 s −1 , portanto, a taxa de deformação é atribuída como 1 × 10 9 s −1 considerando de forma abrangente a precisão e a eficiência do cálculo [48, 49]. Portanto, cada amostra é esticada / comprimida no z - direção a uma taxa de deformação de 10 9 s −1 durante o carregamento; entretanto, o conjunto NPT com Nose / Hoover barostat é empregado [50] para manter a pressão livre em x - e y -instruções. No relaxamento e no estágio de carregamento, as condições de contorno periódicas são aplicadas em x -, y -, e z -instruções.
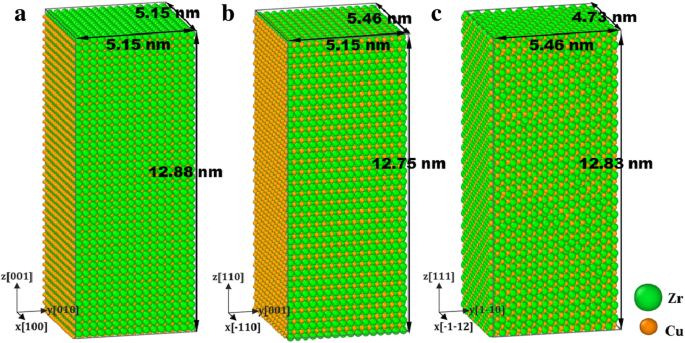
Amostras com z axial ao longo de a [001], b [110] e c [111], colorido com tipo atômico
A análise de vizinhança comum (CNA) [51], um algoritmo para caracterizar o ambiente estrutural local, é normalmente usada como um método eficaz para classificar os átomos em um sistema cristalino. A distância do segundo vizinho mais próximo em uma estrutura BCC é apenas 15% maior do que a mais próxima; portanto, o método CNA perderia alguma confiabilidade na presença de fortes flutuações térmicas e deformação. Para contornar este problema, o método de correspondência de molde poliédrico (PTM) foi proposto para classificar o ambiente estrutural local das partículas e identificar a estrutura cristalina local de fases condensadas simples (FCC, BCC, HCP, etc.) [52]. Comparado com o CNA [51], o método PTM promete maior confiabilidade na presença de fortes flutuações térmicas e deformações [52]. As estruturas B2 e BCC têm um arranjo atômico análogo; portanto, a estrutura BCC identificada por esse método é, na verdade, a estrutura B2. Após a análise da microestrutura local para os dados obtidos por simulação MD com PTM, os átomos são coloridos de acordo com as seguintes regras:azul para estrutura BCC (B2), verde para estrutura FCC, vermelho para falhas de empilhamento ou estrutura HCP, roxo para cúbico simples (SC) e branco para limites de grão ou núcleos de deslocamento. Deve-se observar que os átomos vermelhos de camada única, camada dupla e multicamadas contínuas são representados como limite duplo, falha de empilhamento e estrutura HCP, respectivamente. As regiões locais contendo átomos vermelhos, verdes, azuis e brancos são amorfos.
Como um método de análise de microestrutura suplementar, o parâmetro de centrossimetria (CSP) é usado para descrever a desordem local [53]. Para cada átomo, o CSP é calculado com a fórmula de fluxo:
$$ \ mathrm {CSP} \ kern0.5em =\ kern0.5em \ sum \ limits_ {i =1} ^ {N / 2} {\ left | {\ mathbf {R}} _ i + {\ mathbf {R}} _ {i + N / 2} \ right |} ^ 2, $$ (1)
onde N = 12 ou 8 é o número dos primeiros vizinhos mais próximos de um átomo central na estrutura FCC ou B2, e R i e R i + N / 2 são os vetores do átomo central para um par particular dos vizinhos mais próximos. O CSP é zero para um átomo cujos vizinhos mais próximos estão em seus locais de rede perfeitos. Se houver um defeito, como uma vacância ou deslocamento nas proximidades de um átomo, o CSP do átomo se tornará muito maior do que o causado pela vibração atômica local. O software aberto Ovito desenvolvido por Stukowski [54] é utilizado para exibir configurações atômicas.
Resultados e discussões
Curvas de tensão-tensão
A Figura 2 mostra a tensão-deformação ( σ - ε ) curvas para CuZr de fase B2 submetido a tensão uniaxial e compressão ao longo de [001], [110] e [111]. Pode-se notar que a tensão é maior do que no experimento [55], porque (1) a escala de tempo usada na simulação MD difere daquela usada no experimento, resultando em uma velocidade de indentação muito maior do que no experimento; e (2) os defeitos, incluindo defeito de ponto, deslocamentos e contornos de grão, etc., não são considerados nas simulações. No estágio inicial, essas curvas se desenvolvem linearmente e, em seguida, mostram tendências diferentes. Após o primeiro pico, essas curvas podem ser divididas em três grupos. No grupo I, as curvas caem rapidamente para níveis baixos de tensão, como compressão ao longo de [110] e [111]. No grupo II, as tensões caem para uma plataforma e flutuam com o aumento da deformação após o primeiro pico, como tensão ao longo [001], [110] e compressão ao longo [001]. As curvas então sobem para seus segundos picos antes da queda abrupta final. No grupo III, a curva cai rapidamente para níveis baixos de estresse e, em seguida, flutua em um padrão de ziguezague, como a tensão ao longo [111]. Antes do primeiro pico, as amostras permanecem na estrutura B2 e nenhum deslocamento de deslocamento óbvio e geminação podem ser observados, o que pode ser considerado como a deformação elástica. No estágio linear elástico, o módulo de Young E pode ser obtido ajustando a inclinação de cada curva no intervalo de 0,00 < ε <0,02, e listados na Tabela 1, onde pode ser visto que a orientação [001] é a mais suave e [111] é a mais rígida. Isso está de acordo com os resultados do ferro BCC a granel [40]. O E da amostra sob compressão é maior do que sob tensão exceto pela orientação [001], em consistência com a observada no cristal único de Cu [56], que deve ser atribuída ao maior atrito sob compressão [56]. O resto das curvas no estágio elástico sob compressão desviam-se obviamente daquelas sob tensão, o que deve ser atribuído à tração assimétrica e natureza compressiva do potencial interatômico [57]. Após o primeiro pico, não está claro se a deformação deve ser atribuída a deslizamento de deslocamento ou transformação de fase; portanto, esta região não pode ser vista como assimetria T / C inelástica ou plástica, o que difere de trabalhos de outros [57,58,59]. Na seção de escoamento, os mecanismos de deformação da amostra submetida a carregamentos ao longo de diferentes direções serão discutidos em detalhes.
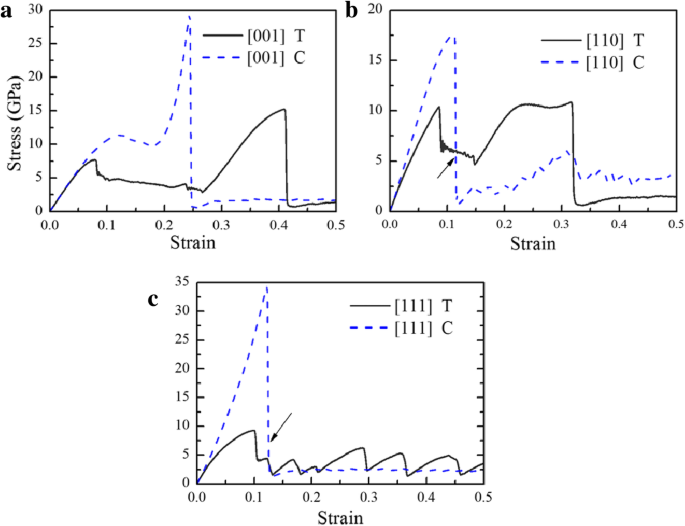
σ - ε curvas de amostras sob tensão (T) e compressão (C). a [001], b [110] e c [111]
Comportamento de falha
A Figura 3 mostra as estruturas atômicas e as funções de distribuição radial (RDFs) das amostras submetidas à compressão ao longo de [110] e [111], cujos σ - ε curvas podem ser vistas na Fig. 2 rotuladas como [110] C e [111] C. A Figura 3a, d mostra as amostras iniciais [110] e [111] após o relaxamento a 300 K, onde pode ser visto que os átomos são na estrutura B2. Quando ε for aumentado para 0,115 ou 0,125 para [110] C e [111] C, respectivamente, a região com estruturas mistas aparece, como mostrado na Fig. 3b, f. A estrutura na área mista é definida como uma fase mista. A nucleação da fase mista corresponde ao estágio de queda rápida das curvas [110] C e [111] C na Fig. 2b, c, que é marcada com setas. Portanto, a transformação da estrutura local de B2 para uma fase mista causa a rápida queda do estresse. No estágio de escoamento, a variação da fração de volume da fase mista é o principal mecanismo para acomodar mais deformações, as estruturas locais nas amostras sob compressão ao longo de [110] e [111] em ε =0,25 são mostrados na Fig. 3c, g, respectivamente. Para especificar a estrutura na região mista, a função de distribuição radial ( RDFs ), g ( r ), das amostras sob compressão ao longo de [110] e [111] em diferentes deformações são mostradas na Fig. 3d, h. Os picos do g ( r ) das amostras em ε =0 e ε =0,25 são nítidos, indicando que ainda mantêm a característica cristalina. Enquanto os picos do g ( r ) para as regiões mistas, isto é, a amostra sem regiões B2, são rombas, exceto as primeiras, indicando que a região mista está em um estado amorfo. O algoritmo de extração de deslocamento (DXA) [60] também é usado para detectar se há qualquer nucleação de deslocamento e não encontrar deslocamentos óbvios ao longo do processo de deformação. Portanto, a amorfização da fase B2 é conduzida para ser o modo de falha principal, resultando na queda rápida, marcada com setas na Fig. 2b, c.
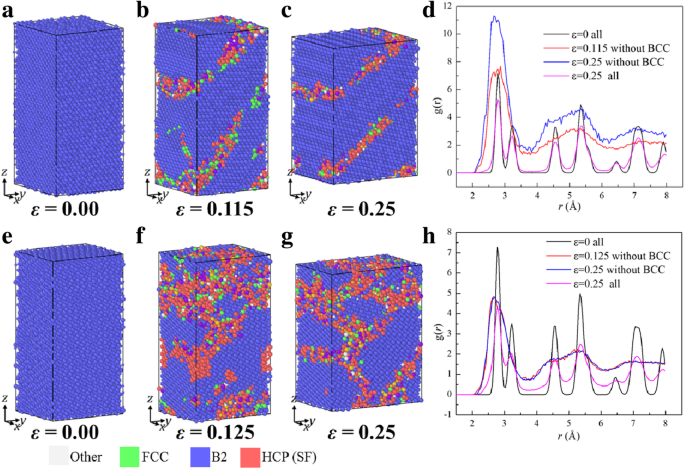
Configurações atômicas e RDFs de amostras sob compressão. a - d Junto [110] e e - h ao longo de [111]
A Figura 4 mostra as configurações atômicas após a deformação de queda rápida (deformação de falha) das amostras sob tensão ao longo de [001], [110] e compressão ao longo de [001], cujo σ - ε as curvas pertencem ao grupo II. Pode-se observar na Fig. 4 que se formam regiões mistas, semelhante ao grupo I, indicando que a amorfização também é o principal modo de falha (Fig. 4). No entanto, essas regiões misturadas são circundadas por átomos verdes e vermelhos (estrutura FCC e HCP), que é diferente da estrutura B2 na Fig. 3. Essa diferença indica que a fase mista é transformada da estrutura B2 sob compressão na Fig. 3, mas do FCC para a amostra [001] sob tensão e compressão e do HCP para a amostra [110] sob tensão.
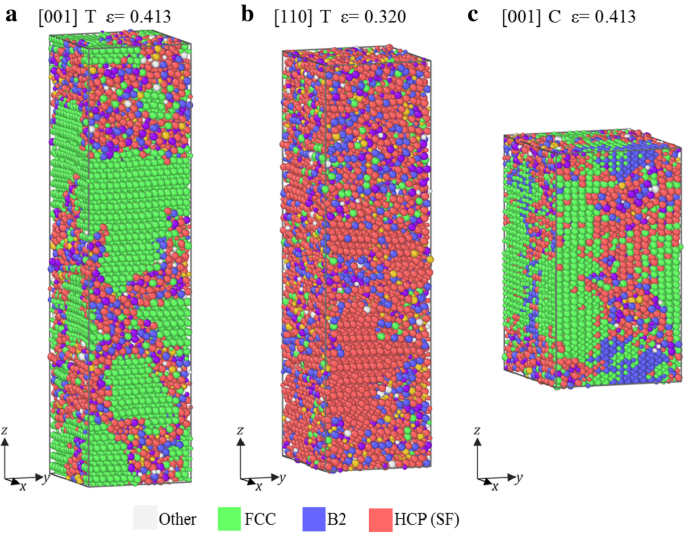
Configurações atômicas em amostras na cepa de falha. a Sob tensão ao longo de [001], b sob tensão ao longo de [110], e c sob compressão ao longo de [111]
Transformações de fase
A Figura 5 mostra o σ - ε curva da amostra [001] sob tensão, onde também são exibidas as microestruturas em pontos típicos (marcados com A, B, ..., G). Os átomos no ponto A ( ε =0,079) estão na estrutura B2, indicando que antes de ε =0,079 a deformação na amostra é elástica. No entanto, a transformação local de B2 para FCC ocorre, conforme mostrado na inserção de ε =0,082 na Fig. 5, resultando na primeira queda rápida (A → B) para ε =0,082, onde a liberação da energia elástica armazenada devido à redistribuição da configuração atômica fornece a energia para a necessidade da transformação de fase. No estágio de fluxo de B → F, a energia elástica armazenada é posteriormente liberada conforme a transformação de fase continua, levando à redução do estresse. A estrutura local da amostra torna-se FCC completamente em ε =0,242 (ponto E). E a estrutura continua mudando entre os pontos E e F, mas a tensão continua caindo com o aumento da deformação. Para revelar a mudança da microestrutura, a distribuição de g ( r ) e a variação do número de átomos ( N ) contra CSP ( N - CSP ) da amostra em ε =0,242, 0,254 e 0,267 (entre os pontos E e F) são calculados e mostrados na Fig. 6a, b, respectivamente, onde a altura de cada pico aumenta com o aumento da deformação, indicando que o sistema se torna mais compacto.
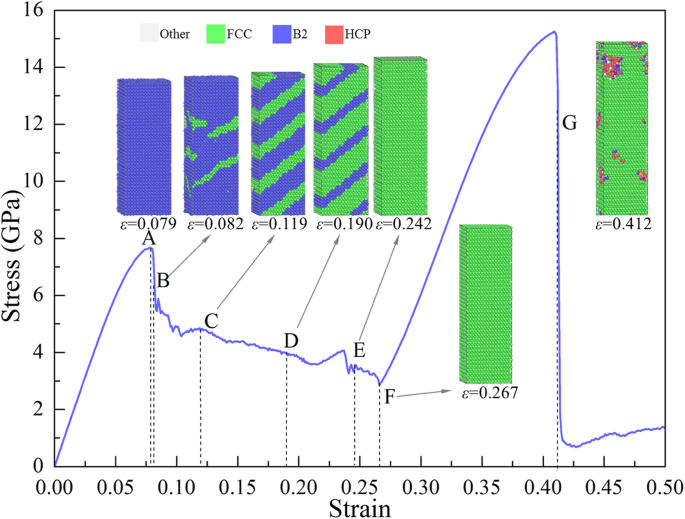
σ-ε curva da amostra sob tensão ao longo de [001], colorida com a estrutura local, com azul, verde e vermelho representando as fases B2, FCC e amorfa, respectivamente
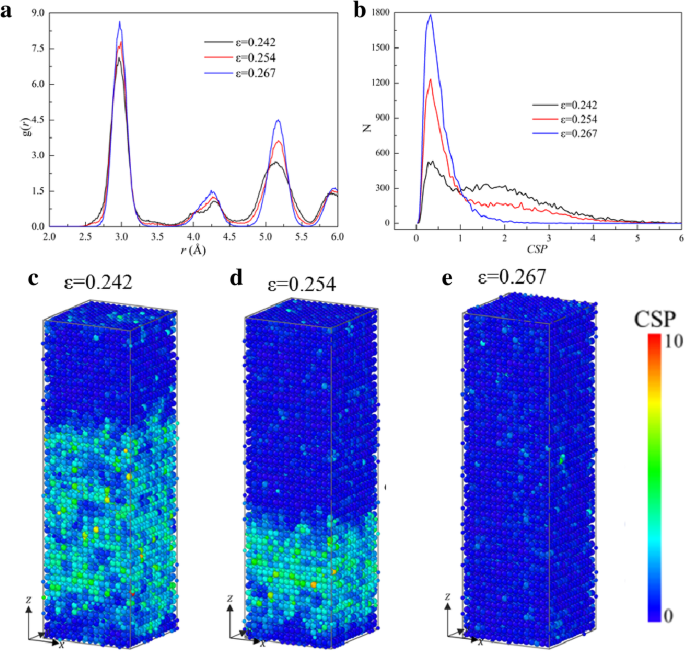
a RDF , b N - CSP parcelas de amostra sob tensão ao longo de [001]. c - e Distribuição de CSP na amostra em diferentes cepas
Para caracterizar se um átomo é parte de uma rede perfeita ou um defeito local, por exemplo, um deslocamento ou falha de empilhamento, ou uma superfície, o CSP [53] dos átomos com o número de vizinhos mais próximos da estrutura FCC ( N =12) são calculados, conforme mostrado na Fig. 6c – e. E um CSP maior significa um desvio maior da rede perfeita [17]. Pode ser visto na Fig. 6b que o número de átomos com CSP <1 aumenta com o aumento da deformação, o que também pode ser visto de forma mais intuitiva a partir da distribuição de CSPs de átomos na Fig. 6c-e. É diferente dos resultados comuns que geralmente CSP não diminuiria com o aumento da deformação. Portanto, os principais comportamentos de deformação nesta fase também devem ser atribuídos à transformação de fase de FCC imperfeito para FCC perfeito. Na fase de escoamento, a amostra com estruturas FCC é alongada, e o estresse aumentará até atingir o segundo limite de escoamento. Em seguida, a curva cai abruptamente, correspondendo à amorfização local ao invés da nucleação de deslocamento ou escorregamento.
Para ilustrar a transformação de fase do material durante a deformação, a Fig. 7 mostra alguns yoz fatias da amostra [001] sob tensão em diferentes cepas. As linhas tracejadas horizontais e verticais são usadas como referências para identificar se as estruturas atômicas giram e se desviam. Com o aumento de ε de 0,0 a 0,079, os átomos encontram-se em linhas paralelas aos eixos horizontal e vertical, indicando que são da estrutura local B2. No entanto, a matriz atômica na Fig. 7b muda para aquela na Fig. 7c como ε de 0,079 a 0,119 quando algumas estruturas B2 se transformam na estrutura FCC. O ângulo entre os arranjos muda de 90 ° na Fig. 7b para a estrutura B2 para ~ 85 ° na Fig. 7c para a estrutura FCC com a orientação da rede desviando do eixo vertical em 5 ° no sentido horário, mas o arranjo atômico da estrutura B2 não muda obviamente e não tem rotação óbvia. Durante 0,119 < ε < 0,190, a área FCC aumenta e a matriz de átomos verdes gira gradualmente no sentido anti-horário. Em ε =0,242, toda a estrutura B2 se transforma em estruturas FCC, como mostrado na Fig. 7e, onde as três orientações da rede tornam-se quase paralelas com os três eixos respectivamente, mas ainda há um desvio marcado, indicando que a estrutura FCC não é perfeita, o que é em consistência com o mostrado na Fig. 6c. No estágio de fluxo, a matriz atômica tende regularmente, como mostrado na Fig. 7f em ε =0,267, que é reconhecido como um plano {110} da estrutura FCC, com sua orientação de cristal nas direções horizontal e vertical alterada de [010] e [001] da estrutura B2 para <110> e <001> da estrutura FCC.
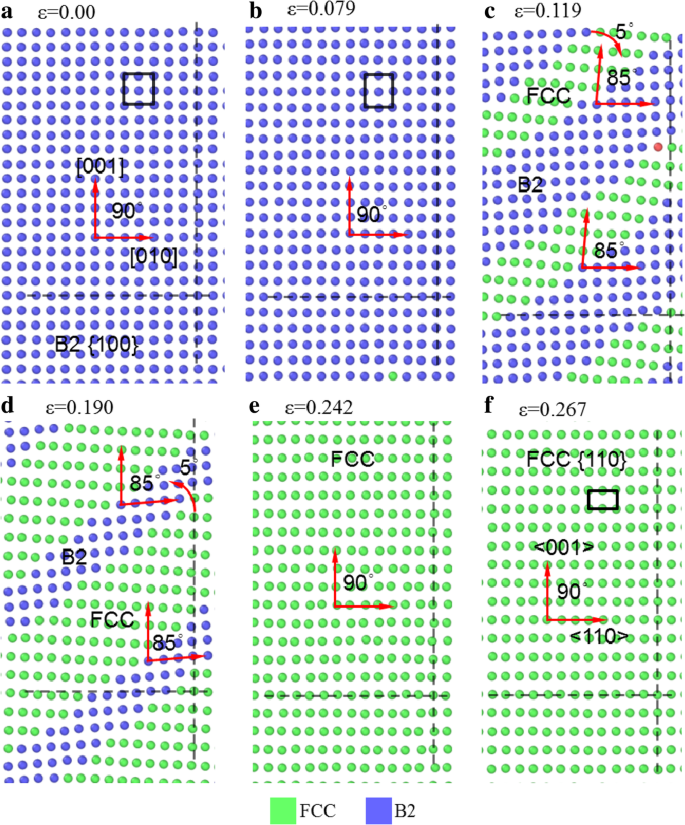
yoz fatias de [001] amostra sob tensão em diferentes cepas, coloridas com uma estrutura de rede local, com azul, verde e vermelho representando as fases B2, FCC e amorfa, respectivamente
A simulação para a resposta da amostra (100) durante o descarregamento de diferentes tensões máximas de tração ( ε máximo =0,1, 0,2 e 0,3, respectivamente) são realizados, e o σ - ε curvas são mostradas na Fig. 8. Pode-se observar que o descarregamento σ - ε curvas entre ε =0,266 e ε =0,056 não se sobrepõem à curva de carregamento, mas podem se encontrar com o elástico σ - ε curva em ε =0,056 e depois retornar à origem ao longo do elástico σ - ε curva, exibindo a característica superelástica. Os caminhos de carga e descarga formam loops de histerese, que devem ser atribuídos aos diferentes caminhos de encaminhamento e transformações de fase inversa.
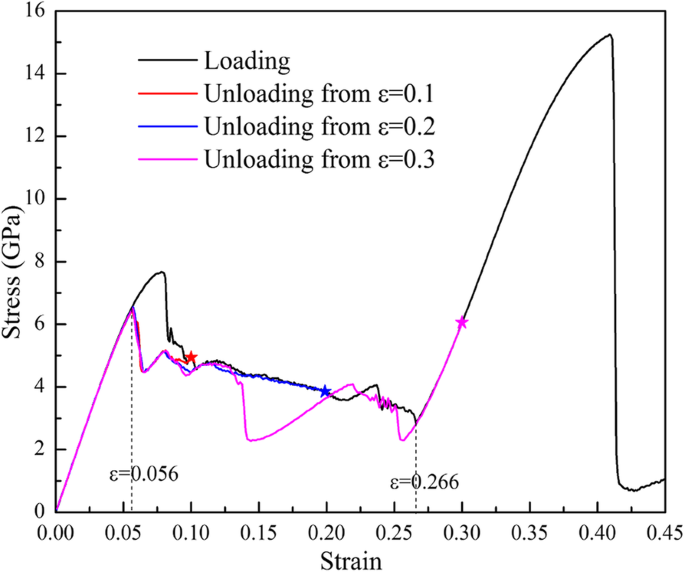
Carregando e descarregando σ - ε curvas de tensão ao longo [001] de diferentes deformações
O σ - ε curva da amostra [001] sob compressão tem uma tendência semelhante, conforme mostrado na Fig. 9a, que pode ser dividida em quatro estágios:(1) σ aumenta linearmente com o aumento da deformação; (2) σ cai para um platô; (3) σ aumenta linearmente com uma inclinação maior para o segundo pico conforme o aumento da deformação; (4) σ cai drasticamente para o segundo platô. Ao analisar as estruturas locais com PTM, pode-se descobrir que a maioria dos átomos são identificados como estrutura B2 antes de atingir o segundo pico, exceto alguns átomos espalhados que são identificados como outra estrutura local, como mostrado na Fig. 9a. No entanto, de acordo com o entendimento anterior, uma mudança repentina no σ - ε curvas geralmente correspondem à mudança da microestrutura. Para confirmar ainda mais, o N - CSP os gráficos são calculados e mostrados na Fig. 9b, em que o CSP para cada átomo em diferentes cepas é calculado com os vizinhos mais próximos da estrutura B2 ( N =8). Quando ε =0, o CSP de átomos é maior que 0, mas menor que 1, devido ao efeito da temperatura, o que implica que os átomos estão em perfeita estrutura B2. Com o aumento de ε , os átomos podem ser divididos em dois grupos por seus CSPs:CSP <1 e 5
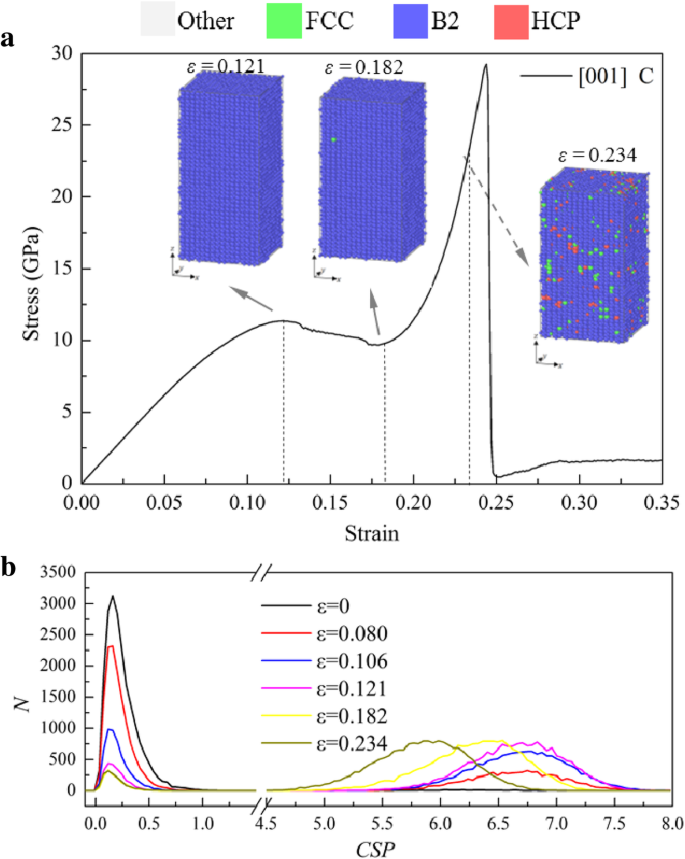
Respostas da amostra [001] sob compressão. a σ-ε curva e configurações atômicas típicas, com átomos coloridos com estruturas locais identificadas por PTM. b N - CSP tramas
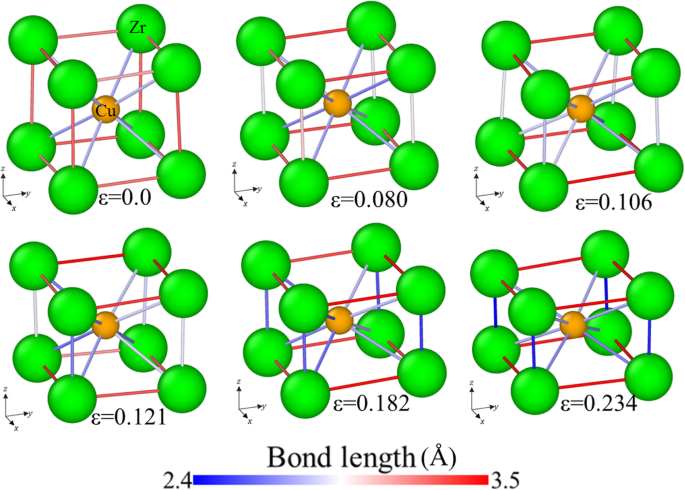
Evolução do comprimento da ligação para a amostra [001] sob compressão, com ligações coloridas com seu comprimento
A Figura 11a mostra a resposta da amostra [110] sob tensão. O primeiro pico (ponto A) corresponde ao limite de rendimento da estrutura B2, então alguma estrutura local B2 se transforma na estrutura HCP, resultando na queda acentuada. Com o aumento de ε , a tensão diminui até o ponto C quando a amostra é totalmente transformada em HCP. Figura 11b, c é o xoy fatias de uma camada em ε =0 e 0,150, respectivamente, onde se pode ver que no estágio inicial os átomos de Cu e Zr estão em uma camada atômica idêntica (Fig. 11b). No entanto, os átomos de Cu e Zr são separados em camadas adjacentes em ε =0,150 (Fig. 11c), que resulta na transformação de fase de B2 para HCP. Então, com o aumento de ε , σ aumenta com uma inclinação menor do que no estágio linear inicial até o ponto D, seguido por uma queda acentuada para um nível de baixa tensão, correspondendo a falha devido à amorfização local.
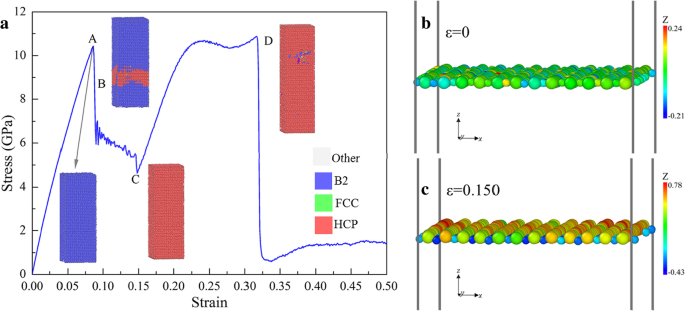
a Comportamento de deformação da tensão ao longo de [110], colorido com PTM. b , c Fatias atômicas em xoy plano em ε =0 e 0,150, respectivamente
Conclusões
Neste trabalho, as respostas e a transformação de fase de amostras CuZr submetidas à tensão uniaxial e compressão ao longo de [001], [110], [111] orientações são estudadas respectivamente usando simulações de dinâmica molecular, fazendo uso do potencial interatômico mais recente, a partir do qual o as seguintes conclusões principais podem ser tiradas:
- 1.
As respostas mecânicas das amostras CuZr sob tensão e sob compressão exibem assimetria óbvia, e seu principal mecanismo de falha deve ser a amorfização local.
- 2.
Existem três tipos de transformações de fase:B2 → FCC, B2 → BCT e B2 → HCP em tração e compressão ao longo de [001] e tensão ao longo de [110].
- 3.
As transformações de fase B2 → FCC, B2 → BCT e B2 → HCP são realizadas por mecanismos únicos, respectivamente, que são rotação da rede (~ 5 °), deformação uniforme e separação da camada atômica de Cu e Zr para cada uma.
- 4.
A região de transformação de fase pode ser recuperada após o descarregamento antes da amorfização local, mostrando a superelasticidade.
Os resultados são importantes para a exploração das propriedades mecânicas e mecanismos de deformação do CuZr nanocristalino, e para as aplicações de partículas de CuZr nanocristalino como um agente de intensificação para melhorar a tenacidade do vidro metálico.
Disponibilidade de dados e materiais
Os conjuntos de dados usados ou analisados durante o estudo atual estão disponíveis junto ao autor correspondente, mediante solicitação razoável.
Abreviações
- BCC:
-
Cúbico centrado no corpo
- BCT:
-
Corpo-centrado-tetragonal
- BMG:
-
Vidros metálicos a granel
- BMGC:
-
Compósitos de vidro metálico a granel
- CG:
-
Gradiente conjugado
- CNA:
-
Análise de vizinho comum
- CSP:
-
Parâmetro de simetria centro
- Cu:
-
Cobre
- CuZr:
-
Cobre-zircônio
- DXA:
-
Algoritmo de extração de deslocamento
- EAM:
-
Método de átomo incorporado
- FCC:
-
Cúbico centrado no rosto
- HCP:
-
Hexagonal fechado
- MD:
-
Dinâmica Molecular
- NPT:
-
Número constante de partículas, pressão e temperatura
- PTM:
-
Correspondência de modelo poliédrico
- RDF:
-
Função de distribuição radial
- T / C:
-
Tensão e compressão
- VN:
-
Nitreto de vanádio
- Zr:
-
Zircônio
- ε :
-
Variedade
- σ :
-
Estresse
Nanomateriais



