Polarização de vale controlável usando Silicene de defeitos de linha dupla devido ao acoplamento Rashba Spin-Orbit
Resumo
Teoricamente, investigamos a polarização de vale em siliceno com dois defeitos de linha paralela devido ao acoplamento Rashba spin-orbit (RSOC). Verificou-se que, enquanto RSOC exceder o acoplamento spin-orbit intrínseco (SOC), os coeficientes de transmissão dos dois vales oscilam com a mesma periodicidade e intensidade, que consiste em picos de transmissão largos e platôs de transmissão zero. Porém, na presença de um campo elétrico perpendicular, a periodicidade de oscilação do primeiro vale aumenta, enquanto a do segundo vale encurta, gerando as correspondentes regiões de pico-zero planaltos, onde a polarização perfeita do vale pode ser alcançada. Além disso, a polarizabilidade do vale pode ser alterada de 1 para -1 controlando a intensidade do campo elétrico. Nossas descobertas estabelecem uma rota diferente para a geração de corrente polarizada por vale por meios puramente elétricos e abrem a porta para aplicações interessantes de Valleytronics de semicondutores.
Introdução
O siliceno, uma estrutura em favo de mel de monocamada de baixa curvatura de átomos de silício, é uma alternativa potencialmente atraente ao grafeno para aplicações Valleytronic. A estrutura de baixa curvatura dá origem a um acoplamento spin-órbita (SOC) relativamente grande em siliceno, e uma lacuna de energia considerável de aproximadamente 1,55 meV é estimada nos pontos de Dirac K e K ′ [1] Diferente do grafeno, a relação de dispersão de baixa energia do siliceno é parabólica ao invés de forma linear. Facilitada pela estrutura de flambagem, a estrutura da banda de siliceno pode ser controlada pela aplicação de um campo elétrico, e até mesmo uma transição de fase topológica de um isolador Hall quântico de spin para um isolador Hall quântico Valley pode ocorrer [2, 3]. O siliceno foi sintetizado com sucesso na superfície de substratos como Ag (111), Ir (111) e ZrB2 (0001) [4-6], e sua estrutura estável independente também foi prevista em vários estudos teóricos [7 ] Mais importante ainda, um transistor de efeito de campo de siliceno (FET) à temperatura ambiente foi observado experimentalmente [8]. A sintonia do campo elétrico e a compatibilidade com os dispositivos existentes à base de silício tornam o siliceno um material bidimensional potencial para aplicação em Valleytronics de próxima geração.
Em materiais bidimensionais (2D), como grafeno e dichalcogenetos de metais de transição (MoS 2 , etc.), os limites de grão entre dois domínios de material com diferentes orientações cristalográficas são escolhas ideais para atingir a polarização de vale e tem atraído considerável atenção [9-14]. Recentemente, os defeitos de linha estendida (ELDs) em siliceno foram extensivamente investigados de acordo com cálculos de primeiros princípios [15, 16], e o 5-5-8 ELD (abreviado como "defeito de linha" a seguir) foi considerado a estrutura mais estável e mais facilmente formada. A polarização de spin e vale do defeito da linha de siliceno foi investigada teoricamente [17-19]. A formação de um defeito da linha pode ser visualizada como a costura das bordas em zigue-zague de dois grãos de Si por os átomos de Si adsorvidos, onde cada lado do defeito da linha mostra um comportamento semelhante a um estado de pseudoedge e os limites de grão da borda do zigue-zague agem como a pseudo-borda [16]. Obviamente, tal rede tem simetria de espelho em relação à linha defeito e os vetores de rede correspondentes nos domínios "esquerdo" e "direito" separados pelo defeito são contrários [10, 11]. Em tal defeito de linha com contorno de domínio de inversão, o A / B sub-redes e índices de vale são trocados ao cruzar o defeito. O defeito da linha é semitransparente para as quasipartículas no grafeno e uma alta polarização de vale aparece com um alto ângulo de incidência. A polarização do vale é q y (a velocidade do grupo do elétron ao longo do y direção) dependente do defeito da linha. Para o grafeno, que tem uma dispersão linear e velocidade de grupo constante, a polarização de vale pode chegar perto de 100% em grande | q y | (correspondendo a alto ângulo de incidência) enquanto diminui à medida que | q y | diminui e desaparece quando | q y | ∼0 [9, 14]. Em contraste, o siliceno tem duas características de transmissão diferentes [17, 18]:em primeiro lugar, os dois vales tornam-se indistinguíveis porque a energia de Fermi está perto da borda da banda devido à relação de dispersão parabólica e, em segundo lugar, a transmissão é restringida por causa do helicoidal estado de borda fluindo inversamente em ambos os lados do defeito da linha, como mostrado na Fig. 1c. Naturalmente, o sistema com SOC em um RSOC particular é um candidato promissor para um FET de spin eficiente. O RSOC gera um campo magnético efetivo no plano e induz a precessão do spin que é injetada perpendicularmente ao plano de confinamento. A polarização de spin [20] e a inversão [21] foram investigadas em nanofitas de siliceno gated. Cálculos teóricos mostraram que a banda de energia do siliceno pode ser modulada significativamente pelo RSOC [22, 23]. Por exemplo, em um RSOC relativamente forte, a banda de spin-down (-up) no K ( K ′ ) vale se desloca para cima enquanto as outras bandas de spin na banda de condução permanecem inalteradas. Em consideração à característica de transmissão peculiar no defeito da linha de siliceno e o efeito do RSOC no siliceno, os esquemas totalmente elétricos para a geração de portadores polarizados de vale tornam-se viáveis.
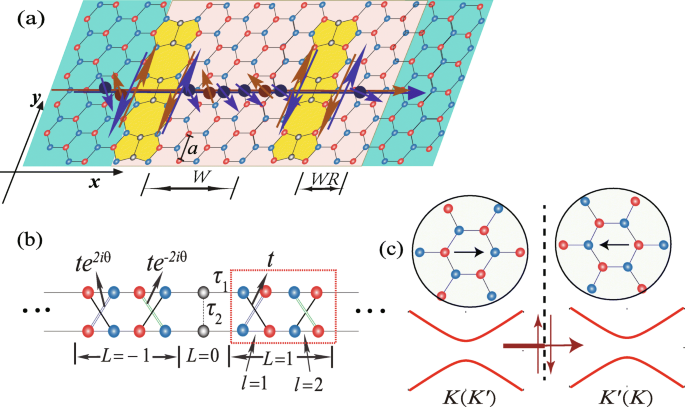
a Diagrama esquemático do processo de precessão dos estados ( K , ↑ ) (esfera vermelha) e ( K ′ , ↓ ) (esfera azul) através de uma folha de siliceno com dois defeitos de linha paralela, onde o círculo azul (vermelho) denota o A ( B ) subrede. Os estados ( K , ↑ ) e ( K ′ , ↓ ) circulam ao longo da pseudo-aresta, e o RSOC, bem como o campo elétrico, presume-se que exista na região cinza francesa. W ( W =2) e WR ( WR =1) representam a largura da região de espalhamento em unidades de \ (\ sqrt {3} a \). b O modelo de rede simplificado do siliceno infinito com um defeito de linha, onde θ = k y a e o retângulo pontilhado corresponde a uma supercélula. Na célula unitária, os pontos da rede são especificados por um conjunto de índices ( L, l ) c A transmissão para um estado de spin no K ( K ′ ) vale através do defeito de linha com limites de domínio de inversão. As inserções mostram a orientação da rede cristalina nos dois domínios separados pelo defeito da linha (linha tracejada). As linhas grossas / finas indicam que a transmissão é restringida através do defeito da linha devido aos estados de borda helicoidal fluindo inversamente ao longo da pseudoargila
Neste artigo, propomos uma maneira eficiente de polarizar os férmions de Dirac de diferentes vales usando os defeitos de linha dupla de siliceno, criando assim uma polarização de vale distinta, utilizando o campo elétrico no siliceno. Nossos resultados mostram que quando a energia de Fermi está perto da parte inferior da banda de condução, as imagens de oscilação dos coeficientes de transmissão de dois vales, que compreendem amplos picos e nadirs oscilantes, coincidem desde que RSOC exceda o SOC intrínseco, enquanto a presença de apenas um único defeito de linha não pode dispersar os elétrons dependentes do vale. Quando dois defeitos de linha paralela estão envolvidos, os nadires oscilantes evoluem para planaltos de transmissão zero, e a modulação efetiva do transporte dependente do vale pode ser realizada mudando a periodicidade de oscilação dos dois vales de Dirac com um campo elétrico perpendicular, onde a periodicidade de oscilação de os dois vales aumentam e diminuem e levam à polarização perfeita do vale nas regiões correspondentes do platô de pico zero. No experimento, pode-se detectar essa corrente de vale pura medindo a mudança de condutância com o campo elétrico. Este fenômeno fornece uma rota diferente para modular efetivamente a polarização de vale em dispositivos de siliceno, utilizando o RSOC e campos elétricos.
Métodos
Vamos começar com o esquema de um dispositivo de defeito de linha de siliceno de dois terminais, como mostrado na Fig. 1a, em que a precessão do spin é ilustrada para gerar a corrente polarizada em vale devido ao RSOC e ao campo elétrico. Supõe-se que RSOC existe em um lado do defeito da linha com largura W e WR em unidades de \ (\ sqrt {3} a \), onde a =3,86 Å é a constante de rede do siliceno primitivo, como mostrado na Fig. 1a. Quando a energia de Fermi está localizada na parte inferior da banda de condução, os estados ( K , ↓ ) [( K , ↓ ) corresponde a um estado no vale K com ↓ (para baixo) girar] e ( K ′ , ↑ ) estão na lacuna devido à manipulação da banda de energia do RSOC. Os outros dois estados, ( K , ↑ ) e ( K ′ , ↓ ), circulam ao longo da pseudo-aresta por causa da característica de bloqueio do momento de rotação do SOC [24], conforme mostrado na Fig. 1a. Para um estado de spin definido, ele flui ao longo da pseudo-aresta com direções opostas em ambos os lados do defeito da linha, que pode atuar como um filtro e restringir a transmissão através do defeito da linha, conforme ilustrado na Fig. 1c.
Um modelo de rede na representação de ligação estreita é usado para descrever o sistema de defeito de linha com RSOC como [17, 22]
$$ \ begin {array} {@ {} rcl @ {}} H &=&t \ sum _ {\ langle i, j \ rangle \ alpha} c_ {i \ alpha} ^ {\ dag} c_ {j \ alpha} + \ tau_ {2} \ sum _ {\ langle \ gamma \ delta \ rangle \ alpha} c_ {i_ {y} \ alpha, \ gamma} ^ {\ dag} c_ {i_ {y} \ alpha, \ delta} + \ tau_ {1} \ sum _ {\ langle i, \ gamma \ rangle \ alpha} c_ {i \ alpha} ^ {\ dag} c_ {i_ {y} \ alpha, \ gamma} \\ &+ &i \ frac {t_ {so}} {3 \ sqrt {3}} \ sum _ {\ langle \ langle i, j \ rangle \ rangle \ alpha \ beta} \ nu_ {ij} c ^ {\ dag} _ {i \ alpha} \ sigma_ {\ alpha \ beta} ^ {z} c_ {j \ beta} + \ Delta_ {z} \ sum_ {i \ alpha} \ mu_ {i} c_ {i \ alpha} ^ {\ dag} c_ {i \ alpha } \\ &+ &it_ {R} \ sum _ {\ langle i, j \ rangle \ alpha \ beta} c_ {i \ alpha} ^ {\ dag} (\ vec {\ sigma} \ times \ mathrm {\ mathbf { d_ {ij}}}) ^ {z} _ {\ alpha \ beta} c_ {j \ beta} + Hc, \ end {array} $$ (1)
onde \ (c_ {i \ alpha} ^ {\ dag} \) e \ (c_ {i_ {y} \ alpha, \ gamma / \ delta} ^ {\ dag} \) representam o operador de criação de elétrons com spin α no site silicene i e o defeito da linha, respectivamente, e 〈〉 / 〈〈 〉〉 percorre todos os locais de salto mais próximo / próximo ao vizinho mais próximo. Os primeiros três termos denotam salto do vizinho mais próximo e os parâmetros t , τ 1 , e τ 2 denotam várias energias de salto do vizinho mais próximo no modelo de ligação forte, como mostrado na Fig. 1b. O quarto termo é o SOC efetivo com o parâmetro de salto t então e ν ij =± 1 para o salto no sentido anti-horário (sentido horário) entre os sites vizinhos mais próximos em relação ao z positivo -eixo. Uma investigação teórica [16] mostrou que os dois átomos de Si mais próximos na região do defeito são relativamente idênticos aos da região prístina e que todos os átomos de Si permanecem no sp 2 - sp 3 estado hibridizado. Portanto, é razoável definir τ 2 = τ 1 = t . No quinto mandato, Δ z é o potencial de sub-rede escalonado que surge de um campo elétrico perpendicular à folha de siliceno, e μ i =± 1 para o A ( B ) local. O último termo representa o termo RSOC extrínseco onde t R é o parâmetro de salto de rotação-órbita Rashba. d ij é o vetor de unidade que aponta do site j para i , e \ (\ vec {\ sigma} =(\ sigma ^ {x}, \ sigma ^ {y}, \ sigma ^ {z}) \) na Eq. 1 é o vetor de matrizes de Pauli de spin real. O RSOC surge do potencial externo aplicado por uma porta elétrica, adsorção de átomo de metal ou substratos [20, 25] que pode quebrar drasticamente a simetria de inversão da estrutura do siliceno. Notavelmente, o RSOC extrínseco originado do campo elétrico é ignorado porque é muito fraco.
Os ELDs de siliceno são mostrados na Fig. 1a, que se estende imensamente ao longo do y direção. A simetria translacional da estrutura da rede ao longo do y direção indica que k y é uma quantidade conservada e que os operadores de criação (aniquilação) podem ser reescritos da seguinte forma, de acordo com a transformação de Fourier (o índice de spin é ignorado) [17]:
$$ \ begin {array} {@ {} rcl @ {}} c_ {i} ^ {\ dag} =\ sum_ {k_ {y}} c_ {k_ {y}, i_ {x}} e ^ {- 2ik_ {y} i_ {y} a}, c_ {i} =\ sum_ {k_ {y}} c_ {k_ {y}, i_ {x}} e ^ {2ik_ {y} i_ {y} a}, \\ c_ {i_ {y}, \ gamma} ^ {\ dag} =\ sum_ {k_ {y}, \ gamma} c ^ {\ dag} _ {k_ {y}, \ gamma} e ^ {- 2ik_ {y} i_ {y} a}, c_ {i_ {y}, \ gamma} =\ sum_ {k_ {y}, \ gamma} c_ {k_ {y}, \ gamma} e ^ {2ik_ {y} i_ {y} a}. \ end {array} $$ (2)
Então, a matriz hamiltoniana na Eq. 1 é desacoplado em \ (H =\ sum _ {k_ {y}} H_ {k_ {y}} \), onde \ (H_ {k_ {y}} \) pode ser descrito da seguinte forma:
$$ {\ begin {alinhados} H_ {k_ {y}} =- \ sum_ {i} \ varphi_ {i, 1} ^ {\ dag} \ hat {T} _ {11} \ varphi_ {i, 1} - \ sum_ {i} \ varphi_ {i, 2} ^ {\ dag} \ hat {T} _ {22} \ varphi_ {i, 2} \\ - \ sum_ {i} \ varphi_ {i, 1} ^ {\ dag} \ hat {T} _ {12} \ varphi_ {i, 2} - \ sum_ {i \ neq-1} \ varphi_ {i, 2} ^ {\ dag} \ hat {T} _ {23 } \ varphi_ {i + \ hat {x}, 1} \\ - \ varphi _ {\ bar {1}, 2} ^ {\ dag} \ hat {T} _ {\ bar {1} 0} \ varphi_ {0 } - \ varphi_ {0} ^ {\ dag} \ hat {T} _ {01} \ varphi_ {1,1} - \ varphi_ {0} ^ {\ dag} \ hat {T} _ {00} \ varphi_ {0} - \ varphi _ {\ bar {1}, 2} ^ {\ dag} \ hat {T} _ {\ bar {1} 1} \ varphi_ {1,1} + hc, \ end {alinhado}} $$ (3)
onde \ (\ varphi _ {i, l} ^ {\ dag} =\ left [c _ {{{k} _ {y}}, i, l, A \ uparrow} ^ {\ dag}, c _ {{{ k} _ {y}}, i, l, A \ downarrow} ^ {\ dag}, c _ {{{k} _ {y}}, i, l, B \ uparrow} ^ {\ dag}, c_ { {{k} _ {y}}, i, l, B \ downarrow} ^ {\ dag} \ right] \), i no conjunto de índice ( i, l ) representa a posição de uma supercélula \ ((\ bar {i} =- i) \), e l =1 ou 2 denota diferentes cadeias de zigue-zague em uma supercélula, como mostrado no retângulo tracejado na Fig. 1b. \ (\ hat {T_ {ll '}} \) representa a matriz Hamiltoniana de cada cadeia em ziguezague ( l = l ′ ) em uma supercélula ou a interação entre diferentes cadeias de zigue-zague ( l ≠ l ′ )
Observa-se que os dois vales K e K ′ agora são lançados em [0, ± π / 3 a ] devido à inserção do defeito da linha. A matriz de transmissão do η ( η = K / K ′ ) vale é calculado usando a fórmula generalizada de Landauer [26, 27],
$$ \ begin {array} {@ {} rcl @ {}} T ={\ left (\ begin {array} {cc} T ^ {\ uparrow \ uparrow} _ {\ eta} &T ^ {\ uparrow \ downarrow} _ {\ eta} \\ T ^ {\ downarrow \ uparrow} _ {\ eta} &T ^ {\ downarrow \ downarrow} _ {\ eta} \ end {array} \ right)} =\ sum_ {i , j =1} ^ {8} {\ left (\ begin {array} {cc} \ vert t_ {ij, \ eta} ^ {\ uparrow \ uparrow} \ vert ^ {2} &\ vert t_ {ij, \ eta} ^ {\ uparrow \ downarrow} \ vert ^ {2} \\ \ vert t_ {ij, \ eta} ^ {\ downarrow \ uparrow} \ vert ^ {2} &\ vert t_ {ij, \ eta} ^ {\ downarrow \ downarrow} \ vert ^ {2} \ end {array} \ right)}, \ end {array} $$ (4)
Onde
$$ \ begin {array} {@ {} rcl @ {}} t =2 \ sqrt {-Im \ Sigma_ {L}} G ^ {r} \ sqrt {-Im \ Sigma_ {R}} \ end {array } $$ (5)
e
$$ \ begin {array} {@ {} rcl @ {}} t_ {ij, \ eta} ^ {\ uparrow \ uparrow} &=t_ {2 (i-1) +1,2 (j-1) + 1} \\ t_ {ij, \ eta} ^ {\ uparrow \ downarrow} &=t_ {2 (i-1) + 1,2j} \\ t_ {ij, \ eta} ^ {\ downarrow \ uparrow} &=t_ {2i, 2 (j-1) +1} \\ t_ {ij, \ eta} ^ {\ downarrow \ downarrow} &=t_ {2i, 2j}. \ end {array} $$ (6)
Aqui, \ (- Im \ Sigma _ {L, R} =- \ left (\ Sigma _ {L, R} ^ {r} - \ Sigma _ {L, R} ^ {a} \ right) / 2i \ ) são matrizes semidefinidas positivas com uma raiz quadrada de matriz bem definida, onde \ (\ Sigma _ {L, R} ^ {a} =\ left [\ Sigma _ {L, R} ^ {r} \ right] ^ { \ dag} \) são a autoenergia retardada / avançada do eletrodo esquerdo / direito. A submatriz 16 × 16 G r é a função retardada de Green, que conecta a primeira e a última supercélulas ao longo do x direção e pode ser calculado usando o método da função de Green recursiva. Os coeficientes de transmissão total do η vale são \ (T _ {\ eta} =T ^ {\ uparrow \ uparrow} _ {\ eta} + T ^ {\ uparrow \ downarrow} _ {\ eta} + T ^ {\ downarrow \ uparrow} _ {\ eta } + T ^ {\ downarrow \ downarrow} _ {\ eta} \), e a polarização do spin P s e polarização de vale P η pode ser dado por
$$ {\ begin {alinhados} P_ {s} &=\ frac {T_ {K} ^ {\ uparrow \ uparrow} + T_ {K} ^ {\ uparrow \ downarrow} -T_ {K} ^ {\ downarrow \ downarrow} -T_ {K} ^ {\ downarrow \ uparrow} + T_ {K '} ^ {\ uparrow \ uparrow} + T_ {K'} ^ {\ uparrow \ downarrow} -T_ {K '} ^ {\ downarrow \ downarrow} -T_ {K '} ^ {\ downarrow \ uparrow}} {T_ {K} + T_ {K ^ {\ prime}}}, \\ P _ {\ eta} &=\ frac {T_ {K} -T_ {K ^ {\ prime}}} {T_ {K} + T_ {K ^ {\ prime}}}. \ end {alinhado}} $$
Resultados e discussão
Nos cálculos dos coeficientes de transmissão dependentes de spin, definimos τ 2 = τ 1 = t =1 como a unidade de energia, a força SOC t então =0,005 t , e a energia de Fermi E f =1.001 t então , que está situado na parte inferior da banda de condução. A largura da região de dispersão é W =1000 para o defeito de linha única e uma largura adicional WR =1000 também é levada em consideração para os dois defeitos de linha paralela, como mostrado na Fig. 1a.
A Figura 2 representa os coeficientes de transmissão de spin conservado / spin-flip do vale \ (\ eta, T ^ {sc} _ {\ eta} / T ^ {sf} _ {\ eta} \), como uma função do incidente ângulos α (a) e da força RSOC t R (b – d). A Figura 2a – c corresponde ao caso do defeito de linha única e (d) é para o caso dos dois defeitos de linha paralela. É mostrado que em um t definido R (por exemplo, t R =5 t então como na Fig. 2a), os coeficientes de transmissão dependentes de spin \ (T ^ {sc} _ {K} / T ^ {sf} _ {K} \) são constantes e independentes dos ângulos incidentes devido à relação de dispersão parabólica , como mostrado na Fig. 2a. Portanto, nos seguintes cálculos, podemos usar o ângulo de incidência α =0 como exemplo. Para um fraco t R , um fenômeno oscilante semelhante ao de um gás de elétron bidimensional [26, 27] aparece devido à divisão de Rashba, como mostrado na inserção da Fig. 2b. Como t R aumenta ( t R > t então ), \ (T_ {K} ^ {\ uparrow \ uparrow} \) e \ (T_ {K} ^ {\ uparrow \ downarrow} \) têm a mesma periodicidade de oscilação e quase as mesmas magnitudes que t R que consiste em alguns picos e nadirs de oscilação, enquanto \ (T_ {K} ^ {\ downarrow \ downarrow} / T_ {K} ^ {\ downarrow \ uparrow} \) tende a zero porque a energia de Fermi está em sua lacuna, como mostrado na Fig. 2b. Assim, o coeficiente de transmissão total de K vale é principalmente contribuído pelo estado de spin up. Na verdade, as imagens de oscilação dos dois vales, K e K ′ , coincide enquanto os coeficientes de transmissão de K ′ vale é principalmente contribuído pelos elétrons spin-down.
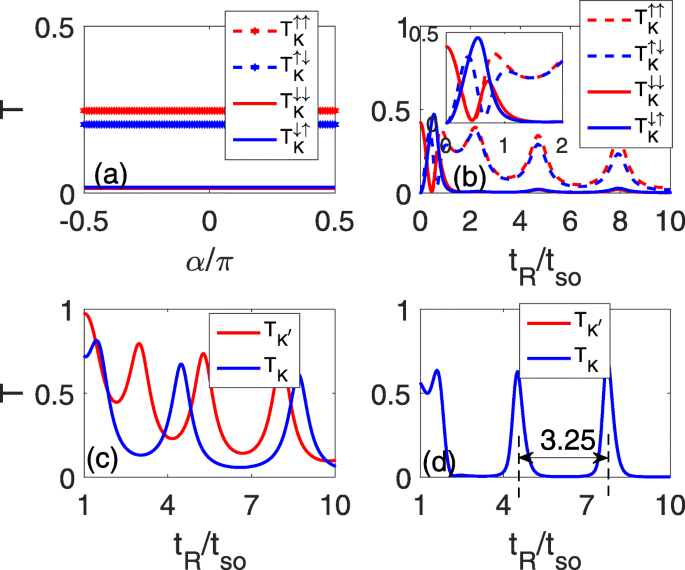
Coeficientes de transmissão spin-conservados e spin-flip como funções dos ângulos incidentes α em t R =5 t então em a e como funções da força RSOC t R em b - d , onde a - c são para o defeito de linha única e d é para os dois defeitos de linha paralela, com Δ z =0,2 t então em c
Na presença de um campo elétrico perpendicular, a degenerescência do vale é elevada, e os comportamentos oscilantes dos dois vales diferem:a periodicidade oscilante do K vale aumenta, enquanto o do K ′ o vale diminui, como mostrado na Fig. 2c. No entanto, parece inviável filtrar um estado de vale cônico com apenas um único defeito de linha porque os nadirs oscilantes têm uma magnitude definida. Naturalmente, pode-se considerar o fenômeno da oscilação com dois defeitos de linha paralela para restringir ainda mais a transmissão, como mostrado na Fig. 2d. A comparação da Fig. 2b com d revela que o pico da oscilação se torna estreito e agudo, enquanto o nadir da oscilação se amplia e enfraquece, o que forma a plataforma de transmissão zero. O espaço entre dois picos de oscilação vizinhos é fixado em 3,25 t então , conforme caracterizado pelas duas linhas tracejadas na Fig. 2d.
Para obter um melhor efeito de filtro de vale, concentramos nossa atenção no efeito do campo elétrico perpendicular. Os resultados deste efeito são mostrados na Fig. 3. Como discutido acima, a periodicidade de oscilação dos dois vales muda de maneira oposta, e os picos de oscilação sobrepostos originais na Fig. 2d são aliviados. Enquanto isso, o platô de transmissão zero se alarga e se estreita para T K e \ (T_ {K ^ {\ prime}} \), respectivamente, como mostrado na Fig. 3a e b. Em Δ z =0,15 t então , o espaço entre os dois picos de oscilação vizinhos desenvolve-se em 3,6 t então para T K , embora seja reduzido para 3,1 t então para \ (T_ {K ^ {\ prime}} \), como indicado pelas duas linhas tracejadas azuis e vermelhas mostradas na Fig. 3a. À medida que o campo elétrico se fortalece, o espaço entre os dois picos de oscilação vizinhos continua a aumentar / diminuir para T K / \ (T_ {K ^ {\ prime}} \), que é 5,4 t então /2.8t então em Δ z =0,3 t então , conforme mostrado na Fig. 3b. A mudança na periodicidade de oscilação levará às regiões correspondentes de amplo platô de pico zero, onde a polarização de vale perfeita com P η =± 1 platôs podem ser realizados, conforme mostrado nas Fig. 3c e d. Simultaneamente, é mostrado que a alta polarização de spin P s também surge quando P η =± 1.
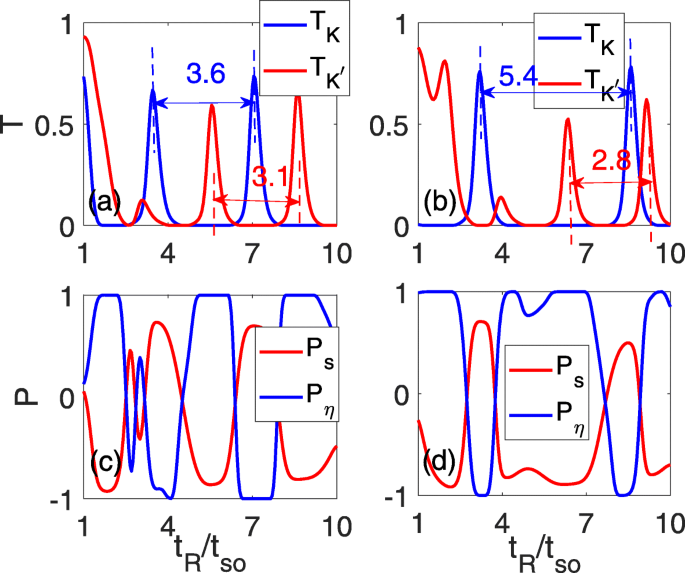
Os coeficientes de transmissão total \ (T_ {K} / T_ {K ^ {\ prime}} \) ( a , b ) e a polarização spin / vale ( c , d ) em função da força RSOC t R para diferentes potenciais de sub-rede. Δ z =0,15 t então em a e c e Δ z =0,3 t então em b e d ; os outros parâmetros são idênticos aos da Fig. 2d
No entanto, devido à incontrolabilidade do RSOC, ainda é difícil detectar tais correntes puras de vale experimentalmente, embora o RSOC induzido no defeito da linha possa ser maior do que o SOC intrínseco. Para convenientemente sondar experimentalmente a corrente de vale pura, também investigamos os coeficientes de transmissão e a polarização de vale como uma função do campo elétrico, que pode ser controlado continuamente durante um experimento. É mostrado que a polarização de vale perfeita com P η =± 1 pode emergir em um certo intervalo de Δ z e que pode mudar de P η =1 a P η =−1 conforme o campo elétrico aumenta, conforme mostrado na Fig. 4a. Para um t definitivo R (por exemplo t R =7,2 t então , conforme indicado com uma linha tracejada na Fig. 4a), os coeficientes de transmissão \ (T_ {K} / T_ {K ^ {\ prime}} \) oscilam com Δ z , onde os picos de ampla transmissão do K ( K ′ ) vale corresponde aos planaltos de transmissão zero do K ′ ( K ) vale. Os coeficientes de transmissão total são basicamente contribuídos por um vale conforme o campo elétrico varia, e a polarização de vale perfeita pode sempre ocorrer em torno do valor máximo de \ (T_ {K} / T_ {K ^ {\ prime}} \), como mostrado em Fig. 4b. Conforme a energia Fermi se afasta da borda da banda, a polarização de vale perfeita ainda pode sobreviver mesmo em E f =1,5 t então , onde a relação de platô pode ser bem mantida, conforme mostrado na Fig. 4c. Durante um experimento, pode-se analisar as correntes elétricas polarizadas de vale do chumbo da esquerda para a direita com uma quantidade mensurável experimentalmente, como a condutância, que é proporcional ao coeficiente de transmissão total. A condutância máxima entre dois valores mínimos (às vezes, eles são zero) deve ser de um vale. Podemos estimar a magnitude da condutância de acordo com a fórmula \ (G =\ frac {e ^ {2}} {h} \ int _ {- k_ {F}} ^ {k_ {F}} T \ frac {dk_ {y}} {2 \ pi / L_ {y}} =\ frac {e ^ {2}} {h} \ frac {Ly \ sqrt {E ^ {2} -t ^ {2} _ {so}} } {2 \ pi \ hbar v_ {F}} 2T \) [28], onde L y =2 a ≈7,72Å é a largura do defeito da linha de siliceno, v F =5,5 × 10 5 m / s é a velocidade de Fermi, \ (\ hbar =h / 2 \ pi \) é a constante de Planck reduzida com \ (\ phantom {\ dot {i} \!} h =4,13566743 \ times 10 ^ {- 15} eV \ cdot s, T =T_ {K} + T_ {K '} \) é o coeficiente de transmissão total e E é a energia local dos elétrons incidentes. Então, a condutância é cerca de \ (G \ approx \ left [0.7T \ sqrt {E ^ {2} -t ^ {2} _ {so}} / eV \ right] \ frac {e ^ {2}} { h} \). Também foi descoberto que conforme a energia no local no lado do incidente é elevada para E =0,15 t ( t =1,6 eV ), os coeficientes de transmissão dos dois vales mudam apenas um pouco em comparação com a Fig. 4c devido à conservação de spin e momento e a relação de platô de pico zero da transmissão se mantém, como mostrado na Fig. 4d. Neste caso, a condutância é de cerca de \ (G \ approx 0,17T \ frac {e ^ {2}} {h} \) que é considerável e pode ser detectada no experimento. A janela de energia para observar este fenômeno é de cerca de 0,5 t então ( t então < E <1,5 t então ) que é proporcional a t então . No experimento, não é difícil controlar a energia de Fermi perto da borda da banda e a lacuna SOC pode até ser radicalmente aumentada para 44 meV pela proximidade com a bicamada Bi (111) [29] que pode melhorar muito a região de energia para detectar o puro vale atual. Além disso, o modelo computacional também pode ser aplicável a outras contrapartes de grafeno, germaneno [30], estaneno e MoS 2 [31-36], que têm lacunas de banda ainda maiores [37, 38], bem como as forças do SOC (a força do SOC pode chegar a 0,1eV para o estaneno [38, 39]). Em um experimento real, é fácil perceber um RSOC forte que pode exceder o SOC intrínseco quebrando a simetria do espelho no plano com o substrato especial [40]. Portanto, este esquema pode ser totalmente viável em experimento.
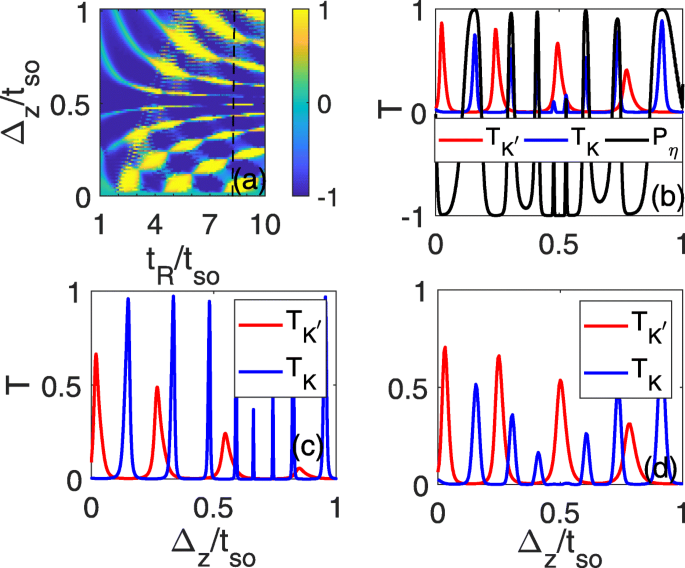
Polarização de vale a e \ (T_ {K} / T_ {K ^ {\ prime}} \) ( b - d ) como funções de Δ z e t R . t R =7,2 t então em ( b - d ), E f =1,5 t então em c e d , e a energia no local é E =0,15 t no eletrodo esquerdo em d ; todos os outros parâmetros são idênticos aos da Fig. 2d
Conclusões
Propusemos um método elétrico para gerar uma corrente polarizada em vale em defeitos de linha de siliceno. Em nítido contraste com as abordagens elétricas convencionais que são usadas para produzir corrente polarizada de vale, exploramos o RSOC, que é considerado o ajuste da polarização de spin amplamente usada em FETs com polarização de spin. Verifica-se que os coeficientes de transmissão dos dois vales oscilam com a mesma periodicidade e intensidade, que é composta por picos de transmissão e platôs de transmissão zero. A corrente polarizada de vale pode ser gerada sintonizando a periodicidade oscilante dos dois vales com um campo elétrico, que pode destruir a simetria dos estados de vale e ocasionar as correspondentes regiões de platô de pico zero de transmissão. Além disso, também fornecemos um esquema para detectar a corrente de vale pura em experimento e os resultados podem lançar luz sobre a manipulação de correntes polarizadas de vale por meios elétricos.
Disponibilidade de dados e materiais
Os conjuntos de dados gerados durante e / ou analisados durante o estudo atual estão disponíveis nos autores correspondentes mediante solicitação razoável.
Abreviações
- 2D:
-
Bidimensional
- ELD:
-
Defeito de linha estendida
- FET:
-
Transistor de efeito de campo
- RSOC:
-
Acoplamento rotação-órbita Rashba
- SOC:
-
Acoplamento spin-órbita intrínseco
Nanomateriais
- Medição de nível de fluido sem contato usando um chip refletômetro
- Como inicializar a RAM do arquivo usando TEXTIO
- Avançando para 7nm
- Usando ângulos para melhorar o futuro da eletrônica
- Concreto inteligente usando nanopartículas
- Tipos de dados C# com exemplo:Aprenda Int | Flutuar | Duplo | Caracteres
- Login no Facebook usando Python:Exemplo de login no FB
- Defeitos de Fundição:Tipos, Causas e Soluções
- Evitando problemas e defeitos de soldagem usando metais verificados
- 5 maneiras de baixo custo para começar a usar a automação industrial 4.0 para melhorias de linha



