Caracterização em escala atômica de deformação deslizante e usinabilidade nanométrica de cristal único 6H-SiC
Resumo
Como um importante material semicondutor de terceira geração, o mecanismo de microdeformação e remoção de 6H-SiC na escala atômica são vitais para a obtenção de superfície ultra-lisa e livre de danos com etapas atômicas. Devido às dificuldades em observar diretamente a superfície / subsuperfície da região de nanomáquina por meios experimentais atuais, o método de dinâmica molecular é usado para estudar os detalhes em escala atômica no processo de nanomáquina, como movimento de deslizamento de deslocamento, transição de fase e mecanismo de separação de material. A influência da anisotropia induzida por cristalografia na deformação por escorregamento e na usinabilidade nanométrica de 6H-SiC é investigada enfaticamente. Este estudo contribui significativamente para o entendimento do processo de microdeformação e nanomáquina do 6H-SiC.
Introdução
Como o material semicondutor de terceira geração com largo intervalo de banda, o SiC tem as características de alto campo de degradação, alta tolerância à radiação, alta velocidade de saturação de portador, condutividade térmica rápida, pequena constante dielétrica e propriedades químicas estáveis, por isso tem amplas aplicações nos campos de alta temperatura, alta frequência, alta potência, anti-radiação e dispositivos optoeletrônicos de comprimento de onda curto e integração optoeletrônica [1].
Os cristais de SiC mais amplamente usados são 3C, 4H e 6H. Métodos de processamento como retificação / lapidação / polimento ainda são os principais métodos durante a usinagem de SiC monocristalino. Porém, a relação de dureza entre diamante e SiC é próxima a 2:1 (profundidade de processamento <50 nm)), o que é muito inferior ao valor recomendado de 5:1 para o processo de usinagem [2]. Desgaste severo da ferramenta de corte e dano subsuperficial influenciam diretamente a qualidade do wafer. Para resolver esses problemas, muito trabalho foi feito para entender o comportamento de remoção do SiC em nanoescala. O mecanismo de remoção do 3C-SiC e a influência dos fatores de processamento têm sido amplamente estudados, como o mecanismo de deformação plástica durante o processo de corte [3,4,5,6,7], desgaste da ferramenta [8], comportamento de atrito [9 ], e anisotropia de 3C-SiC [10] e influência das temperaturas de corte [11].
6H-SiC tem uma estrutura de pilha ABCACB mais complexa. Embora o mecanismo de remoção de 6H-SiC no processamento SPDT (torneamento de diamante de ponta única) (como a influência do ângulo de ataque da ferramenta no processo de remoção de material [12] e transição frágil-dúctil [13]) seja estudado, a pesquisa é obviamente menos de 3C-SiC. O bandgap de 6H-SiC (3 eV) é obviamente maior do que o de 3C-SiC (2,3 eV). Atualmente, o nível tecnológico do processo de crescimento do bastão 6H-SiC é muito maior do que o do 3C-SiC. 6H-SiC é muito mais usado em aplicações industriais do que 3C-SiC. Dispositivos correspondentes foram aplicados em campos de alta frequência, alta potência e alta temperatura, como retificador Schottky, tiratron e MOSFET de potência (Metal-Oxide-Semiconductor Field-Effect Transistor). Para melhorar a qualidade da superfície / subsuperfície usinada de 6H-SiC, o meio mais eficiente e eficaz no momento é encontrar uma combinação apropriada de plano de cristal (superfície de usinagem) / orientação de cristal (direção de usinagem) que seja mais adequada para o processo de 6H -SiC.
Experimentos e simulações de scratch são alguns dos métodos mais comuns e eficazes para explorar o comportamento de remoção [14, 15]. A pesquisa sobre o mecanismo de remoção de material durante o processo de raspagem tem um grande significado orientador para o processo de usinagem abrasivo real. O método de dinâmica molecular pode fornecer formação de danos e processo de remoção em nanoescala. Portanto, a simulação de dinâmica molecular foi utilizada para analisar o comportamento de remoção do 6H-SiC sob a influência da anisotropia induzida por cristalografia.
Metodologia
As simulações de corte neste artigo foram concluídas usando simulador atômico / molecular maciçamente paralelo em grande escala (LAMMPS) [16]. OIVTO [17] e o método de identificação da estrutura do diamante [18] foram usados para visualização do modelo e identificação de defeitos neste estudo. As implementações de modelagem de peças e ferramentas dependiam do LAMMPS sem o auxílio de outro software. Conforme mostrado na Fig. 1a-c, a peça e a ferramenta foram definidas como corpos deformáveis e o comportamento do desgaste foi investigado durante a simulação. A ferramenta e o modelo da peça de trabalho foram divididos em três partes:uma camada atômica limite, uma camada atômica termostática e uma zona de átomos newtonianos. A fim de manter a peça de trabalho na posição inicial, os átomos da camada limite na extremidade inferior e direita da peça de trabalho foram fixados. Os átomos na camada do termostato e na camada Newtoniana seguem a segunda lei de Newton. Um limite periódico foi aplicado ao longo de y direção. Antes da simulação de scratch, os modelos foram relaxados por NVE ensemble com método de termostato de Berendsen. Um período de relaxamento de 50 ps foi aplicado antes das simulações de arranhões para obter um estado de energia estável. A forma abrasiva é uma pirâmide triangular de coroa esférica com ângulo de ponta a ponta de 90 °. Como mostrado na Fig. 2, os planos de cristal comuns (plano a (plano basal), plano m (plano prismático) e plano c) para 6H-SiC foram selecionados como as superfícies de usinagem. Considerando a simetria da estrutura, as seguintes combinações de plano / orientação foram selecionadas como superfície de usinagem / direção de usinagem:\ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline { 1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \). Os parâmetros de processamento da simulação são mostrados na Tabela 1. Antes da simulação de arranhão, os abrasivos foram colocados no lado esquerdo da peça de trabalho e a ponta do abrasivo está 50 Å abaixo da superfície superior da peça de trabalho. A distância mais próxima entre os abrasivos e a peça de trabalho é 30 Å, que está longe da faixa de corte do potencial de interação. O abrasivo se move da extremidade livre da peça de trabalho na direção positiva de x -eixo e conclua o processo de raspagem.
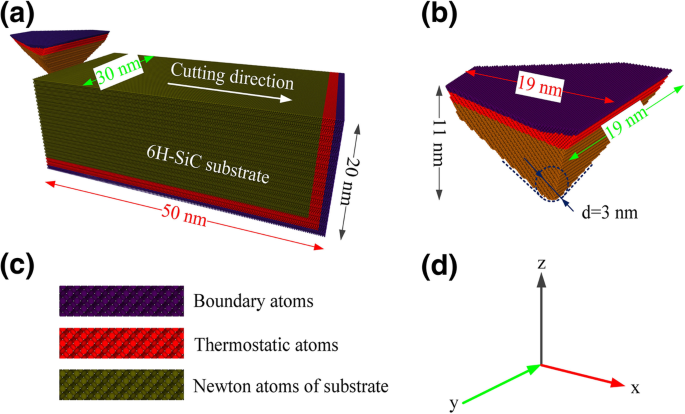
a Modelo MD de simulação de nanoscratching. b A morfologia da ferramenta. c Estrutura do modelo. d Direção do eixo
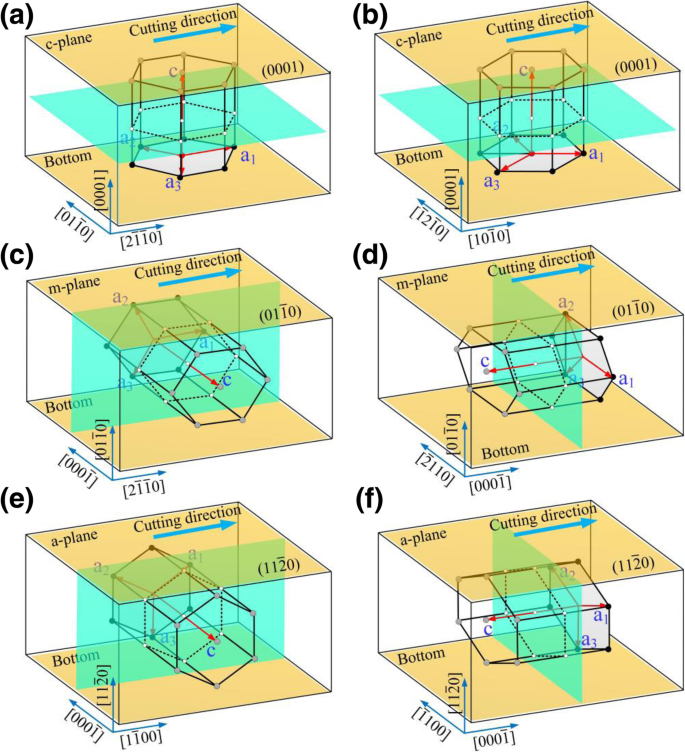
Diagrama esquemático do processo de arranhar, onde a - f são os modos de processo correspondentes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ direita) / \ esquerda [0001 \ direita] \), \ (\ esquerda (11 \ overline {2} 0 \ direita) / \ esquerda [1 \ overline {1} 00 \ direita] \), e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente
A função potencial atômico desempenha um papel crucial na precisão e confiabilidade da simulação de dinâmica molecular. De acordo com os testes e simulações anteriores para as propriedades mecânicas e mecanismos de remoção do SiC monocristalino, a função de potencial analítico de ordem de ligação (ABOP) proposta por Erhart e Albe [19] é mais adequada para interações de silício e carbono. Os parâmetros usados na função potencial são mostrados na Tabela 2 [19]. Em vez da função de energia potencial Tersoff [6], a função potencial ABOP é usada para definir as interações Si-Si, CC e Si-C dentro e entre a ferramenta e a peça durante o processamento [2, 7, 8, 10, 11].
Resultados e discussão
Análise de Maquinabilidade Nanométrica
Conforme mostrado nas Figs. 3 e 4, a anisotropia de 6H-SiC teve um impacto significativo na usinabilidade nanométrica (profundidade usinada, modo de remoção, quantidade de remoção e profundidade de dano subsuperficial (SSD), etc.). De acordo com a relação entre a superfície de usinagem / direção de usinagem e o plano basal / c -eixo (ver Fig. 3), os modos de processamento de material podem ser divididos em três categorias:(i) o plano basal é selecionado como a superfície de usinagem, (ii) o plano basal é perpendicular à superfície de usinagem e c -eixo é perpendicular à direção de usinagem, e (iii) o c -eixo é paralelo à direção de usinagem.
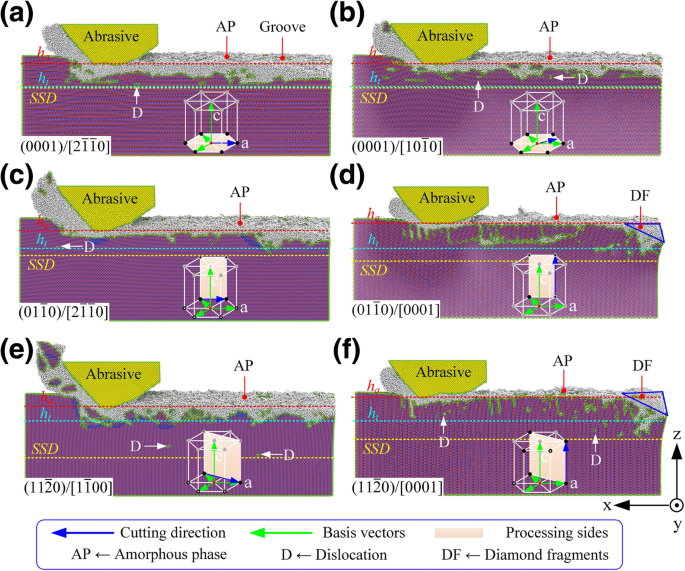
Topografia da superfície usinada sob diferentes condições de plano / orientação de cristal, onde a - f são os modos de processo correspondentes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ direita) / \ esquerda [0001 \ direita] \), \ (\ esquerda (11 \ overline {2} 0 \ direita) / \ esquerda [1 \ overline {1} 00 \ direita] \), e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente
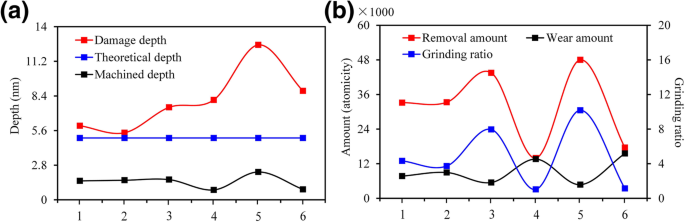
Usinabilidade nanométrica sob diferentes condições de plano / orientação do cristal, a a influência da anisotropia na profundidade usinada e na profundidade do dano, b a influência da anisotropia na quantidade de remoção, quantidade de desgaste e taxa de retificação. 1, 2, 3, 4, 5 e 6 são os métodos de processo correspondentes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \), \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente. A profundidade da camada de dano se refere à profundidade máxima dos defeitos internos do cristal causados pelo arranhão. A profundidade teórica se refere à profundidade predefinida antes do processamento. A profundidade usinada refere-se à profundidade residual após o arranhão. A quantidade de remoção refere-se ao número de átomos dos quais o material da peça de trabalho é removido. A quantidade de desgaste refere-se à diferença no número de átomos dos grãos abrasivos antes e depois do arranhão
(i) Conforme mostrado na Fig. 3a, b, a usinabilidade nanométrica de 6H-SiC foi extremamente semelhante quando o modo de processamento foi selecionado como \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). No entanto, o processo de remoção de 6H-SiC foi mais inclinado para o modo frágil quando o modo de processamento foi selecionado como \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). (ii) Conforme mostrado na Fig. 3c, e, quando os modos de processamento foram selecionados como \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), a profundidade usinada e a quantidade de remoção de material foram significativamente maiores do que aquelas nos outros métodos de processamento. Conforme mostrado na Fig. 4, sob a mesma profundidade teórica de processamento ( h t =5,0 nm), a taxa de remoção de material no modo de processamento \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) foi 3,4 vezes maior que que está no modo de processamento \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \). A taxa de processamento de material (quantidade de remoção de material / desgaste da ferramenta) foi de 10,1, mas o SSD sob este parâmetro de processamento também foi muito maior do que sob outras condições de processamento, atingindo 2,3 vezes de \ ((0001) / \ left [10 \ overline { 1} 0 \ right] \). Havia um grande número de nanocristalitos nas superfícies usinadas e nos chips. Um grande número de falhas frágeis ocorreu sob esta condição. O modo de processamento \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) é adequado apenas para processamento nanogroove que requer alta eficiência de processamento, mas é insensível ao danos subterrâneos. A taxa de remoção de material de \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) foi semelhante à de \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) mas o SSD era apenas 50% do último. Além disso, a espessura da camada amorfa na superfície usinada era muito menor do que \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ ((0001) / \ left [10 \ overline {1} 0 \ right] \). A distribuição da fase subsuperficial era uniforme e as propriedades mecânicas de todo o sulco eram melhores do que nos outros métodos de processamento. Portanto, o modo de processamento \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) é a melhor escolha para o processamento de micro-nano ranhuras na superfície 6H-SiC com alta eficiência , alta precisão e baixo SSD. (iii) Como mostrado nas Figs. 3d, f, quando a direção de usinagem era paralela a c -eixo, a ponta foi severamente desgastada durante o estágio inicial de processamento. Embora a profundidade usinada e a taxa de remoção de material fossem muito menores do que aquelas nos outros métodos de processamento e a taxa de processamento de material fosse apenas cerca de 1,0, o SSD de \ (\ left (01 \ overline {1} 0 \ right) / \ left [ 0001 \ right] \) e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) os modos de processamento eram mais do que \ (\ left (01 \ overline {1} 0 \ direita) / \ esquerda [2 \ overline {1} \ overline {1} 0 \ direita] \). Portanto, não é recomendado empregar \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) no processamento de ranhuras micro-nano na superfície de 6H-SiC. No entanto, esses modos demonstram uma excelente resistência ao desgaste; portanto, eles estão aptos para a face de inclinação da ferramenta de corte de SiC monocristalino, que tem amplas perspectivas no campo de processamento de ultraprecisão de metais ferrosos.
Análise do movimento labial e distribuição de danos à superfície
Distribuição dos fatores de Schmid no processo de arranhão com base em uma ponta de pirâmide triangular
Os sistemas de deslizamento comuns do sistema de cristal hexagonal (ver Fig. 4) incluem principalmente deslizamento basal, deslizamento prismático e deslizamento piramidal. A resistência ao escorregamento está relacionada à energia de falha de empilhamento generalizada (GSF) e d E GSF / d x vs. ( x / b ) dos sistemas de deslizamento. O movimento de deslizamento ocorreria no plano mais denso e ao longo da direção mais curta [10]. Os sistemas de deslizamento preferencial no deslizamento basal são deslizamento basal (conjuntos aleatórios) / <\ (1 \ overline {1} 00 \)> e deslizamento basal (conjuntos aleatórios) / <\ (11 \ overline {2} 0 \)> [20]. Como o primeiro carece de um mínimo de energia intermediário, o último tem precedência nas simulações e experimentos [20]. Portanto, os movimentos de deslizamento considerados neste trabalho são os seguintes:deslizamento basal (conjuntos aleatórios) / <\ (11 \ overline {2} 0 \)> e deslizamento e
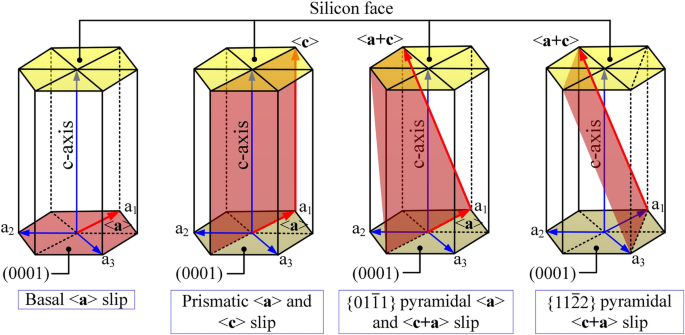
Sistemas de deslizamento do sistema hexagonal
O componente de tensão de cisalhamento no plano de deslizamento τ ss pode ser calculado pela relação:
$$ {\ tau} _ {\ mathrm {ss}} ={\ sigma} _ {\ mathrm {cont}} \ mathit {\ cos} <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {n_g}> \ cos <\ overset {\ rightharpoonup} {f}, \ overset {\ rightharpoonup} {t_g}> ={\ sigma} _ {\ mathrm {cont}} \ bullet m $$ (1)
onde σ cont é a tensão de contato, \ (\ overset {\ rightharpoonup} {f} \) é direção de carregamento, \ (\ overset {\ rightharpoonup} {n_g} \) e \ (\ overset {\ rightharpoonup} {t_g} \) são o plano de deslizamento normal e direção de deslizamento no sistema de coordenadas cartesianas globais, e m é o fator Schmid. O sistema de coordenadas global foi fixado e o sistema de coordenadas local girado com a direção do cristal. O x -eixo do sistema de coordenadas local era paralelo ao vetor básico \ (\ overset {\ rightharpoonup} {a_1} \) enquanto o z -eixo era paralelo ao vetor básico \ (\ overset {\ rightharpoonup} {c} \).
Durante o processo de raspagem, a face de contato principal da ponta da pirâmide triangular foi a face de inclinação, mas quando a ferramenta se desgastou severamente, a face de contato principal transitou para o composto da face de inclinação e o topo da ponta. A direção de carregamento correspondente \ (\ overset {\ rightharpoonup} {f} \) é apresentada como
$$ \ left \ {\ begin {array} {c} \ overset {\ rightharpoonup} {f_1} =\ left ({f} _ {1x}, {f} _ {1y}, {f} _ {1z} \ right) \ kern8em \ mathrm {rake} \ \ mathrm {face} \ \\ {} \ overset {\ rightharpoonup} {f_2} =\ left ({f} _ {2x}, {f} _ {2y}, {f} _ {2z} \ right) \ kern9.75em \ mathrm {tip} \ \ mathrm {top} \ end {array} \ right. $$ (2)
onde \ (\ overset {\ rightharpoonup} {f_1} =\ left (1,0, - \ sqrt {2} \ right) \), \ (\ overset {\ rightharpoonup} {f_2} =\ left (0,0 , -1 \ right) \) no sistema de coordenadas global.
Como um sistema de cristal hexagonal, o sistema de deslizamento de 6H-SiC pode ser expresso como { h k i l } / < u v t w >. O plano de deslizamento normal \ (\ overset {\ rightharpoonup} {n_c} \) e direção de deslizamento \ (\ overset {\ rightharpoonup} {t_c} \) no sistema de coordenadas cartesianas local são mostrados como
$$ \ overset {\ rightharpoonup} {n_c} =\ left (\ frac {3} {2} h, \ frac {\ sqrt {3}} {2} \ left (h + 2k \ right), \ frac { 3 la} {2c} \ right) $$ (3) $$ \ overset {\ rightharpoonup} {t_c} =\ left (u- \ frac {1} {2} \ left (v + t \ right), \ frac {\ sqrt {3}} {2} \ left (vt \ right), \ frac {c} {a} w \ right) $$ (4)
O plano de deslizamento normal \ (\ overset {\ rightharpoonup} {n_g} \) e direção de deslizamento \ (\ overset {\ rightharpoonup} {t_g} \) no sistema de coordenadas cartesianas global são mostrados como
$$ \ overset {\ rightharpoonup} {n_g} =T \ bullet \ overset {\ rightharpoonup} {n_c} $$ (4) $$ \ overset {\ rightharpoonup} {t_g} =T \ overset {\ rightharpoonup} {\ marcador {t} _c} $$ (5)
onde a matriz de rotação forma do sistema de coordenadas global para o sistema de coordenadas local e os ângulos de rotação correspondentes são mostrados na Tabela 3
De acordo com as fórmulas (1) - (5), os fatores de Schmid dos sistemas de deslizamento correspondentes quando as direções de carregamento eram \ (\ overset {\ rightharpoonup} {f_1} \) e \ (\ overset {\ rightharpoonup} {f_2} \ ) são mostrados na Tabela 4. (i) O valor c / a de 6H-SiC atingiu 4,901, que é muito maior do que 1,633. Portanto, a tensão de cisalhamento crítica necessária para o escorregamento basal foi menor do que para o sistema de escorregamento prismático. Quando a superfície usinada era um plano basal, o coeficiente do sistema de escorregamento basal era maior do que os outros sistemas de escorregamento. Portanto, quando os modos de processamento foram selecionados como \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ ((0001) / \ left [10 \ overline {1 } 0 \ right] \), o movimento de deslizamento basal ocorreu primeiro. (ii) Quando os modos de processamento foram selecionados como \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ (\ esquerda (11 \ overline {2} 0 \ direita) / \ esquerda [1 \ overline {1} 00 \ direita] \), considerando apenas as direções de carregamento \ (\ overset {\ rightharpoonup} {f_1} \) e \ ( \ overset {\ rightharpoonup} {f_2} \), era teoricamente impossível para o deslizamento basal ocorrer, e o movimento de deslizamento prismático teve precedência. (iii) Quando os modos de processamento foram selecionados como \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) e \ (\ left (11 \ overline {2} 0 \ right ) / \ left [0001 \ right] \), como mostrado na Fig. 4, o tip-top foi seriamente usado durante o estágio de processamento inicial e \ (\ overset {\ rightharpoonup} {f_2} \) desempenhou um papel crucial em o processo de coçar. Portanto, o movimento de deslizamento ocorreria no sistema de deslizamento prismático simetricamente distribuído com o plano YOZ nas coordenadas globais.
Distribuição de danos à superfície / subsuperfície
Conforme mostrado na Fig. 6a, b quando \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e \ ((0001) / \ left [01 \ overline {1 } 0 \ right] \) foram selecionados, o movimento de deslizamento ocorreu principalmente no sistema de deslizamento \ ((0001) / <1 \ overline {2} 10> \), que é devido ao empurrar para frente da ferramenta. O modo de movimento deslizante correspondente é consistente com os resultados do cálculo do coeficiente de Schmidt. Havia grãos nanocristalinos e deflexões de rede na área de subsuperfície e esses danos formaram algumas zonas de distorção de rede irregulares. A fase amorfa cobriu toda a superfície usinada e a profundidade do deslocamento foi próxima à profundidade da camada de distorção da rede.
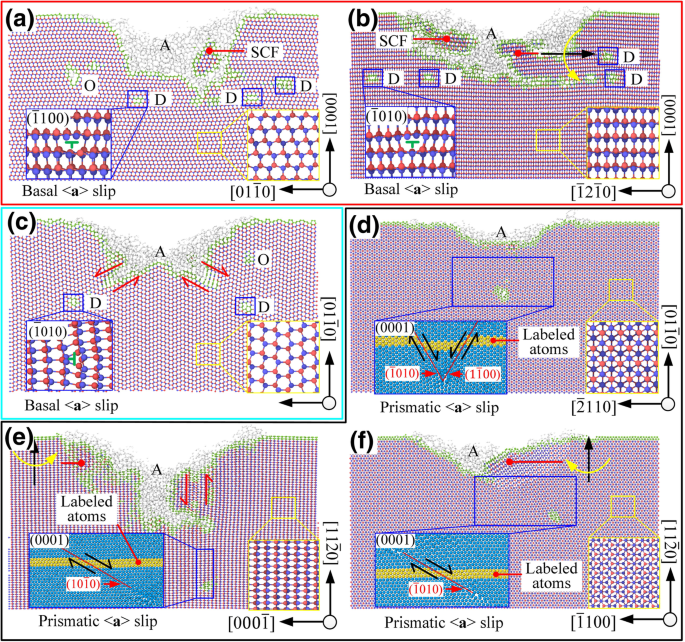
A seção transversal da área usinada, D é deslocamento, A é a fase amorfa, SCF é a forma de cristal único, O é outro tipo de defeito, onde a - f são os modos de processo correspondentes \ ((0001) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ ((0001) / \ left [10 \ overline {1} 0 \ right ] \), \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \), \ (\ left (01 \ overline { 1} 0 \ direita) / \ esquerda [0001 \ direita] \), \ (\ esquerda (11 \ overline {2} 0 \ direita) / \ esquerda [1 \ overline {1} 00 \ direita] \), e \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \), respectivamente.
Quando \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) é selecionado, como o coeficiente de Schmidt de basal < a > deslizamento é igual a 0, o < a basal> o escorregamento não deveria ocorrer em teoria. Mas o ângulo entre a direção de carregamento \ (\ overset {\ rightharpoonup} {f_1} \) e a direção de deslizamento \ (\ left [11 \ overline {2} 0 \ right] \) foi de apenas 5,3 °. Sob a ação de cisalhamento devido ao movimento relativo entre a área de contato e a área sem contato (ver Fig. 6c), o < a basal> deslizamento foi acionado antes do deslizamento prismático sob o modo de processamento de \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) e ocorreu em ambos os lados da ranhura em V. No modo de processamento de \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \), os ângulos entre a direção de carregamento \ (\ overset {\ rightharpoonup } {f_1} \) e as direções deslizantes \ (\ left [1 \ overline {2} 10 \ right] \) e \ (\ left [\ overline {1} \ overline {1} 20 \ right] \) eram 24,7 ° e 35,3 °, respectivamente. A ação de cisalhamento não induziu movimento de deslizamento do plano basal. O modo de movimento deslizante correspondente é consistente com os resultados do cálculo do coeficiente de Schmidt. Conforme mostrado na Fig. 6e, quando \ (\ left (11 \ overline {2} 0 \ right) / \ left [1 \ overline {1} 00 \ right] \) foi selecionado, o sistema de deslizamento \ (\ left [ 1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) teve um alto coeficiente de Schmidt sob a ação conjunta de \ (\ overset {\ rightharpoonup} {f_1} \) e \ (\ overset {\ rightharpoonup} {f_2} \), o que inevitavelmente resultaria em uma grande profundidade da camada de dano subsuperficial. A distorção da rede e a fase amorfa também existiam, mas ao contrário da usinagem no plano basal, a profundidade de deslocamento era significativamente maior do que a distorção da rede. O sp 3 → sp 2 o comportamento de transição ocorreu na região subsuperficial.
Quando a direção do processamento era paralela ao c -eixo, devido ao desgaste severo da ponta, o deslizamento prismático causado pela extrusão para baixo foi o modo de movimento de deslizamento primário no estágio de arranhão estável. O modo de movimento deslizante correspondente foi consistente com os resultados do cálculo do coeficiente de Schmidt. Quando \ (\ left (01 \ overline {1} 0 \ right) / \ left [0001 \ right] \) foi selecionado, com a direção de carregamento \ (\ overset {\ rightharpoonup} {f_2} \), os sistemas de deslizamento \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) e \ (\ left [\ overline {1} \ overline {1} 20 \ right] / \ left (1 \ overline {1} 00 \ right) \) tinha o mesmo coeficiente de Schmidt, deslizamento cruzado ocorreu nas duas superfícies de deslizamento com um ângulo de 60 °, e então, ocorreu o efeito de fixação que impediu o movimento de deslizamento . Assim, a profundidade máxima de dano subsuperficial SSD máximo seria menor ou igual a h t tan θ / 2 berço α / 2, onde θ =101 ° é o ângulo teórico do nanogroove e α =60 ° é o ângulo entre o plano de deslizamento \ (\ left (\ overline {1} 010 \ right) \) e \ (\ left (1 \ overline {1} 00 \ direita) \). Quando \ (\ left (11 \ overline {2} 0 \ right) / \ left [0001 \ right] \) foi selecionado, os sistemas de deslizamento \ (\ left [\ overline {2} 110 \ right] / \ left ( 0 \ overline {1} 10 \ right) \) e \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) também tiveram o mesmo coeficiente de Schmidt, mas o movimento de deslizamento foi afetado pelo desgaste irregular da ponta e apenas o sistema de deslizamento \ (\ left [1 \ overline {2} 10 \ right] / \ left (\ overline {1} 010 \ right) \) ocorreu.
Em resumo, como mostrado na Fig. 7, os danos nas regiões de subsuperfície sob diferentes condições de processamento foram principalmente deslocamentos, distorção de rede (torção / deslizamento relativo) e fase amorfa. A deformação de 6H-SiC foi causada principalmente pelo movimento de deslizamento, não cristalização de materiais e distorção de rede irregular. Os principais modos de deformação por escorregamento foram o escorregamento basal e o escorregamento prismático, que estão intimamente relacionados com a superfície / direção de processamento.
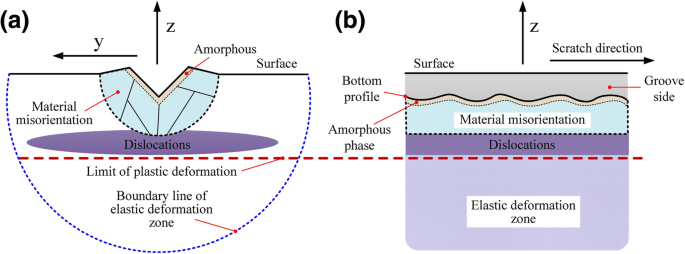
Distribuição de forma de dano superficial / subsuperficial processada. a xy corte transversal. b xz corte transversal
Observações finais
Neste trabalho, o mecanismo de deformação e a usinabilidade nanométrica de 6H-SiC foram investigados sob diferentes combinações de plano do cristal (superfície de usinagem) / orientação do cristal (direção de usinagem) e as seguintes conclusões são tiradas:
- (1)
O mecanismo de deformação de 6H-SiC durante o processo de arranhão em nanoescala é principalmente o resultado da combinação de transição de fase amorfa, distorção de rede e movimento de deslizamento de deslocamento. A profundidade da linha de deslocamento determina a profundidade do dano subsuperficial na área usinada de 6H-SiC.
- (2)
Basal < a > deslizamento e prismático < a > o movimento de deslizamento desempenha um papel dominante na deformação de deslizamento de 6H-SiC durante o processo de raspagem. Além do plano prismático modo de processamento / < a >, o movimento de deslizamento durante o processo de raspagem de 6H-SiC pode ser previsto por meio do algoritmo de Schmidt.
- (3)
O modo de processamento \ (\ left (01 \ overline {1} 0 \ right) / \ left [2 \ overline {1} \ overline {1} 0 \ right] \) é propício para alcançar uma alta taxa de remoção e baixo abrasivo desgaste, que é apto para a usinagem da superfície 6H-SiC. O plano basal e c -eixo são as faces e direções difíceis de usinar de 6H-SiC, que podem ser usadas como referência para o projeto de ferramentas de corte.
Disponibilidade de dados e materiais
Todos os dados gerados ou analisados durante este estudo estão incluídos neste artigo.
Abreviações
- A :
-
Fase amorfa
- ABOP:
-
Potencial analítico de pedido de ligação
- D :
-
Luxação
- d :
-
Espessura de cavaco indeformada
- GSF:
-
Energia de falha de empilhamento generalizada
- LAMMPS:
-
Simulador atômico / molecular maciçamente paralelo em larga escala
- MD:
-
Dinâmica Molecular
- MOSFET:
-
Transistor de efeito de campo semicondutor de óxido metálico
- NVE:
-
Número, volume e energia
- O :
-
Outro tipo de defeito
- SCF:
-
Forma de cristal único
- SPDT:
-
Torneamento de diamante de ponta única
- SSD:
-
Profundidade de dano subterrâneo
- SSD max :
-
Profundidade máxima de dano subterrâneo
Nanomateriais
- Rebarbação e rebarbação criogênica
- Fabricação e caracterização de Nano-Clips de ZnO pelo processo mediado por poliol
- Desenvolvimento e caracterização de compostos de cerâmica de vidro contendo Sr com base em hidroxiapatita biogênica
- O que é Metalurgia do Pó? - Definição e Processo
- O que é usinagem química? - Trabalho e processo
- O que é usinagem ultrassônica? - Trabalho e processo
- O que é soldagem por pulverização? - Processo e técnicas
- Significado e Tipos do Processo de Fabricação
- Serviços de retificação de superfície:processo e precisão
- Processo de Laminação a Quente e Frio



