Nanotubos de Grafeno HOT e HOT Grafeno:Novos Semimetais e Semicondutores de Dimensão Baixa

Resumo

Relatamos um novo alótropo de grafeno chamado HOT grafeno contendo hexágonos, octógonos e tetrágonos de carbono. Uma série correspondente de nanotubos também é construída enrolando o HOT folha de grafeno. Cálculos ab initio são realizados em estruturas geométricas e eletrônicas do HOT grafeno e o QUENTE nanotubos de grafeno. Cone de Dirac e alta velocidade de Fermi são alcançados em uma estrutura não hexagonal de QUENTE grafeno, o que implica que a estrutura em favo de mel não é uma condição indispensável para a existência de férmions de Dirac. QUENTE nanotubos de grafeno mostram estruturas eletrônicas distintas dependendo de sua topologia. O (0,1) n ( n ≥ 3) QUENTE os nanotubos de grafeno revelam as características dos semimetais, enquanto o outro conjunto de nanotubos (1,0) n mostra intervalos de banda continuamente ajustáveis (0 ~ 0,51 eV) com o tamanho do tubo. Uma competição entre o efeito de curvatura e a aproximação de dobramento de zona determina as lacunas de (1,0) n nanotubos. A nova conversão entre semimetalicidade e semicondutividade surge em tubos ultra-pequenos (raio <4 Å, ou seja, n <3).

Introdução

Por causa de sua flexibilidade de ligação, os sistemas baseados em carbono mostram um número ilimitado de estruturas diferentes com uma variedade igualmente grande de propriedades físicas. Essas propriedades físicas são, em grande parte, decorrentes da dimensionalidade dessas estruturas [1]. O grafeno é uma única camada bidimensional de átomos de carbono ligados em uma estrutura de rede hexagonal [2] revelando uma série de propriedades únicas, como portadores sem massa, alta velocidade de Fermi [3] e cones de Dirac [4, 5], que são característica de férmions de Dirac bidimensionais. A rede em favo de mel consistindo de duas sub-redes de carbono equivalentes desempenha um papel crucial na formação de tais propriedades intrigantes [2]. Enyashin e Ivanovskii [6] construíram 12 redes artificiais de carbono 2D, mas não encontraram nenhuma estrutura diferente do alótropo grafino que exibe o comportamento eletrônico semelhante ao grafeno. Parece implicar que os férmions semelhantes a Dirac em sp ² os sistemas de carbono ligado são dependentes da estrutura em favo de mel. Na dimensão inferior, o nanotubo de carbono é uma estrutura em favo de mel enrolada em um cilindro oco com diâmetro nanométrico e comprimento μm [7,8,9,10]. Como existe um número infinito de maneiras de enrolar uma folha em um cilindro, a grande variedade de geometrias helicoidais possíveis, definindo a quiralidade do tubo, fornece uma família de nanotubos com diferentes diâmetros e estruturas microscópicas [11,12,13]. As propriedades eletrônicas e de transporte estão certamente entre as propriedades físicas mais significativas dos nanotubos de carbono, e dependem crucialmente do diâmetro e da quiralidade [14,15,16,17,18]. Nanotubos de grafeno podem ser semimetálicos [14] ou semicondutores [19,20,21], com um gap variando de zero a alguns décimos de eV, dependendo de seu diâmetro e quiralidade [10, 14, 16]. Além disso, pode-se mostrar que o gap de banda de tubos semicondutores está simplesmente relacionado ao diâmetro do tubo. Os nanotubos semimetálicos também mantêm as propriedades únicas do grafeno, como portadores sem massa, alta velocidade de Fermi [22] e cones de Dirac [23]. Esses resultados notáveis podem ser obtidos a partir de uma variedade de considerações, começando da chamada abordagem de dobramento de banda, com base no conhecimento das propriedades eletrônicas da folha de grafeno, para o estudo direto de nanotubos usando abordagens semi-empíricas de ligação rígida [14, 16, 18, 23]. Comparando com cálculos ab initio mais sofisticados e resultados experimentais disponíveis, considerações mais refinadas, como efeitos de curvatura, k _F deslocamento [24, 25], hibridização σ-π [26] são introduzidos. Grafeno e materiais semelhantes ao grafeno [6] são considerados um material revolucionário para a geração futura de dispositivos eletrônicos de alta velocidade, lógicos de radiofrequência [27, 28], compósitos reforçados termicamente e eletricamente condutores [29, 30], catalisador [31], sensores [32,33,34,35], eletrodos transparentes [27, 36], etc. com base nas propriedades incomuns acima. Nas últimas décadas, os nanotubos de carbono também mostraram grande potencial em circuitos lógicos, armazenamento de gás, catálise e armazenamento de energia devido às suas extraordinárias propriedades eletrônicas, mecânicas e estruturais [37,38,39]. Portanto, a criação de novos alótropos de carbono (incluindo 2D e 1D) tem sido o foco de inúmeras explorações teóricas e experimentais devido à sua importância científica e tecnológica fundamental [40]. Porém, esclarecer completamente as estruturas dessas excitantes fases do carbono por meio de tecnologias experimentais atuais costuma ser irreal devido à sua quantidade limitada, assim como à mistura de outras fases. A previsão teórica é necessária e tem rendido grande sucesso [31,32,33,34,35, 40,41,42].

Neste estudo, projetamos um novo alótropo de grafeno que possui férmions de Dirac bidimensionais sem uma estrutura exclusivamente hexagonal. O novo alótropo foi construído com hexágonos, octógonos e tetrágonos de carbono entrelaçados e foi denominado QUENTE grafeno. QUENTE nanotubos de grafeno também foram construídos enrolando QUENTE folha de grafeno junto com diferentes direções. A propriedade eletrônica, efeito de curvatura, k _F efeito de deslocamento, etc. de QUENTE grafeno e nanotubos foram calculados usando cálculos ab initio com base na teoria da função de densidade (DFT).

Método de cálculo

Os cálculos atuais em HOT grafeno e QUENTE nanotubos de grafeno foram realizados usando um método de primeiros princípios baseado na teoria do funcional da densidade (DFT) com a aproximação do gradiente generalizado (GGA) na forma do funcional de correlação de troca de Perdew-Burke-Ernzerh (PBE) [43], como implementado no Ab initio Simulation Package de Viena (VASP) [44, 45]. As funções de onda foram expandidas em ondas planas até um corte de energia cinética de onda plana de 520 eV. As integrais da zona de Brillouin (BZ) foram realizadas usando um esquema de amostragem Monkhorst-Pack [46] com um k resolução de malha de pontos de 2π × 0,03 Å ^{- 1} . Os vetores de base da célula unitária (representando a forma e o tamanho da célula unitária) e as coordenadas atômicas foram totalmente relaxadas em cada sistema até que as forças em todos os átomos fossem menores do que 0,01 eV / Å.

Resultados e discussão

Estruturas geométricas e eletrônicas de HOT Grafeno

A estrutura geométrica de HOT O grafeno (Fig. 1a) mostra uma situação de ligação mais complicada do que o grafeno. A variedade de polígonos de carbono em QUENTE o grafeno resulta em vários caracteres de ligação de carbono. Esses polígonos em QUENTES o grafeno compartilha arestas comuns entre si, e as ligações podem ser distinguidas pelos dois polígonos aos quais pertencem. Portanto, em nossa pesquisa, eles são nomeados como 6–8 ligações, 4–8 ligações, 4–6 ligações, 6–6 ligações e 8–8 ligações. As ligações 4–8 e 6–8 têm dois comprimentos de ligação diferentes:1,44 Å e 1,47 Å para ligações 4–8; 1,41 Å e 1,48 Å para 6–8 ligações. As ligações 4–6, 6–6 ligações e 8–8 ligações têm comprimentos de ligação exclusivos de 1,44 Å, 1,46 Å e 1,34 Å, relativamente. A Figura 1b mostra a estrutura de banda e densidade de estados (DOS) de HOT grafeno com o BZ correspondente representado na Fig. 1c. O ponto de cruzamento das bandas de energia no nível de Fermi indica semimetalicidade de QUENTE grafeno, o que é confirmado pelo desaparecimento do DOS no nível de Fermi. O ponto de Dirac está localizado em (0, 0,0585, 0) adjacente a Γ. A estrutura da banda 3D (Fig. 2) apresenta as superfícies da banda próximas ao nível de Fermi, onde se podem ver os cones de Dirac formados pelas superfícies cônicas superior e inferior que se encontram em dois pontos de Dirac exatamente na superfície de Fermi. A velocidade de Fermi correspondente (v _F ) dos férmions de Dirac, avaliados a partir do gradiente das dispersões lineares das estruturas de banda, é 6,27 × 10 ⁵ m / s, que é um pouco menor que 8,1 × 10 ⁵ m / s [22] para nanotubo de grafeno e 8,6 × 10 ⁵ m / s [47, 48] para grafeno. O alto v _F implica alta mobilidade das operadoras no HOT grafeno.

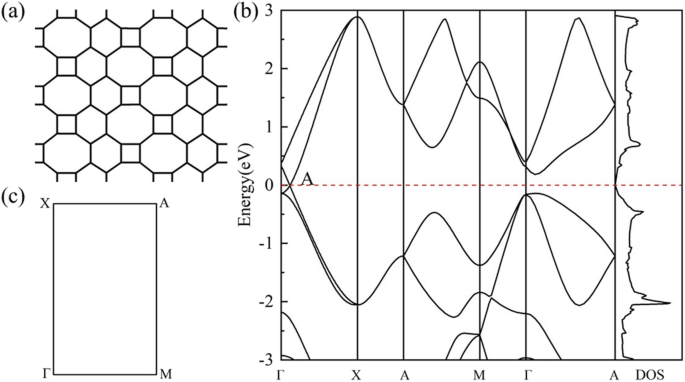
( a ) Geometria de HOT grafeno; ( b ) Estruturas de banda e DOS do HOT grafeno; ( c ) o BZ correspondente de HOT grafeno

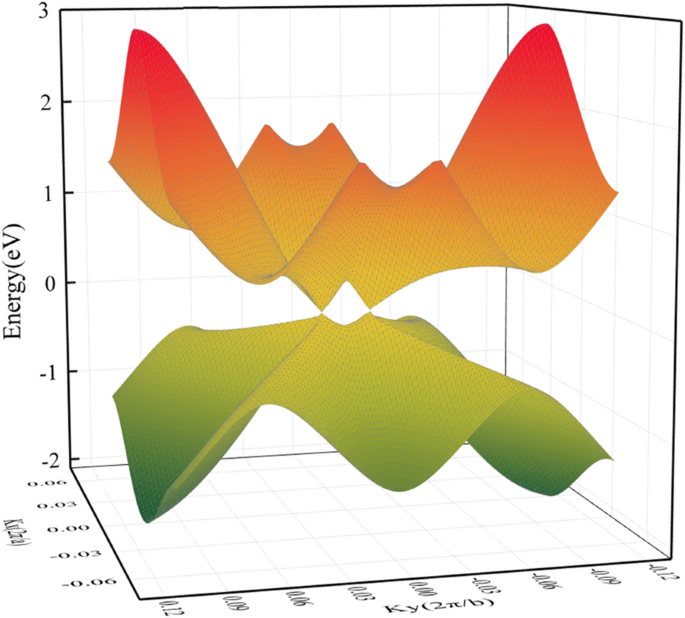
Estrutura da banda 3D do HOT grafeno

Estruturas geométricas e eletrônicas de HOT Nanotubos de grafeno

O QUENTE tubos de grafeno são enrolados do QUENTE folha de grafeno em várias direções simbolizadas por um índice no 2D HOT rede de grafeno (Fig. 3a). Este índice é denotado como ( l, m ) n baseando-se em dois vetores unitários a e b . Símbolo ( l, m ) [18, 20, 21] representa diferentes direções no HOT folha de grafeno, n representa o número de unidades de perímetro (Fig. 3b ec) usadas para enrolar os tubos. Sob a simetria de reversão do espaço do HOT célula unitária de grafeno, o símbolo do nanotubo está confinado a 0 ≤ l e 0 ≤ m para evitar uma correspondência muitos para um. O número de estruturas geométricas possíveis do HOT nanotubos de grafeno é infinito, uma vez que existem infinitas opções para diâmetros e direções de rolamento. Entre um número tão grande de nanotubos, apenas duas direções, (0,1, 1,0), são selecionadas em nosso estudo. Isso ocorre porque o arranjo helicoidal de átomos em outras direções é apenas periódico e possui um comprimento quase infinito de célula unitária ao longo do eixo do tubo. Uma célula unitária tão grande não é realista em nossos cálculos. Direções de rolamento diferentes entre (1,0) n e (0,1) n os tubos resultam nas diferenças na geometria e na situação de ligação. Dois tubos, (1,0) 6 e (0,1) 4, são representados na Fig. 3d e e para descrever as diferenças geométricas entre as duas direções de rolamento. O arranjo dos polígonos ao longo da direção (1,0) pode ser dividido em dois padrões:C ₄ –C ₆ –C ₈ (laranja) e C ₈ –C ₆ –C ₄ (azul) que são exatamente opostos um ao outro. Esses dois padrões opostos se alternam ao longo da direção circunferencial do tubo. Na direção (0,1), os polígonos dispostos ao longo do eixo do tubo também têm dois padrões:C ₄ –C ₈ (azul) e C ₆ –C ₆ (laranja). Dois C ₄ –C ₈ padrões alternam com um C ₆ –C ₆ padrão ao longo da direção circunferencial.

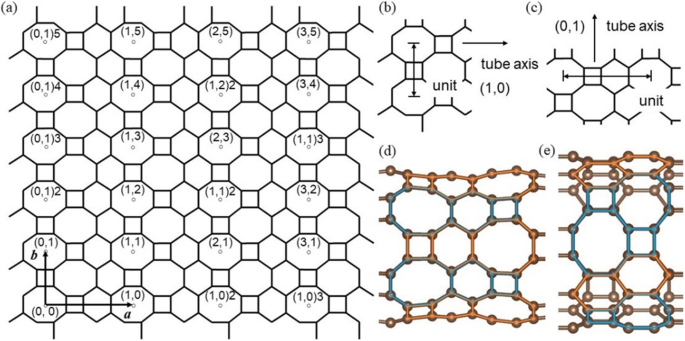
( a ) Diferentes tubos são indicados pelo símbolo ( l, m ) n , com ( l, m ) significa direção de rolamento com base no vetor unitário a e b e n para o número de unidades de diâmetro do tubo; ( b ) unidade de diâmetro na direção (1,0); ( c ) unidade de diâmetro na direção (0,1); ( d ) estrutura geométrica de um (1,0) 6 QUENTE nanotubo de grafeno; ( e ) estrutura geométrica de um (0,1) 4 QUENTE nanotubo de grafeno

Para revelar o custo de energia no enrolamento de uma folha em tubos, definimos a energia da curvatura (Fig. 4) E _cur Como:
$$ {E} _ {\ mathrm {cur}} ={E} _ {\ mathrm {tubo}} ^ {\ mathrm {at}} - {E} _ {\ mathrm {folha}} ^ {\ mathrm { at}} $$
onde \ ({E} _ {\ mathrm {tubo}} ^ {\ mathrm {at}} \) é a energia média dos átomos no nanotubo, e \ ({E} _ {\ mathrm {folha}} ^ {\ mathrm {at}} \) é a energia média dos átomos na folha 2D. O (1,0) n os tubos exibem um custo de energia menor do que os nanotubos de grafeno, enquanto os (0,1) n os tubos são quase iguais aos nanotubos de grafeno de poltrona, exceto por vários tubos ultrapequenos. Tais resultados também sugerem que é possível sintetizar o HOT nanotubos de grafeno em experimentos. Deve-se notar que o tubo (1,0) 1 é muito pequeno porque seu diâmetro é ainda mais curto que o comprimento de ligação do carbono.

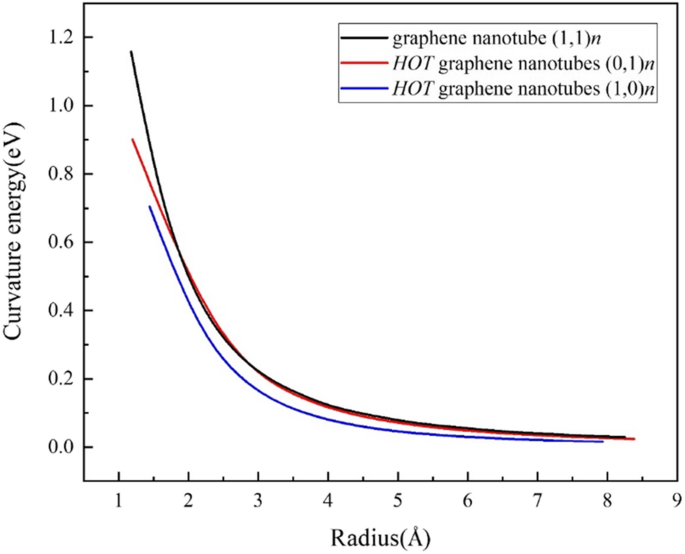
Energias de curvatura do QUENTE nanotubos de grafeno e nanotubos de grafeno

A estrutura de banda eletrônica calculada e DOS do nanotubo (0,1) 6 (Fig. 5b) indicam um caráter semimetálico. Quando o QUENTE a folha de grafeno é enrolada em um nanotubo, seu 2D BZ é reduzido para 1D BZ como resultado das novas condições de contorno periódicas nos nanotubos. As condições de contorno periódicas ao longo da direção circunferencial do tubo permitem apenas vetores de onda "em torno" da circunferência do nanotubo e esses vetores são quantizados [49]. As condições de contorno periódicas ao longo do eixo do nanotubo permanecem as mesmas da folha 2D, então os vetores de onda permanecem contínuos ao longo do eixo do nanotubo. De acordo com o esquema de dobramento de zona, a estrutura de banda eletrônica de um nanotubo específico é dada pela sobreposição das bandas de energia eletrônica da folha 2D correspondente ao longo do k especificamente permitido linhas [50]. Como os vetores de onda quantizados no meio do BZ do HOT o grafeno sempre cruza o ponto de Dirac (ponto F na Fig. 5a), um ponto de Dirac não degenerado (ponto F na Fig. 5b) e o cone de Dirac aparece nas estruturas de banda do (0,1) n HOT nanotubos de grafeno, resultando na semimetalicidade de todos os (0,1) n nanotubos. O tubo (0,1) 6 é calculado para avaliar a semimetalicidade deste conjunto de (0,1) n nanotubos na Fig. 5. Estrutura da banda do (0,1) 6 HOT os nanotubos de grafeno mostram um ponto de cruzamento de bandas de energia no nível de Fermi e o DOS correspondente não mostra nenhum estado no nível de Fermi que verifica a semimetalicidade do sistema. Como o cone de Dirac em (0,1) n tubos é originado do HOT folha de grafeno, a coordenada calculada do ponto de Dirac no nanotubo (0,1) 6 é a mesma que em HOT folha de grafeno que é (0, 0,0585, 0). A velocidade de fermi calculada no ponto de Dirac em (0,1) 6 nanotubo é 6,76 × 10 ⁵ m / s, perto de 6,27 × 10 ⁵ m / s no QUENTE folha de grafeno.

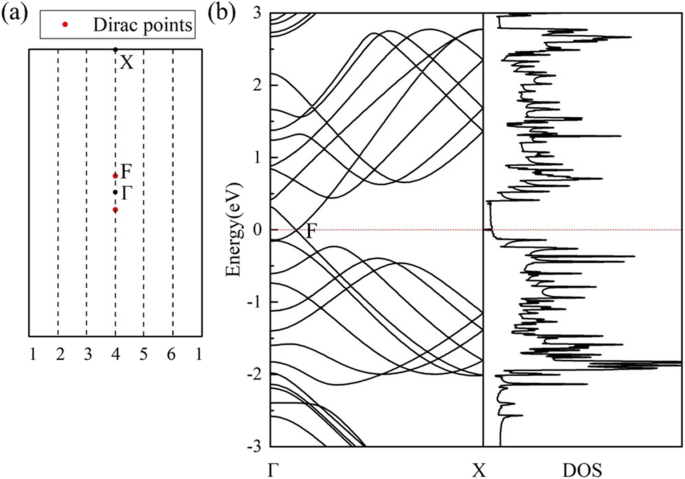
( a ) O primeiro BZ do HOT grafeno com permitido k linhas (linhas tracejadas) para o (0,1) 6 nanotubo. F é o ponto de Dirac. ( b ) As estruturas de banda calculadas e DOS de (0,1) 6 nanotubos

A evolução da estrutura da banda de (0,1) n nanotubos com raios de tubo diferentes (Fig. 6a) revelam que o QUENTE nanotubos de grafeno (0,1) n são semimetálicos ( n ≥ 3) e transformar em metal ( n =2) e depois voltar para semimetal ( n =1). Essa mudança sob um raio pequeno resultou do chamado efeito de curvatura [26]. Na situação de nanotubos ultrapequenos (por exemplo, (0,1) 2 e (0,1) 1), a curvatura tem um efeito não desprezível no esquema de dobramento de zona. O comprimento da ligação e o ângulo da ligação sofrem uma alteração não desprezível dentro da grande curvatura, que tem influência na estrutura da banda eletrônica. As estruturas de banda de tais nanotubos não são mais uma simples superposição de bandas de energia nos vetores de onda permitidos. Esta mudança de ligações modifica as condições que definem o k ponto em que bandas ocupadas e não ocupadas se cruzam (em um ponto que rotulamos k _F ) e deslocar o k _F longe dos pontos de Dirac originais, que é chamado de k _F efeito de deslocamento [24, 25]. Como resultado, no (0,1) n HOT nanotubos de grafeno, o k _F se afasta de sua posição original ( k _QUENTE ) no QUENTE folha de grafeno (ponto F na Fig. 5a). E a mudança de direção de k _F é calculado para estar ao longo do vetor de onda permitido (linhas tracejadas na Fig. 5a), resultando em nenhuma alteração da semimetalicidade (Fig. 6a ( n ≥ 3)). De acordo com a coordenação calculada de pontos Dirac, o k _F o efeito de deslocamento torna-se não desprezível em (0,1) 5 com um raio de tubo de 5,988 Å, cujo ponto de Dirac ( k _F ) muda para (0,0.0626,0) do ponto original ( k _QUENTE ) em (0,0.0594,0) em QUENTE folha de grafeno. Conforme o raio do tubo fica menor, o k _F continua mudando e atinge o ponto (0,0.0712,0) no tubo (0,1) 3. No tubo (0,1) 2, o k _F muda para (0,0.0835,0) onde o ponto de Dirac desce abaixo do nível de Fermi, resultando em um sistema metálico. O desaparecimento da semimetalicidade em (0,1) 2 indica um desvio do k _F efeito de deslocamento no (0,1) n nanotubos ( n ≥ 3). Além disso, o tubo (0,1) 1 torna-se semimetálico novamente em sua estrutura de banda e o DOS (Fig. 6b). Nossa análise de estado do elétron do (0,1) n HOT nanotubos mostra estados π sobrepostos em n ≥ 2, que geralmente é considerado a origem da semimetalicidade dos nanotubos de grafeno [18, 24]. No entanto, a análise de estado do elétron correspondente do HOT nanotubo de grafeno (0,1) 1 mostra uma hibridização σ-π em que uma banda σ * baixa intersecta o nível de Fermi e se junta ao cone de Dirac (linhas azuis na Fig. 6a). A coordenação do ponto de Dirac, que é (0,0.18345,0), também exibe uma distinção de outro (0,1) n HOT nanotubos de grafeno. A velocidade de Fermi calculada é 4,47 × 10 ⁵ m / s, inferior a 6,27 × 10 ⁵ m / s em QUENTE folha de grafeno e valores para outro (0,1) n nanotubos (~ 6,76 × 10 ⁵ em). Uma forma obviamente diferente de sua estrutura de banda também é mostrada na Fig. 6a. Todos esses caracteres verificam que a semimetalicidade do HOT O nanotubo de grafeno (0,1) 1 é originado da hibridização σ-π. Em resumo, com a curvatura crescente, o k _F efeito de deslocamento surge em n =5, torna-se mais eficaz em 4 ≥ n ≥ 2, e é finalmente substituído pelo efeito de hibridização σ-π em n =1.

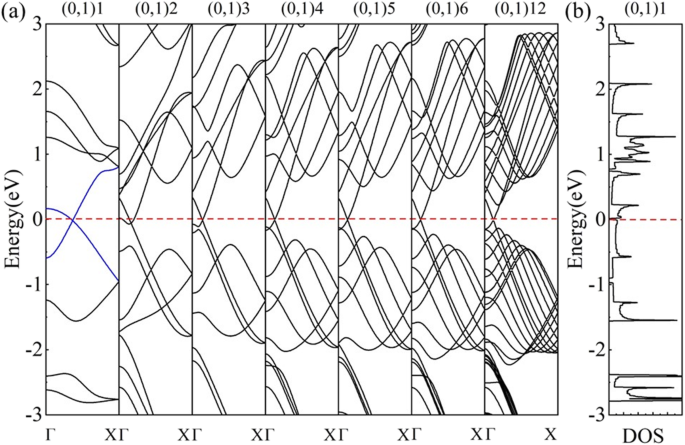
( a ) Evolução da banda de (0,1) n nanotubos ( n =1, 2, 3, 4, 5, 6, 12); ( b ) DOS do (0,1) 1 nanotubo

Em outra direção de rolamento, a estrutura de banda calculada de (1,0) 6 (Fig. 7b) mostra a semicondutividade. Os 6 vetores de onda (linhas tracejadas) são paralelos a Γ-M, cruzando o ponto Г no meio do BZ de HOT grafeno (Fig. 7a), e abra um gap de 0,46 eV conforme mostrado no DOS (Fig. 7b). Nessa direção de rolamento, os vetores de onda permitidos no meio do BZ nunca incluem os pontos de Dirac, o que resulta em intervalos de banda diferentes de zero neste conjunto de nanotubos. A evolução da banda revela uma mudança de lacunas de banda com raios diferentes na Fig. 8a. O (1,0) n QUENTE nanotubos de grafeno são semicondutores ( n ≥ 4). A banda de valência máxima (VBM) e a banda de condução mínima (CBM) se aproximam do tubo (1,0) 6 para o tubo (1,0) 4 e então se cruzam no tubo (1,0) 3 com um raio de 2,17 Å. Este ponto de cruzamento está exatamente no nível de Fermi localizado em (0,0791,0,0). O DOS calculado (Fig. 8b) apresenta 0 estados ao nível de Fermi de (1,0) 3, verificando a semimetalicidade. Quando o raio do tubo diminui para (1,0) 2, uma lacuna de 0,848 eV se abre novamente. O CBM e o VBM de (1,0) 2 estão localizados no ponto Γ e no ponto M, respectivamente, indicando um gap indireto. Esta mudança no VBM implica uma origem diferente para a semicondutividade em (1,0) 2. Um estudo mais aprofundado da mudança de intervalo de banda no (1,0) n HOT nanotubos de grafeno são mostrados na Fig. 9. A evolução do intervalo de banda como uma função de n (3 ≤ n ≤ 23) indica que a folga da banda é ajustável com os tamanhos dos tubos. Além disso, em vez de ser monótono, a dependência do gap com o tamanho do tubo tem uma forma de zigue-zague (Fig. 9 curva preta). O mínimo global em (1,0) 15 apresenta um gap zero. A semimetalicidade de (1,0) 15 é posteriormente confirmada pela estrutura da banda e DOS (Fig. 9g). A partir do esquema de dobramento de zona, sabemos que a estrutura de banda dos nanotubos é a superposição da estrutura de banda da folha 2D ao longo do k correspondente quantizado linhas [50]. Assim, a semimetalicidade indica que pelo menos um dos k permitidos linhas (linhas tracejadas na Fig. 7a) cruzam os pontos de Dirac (pontos vermelhos na Fig. 7a) em n =15. Caso contrário, se o permitido k as linhas têm uma distância dos pontos Dirac ( k _QUENTE ), uma lacuna de banda aparecerá no nanotubo. Além disso, esta distância entre k _F e o k as linhas são proporcionais aos intervalos de banda, pois a dispersão da banda perto do cone de Dirac é linear [25]. O Δk _m mede a distância mais curta entre k _F e k _m linhas de número quântico m . Calculamos esta distância Δk _m entre os pontos Dirac ( k _QUENTE ) e o permitido k linhas no QUENTE grafeno e plote-o (linha vermelha) junto com as lacunas de banda (linha preta) na Fig. 9. Em primeiro lugar, todos os k permitidos linhas têm um número quântico m . Quando n ≤ 7 (por exemplo, Fig. 9a), a distância mais curta ( Δk _m ) está entre k _QUENTE e o primeiro k linha, k ₁ , que fica no ponto Γ constantemente (insira o gráfico (a) na Fig. 9). Nesta situação, Δk _m é constante como k ₁ e k _QUENTE são constantes e independentes do tamanho do tubo. No entanto, como permitido k as linhas se tornam mais densas em nanotubos maiores (7 ≤ n ≤ 17), o k ₂ torna-se o mais próximo de k _QUENTE (por exemplo, Fig. 9b). Nesta situação, o k ₂ aproxima-se do ponto Dirac do BZ externo com raios crescentes do tubo; portanto, mostra um declínio de Δk _m na Fig. 9 (7 ≤ n ≤ 17). n =17 é um ponto de viragem onde k ₂ quase intersecta o ponto Dirac, resultando em um mínimo local da distância Δk _m (Fig. 9c). Conforme o raio continua aumentando, o k ₂ atravesse o k _QUENTE ponto e continua a se afastar dele para o ponto Г resultando em um aumento da distância novamente em 17 ≤ n ≤ 24 (por exemplo, Fig. 9d). Ao mesmo tempo, k ₃ está se aproximando do ponto Dirac. k ₃ chega mais perto de k _QUENTE do que k ₂ e começa uma nova diminuição na distância Δk _m em n ≥ 24. Como as lacunas de banda são proporcionais a esta distância Δk _m [25], a curva de gap mostra a mesma forma que o Δk _m enredo ( n ≥ 7). E é revelado que as lacunas de banda mudam nos ciclos:o k _m se aproxima do ponto Dirac ( k _QUENTE ) causando um declínio do intervalo de banda, então atravessa o ponto de Dirac resultando em um mínimo local, então se afasta do ponto de Dirac causando um aumento do intervalo de banda e é finalmente substituído pela próxima linha k _{m + 1} entrar no próximo ciclo. Em resumo, a razão pela qual as lacunas de banda estão mudando com o tamanho do tubo ( n ≥ 7) é que o k as linhas estão se movendo com diferentes tamanhos de tubos, portanto, alteram a distância Δk _m entre k _QUENTE e o permitido k linhas que são proporcionais aos intervalos de banda.

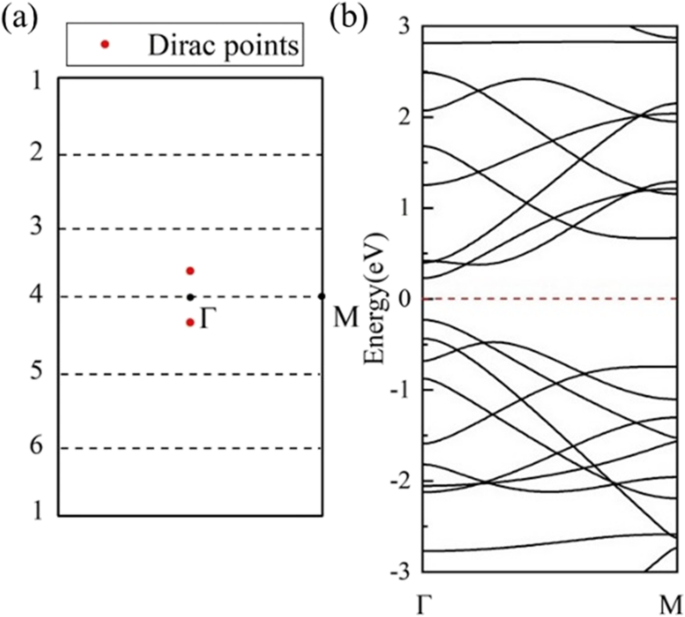
( a ) O primeiro BZ do HOT grafeno com permitido k linhas (linhas tracejadas) para o (1,0) 6 nanotubos; ( b ) estruturas de banda do (1,0) 6 nanotubo

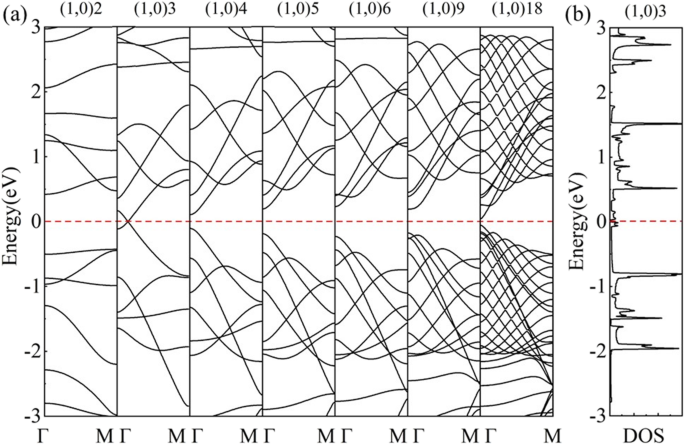
( a ) Evolução da banda de HOT nanotubos de grafeno (1,0) n ( n = 2, 3, 4, 5, 6, 9, 18); ( b ) DOS do (1,0) 3 nanotubo

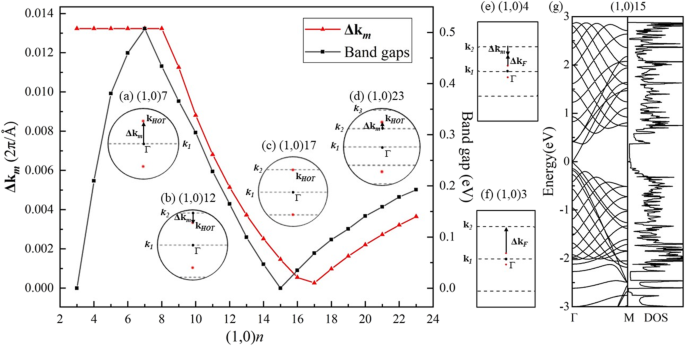
Gaps de banda calculados (linha preta) e distância Δk _m (linha vermelha) entre k _QUENTE e o mais próximo k linha em (1,0) n tubos. Os gráficos inseridos são o BZ próximo ao ponto Γ com k permitidos linhas k _m ( m =1, 2, 3) (linhas tracejadas) e o ponto Fermi de QUENTE nanotubos de grafeno k _QUENTE (pontos vermelhos) no tubo ( a ) (1,0) 7, ( b ) (1,0) 12, ( c ) (1,0) 17, ( d ) (1,0) 23, ( e ) (1,0) 4, e ( f ) (1,0) 3. ( g ) Estruturas de banda e DOS do tubo (1,0) 15

Embora o Δk _m curva e a curva de gap de banda têm semelhanças na forma, as diferenças entre elas também são óbvias, que é que o Δk _m o gráfico mostra um “atraso” na mudança em n ≥ 7 e torna-se completamente diferente do gráfico de lacuna de banda em 3 ≤ n ≤ 7. A razão é que o ponto de Fermi em QUENTE nanotubos de grafeno ( k _F ) é assumido como tendo a mesma coordenada que o ponto Fermi original em HOT grafeno ( k _QUENTE ) na seção anterior, onde a mudança do gap foi explicada. No entanto, o ponto de Fermi ( k _F ) nos nanotubos se afasta do ponto de Fermi de origem ( k _QUENTE ) em QUENTE folha de grafeno sob o efeito de curvatura. Portanto, o k _F deslocamento (Δ k _F = k _F - k _QUENTE ) efeito contribui para as incompatibilidades entre a distância Δk _m e as lacunas de banda. Conforme calculado em (0,1) n tubos (Fig. 6), o k _F em (1,0) n os tubos também se deslocam para o BZ externo em direção ao ponto simétrico X sob a curvatura. Portanto, quando o mais próximo k _m senta-se entre o k _QUENTE e o ponto Γ, a distância Δk _m subestima o gap (por exemplo, 17 ≤ n ≤ 24 na Fig. 9d). Caso contrário, o mais próximo k _m sentado no exterior do k _QUENTE ponto, resulta em uma superestimativa do gap (por exemplo, 7 ≤ n ≤ 17 na Fig. 9b). Em pequenos nanotubos (3 ≤ n ≤ 7), o k _F efeito de deslocamento é aumentado sob a grande taxa de crescimento da curvatura; conseqüentemente, causa um drástico k _F deslocando e muda o gap. Quando o raio está ficando menor do que n =8, o k ₁ torna-se o mais próximo do k _QUENTE indicando uma constante Δk _m . No entanto, o k _F efeito de deslocamento é tão forte para mover o k _F mais longe de k ₁ mas mais perto do k ₂ (Fig. 9e). O k _F efeito de deslocamento vence a competição com o k linhas se movendo e começa a determinar as lacunas de banda desde então ( n ≤ 7). O k _F continua mudando para o k ₂ em alta velocidade de modo que a distância entre k _F e k ₂ fica cada vez menor. Portanto, de (1,0) 7 para (1,0) 3, o gap diminui (Fig. 9). Enfim, o k _F alcança k ₂ e cruza em n =3 (Fig. 9f). Este cruzamento de um k alinhe com o k _F resulta no ponto de Dirac no tubo (1,0) 3 que dá origem à semimetalicidade (Fig. 8), conforme discutido nas seções anteriores. Diminuição adicional do raio para n =2 abre uma lacuna de 0,848 eV no tubo (1,0) 2 (Fig. 8). Esta lacuna é tão grande e é considerada fora do alcance k _F esquema de deslocamento e, portanto, não é plotado na Fig. 9. Em resumo, há um mecanismo de competição entre o k linha em movimento e o k _F mudando na determinação das lacunas de banda. O k _F deslocamento de condutores de efeito em tubos pequenos (7 ≥ n ≥ 3), enquanto o k linha de movimentação em tubos grandes ( n ≥ 8) onde o k _F o efeito de deslocamento está desbotado. A quantidade de k _F o deslocamento é estimado em 0,0015 2π / Å em n =15 e 0,0238 2π / Å em n =3 porque os intervalos de banda são 0 eV onde o k deslocado _F o ponto está no permitido k linhas. Pode-se ver que o k _F o deslocamento é 15,86 vezes maior em um tubo pequeno (tubo (1,0) 3) do que em um tubo grande (tubo (1,0) 15).

Em QUENTE grafeno, os átomos de carbono são todos coordenados em três partes, portanto, o quarto elétron de valência desempenha um papel fundamental em sua condutividade. A banda calculada decomposta densidade de carga ± 0,15 eV em torno do nível de Fermi (Fig. 10) mostra a distribuição dos elétrons no cone de Dirac. Only the electrons on the 8–8 bonds (Fig. 10a) have an overlapping and the side view (Fig. 10b) shows that the electrons distribute perpendicularly to the HOT graphene sheet, which indicates that the Dirac cone consists of π states. Therefore, the electron overlapping on the 8–8 bonds (enlarged side view in Fig. 10a) is considered to be localized π states. In big nanotubes such as (0,1)6 (Fig. 10c), the charge density is similar to the HOT graphene sheet showing localized π bonds on 8–8 bonds (enlarged side view in Fig. 10c). As the radius decreases to (0,1)2, whose conductivity transforms to metal (Fig. 6), the 8–8 bonds show several deformations (Fig. 10d). Firstly, these states are no longer symmetric with respect to the tube wall. The overlapping of the π state outside the tube wall breaks apart while the π states inside keep overlapping with each other. Besides the 8–8 π bonds, new π bonds form on 4–8 in (0,1)2. These bonds are similar to the deformed 8–8 bonds:separated π states outside the tube wall and overlapping π states inside the tube wall. Every 4–8 bond connects two 8–8 bonds adjacent to it, forming a delocalized π overlapping inside the tube along the tube axis direction. The enlarged side view in Fig. 10d shows the connection between 4 and 8 and 8–8 bonds as a segment of the whole delocalized bond. Therefore, the metallicity in tube (0,1)2 can be attributed to the delocalized π overlapping in the 4–8 and 8–8 bonds along the tube axis direction which provides a pathway for the electrons to travel along the tube. When the radius keeps decreasing, the conductivity disappears and the (0,1)1 tube becomes a semimetal again (Fig. 6). Different from all the other (0,1) n tubes, the 8–8 overlapping (Fig. 10e) in nanotube (0,1)1 is totally broken up; instead, 4–8 overlapping and 4–6 overlapping plays the major role in the Dirac cones. These two bonds belong to two opposite edges in the same carbon tetragons and are arranged parallel to the tube axis. Furthermore, they are no longer π states. Based on the electronic state analysis, a σ-π hybridization takes place at the Fermi level under such a strong curvature in nanotube (0,1)1. It is verified by the charge density which shows the electron states distribute closely to the bond axis (enlarged side view in Fig. 10e). Strongly modified low-lying σ states are introduced at the Fermi level as discussed in the preceding sections (blue line in Fig. 6). Therefore, the σ-π hybrid states in the 4–8 and 4–6 bonds are considered the reason for the semimetallicity in (0,1)1, which is essentially different from the other semimetallic tubes (0,1) n ( n ≥ 3). In another set of HOT graphene nanotubes, the band gaps show adjustability with different tube radius (Fig. 9). The charge densities also present an evolution with the tube radii in Fig. 11. The band decomposed charge density of tube (1,0)9 in Fig. 11a and b shows the localized π states overlapping in both the VBM and CBM. The VBM is contributed by π states on 6–6 bonds and 8–8 bonds (Fig. 11a). The CBM is contributed by π states on part of 4–8 and 6–8 bonds (Fig. 11b). The 4–6 bonds have no states on both of the VBM and CBM. When the (1,0) n tubes become semimetallic at some specific radii, such as n = 15, the VBM and CBM meet with each other. Band decomposed charge density ± 0.15 eV around the Fermi level of (1,0)15 nanotube show the different distribution of electrons from the semiconductive tubes. More importantly, it exhibits a similar distribution to the semimetallic HOT graphene sheet and (0,1) n tubos. The localized π bond of (1,0)15 only locates on the 8–8 bonds. This redistribution of electron in (1,0) n tubes causes the conductivity change.

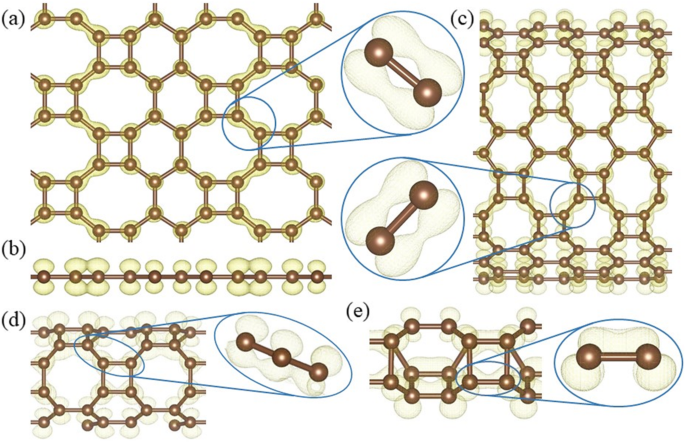
Band decomposed charge densities around the Fermi level of (a ) HOT graphene, (b ) the corresponding side view, and HOT graphene nanotubes (c ) (0,1)6, (d ) (0,1)2, and (e ) (0,1)1 with corresponding enlarged side views

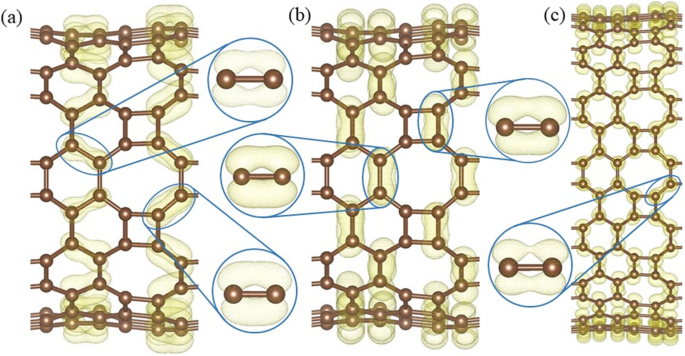
Band decomposed charge densities at (a ) VBM, and (b ) CBM of HOT graphene nanotube (1,0)9; ( c ) charge densities around the Fermi level of the HOT graphene nanotube (1,0)15 with the localized π bond in the enlarged side view

Conclusão

A new graphene allotrope named HOT graphene is constructed by carbon hexagons, octagons, and tetragons showing Dirac cone and high Fermi velocity, which implies that the honeycomb structure is not an indispensable condition for Dirac fermions to exist. The semiconductivity of HOT graphene is dependent on the localized π bonding. A corresponding series of nanotubes is rolled up from the HOT graphene sheet and shows distinctive electronic structures depending on the topology. The set of (0,1) n ( n ≥ 3) HOT graphene nanotubes reveals a character of semimetallicity and Dirac cones that are composed by π states. A non-negligible k _F shifting along the allowed k line arises under the curvature effect when the tube radius gets smaller (3 ≤ n ≤ 5). However, the ultra-small nanotube (0,1)2 begins to deviate from the π state-based k _F shifting effect showing a transformation to metallicity. Finally, an σ-π hybridization takes the place of the π states at Fermi level in nanotube (0,1)1, where a low-lying σ* band intersection appears at the Fermi level and forms a semimetallicity again. Another set of tubes (1,0) n shows various band gaps (0~ 0.51 eV), which is continuously adjustable with the tube size. The band gaps of (1,0) n ( n ≥ 3) nanotubes turn out to be determined by a competition mechanism between the k line moving and the k F shifting effect. The zone-folding approximation indicates a k line moving and results in the zigzag and periodical band gap changing curve in big tubes (n ≥ 8), while the k F shifting effect gets stronger and causes a dramatic decrease of band gaps in small tubes (7 ≥ n ≥ 3). Zero-gap semimetallic tubes appear periodically under the competition.

Disponibilidade de dados e materiais

Authors declare that the datasets used and/or analyzed during the current study are available to the readers and included in this article.

Abreviações

1D:: One-dimensional
2D:: Bidimensional
3D:: Tridimensional
BZ:: Zona de Brillouin
CBM:: Banda de condução mínima
DFT:: Teoria da densidade funcional
DOS:: Densidade de estados
GGA:: Generalized-Gradient Approximation
HOT :: Hexagons, octagons, and tetragons
PBE:: Perdew–Burke–Ernzerh
VASP:: Pacote de simulação Ab initio de Viena
VBM:: Banda de valência máxima

Nanocomplexos de óxido de grafeno modificado com folato funcionalizado / PEI siRNA para terapia gênica direcionada do câncer de ovário A preparação econômica de pontos de carbono fluorescente verde para bioimagem e administração intracelular aprimorada de medicamentos

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias