Observação de oscilações do tipo Aharonov-Bohm dependentes do nível de Landau em um isolador topológico

Resumo

Nós estudamos as oscilações quânticas no BiSbTe ₃ isolante topológico. Além da oscilação de Shubnikov-de Haas (SdH), as oscilações do tipo Aharonov-Bohm (ABL) também são observadas. O período de oscilação ABL é constante em cada nível de Landau (LL) que é determinado a partir da oscilação SdH. Os períodos de oscilação ABL mais curtos são observados em LLs mais baixos. O período de oscilação é proporcional à raiz quadrada do LL nas temperaturas. A proporção do período de oscilação ABL para a massa efetiva é uma dependência LL fraca. A oscilação ABL dependente de LL pode originar-se da massa efetiva dependente de LL.

Introdução

A interferência de Aharonov-Bohm (AB) se origina da interferência da função de onda da portadora em um loop que pode ser anel padronizado [1, 2], estrutura geométrica do material [3-6, 8-11] ou trajetória de transporte da portadora [12]. O campo magnético, B , através do loop irá induzir mudança de fase da função de onda portadora que leva a oscilações periódicas de interferência da função de onda. Este período de oscilação é sensível às características de transporte da portadora, como comprimento de coerência da portadora e mobilidade [3, 12]. A interferência quântica é uma excelente ferramenta para detectar características de transporte de materiais e entender mecanismos intrínsecos. Devido ao curto comprimento de coerência da portadora e ao pequeno quantum de fluxo, a interferência quântica é relatada principalmente em nanofios de alta mobilidade ou nanoanéis padronizados em B baixo [3-6, 8-11]. Relatórios em um sistema macroscópico em alto B são raros. Os trabalhos sobre interferência quântica AB em alto B são menos investigados e o mecanismo relacionado é menos compreendido.

Neste trabalho, as oscilações quânticas foram realizadas em um BiSbTe ₃ macroflake isolante topológico em alto B . Além da oscilação Shubnikov-de Haas (SdH), a oscilação semelhante a Aharonov-Bohm (ABL) foi observada. O período de oscilação ABL é B -dependente e é diferente da oscilação AB tradicional, cujo período de oscilação é independente de B . O período de oscilação ABL observado é constante em cada nível de Landau (LL), que é determinado a partir da oscilação SdH. Os períodos de oscilação mais curtos são observados em LLs mais baixos. O período de oscilação é proporcional à raiz quadrada do LL nas temperaturas. A proporção do período de oscilação ABL para a massa efetiva é uma dependência LL fraca. A oscilação ABL dependente de LL pode originar-se da massa efetiva dependente de LL.

Método Experimental

A condição de crescimento do BiSbTe ₃ cristal único é o mesmo que nosso trabalho anterior sobre os isoladores topológicos [13-16]. Nosso trabalho anterior demonstrou que TI com uniformidade extremamente alta pode ser obtido usando o método RHFZ [13–16]. Espectro Raman, EDS e XPS provou que o cristal é BiSbTe ₃ . O BiSbTe ₃ flocos de cristal único foram obtidos pelo método da fita adesiva. A geometria do floco clivado tem aproximadamente 3 mm de comprimento, 2 mm de largura e 170 μ m de espessura. As medições de magnetotransporte foram realizadas usando a técnica padrão de seis sondas em um aparelho comercial (Quantum Design PPMS) com um B de até 14 T. O B foi aplicado perpendicularmente à grande superfície clivada. Os pontos de dados são obtidos por 100 Gauss na região do campo magnético entre 6 e 14 T no modo de campo magnético constante, em vez do modo de campo magnético de varredura.

Resultados e discussão

A Figura 1 mostra as magnetorresistências (MRs) em função de B . O R (14T) / R (0T) atinge 10 e é maior do que a maioria dos valores relatados em Bi _x Sb _{2− x} Te _y Se _{3− y} isoladores topológicos [17-23, 23-33]. As investigações teóricas e experimentais apóiam que a razão MR é proporcional à mobilidade do portador [34]. A alta razão MR medida apóia a alta qualidade de nosso BiSbTe ₃ amostra. A inserção superior esquerda revela o d R / d B como uma função de 1 / B . Ele revela que oscilações periódicas e picos e quedas de oscilação são iguais B a 2 e 8 K. Isso é conhecido como oscilação SdH que se origina de um sistema bidimensional. O período de oscilação SdH corresponde ao vetor momentum de Fermi, k _f . A inserção inferior direita mostra a transformada rápida de Fourier (FFT) da oscilação SdH. Um pico agudo em 48 T é observado para 2 e 8 K. Seguindo a relação de Onsager, pode-se estimar k _f a \ (F =\ frac {\ hbar k_ {f} ^ {2}} {2e} \), onde F é a frequência de oscilação SdH. O F =48 T leva ao k _f =3.8Å ⁻¹ , que é consistente com o valor observado de ARPES de um lote diferente do mesmo cristal e de valores relatados na literatura [35]. Isso suporta a alta qualidade e uniformidade de nosso BiSbTe ₃ cristal. Assim como a oscilação SdH, a inserção superior esquerda revela oscilações com um curto período. Para suprimir a influência da oscilação SdH e extrair as características de oscilação, o d ² R / d B ² é realizado.

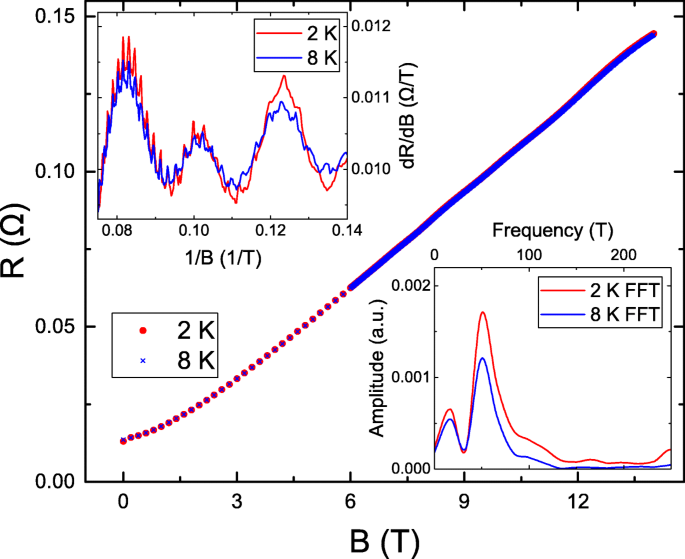
A magnetorresistência em função dos campos magnéticos a 2 e 8 K. A inserção superior esquerda mostra o d R / d B em função de campos magnéticos inversos. Ele revela oscilações periódicas. A inserção inferior direita mostra a transformada rápida de Fourier da oscilação SdH e um pico agudo em 48 T para 2 e 8 K

A Figura 2 exibe o d R / d B e d ² R / d B ² como uma função de B a 2 e 8 K. As linhas de pontos marcam os picos de oscilação em d ² R / d B ² , e as linhas tracejadas correspondem a B de LLs que são determinados a partir da frequência de oscilação SdH extraída. As oscilações periódicas são semelhantes à oscilação AB. O período de oscilação AB é expresso como \ (\ Delta B =\ frac {\ Phi} {A} \). Φ é o quantum de fluxo, onde \ (\ frac {h} {e} \), e A é a área da geometria em loop pelas trajetórias da portadora de contagem de relógio e anti-relógio em uma estrutura confinada. Devido ao pequeno quantum de fluxo, a oscilação AB é observada principalmente em confinamento por nanoestruturas artificiais [1, 2], como nano-anéis e nanofios [3-11]. Recentemente, é relatado que a trajetória de espalhamento elástico da portadora pode formar uma série de loops fechados conectados em um sistema macroscópico. A B o fluxo através desses loops induziria a mudança de fase da função de onda portadora e levaria a oscilações ABL periódicas [12]. O comprimento de espalhamento elástico extraído é de aproximadamente 150 nm, que corresponde ao período de oscilação com 0,02 T e é consistente com nossa observação experimental.

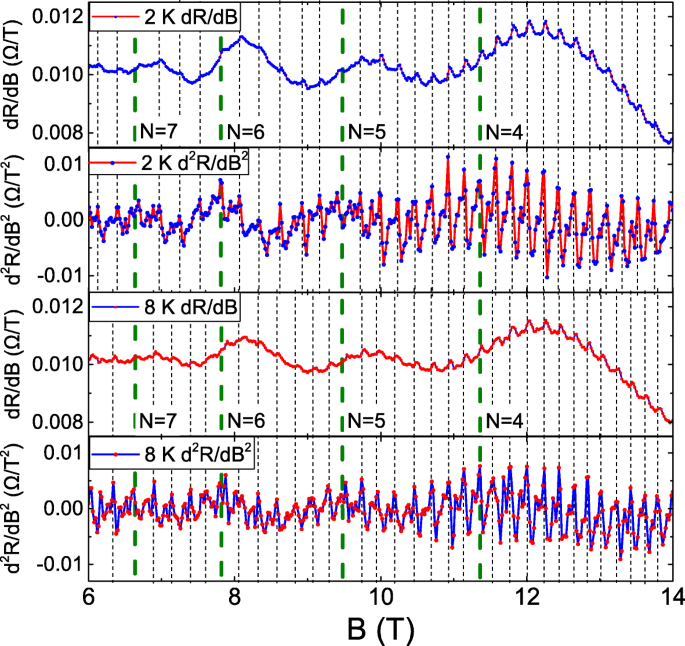
O d R / d B e d ² R / d B ² como uma função de B a 2 e 8 K. Mostra oscilações periódicas e o período de oscilação é a dependência do nível de Landau

Seguindo as linhas pontilhadas na Fig. 2, pode-se notar que o período de oscilação é constante em cada LL e o período de oscilação é menor em LLs mais baixos. Este comportamento é diferente da oscilação AB tradicional. Para extrair e determinar esses períodos de oscilação, FFT é executado em diferentes LLs. A Figura 3 mostra o FFT em diferentes LLs em 2 e 8 K, e revela claramente a maior frequência de oscilação em LLs mais baixos em 2 e 8 K.

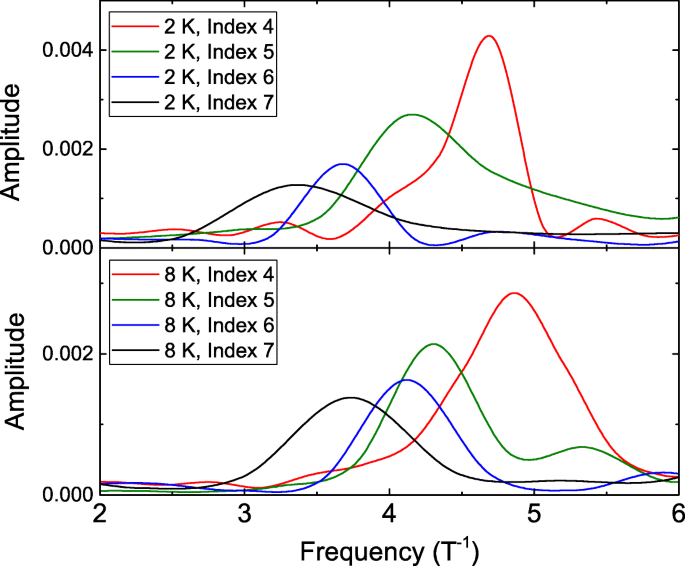
A transformação rápida de Fourier do d R / d B em diferentes níveis e temperaturas de Landau. O pico de frequência de oscilação mais alto é observado em níveis mais baixos de Landau

Uma oscilação ABL dependente de LL semelhante é relatada no regime Hall quântico inteiro em gás de elétron bidimensional semicondutor [36, 37]. Ela foi interpretada como interferência construtiva de elétrons unidimensionais viajando ao longo de canais de borda ou como interferência de onda quântica de elétrons de borda. O caminho de transporte da portadora em diferentes canais de borda leva a diferentes áreas efetivas em um padrão confinado e, eventualmente, a diferentes períodos de oscilação ABL em canais de borda em diferentes LLs [38-40]. Outros estudos em interferômetros elétricos de Fabry-Perot em regime Hall quântico inteiro e fracionário revelam que o período de oscilação ABL está relacionado ao período de fluxo por \ (\ frac {\ Phi} {f} \), onde f é o LL totalmente ocupado nas constrições. Espera-se que o período de oscilação seja \ (\ frac {\ Phi} {A f} \), onde A é a área de geometria da forma confinada [41, 42].

A Tabela 1 lista os períodos de oscilação extraídos do FFT em diferentes LLs e temperaturas. A análise revela que a razão entre o período de oscilação e a raiz quadrada de LL é constante em cada temperatura. Isso é diferente do comportamento do interferômetro de Fabry-Perot, no qual a oscilação é inversamente proporcional aos LLs [41, 42]. Por outro lado, a interferência elétrica Fabry-Perot origina-se do acoplamento da trajetória da portadora entre diferentes LLs de dentro e fora de um padrão confinado [37]. A oscilação está fortemente relacionada à geometria padronizada. Não há padrões artificiais na superfície de nossas amostras e não deve haver canais de acoplamento adequados entre diferentes LLs. Além disso, os tamanhos de geometria de nossas amostras estão na escala milimétrica e o período de oscilação AB relacionado seria muito pequeno para ser detectado. Apesar dessas diferenças em relação aos trabalhos existentes, pensamos que, além da área geométrica e do comprimento de coerência da portadora, a característica intrínseca da portadora pode desempenhar um papel crítico na oscilação ABL dependente de LL [3, 43].

Seguindo a teoria de Lifshitz-Kosevich (LK), pode-se extrair parâmetros característicos dos portadores de transporte no estado de superfície do isolador topológico, e a dependência da temperatura da amplitude da oscilação SdH é expressa como
$$ \ Delta R_ {xx} (T, B) \ propto \ frac {\ lambda (T / B)} {\ text {sinh} (\ lambda (T / B))}, $$
onde \ (\ lambda (T / B) =(2 \ pi ^ {2} k_ {B} Tm_ {cyc}) / (\ hbar eB) \). A Figura 4 mostra a amplitude de oscilação SdH normalizada extraída em função da temperatura em diferentes LLs. Ela concorda bem com a teoria LK e revela tendências diferentes em diferentes LLs. Os resultados de ajuste apóiam que o m _cyc =0,152 m ₀ , 0,170 m ₀ , 0,185 m ₀ e 0,191 m ₀ , onde m ₀ é a massa do elétron livre, para N =4, 5, 6 e 7, respectivamente. Esses valores são consistentes com as massas efetivas relatadas em isoladores topológicos [21, 22]. Esta massa efetiva dependente do nível de Landau foi observada recentemente no semimetal 3D Dirac ZrTe ₅ [44]. No entanto, a origem da massa efetiva dependente do campo magnético ainda não está clara. É necessário um estudo mais aprofundado para esclarecer o mecanismo intrínseco. A massa efetiva diferente desviaria diretamente a característica intrínseca de transporte da portadora na superfície de Fermi, como a velocidade de Fermi, que está diretamente relacionada ao comprimento de coerência da fase da portadora. A massa efetiva mais alta levaria a um comprimento de coerência menor que corresponde ao período de oscilação do tipo AB mais longo. Isso é qualitativamente consistente com nossa observação experimental. Conforme mostrado na Tabela 1, a razão do período de oscilação do tipo AB para a massa efetiva mostra uma dependência LL fraca. A massa efetiva dependente do nível de Landau pode ser um dos efeitos intrínsecos que leva ao período de oscilação dependente de LL.

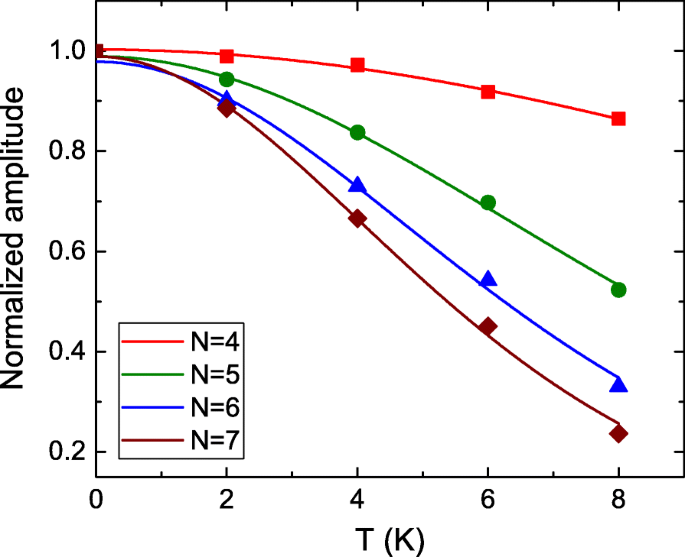
A amplitude de oscilação SdH normalizada extraída em função da temperatura em diferentes níveis de Landau. Ela concorda bem com a teoria LK e revela tendências diferentes em diferentes níveis de Landau

LL é uma característica de transporte de um sistema bidimensional. Isso indica que a oscilação dependente de LL pode ter se originado da portadora de estado de superfície em TIs. A fase de baga é uma característica dos transportadores. Extrair a fase de Berry pode ajudar a identificar a fonte dessas oscilações AB periódicas dependentes de LL. Definimos o número do índice de oscilação AB dividindo o B correspondente de picos de oscilação em d B / d B pelo período de oscilação relacionado no LL. Revela que o número índice de picos de oscilação em d B / d B corresponde a N +0,25, onde N é inteiro, para todas as oscilações em diferentes LLs e temperaturas. Isso também apóia que o período de oscilação AB está relacionado aos LLs. A Figura 5 mostra que os números do índice de oscilação AB são proporcionais a B em diferentes LLs e temperaturas. A interceptação é de 0,25, o que indica uma mudança de fase de 0,5 no gráfico da oscilação AB. Isso suporta a fase Berry é π e as oscilações AB observadas podem ser a característica de transporte da portadora do estado de superfície em nosso BiSbTe ₃ isolante topológico [45].

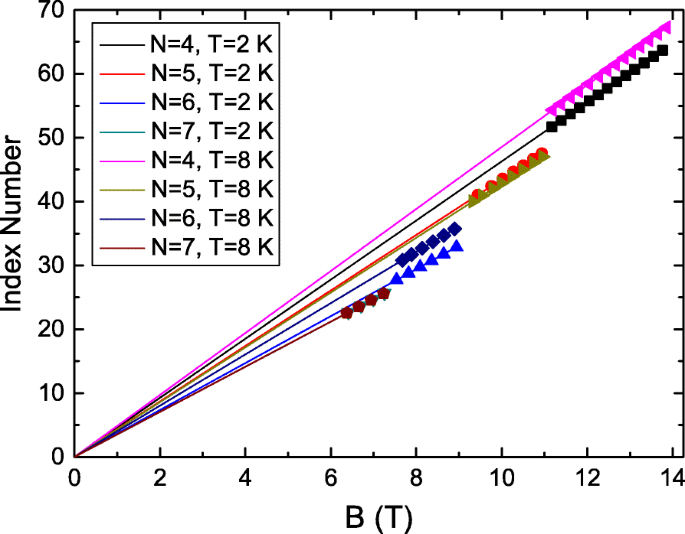
O número do índice de oscilação AB em função de B em diferentes níveis e temperaturas de Landau. A interceptação é de 0,25, o que indica uma mudança de fase de 0,5 no gráfico da oscilação AB. Isso suporta a fase Berry é π

Conclusão

Nós relatamos as oscilações quânticas em um BiSbTe ₃ macroflake isolante topológico. Além da oscilação Shubnikov-de Haas (SdH), ele revela oscilação semelhante a Aharonov-Bohm (ABL). O período de oscilação ABL é B -dependente. O período de oscilação ABL é constante em cada nível de Landau (LL). Os menores períodos de oscilação foram observados em LLs menores, o que foi determinado por meio da oscilação SdH. O período de oscilação é proporcional à raiz quadrada do LL em diferentes temperaturas. A proporção do período de oscilação ABL para a massa efetiva é uma dependência LL fraca. A oscilação ABL dependente de LL pode originar-se da massa efetiva dependente de LL.

Disponibilidade de dados e materiais

Os conjuntos de dados gerados durante e / ou analisados durante o estudo atual estão disponíveis nos autores correspondentes mediante solicitação razoável.

Abreviações

EDS:: Espectroscopia de raios-X de dispersão de energia
XPS:: espectroscopia de fotoelétrons de raios-X
ARPES:: Espectroscopia de fotoemissão de ângulo resolvido
SdH:: Shubnikov-de Haas

Um caminho rápido para filmes finos de óxido monocristalino autônomo usando YBa2Cu3O7-x como camada sacrificial Cinética e especificidade da captação de vesículas extracelulares HEK293T usando citometria de fluxo de imagem

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias