Estouro binário

Uma ressalva com os números binários com sinal é a do overflow, em que a resposta a um problema de adição ou subtração excede a magnitude que pode ser representada com o número de bits atribuído. Lembre-se de que o local do bit do sinal está fixo desde o início do problema.

Com o último exemplo de problema, usamos cinco bits binários para representar a magnitude do número, e o bit mais à esquerda (sexto) como o bit de peso negativo, ou sinal. Com cinco bits para representar a magnitude, temos um intervalo de representação de 2 ⁵ , ou trinta e duas etapas inteiras de 0 ao máximo.

Isso significa que podemos representar um número tão alto quanto +31 ₁₀ (011111 ₂ ), ou tão baixo quanto -32 ₁₀ (100.000 ₂ )

Restrições do campo numérico de seis bits

Se configurarmos um problema de adição com dois números binários, o sexto bit usado para sinal, e o resultado exceder +31 ₁₀ ou é menor que -32 ₁₀ , nossa resposta estará incorreta. Vamos tentar adicionar 17 ₁₀ e 19 ₁₀ para ver como essa condição de estouro funciona para números positivos excessivos:





A resposta (100100 ₂ ), interpretado com o sexto bit como -32 ₁₀ lugar, é na verdade igual a -28 ₁₀ , não +36 ₁₀ como devemos obter com +17 ₁₀ e +19 ₁₀ adicionados juntos! Obviamente, isso não é correto. O que deu errado?

A resposta está nas restrições do campo de número de seis bits dentro do qual estamos trabalhando. Desde a magnitude da soma verdadeira e apropriada (36 ₁₀ ) excede o limite permitido para nosso campo de bit designado, temos um erro de estouro .

Simplificando, seis casas não fornecem bits suficientes para representar a soma correta, então qualquer valor que obtivermos usando a estratégia de descartar o bit "carry" mais à esquerda estará incorreto.

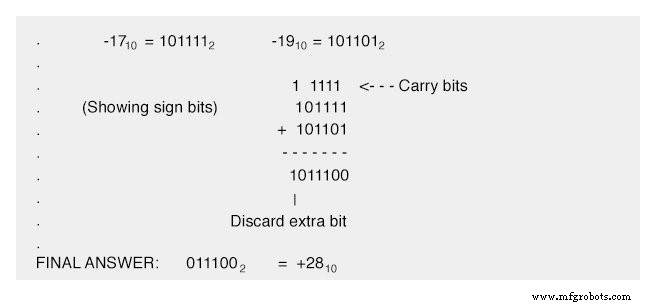
Um erro semelhante ocorrerá se somarmos dois números negativos para produzir uma soma muito baixa para nosso campo binário de seis bits. Vamos tentar adicionar -17 ₁₀ e -19 ₁₀ juntos para ver como isso funciona (ou não funciona, conforme o caso!):



A resposta (incorreta) é uma positiva vinte e oito. O fato de que a soma real de dezessete negativos e dezenove negativos era muito baixa para ser representada corretamente com um campo de magnitude de cinco bits e um sexto bit de sinal é a causa raiz desta dificuldade.

Usando o sétimo bit para um bit de sinal

Vamos tentar esses dois problemas novamente, exceto desta vez usando o sétimo bit para um bit de sinal e permitindo o uso de 6 bits para representar a magnitude:







Usando campos de bits suficientemente grandes para lidar com a magnitude das somas, chegamos às respostas corretas. Nestes problemas de amostra, fomos capazes de detectar erros de estouro realizando os problemas de adição na forma decimal e comparando os resultados com as respostas binárias.

Por exemplo, ao adicionar +17 ₁₀ e +19 ₁₀ juntos, sabíamos que a resposta era suposta para ser +36 ₁₀ , então quando a soma binária verificada for -28 ₁₀ , sabíamos que algo devia estar errado. Embora seja uma forma válida de detectar o estouro, não é muito eficiente.

Afinal, toda a ideia de complementação é ser capaz de somar números binários de forma confiável e não ter que verificar o resultado adicionando os mesmos números na forma decimal! Isso é especialmente verdadeiro para o propósito de construir circuitos eletrônicos para somar quantidades binárias:o circuito deve ser capaz de verificar se há estouro sem a supervisão de um ser humano que já sabe qual é a resposta correta.

O que precisamos é de um método simples de detecção de erros que não exija nenhuma aritmética adicional. Talvez a solução mais elegante seja verificar o sinal da soma e compare com os sinais dos números adicionados.

Obviamente, dois números positivos somados devem fornecer um resultado positivo e dois números negativos somados devem fornecer um resultado negativo. Observe que sempre que tivemos uma condição de estouro nos problemas de exemplo, o sinal da soma foi sempre oposto dos dois números adicionados:+17 ₁₀ mais +19 ₁₀ dando -28 ₁₀ , ou -17 ₁₀ mais -19 ₁₀ dando +28 ₁₀ .

Ao verificar apenas os sinais, podemos dizer que algo está errado. Mas e os casos em que um número positivo é adicionado a um número negativo? Qual deve ser o sinal da soma para ficar correta. Ou, mais precisamente, que sinal de soma necessariamente indicaria um erro de estouro?

A resposta para isso é igualmente elegante: nunca ser um erro de estouro quando dois números de sinais opostos são somados! A razão para isso é aparente quando a natureza do estouro é considerada. O estouro ocorre quando a magnitude de um número excede a faixa permitida pelo tamanho do campo de bits.

A soma de dois números com sinais idênticos pode muito bem exceder a faixa do campo de bits desses dois números e, portanto, neste caso, o estouro é uma possibilidade. No entanto, se um número positivo for adicionado a um número negativo, a soma será sempre mais próxima de zero do que qualquer um dos dois números adicionados:sua magnitude deve ser menor que a magnitude de qualquer um dos números originais e, portanto, o estouro é impossível.

Felizmente, essa técnica de detecção de estouro é facilmente implementada em circuitos eletrônicos e é um recurso padrão em circuitos de somadores digitais:um assunto para um capítulo posterior.



PLANILHAS RELACIONADAS:

• Planilha de matemática binária