Método atual de filial

A primeira e mais direta técnica de análise de rede é chamada de Branch Current Method . Neste método, assumimos as direções das correntes em uma rede e, em seguida, escrevemos equações que descrevem suas relações entre si por meio das Leis de Kirchhoff e de Ohm. Uma vez que temos uma equação para cada corrente desconhecida, podemos resolver as equações simultâneas e determinar todas as correntes e, portanto, todas as quedas de tensão na rede.

Resolvendo usando o método atual de filial

Vamos usar este circuito para ilustrar o método:

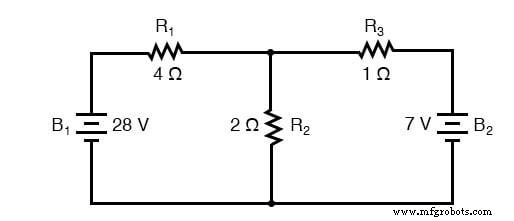
Escolha de um nó

O primeiro passo é escolher um nó (junção de fios) no circuito para usar como ponto de referência para nossas correntes desconhecidas. Vou escolher o nó à direita de R ₁ , o topo de R ₂ , e à esquerda de R ₃ .



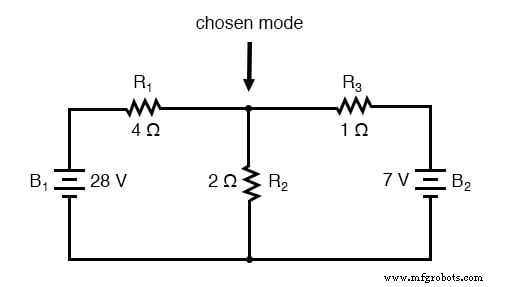
Neste nó, adivinhe quais direções as correntes dos três fios tomam, rotulando as três correntes como I ₁ , I ₂ e eu ₃ , respectivamente. Tenha em mente que essas direções da corrente são especulativas neste ponto. Felizmente, se descobrirmos que alguma de nossas suposições estava errada, saberemos quando resolvermos matematicamente as correntes (quaisquer direções de corrente “erradas” aparecerão como números negativos em nossa solução).

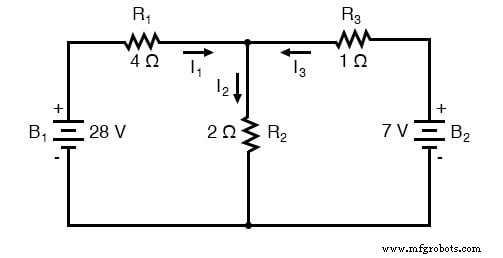
Aplicar a lei atual de Kirchhoff (KCL)

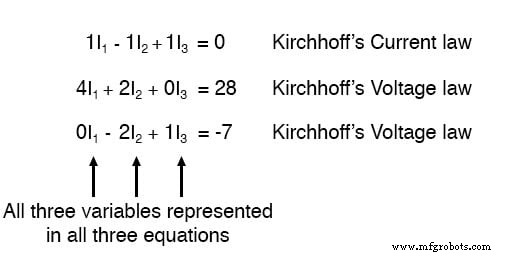
A Lei Atual de Kirchhoff (KCL) nos diz que a soma algébrica das correntes que entram e saem de um nó deve ser igual a zero, então podemos relacionar essas três correntes (I ₁ , I ₂ e eu ₃ ) entre si em uma única equação. Para fins de convenção, denotarei qualquer entrada atual o nó tem sinal positivo, e qualquer corrente saindo o nó como negativo em sinal:

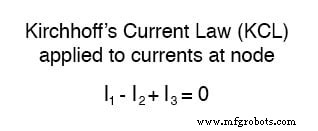
Identifique todas as quedas de tensão

A próxima etapa é rotular todas as polaridades de queda de tensão nos resistores de acordo com as direções assumidas das correntes. A polaridade é positiva onde a corrente entra no resistor e negativa onde sai do resistor:



As polaridades da bateria, é claro, permanecem como estavam de acordo com sua simbologia (extremidade curta negativa, extremidade longa positiva). Está tudo bem se a polaridade da queda de tensão de um resistor não corresponder à polaridade da bateria mais próxima, desde que a polaridade da tensão do resistor seja baseada corretamente na direção assumida da corrente através dele. Em alguns casos, podemos descobrir que a corrente será forçada para trás através de uma bateria, causando esse mesmo efeito. O importante a lembrar aqui é basear todas as polaridades do resistor e cálculos subsequentes nas direções da (s) corrente (s) inicialmente assumidas. Conforme declarado anteriormente, se sua suposição estiver incorreta, ela ficará aparente assim que as equações forem resolvidas (por meio de uma solução negativa). A magnitude da solução, no entanto, ainda estará correta.

Aplicar a lei de tensão de Kirchhoff (KVL)

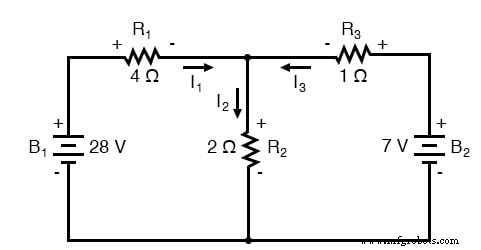
A Lei de Tensão de Kirchhoff (KVL) nos diz que a soma algébrica de todas as tensões em um loop deve ser igual a zero, então podemos criar mais equações com termos de corrente (I ₁ , I ₂ e eu ₃ ) para nossas equações simultâneas. Para obter uma equação KVL, devemos registrar as quedas de tensão em um loop do circuito, como se estivéssemos medindo com um voltímetro real. Vou escolher traçar o loop esquerdo deste circuito primeiro, começando do canto superior esquerdo e movendo no sentido anti-horário (a escolha de pontos de partida e direções é arbitrária). O resultado será assim:









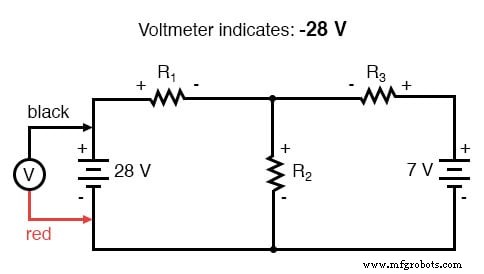
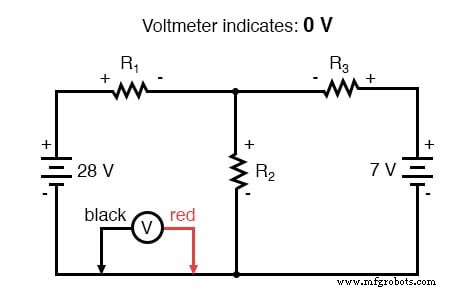
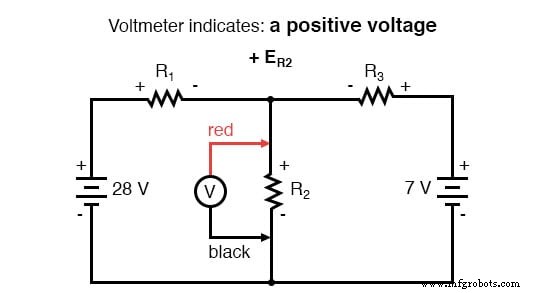
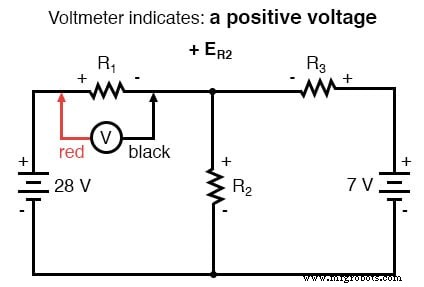
Tendo completado nosso traçado do loop esquerdo, adicionamos essas indicações de tensão juntas para uma soma de zero:



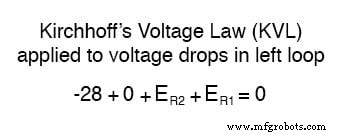
Claro, ainda não sabemos qual é a tensão em R ₁ ou R ₂ , portanto, não podemos inserir esses valores na equação como números numéricos neste ponto. No entanto, nós fazemos saiba que todas as três tensões devem somar algebricamente a zero, então a equação é verdadeira. Podemos dar um passo adiante e expressar as tensões desconhecidas como o produto das correntes desconhecidas correspondentes (I ₁ e eu ₂ ) e seus respectivos resistores, seguindo a Lei de Ohm (E =IR), bem como eliminar os termos 0:

Como sabemos quais são os valores de todos os resistores em ohms, podemos apenas substituir esses números na equação para simplificar um pouco as coisas:



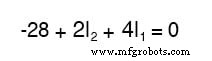
Você pode estar se perguntando por que tivemos todo o trabalho de manipular esta equação a partir de sua forma inicial (-28 + E _R2 + E _R1 ) Afinal, os dois últimos termos ainda são desconhecidos, então qual a vantagem de expressá-los em termos de tensões desconhecidas ou como correntes desconhecidas (multiplicadas por resistências)? O objetivo ao fazer isso é obter a equação KVL expressa usando as mesmas variáveis ​​desconhecidas como a equação KCL, pois este é um requisito necessário para qualquer método de solução de equação simultânea. Para resolver três correntes desconhecidas (I ₁ , I ₂ e eu ₃ ), devemos ter três equações relacionando essas três correntes (não tensões !) juntos.

Aplicando as mesmas etapas ao loop direito do circuito (começando no nó escolhido e movendo no sentido anti-horário), obtemos outra equação KVL:











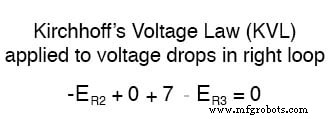
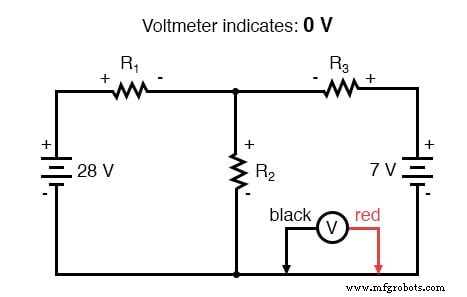
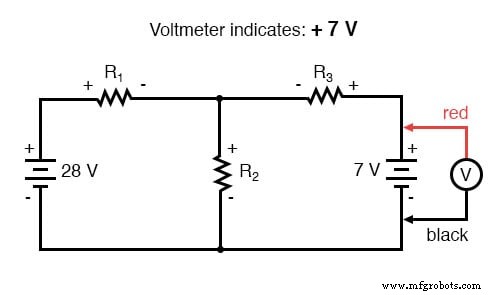
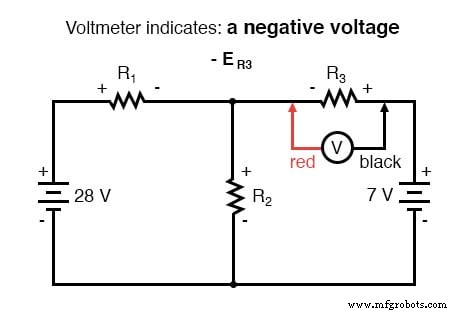
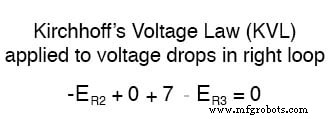
Sabendo agora que a tensão em cada resistor pode e deve ser expresso como o produto da corrente correspondente e a resistência (conhecida) de cada resistor, podemos reescrever a equação como tal:

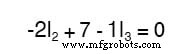
Resolvendo o desconhecido

Agora temos um sistema matemático de três equações (uma equação KCL e duas equações KVL) e três incógnitas:



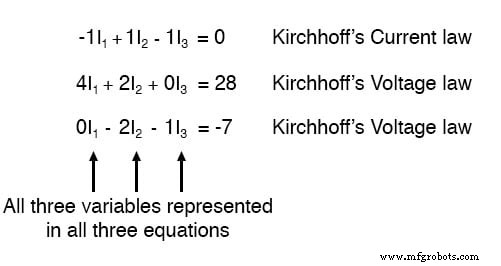
Para alguns métodos de solução (especialmente qualquer método envolvendo uma calculadora), é útil expressar cada termo desconhecido em cada equação, com qualquer valor constante à direita do sinal de igual e com quaisquer termos de “unidade” expressos com um coeficiente explícito de 1. Reescrevendo as equações novamente, temos:



Usando quaisquer técnicas de solução disponíveis para nós, devemos chegar a uma solução para os três valores atuais desconhecidos:



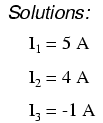
Então, eu ₁ é 5 amperes, eu ₂ é 4 amperes e eu ₃ é 1 ampere negativo. Mas o que significa corrente “negativa” significa? Neste caso, significa que nosso assumido direção para I ₃ era o oposto de seu real direção. Voltando ao nosso circuito original, podemos redesenhar a seta atual para I ₃ (e redesenhe a polaridade de R ₃ Queda de tensão para combinar):

Redesenhe o circuito

Observe como a corrente está sendo empurrada para trás através da bateria 2 (elétrons fluindo “para cima”) devido à tensão mais alta da bateria 1 (cuja corrente está apontada “para baixo” como faria normalmente)! Apesar do fato de que a polaridade da bateria B2 está tentando empurrar os elétrons para baixo nesse ramo do circuito, os elétrons estão sendo forçados de volta através dele devido à voltagem superior da bateria B1. Isso significa que a bateria mais forte sempre “vencerá” e a bateria mais fraca sempre terá a corrente forçada para trás? Não! Na verdade, depende das tensões relativas das baterias e os valores do resistor no circuito. A única maneira de determinar o que está acontecendo é reservar um tempo para analisar matematicamente a rede.

Calcule a queda de tensão em todos os resistores

Agora que sabemos a magnitude de todas as correntes neste circuito, podemos calcular as quedas de tensão em todos os resistores com a Lei de Ohm (E =IR):

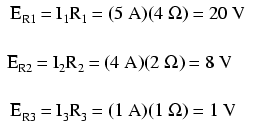
Analise a rede usando SPICE

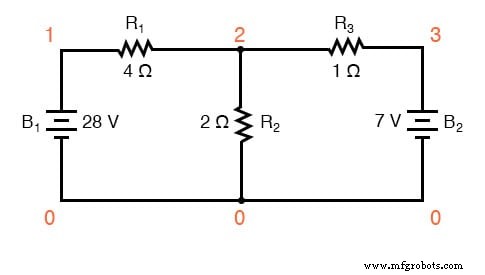
Vamos agora analisar esta rede usando SPICE para verificar nossos valores de tensão. Poderíamos analisar a corrente também com SPICE, mas como isso requer a inserção de componentes extras no circuito, e porque sabemos que se as tensões são todas iguais e todas as resistências são as mesmas, as correntes devem todos iguais, optarei pela análise menos complexa. Aqui está um redesenho do nosso circuito, completo com os números dos nós para que o SPICE faça referência:

 exemplo de análise de rede v1 1 0 v2 3 0 dc 7 r1 1 2 4 r2 2 0 2 r3 2 3 1 .dc v1 28 28 1 .print dc v (1,2) v (2,0) v (2,3) .fim v1 v (1,2) v (2) v (2,3) 2.800E + 01 2.000E + 01 8.000E + 00 1.000E + 00 

Com certeza, os valores de voltagem acabaram sendo todos iguais:20 volts em R ₁ (nós 1 e 2), 8 volts em R ₂ (nós 2 e 0), e 1 volt em R ₃ (nós 2 e 3). Observe os sinais de todos esses valores de tensão:todos são valores positivos! O SPICE baseia suas polaridades na ordem em que os nós são listados, o primeiro nó sendo positivo e o segundo nó negativo. Por exemplo, um valor positivo (+) 20 volts entre os nós 1 e 2 significa que o nó 1 é positivo em relação ao nó 2. Se o número tivesse saído negativo na análise SPICE, saberíamos que nossa polaridade real era “Para trás” (nó 1 negativo em relação ao nó 2). Verificando as ordens dos nós na lista SPICE, podemos ver que todas as polaridades correspondem ao que determinamos por meio do método de análise Branch Current.

REVER:

• Passos a seguir para o método de análise “Branch atual”:
  • Escolha um nó e assuma as direções das correntes.
  • Escreva uma equação KCL relacionando as correntes no nó.
  • Identifique as polaridades de queda de tensão do resistor com base nas correntes assumidas.
  • Escreva as equações KVL para cada loop do circuito, substituindo o produto IR por E em cada termo do resistor das equações.
  • Resolva para correntes de ramificação desconhecidas (equações simultâneas).
  • Se alguma solução for negativa, a direção assumida da corrente para essa solução está errada!
  • Resolva as quedas de tensão em todos os resistores (E =IR).

PLANILHA RELACIONADA:

• Planilha de análise de corrente da filial DC